- Учителю
- Урок по теме «Пропорциональное деление» (6 класс)
Урок по теме «Пропорциональное деление» (6 класс)
Пропорциональное деление
-
Сережа собрал 2,4 кг клубники. Четыре части он отдал сестре Наташе, три части - брату Коле, а одну часть оставил себе. Сколько килограммов клубники получил каждый?
Решение: х кг - масса одной части
Сережа - х кг, Наташа - 4х кг, Коля - 3х кг
х + 4х + 3х = 2,4
х = 0,3
Сережа - 0,3 кг, Наташа - 1,2 кг, Коля - 0,9 кг
-
Для приготовления компота требуется вода, ягоды и сахар, массы которых должны быть пропорциональны числам 4, 3 и 2 соответственно. Сколько надо взять воды, ягод и сахара (по массе) для приготовления 13,5 кг компота?
Решение: пусть х - коэффициент пропорциональности.
Тогда масса воды - 4х кг, масса ягод - 3х кг, сахара - 2х кг.
4х + 3х + 2х = 13,5
9х = 13,5
х = 1,5
Масса воды - 6 кг, масса ягод - 4,5 кг, сахара - 3 кг.
-
Отрезок длиной 1 м разделили на две части, длины которых пропорциональны числам 2 и 3. Найдите длины этих отрезков.
Решение: 1 способ. Пусть х - коэффициент пропорциональности. Тогда длина первого отрезка 2х м, длина второго - 3х м.
2х + 3х = 1
х = 0,2
длины отрезков 0,4 м и 0,6 м
2 способ. Найдем длину одной части 2+3=5 частей
1:5=0,2 м - длина одной части
-
Число 88 разделите на три части пропорционально числам
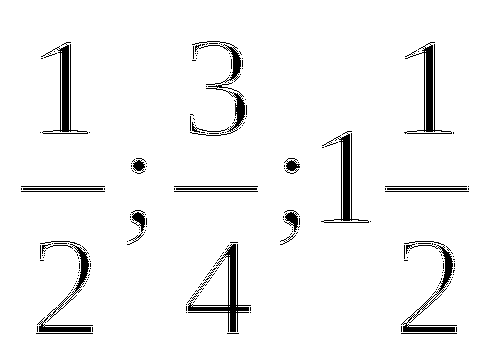 .
.
Решение: Пусть х - коэффициент пропорциональности.
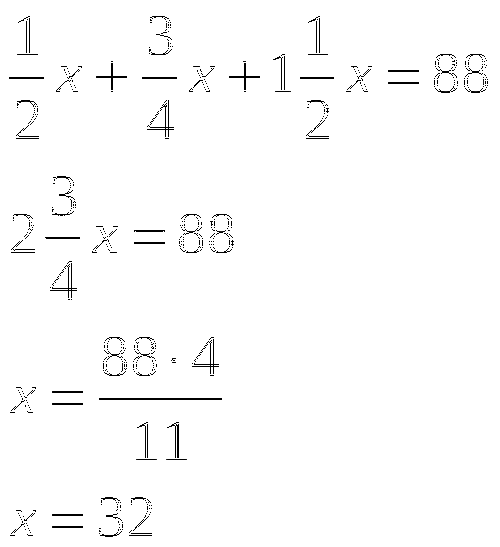
88=16+24+48
-
Три числа относятся, как 3:5:8, третье число равно 112. Вычислите два первых числа.
Решение: Пусть х - коэффициент пропорциональности.
8х = 112
х = 14 - коэффициент пропорциональности
первое число - 42, второе - 70
-
Отношение двух чисел равно отношению
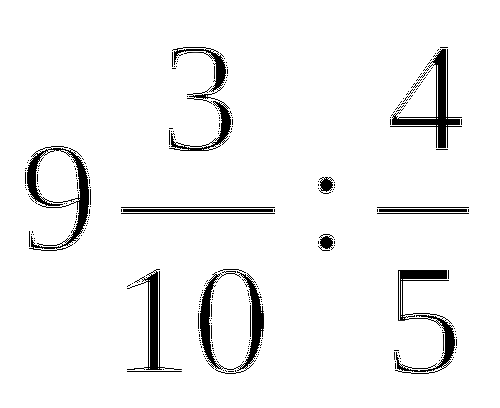 . Одно число больше другого на 34. Найдите эти числа.
. Одно число больше другого на 34. Найдите эти числа.
Решение: Пусть х - коэффициент пропорциональности.
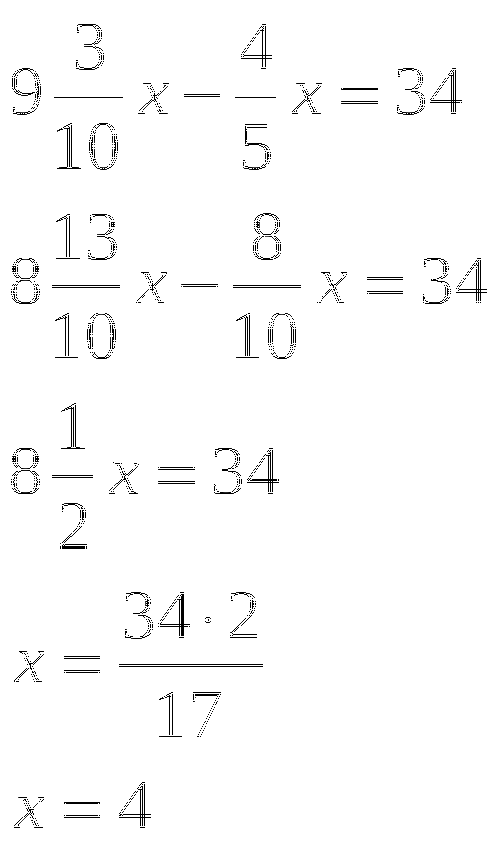
Первое число - ![]() , второе -
, второе - ![]() .
.
-
Найдите три числа, если известно, что первое из них относится к третьему, как
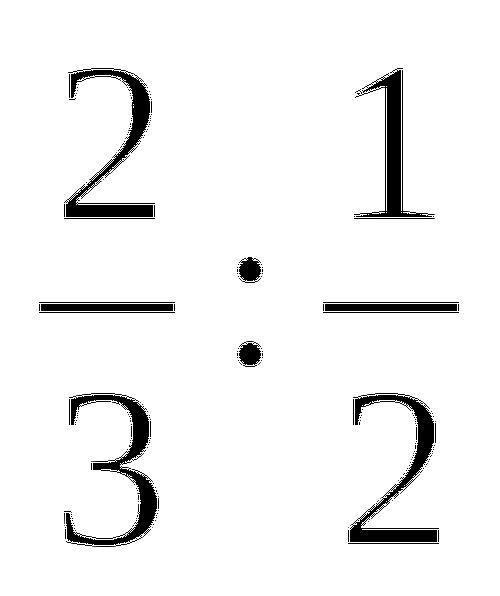 , а третье число относится ко второму, как
, а третье число относится ко второму, как 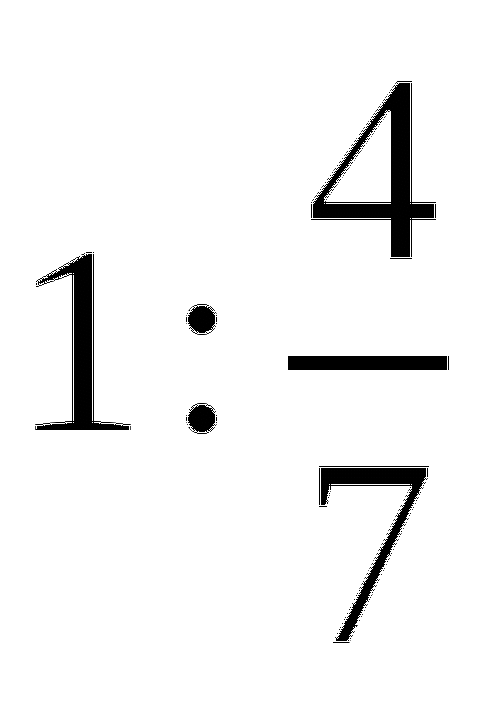 , и что второе число в сумме с третьим составляет 60.
, и что второе число в сумме с третьим составляет 60.
Решение: Пусть х - коэффициент пропорциональности.
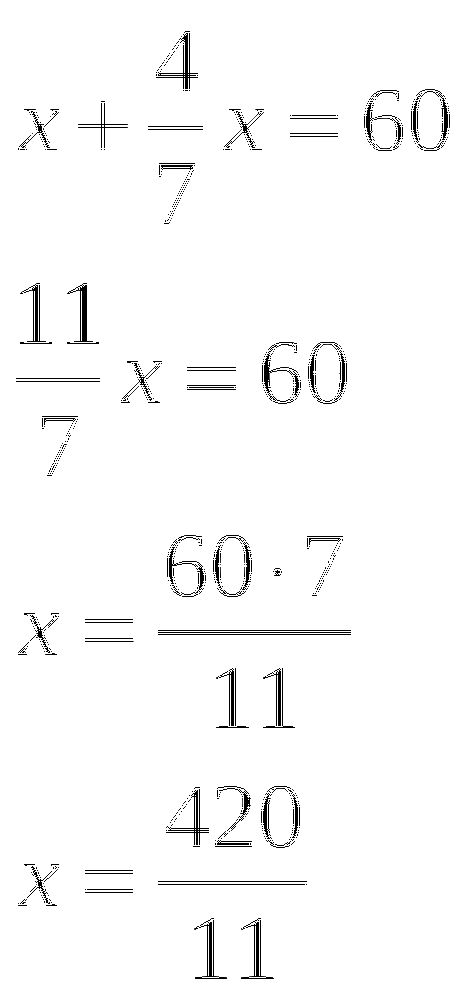
Третье число - ![]() , второе число -
, второе число - ![]() .
.
Пусть у - коэффициент пропорциональности.
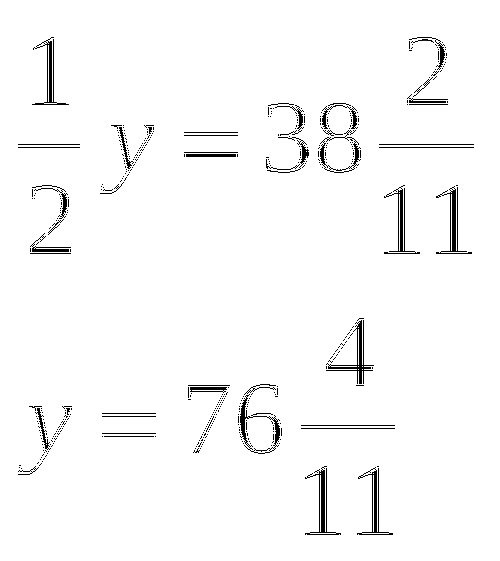
Первое число - ![]() .
.
-
Собственная скорость парохода относится к скорости течения реки, как 36:5. Пароход двигался вниз по течению реки 5 ч 10 мин. Сколько времени потребуется ему, чтобы вернуться обратно?
Решение: Пусть х - коэффициент пропорциональности.
Тогда собственная скорость парохода - 36х км/ч, скорость течения - 5х км/ч, скорость против течения - 31х км/ч, скорость по течению - 41х км/ч.
Скорость по течению относится к скорости против течения, как 41:31.
-
Скорость
Время
4
 1
1 5
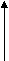 ч 10 мин =
ч 10 мин =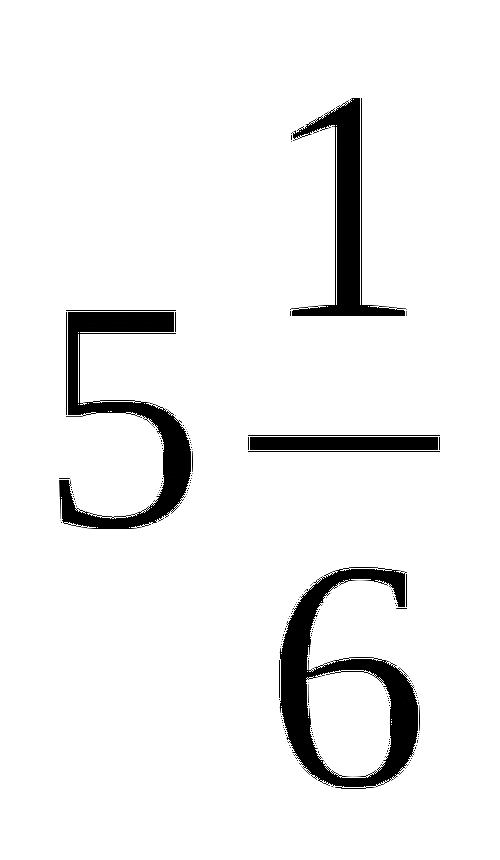 ч
ч 31
х ч
Обратная пропорциональность
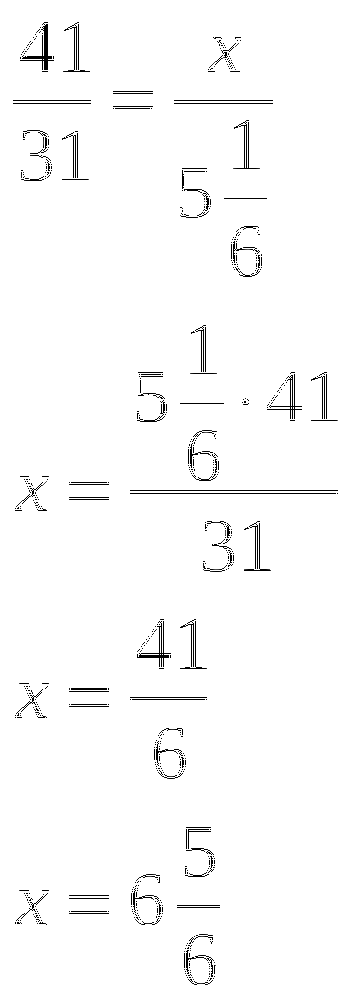
![]() - время на обратный путь
- время на обратный путь
-
Разделите число 144 на три части х, у, z так, чтобы х:у=3:4, у:z=4:5.
Решение: х:у:z=3:4:5
Всего 3+4+5=12 частей
144:12=12 - одна часть
х=36, у=48, z=60.
-
Разделите число 310 на три части х, у, z так, чтобы х:у=3:2, у:z=5:3.
Решение:
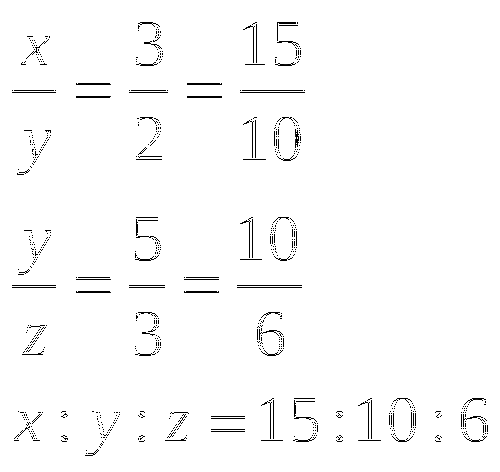
Всего 15+10+6=31 часть
310:31=10 - одна часть
х=150, у=100, z=60.
-
Сумма трех чисел равна 90. Произведения первого числа на 10, второго числа на 15 и третьего числа на 5 равны между собой. Найдите эти числа.
Решение: пусть х, у, z - данные числа.
10x=15y, 15y=5z
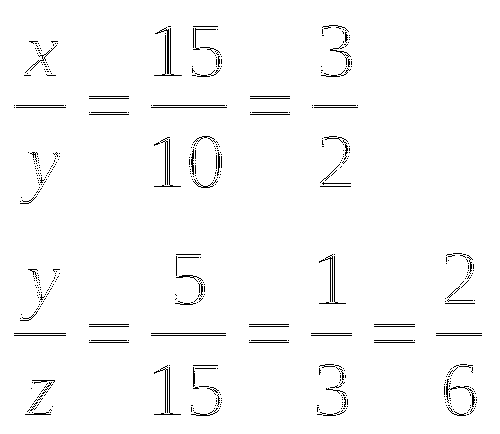
![]()
Всего 3+2+6=11 частей
![]()
Первое число - ![]() , второе -
, второе - ![]() , третье -
, третье - ![]() .
.
-
От станции до поселка 4 км. Турист решил это расстояние разделить на три части, пропорциональные числам т, 2т, т-3. Найдите, сколько километров составляет каждая часть пути. При любом ли значении т можно решить эту задачу?
Решение: всего т + 2т + т-3 = 4т - 3 частей
Найдем длину одной части: ![]()
Длина первой части - ![]() км, длина второй части -
км, длина второй части - ![]() км, длина третьей части -
км, длина третьей части - ![]() км.
км.
Задача имеет решение при ![]()
Пропорциональное деление
-
Сережа собрал 2,4 кг клубники. Четыре части он отдал сестре Наташе, три части - брату Коле, а одну часть оставил себе. Сколько килограммов клубники получил каждый?
-
Для приготовления компота требуется вода, ягоды и сахар, массы которых должны быть пропорциональны числам 4, 3 и 2 соответственно. Сколько надо взять воды, ягод и сахара (по массе) для приготовления 13,5 кг компота?
-
Отрезок длиной 1 м разделили на две части, длины которых пропорциональны числам 2 и 3. Найдите длины этих отрезков.
-
Число 88 разделите на три части пропорционально числам
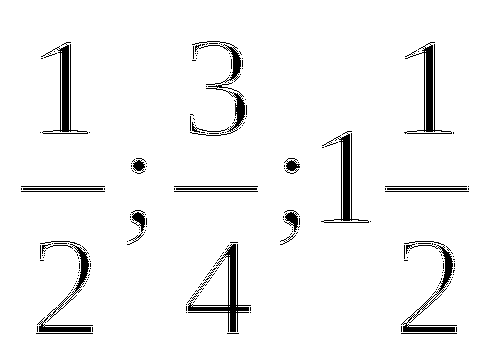 .
.
-
Три числа относятся, как 3:5:8, третье число равно 112. Вычислите два первых числа.
-
Отношение двух чисел равно отношению
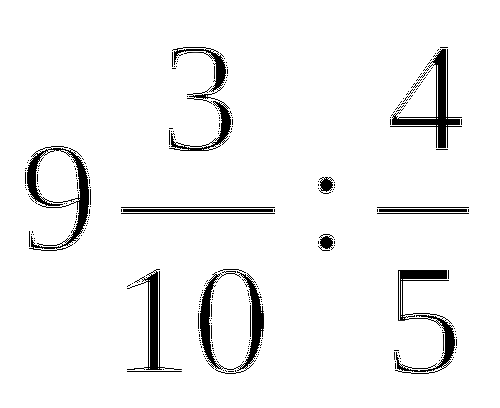 . Одно число больше другого на 34. Найдите эти числа.
. Одно число больше другого на 34. Найдите эти числа.
-
Найдите три числа, если известно, что первое из них относится к третьему, как
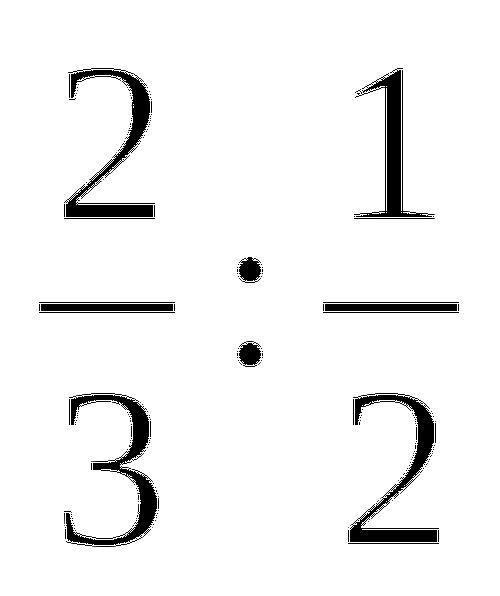 , а третье число относится ко второму, как
, а третье число относится ко второму, как 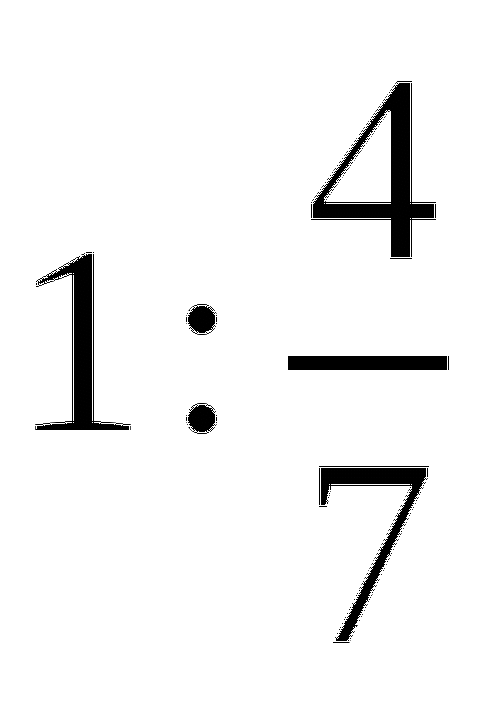 , и что второе число в сумме с третьим составляет 60.
, и что второе число в сумме с третьим составляет 60.
-
Собственная скорость парохода относится к скорости течения реки, как 36:5. Пароход двигался вниз по течению реки 5 ч 10 мин. Сколько времени потребуется ему, чтобы вернуться обратно?
-
Разделите число 144 на три части х, у, z так, чтобы х:у=3:4, у:z=4:5.
-
Разделите число 310 на три части х, у, z так, чтобы х:у=3:2, у:z=5:3.
-
Сумма трех чисел равна 90. Произведения первого числа на 10, второго числа на 15 и третьего числа на 5 равны между собой. Найдите эти числа.
-
От станции до поселка 4 км. Турист решил это расстояние разделить на три части, пропорциональные числам т, 2т, т-3. Найдите, сколько километров составляет каждая часть пути. При любом ли значении т можно решить эту задачу?