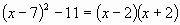Урок по алгебре для 7 класса «Формулы сокращённого умножения»

Областная специализированная школа для одарённых детей №8.

Тема урока: «Формулы сокращенного умножения».

7 класс

Учитель математики второй категории

Шикова Л.К.

2013-2014 учебный год.

Дидактическая цель: создание условий для закрепления и систематизации знаний по теме, закрепление общеучебных умений и навыков.

Цели по содержанию:
1. Образовательная: систематизировать знания учащихся по теме, закрепить умение применять их, определить степень усвоения материала, знать формулы сокращенного умножения.
2. Развивающая: уметь применять формулы сокращенного умножения на практике, развивать вычислительные навыки, логическое мышление.
3. Воспитательная: продолжить воспитание математической культуры учащихся, стимулировать развитие интереса к данной теме и к дисциплине в целом; продолжить воспитание ответственности, аккуратности при выполнении различных заданий, настойчивости при достижении цели.

Задачи урока:

-создать положительную психологическую атмосферу для максимального раскрытия их способностей в игре;

-развивать умение формулировать и высказывать свои мысли, применять знания на практике;

-развивать познавательные процессы, память, внимание, наблюдательность, сообразительность.

Тип урока: закрепление и систематизация знаний.

Методы: словесный, объяснительно-иллюстративный.

Формы организации деятельности учащихся: индивидуальная, работа в парах, групповая.

Оборудование: компьютер, мультимедийный проектор, экран, презентация, раздаточный материал, доска, мел.

План урока:

1. Организационный момент

2. Актуализация знаний

3. Контроль знаний

4. Итог урока. Рефлексия

Ход урока

I. Организационный момент. Сообщение темы, цели урока.

Французский писатель 19 столетия Анатоль Франс однажды заметил: "Учиться можно только весело. Чтобы переваривать знания, надо поглощать их с аппетитом". Так вот, давайте сегодня на уроке будем следовать этому совету писателя, будем активны, будем, логически мыслить и закрепим знания по теме.

Сегодня на уроке стоит задача - показать, как вы знаете формулы сокращенного умножения, как умеете применять их при разложении многочлена на множители, а также для вычислений значений выражений наиболее рациональным способом.

Урок будет проходить под девизом:

«Дорогу осилит идущий, а математику - мыслящий».

Прежде, чем приступить к работе, каждый из вас должен поставить перед собой цель сегодняшнего урока. Перед вами лежат оценочные листы, в левом столбце написаны цели, выберите те, которые соответствуют вашим, и поставьте напротив знак «+» или допишите свою. На каждом этапе урока вы будете оценивать себя или своих товарищей, выставляя количество заработанных баллов в оценочные листы. Сегодня на уроке вы поработаете в парах, в группах.

Сначала мы повторим пройденное.

II. Актуализация знаний.

1. Проверка знаний:

А) Понимание математической речи на слух. (5 мин)

На доске выписаны формулы, у каждой свой номер. Называю левую или правую часть, вы записываете номер этой формулы. В конце получится число, его и проверим.

1) а³ + в³ = (а + в) (а² - ав + в²)

2) (а - в)² = а² - 2ав +в²

3) (а - в) (а + в) = а² - в²

4) а³ - в³ = (а - в)(а² + ав + в²)

5) (а + в)² = а² + 2ав + в²

• Квадрат разности двух выражений.

• Разность квадратов двух выражений.

• Сумма кубов двух выражений.

• Квадрат первого выражения плюс удвоенное произведение первого и второго выражений плюс квадрат второго выражения.

• Произведение разности двух выражений и их суммы.

• Разность кубов двух выражений.

Ответ: 2 3 1 5 3 4.

Оцените себя (6 баллов).

Б) Задание с выбором ответа. (7 мин)

Двое учеников выполняют задание на магнитной доске. Остальные работают в парах. Соединить линиями части верного равенства. Но для двух выражений ответов нет, их нужно решить самим. За каждый верный ответ 1 балл, за верно решенный пример - 2 балла. Всего - 10 баллов.

Ответ: (у² + 2х³)² = у⁴ + 4х³у + 4х⁶; (4у - 1)(4у +1) = 16у² - 1.

В). Работа в парах. (5 мин)

Каждый ученик работает с заданием по карточке, а затем сверяют ответы с соседом по парте. А затем проверяют решение по ответнику. За каждое верно выполненное задание начисляется 1 балл.

1) Представьте в виде многочлена:

а) (а - 5)²;
б) (х + 4)²;
в) (- 5 + х)²;
г) (0,1х - 3)(0,1х + 3);
д) (0,1у - 0,5)²;
е) (- а - 5)².

2) Вычислите:

а) 14² - 13²;
б)15² + 11².

3) Сократить дробь .

Образец выполнения работы:

а) (а - 5)² = а² - 10а + 25;
б) (х + 4)² = х² + 8х + 16;
в) (- 5 + х)² = 25 - 10х + х²;
г) (0,1х - 3)(0,1х + 3) = 0,01х² - 9;
д) (0,1у - 0,5)² = 0,01у² - 0,1у + 0,25;
е) (- а - 5)² = а² + 10а + 25.

2) Вычислите:

а) 14² - 13² = (14 - 13)(14 + 13) = 27; б)15² + 11² = 225 + 121 = 346.

3) Сократить дробь = = = .

Г) Фронтальная работа на отработку навыков применения формул сокращенного умножения

1. Для чего же нужно знать формулы сокращенного умножения? Где они применяются? Сейчас вы, выполняя следующие задания объясните, где и какие формулы вы использовали.

Работа по учебнику: № 187 (1,3)

№ 190

Задача. Как изменится площадь квадрата, если одну из смежных сторон увеличить на 4, а другую уменьшить на 4?

III Контроль знаний

Учащиеся выполняют тест, ответы записывают на листочках и сдают учителю (10 мин). Оценка 6 баллов.

Тест

6. Даны равенства:

Домашнее задание: ____________________

Работа в группах: 3 группы выполняют задание на плакатах

Известно, что а+в= - 10, а - в = 1,1.

Найдите значение выражений: 1) a² + 2ab + b²

2) a² - 2ab + b²

3) a² - 2ab + b² + 1,2

4) a² + 2ab + b² - а - в

5)1 - a² - 2ab - b²

6)2 a² + 2 b²

IV. Подведение итогов, рефлексия

Рефлексия деятельности (итог урока)

- Что делали сегодня на уроке?
- Что исправили?
- Над чем надо еще поработать?
- Оцените свою работу? Итак, возьмите свои оценочные листы, подсчитайте количество заработанных баллов, поставьте себе оценку.

• Если вы набрали 30 баллов и более - оценка "5",

• 22 - 29 баллов - оценка "4",

• 16 - 21 балл - оценка "3".

Оцените степень усвоенности материала

- Что необходимо повторить для, успешной работы, на последующих уроках?

Дополнительное задание:

I вариант

(x-2)² = x²- 4x-4

(2x+3y)² = 4x²+12xy+6y²

(a+2b)(a-2b) = a²- 4b²

II вариант

(x+3)² = x² -6x+9

(4x-2y)² = 16x²-16xy+4y

4a²-b²=(2a-b)(2a+b)

Дополнительное задание:

I вариант

(x-2)² = x²- 4x-4

(2x+3y)² = 4x²+12xy+6y²

(a+2b)(a-2b) = a²- 4b²

II вариант

(x+3)² = x² -6x+9

(4x-2y)² = 16x²-16xy+4y

4a²-b²=(2a-b)(2a+b)

Правильные ответы

I вариант

(x-2)² = x²- 4x+4

(2x+3y)² = 4x²+12xy+9y²

(a+2b)(a-2b) = a²- 4b²

II вариант

(x+3)² = x² -6x+9

(4x-2y)² = 16x²-16xy+4y²

4a²-b²=(2a-b)(2a+b)

Правильные ответы

I вариант

(x-2)² = x²- 4x+4

(2x+3y)² = 4x²+12xy+9y²

(a+2b)(a-2b) = a²- 4b²

II вариант

(x+3)² = x² -6x+9

(4x-2y)² = 16x²-16xy+4y²

4a²-b²=(2a-b)(2a+b)

Сначала мы повторим некоторые понятия:

Выражение, представляющее собой сумму одночленов - многочлен.

Выражение 2x²y⁴x - одночлен в стандартном виде.

Одночлены с одинаковой буквенной частью - подобные члены.

Квадрат двучлена (a - 2b) равен a² - 2ab + 4b².

Выражение (x² + y²) представляет собой квадрат суммы.

.

VII.Итог урока. Вопросы.1.Какие интересные места мы посетили на уроке? 2.Где вам понравилось больше всего? 3.Какие типы заданий делали? 4.Что вызвало наибольшее затруднение?

Сегодня, выполняя разнообразные задания, вы иногда допускали ошибки И это не удивительно, любой человек не застрахован от ошибок. Важно вовремя найти и исправить эти ошибки, понять, почему они появились, и стараться впредь их не допускать.

VIII.Домашнее задание

Что в переводе с древнеарабского означает слово "АЛГЕБРАИСТ?" (Костоправ) Благодарю вас за сотрудничество, взаимопонимание и просто за приятное совместное путешествие.Успехов вам в учебе. Урок окончен.

Решите уравнение:

Решение:

;