Урок алгебры в 7 классе по теме «Путешествие в страну Степени»

Урок алгебры в 7 классе по теме

«Путешествие в страну Степени» Слайд 1.

Тип урока: обобщающий.

Цели урока:

• проверить в игровой форме теоретические и практические знания по теме «Степень»;

• активизировать мыслительную деятельность учащихся посредством участия каждого из них в игре;

• развитие математического кругозора, речи, внимания;

• развитие информационных и коммуникативных компетенций.

Методы обучения: словесный, наглядный, практический.

Оборудование: Урок проводится в классе, где имеется компьютер и проектор, т.к. основным дидактическим обеспечением урока является презентация, специально разработанная для этого урока.

Вступительное слово:

Девиз: «Кто хочет ограничиться настоящим без знания прошлого, тот никогда его не поймёт» (Г. В. Лейбниц) Слайд 2.

Сегодня мы отправимся в математическое путешествие в страну «Степени». Путешествие будет весёлым, интересным. Вам придётся немного подумать над теми заданиями, которые приготовили для вас на каждой остановке. Не сбиться с дороги и сделать все наши остановки нам поможет карта нашего путешествия, а также вам потребуются смекалка, сообразительность, внимание.

Итак - в путь! Слайд 3.

Рис.1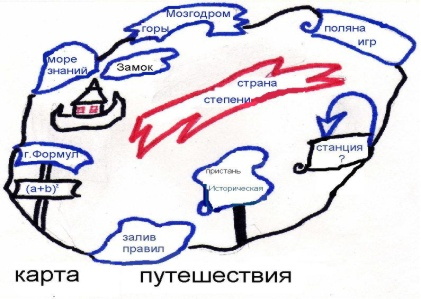

I. Пристань «Историческая».

В стране «Степеней» мы посетим пристань «Историческая», где узнаем много интересного и полезного из истории степеней.

Рассказы учеников о степени.

Презентация о степени Романовой Татьяны

«Картина «Устный счёт». Слайд 4.

Каждый из вас видел репродукцию с талантливой картины художника Богданова-Бельского «Устный счёт в народной школе Сергея Александровича Рачинского»

Рис.2

Сергей Александрович был одним из выдающихся профессоров Московского университета. Его глубоко волновала тяжёлая судьба русского крестьянина. В 1875 году учёный едет в село Татево Смоленской губернии и открывает народную школу, в которой обучает крестьянских детей. В своей работе Сергей Александрович уделяет внимание устному счёту. В картине «Устный счёт» художник хорошо передал урок математики своего учителя. На доске пример. Решите его устно.

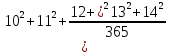= 2

II. Залив «Правил »

И вот залив «Правил». Давайте проверим, как мы знаем правила.

Теоретический конкурс.

Игра «Брейн - ринг» Слайд 5.

Дайте определение степени.

Как выполнить умножение степеней с одинаковым основанием?

Что называют возведением в степень?

Как возвести в степень произведение?

Как возвести в степень дробь?

Чему равна степень a с показателем 0? 1?

Чему равен угол в квадрате?

Как называют вторую степень?

III. Город формул Слайд 6.

Путешествие продолжается. Мы посетим город Формул, где нас ожидают интересные задания.

Используя равенство I. (10n+5)²=n(n+1)*100+25, вычислите

а) 85²=(10*8+5)²=8*(8+1)*100+25=7225

б) 995²=(10*99+5)²=99*(99+1)*100+25=990025

II.a²=(a+b)(a-b)+b² 63²=(63+3)(63-3)+3² = 3969

III. (a+b)(a-b)=a²-b² 71*69=(70+1)(70-1)=70²-1=4900-1=4899

IV Волшебный замок Слайд 7.

Отправляемся дальше. Вот перед нами замок. Он не простой - волшебный. Вам предстоит заполнить волшебный квадрат.

Впишите в клетки квадрата такие степени числа х, чтобы произведение их по любой горизонтали, вертикали, диагонали было равно х¹²:

Х²

Х³

Х⁴

Рис.3

Этот квадрат «пришёл к нам» из глубины веков. Его составили жрецы и назвали магическим. Верили, что такие квадраты придавали человеку необычные способности.

V Море знаний

Чтобы прибыть на следующую остановку, мы должны проплыть «Море знаний». Здесь мы должны выполнить тестовое задание. Учащиеся выполняют задания выбирая правильный ответ под определённой буквой и отгадывают слово.

Игра «Определи знак» Слайд 8.

Сравнить:

1

Е>

С=

У<

2

А<

С=

П>

3

П<

Х>

С=

4

А=

Е>

П<

5

П<

С=

Х>

1. (-11)^-7 11⁷ 4 .1² и 0,8²

2. (-16)⁸ и 16⁸ 5. 10²⁰ и 20¹⁰

3 .2*3² и 3*2³ Рис.5

Ответ: (успех)

VI. Горы «Мозгодром» Слайд 9.

Мы приближаемся к горам. Но чтобы их посетить, нужно исправить ошибки в вычислениях, проверить равенства.

Задание: «Где ошибка?» Выполняя задания на преобразование выражений, содержащих степени, ученик допустил ошибки:

1. 5*5*5*5=4⁵ 4. 2³+2⁷=2¹⁰ 5. 7¹=1

2.2³*2⁷=4¹⁰ 3.2³⁰/2¹⁰=2³ 6. (2х)³=2х³

Какие определения, свойства, правила не знает ученик?

«Верно ли равенство?» 12¹⁸=27⁶*16⁹ (Верно.)

VII. Поляна игр Слайд 10.

На этой станции проведём игру «Узнай слово!» Решив примеры, вы должны узнать учёного, который ввёл запись степеней.

1. (17²-15²):32=2 (д) 4. (3²¹+3²¹+3²¹) : 3¹⁸=81(а)

2. (2⁴*(2³)⁵): 2¹³=64 (е) 5. Х⁵=243 х=3(р)

3. 5²⁰: (5²)⁵: 5⁷: 5⁰=125(к) 6. 2^х=512 (т) Рис.6

Ответ: Декарт

VIII «Угадай - кА » Слайд 11.

А теперь отправляемся на конечную остановку - «Угадай- кА». Уже из названия станции вы узнали, что нам нужно что-то угадывать.

1.Удивительные степени: а) 1³³³=1 б) (((2)²)²)² =((4)²)²=(16)²=256

2.Угадай корень!

а) 2^х-5=2; б)2^х=512 ; в) х⁵=243: г) х³=(-8).

Вот и подошло к концу путешествие. Вам, ребята, спасибо за активное участие. Слайд 12.