- Учителю
- Разработка урока по алгебре 'Определение арифметической прогрессии' (9 класс)
Разработка урока по алгебре 'Определение арифметической прогрессии' (9 класс)
Муниципальное бюджетное образовательное учреждение
«Средняя общеобразовательная школа №14»
Конспект урока по алгебре
в 9 классе
«ОПРЕДЕЛЕНИЕ АРИФМЕТИЧЕСКОЙ ПРОГРЕССИИ»
подготовила Вакалова Н.Н.,
учитель математики
высшей категории
НИЖНЕВАРТОВСК
2015
Определение Арифметической прогрессии
Цели:
-повторение ранее изученного материала;
-определение арифметической прогрессии; формула n-го члена арифметической прогрессии;
-овладение знаниями и умениями, необходимыми для применения в практической деятельности;
-развитие умственных операций (перенос знаний, сравнение, анализ); вычислительных навыков;
-воспитание аккуратности, дисциплины; внимания, самоконтроля, интереса к предмету.
Ход урока
1. Организационный момент
2. Проверка домашнего задания
Через документ камеру проверить решение
3. Самостоятельная работа


4. Изложение нового материала (лекция)
Слайд 2
Определение. Числовую последовательность, каждый член которой, начиная со второго, равен сумме предыдущего члена и одного и того же числа d, называют арифметической прогрессией. Обозначение арифметической прогрессии
÷(ап): а1, а2, а3, ..., аn, ... .
При этом число d называют разностью прогрессии.
Таким образом, арифметическая прогрессия - это числовая последовательность (аn), заданная рекуррентно соотношениями:
а1 = а, an = an-1 + d (n = 2, 3, 4, ...) (a и d - заданные числа).
Слайд 3

Арифметическая прогрессия является
возрастающей последовательностью, если d > 0, и убывающей, если d < 0.
Слайд 4

Слайд 5

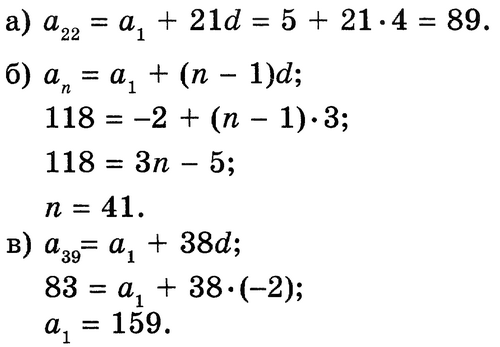
Слайд 6
№ 16.1
Ответы:
а)да; б)да;
в)да; г)нет.
№ 16.2
Ответы:
а)да; б)нет;
в)нет; г)нет.
5. Тренировочные упражнения
№ 16.3
d = a2 - a1 = a3 - a2 = a4 - a3 = …
а) а1=3; d=-4; б) а1=7; d=-3; в) а1=0,7; d=0,2;
№ 16.4 (в; г)
в) а1=-21; d=3; -21; -18; -15; -12; -9; -6.
г) а1=-17,5; d=-0,5; -17,5; -18; -19; -19,5; -20.
№ 16.5 (в; г)
в) а1=2; d=3; n=6; 2; 5; 8; 11; 14; 17.
г) а1=-6; d=1,5; n=4; -6; -4,5; -3; -1,5.
№ 16.7 (в; г)
в) 100; 90; 80; 70; … Найти d и а10.
а1 = 100; а2 = 90; d = а2 - а1 = 90 - 100 = -10; d = -10;
а10 = а1 + 9d = 100 + 9 (-10) = 100 - 90 = 10; а10 = 10.
Ответ: а10 = 10; d = -10.
г) 3; ![]()
![]()
![]() … Найти d и а10.
… Найти d и а10.
![]()
Ответ:а10=![]() ; d=
; d=![]() .
.
№ 16.11 (в; г) с комментированием на месте
в) хn=n2; нет;
г) хn=4n-3; х1=1; х2=5; х3=9; d=4; да.
№ 16.12 (в; г) самостоятельно
в) аn=-3n+1; а1=-2; а2=-5; а3=-8; d=-3; да;
г) аn=4n-3; х1=1; х2=5; х3=9; d=4; да.
Фронтальный опрос учащихся
- Какая последовательность называется арифметической прогрессией?
- Что такое разность арифметической прогрессии?
Итог урока
Домашнее задание:
§16. № 16.3 - 16.5(а,б); № 16.7(а,б); № 16.11 - 16.12(а,б).
Информационные источники
-
Мордкович А.Г., Семёнов П.В. Алгебра-9. Часть 1. Учебник.
2. Мордкович А.Г. , Мишустина Т.В., Тульчинская Е.Е., Семёнов П.В. Алгебра-9.
Часть 2. Задачник.
3. Александрова Л.А. Алгебра - 9. Самостоятельные работы / Под редакцией А.Г.Мордковича.