- Учителю
- Разработка урока по теме Градусная мера дуги окружности. Теорема о вписанном угле
Разработка урока по теме Градусная мера дуги окружности. Теорема о вписанном угле
Урок № 53
</ Тема: «Градусная мера дуги окружности. Теорема о вписанном угле».
Цель:
-
Способствовать применению учащимися полученных знаний при решении задач;
-
Ввести понятие вписанный угол;
-
Доказать теорему об измерении вписанных углов и следствие из нее
-
Подготовка к ГИА;
-
Развивать память, внимание и логическое мышление у обучающихся;
-
Вырабатывать трудолюбие, целеустремленность, умение работать в парах.
План урока.
-
Организационные моменты.
Сообщение темы и целей урока.
-
Актуализация знаний и умений обучающихся.
-
Проверка выполнения домашнего задания. (Разбор нерешенных заданий)
-
Проверка знания теоретического материала: Привести доказательства признака касательной к окружности.Заслушать одного ученика.
-
Решение задач.
1. Две окружности разных радиусов внешне
касаются. Докажите, что отрезок их общей касательной, заключенный
между точками касания, есть среднее пропорциональное между
диаметрами этих окружностей.ДОО1С, ![]() С = 90°
С = 90°
ОО1 = R + r
CО = R - r
![]()
![]() =
(r + R)2 - (R - r)2 =
=
(r + R)2 - (R - r)2 =
= r2 + 2rR + R2 - R2 + 2rR -
r2.
![]()
![]() .
.
2. Через концы диаметра АВ окружности проведены две касательные к ней. Третья касательная пересекает первые две в точках С и D. Докажите, что квадрат радиуса этой окружности равен произведению отрезков СА и ВD.Решение
1) Очевидно, что СОD - прямоугольный.
2) ОK2 = СK · KD, но АС = СK, ВD = KD, поэтому ОK2 = АС · ВD.
-
Объяснение нового материала.
1. Ввести понятие о вписанном угле. На закрепление этого понятия рассмотреть задание:
1) какие углы являются вписанными на рисунках?
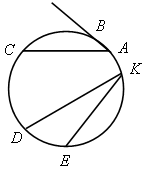
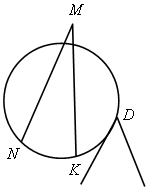
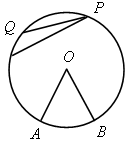
2) На какую дугу опирается вписанный угол?
2. Разобрать только первый случай возможного расположения центра окружности относительно сторон угла.
3. Обсудить доказательство двух других случаев и оставить на самостоятельное рассмотрение.
4. Обсудить идею, на которой основано доказательство двух следствий из теоремы, и предложить обучающимся самостоятельно провести его.
-
Закрепление изученного материала.
Выполнить №№ 653 (устно), 654 (устно), 655, 656, 658, 659 (устно), 661.
№ 656.РешениеПо теореме о величине вписанного
угла ![]() ВАС =
ВАС = ![]()
![]() ВС.
Рассмотрим два возможных случая расположения точки С на окружности:
ВС.
Рассмотрим два возможных случая расположения точки С на окружности:
1) точка С ![]()
![]() АВ;
АВ;
2) точка С ![]()
![]() АВ.
АВ.
В первом случае обозначим точку С через С1, во втором через С2.
1) ![]() ВС1 = 360° -
ВС1 = 360° - ![]() АС -
АС - ![]() АВ = 360° - 43° - 115° = 202°,
АВ = 360° - 43° - 115° = 202°, ![]() ВАС1 =
ВАС1 =
= ![]() ∙ 202 = 101°,
∙ 202 = 101°,
2) ![]() ВС2 =
ВС2 = ![]() АВ -
АВ - ![]() АС2 = 115° - 43° = 72°,
АС2 = 115° - 43° = 72°, ![]() ВАС2 =
ВАС2 = ![]() ∙ 72 = 36°.
∙ 72 = 36°.
Ответ: 101°, 36°.
№ 658.Решение1) ![]() ВОD =
ВОD = ![]() ВD,
ВD, ![]() АОD = 180°.
АОD = 180°.
![]() АОВ
=
АОВ
= ![]() АОD -
АОD - ![]() ВОD =
ВОD =
= 180° - 110°20′.
![]() АОВ
= 69°40′.
АОВ
= 69°40′.
2) ![]() АОВ - прямоугольный,
АОВ - прямоугольный,
![]() ОВА = 90°.
ОВА = 90°.
![]() АОВ
+
АОВ
+ ![]() ВАО = 90°.
ВАО = 90°.
Тогда ![]() ВАD =
ВАD = ![]() ВАО = 90° -
ВАО = 90° - ![]() АОВ = 90° - 69°40′.
АОВ = 90° - 69°40′.
![]() ВАD
= 20°20′.
ВАD
= 20°20′.
3) ![]() ВОD - равнобедренный с основанием ВD, так как ВО = ОD, тогда
ВОD - равнобедренный с основанием ВD, так как ВО = ОD, тогда
![]() ОВD =
ОВD = ![]() ОDВ как углы при основании.
ОDВ как углы при основании.
4) ![]() ОDВ =
ОDВ = ![]() = 34°50′.
= 34°50′.
5) ![]() АDВ =
АDВ = ![]() ОDВ = 34°50′.
ОDВ = 34°50′.
№ 661.Решение1) По теореме о величине вписанного
угла ![]() АСD =
АСD = ![]()
![]() AD.
AD.
![]() ВАС
=
ВАС
= ![]()
![]() BC.
BC.
2) ![]() АОС:
АОС:
![]() АОС
+
АОС
+ ![]() ОАС +
ОАС + ![]() АСО = 180°
АСО = 180°
![]() ОАС
= 180° -
ОАС
= 180° - ![]() ВАС.
ВАС.
3) ![]() АОD =
АОD = ![]() АОС = 180° -
АОС = 180° - ![]() ОАС -
ОАС - ![]() АСО = 180° - (180° -
АСО = 180° - (180° -
- ![]() ВАС) -
ВАС) - ![]() АСD =
АСD = ![]() ВАС -
ВАС - ![]() АСD =
АСD = ![]() (
(![]() BC
-
BC
- ![]() AD) =
AD) = ![]() (140° -
(140° -
- 52°) = 44°.
-
Итоги урока.
![]() АСВ
=
АСВ
= ![]() α
α ![]() АDВ =
АDВ = ![]() β
β
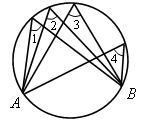
![]() 1
=
1
= ![]() 2 =
2 = ![]() 3 =
3 = ![]() 4
4 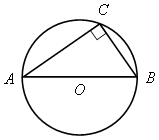 АВ - диаметр,
АВ - диаметр,
![]() АСВ
- прямой.
АСВ
- прямой.
-
Домашнее задание: вопросы 11, 12, 13, с. 187; №№ 657, 660, 663; повторить I признак подобия треугольников.
4