- Учителю
- Повторение курса теории вероятностей в 11 классе. Подготовка к ЕГЭ.
Повторение курса теории вероятностей в 11 классе. Подготовка к ЕГЭ.
Повторение курса теории вероятностей в 11 классе. Подготовка к ЕГЭ.
-
Суммой A + B событий A и B называется событие, состоящее в появлении события А, или события В, или обоих этих событий.
Пример. Пусть А - идет дождь, B - идет снег, тогда (А + В) - либо дождь, либо снег, либо дождь со снегом, т. е. осадки;
А - пошли на дискотеку; B - пошли в библиотеку, тогда (А + В) - пошли либо на дискотеку, либо в библиотеку, т. е. вышли из дома.
-
События называются несовместными, если появление одного из них исключает появление других. То есть, может произойти только одно определённое событие, либо другое.
Например, бросая игральную кость, можно выделить такие события, как выпадение четного числа очков и выпадение нечетного числа очков. Эти события несовместны.
-
Теорема сложения вероятностей несовместных событий
Теорема. Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
P (A + B) = P(A) + P(B).
Пример. В урне 30 шаров: 10 красных, 5 синих и 15 белых. Найти вероятность появления цветного шара.
Решение. Появление цветного шара означает появление либо красного, либо синего шара.
Вероятность появления красного шара (событие А)
P (A) = 10/30 = 1/3.
Вероятность появления синего шара (событие В)
P (В) = 5/30 = 1/6.
События А и В несовместны (появление шара одного цвета исключает появление шара другого цвета), поэтому теорема сложения применима.
По формуле искомая вероятность
P (A + B) = P(A) + P(B) = 1/3 + 1/6 = 1/2.
Пример. Вероятность выпадения 5 или 6 очков на игральном кубике при одном броске будет 1/3 , потому что оба события (выпадение 5, выпадение 6) несовместны и вероятность реализации одного или второго события вычисляется следующим образом: 1/6 + 1/6 =1/3.
-
Полная группа событий.
Множество несовместных событий образуют полную группу событий, если в результате отдельно взятого испытания обязательно появится одно из этих событий.
Приммер. Для игрального кубика характерно рассмотрение следующего набора:
![]() - в результате броска игрального кубика выпадет 1 очко;
- в результате броска игрального кубика выпадет 1 очко;
![]() - … 2 очка;
- … 2 очка;
![]() - … 3 очка;
- … 3 очка;
![]() - … 4 очка;
- … 4 очка;
![]() - … 5 очков;
- … 5 очков;
![]() - … 6 очков.
- … 6 очков.
События ![]() несовместны (поскольку появление какой-либо грани исключает одновременное появление других) и образуют полную группу (так как в результате испытания непременно появится одно из этих шести событий).
несовместны (поскольку появление какой-либо грани исключает одновременное появление других) и образуют полную группу (так как в результате испытания непременно появится одно из этих шести событий).
Теорема. Сумма вероятностей событий A1, A2, …, An, образующих полную группу, равна единице:
P(А1) + P(А2) + ... + P(Аn) = 1.
-
Противоположные события.
Противоположными называют два единственно возможных события, образующих полную группу. Если одно из двух противоположных событий обозначено через А, то другое принято обозначать ![]() .
.
Пример. Если при бросании кости событие А состоит в выпадении 6, то противоположное событие - это невыпадение 6, т.е. выпадение 1, 2, 3, 4 или 5.
Пример. Если А - число четное, то ![]() - число нечетное; если А - зима, то
- число нечетное; если А - зима, то ![]() - не зима (либо осень, либо лето, либо весна); если А - сдал экзамен, то
- не зима (либо осень, либо лето, либо весна); если А - сдал экзамен, то ![]() - не сдал экзамен.
- не сдал экзамен.
Теорема. Сумма вероятностей противоположных событий равна единице.
Р(А) + Р(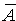 ) = 1 или Р(А) = 1 - Р(
) = 1 или Р(А) = 1 - Р(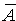 ).
).
Пример. Какова вероятность того, что при бросании двух игральных костей на них выпадает разное (не одинаковое) число очков?
Обозначим описанное событие А. Противоположным событием является событие 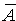 , состоящее в том, что на обеих костях выпало одинаковое число очков. Событию
, состоящее в том, что на обеих костях выпало одинаковое число очков. Событию 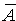 благоприятствуют шесть элементарных событий: (1;1), (2;2), (3;3), (4;4), (5;5), (6;6). Вероятность каждого из этих элементарных событий
благоприятствуют шесть элементарных событий: (1;1), (2;2), (3;3), (4;4), (5;5), (6;6). Вероятность каждого из этих элементарных событий 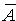 . Значит, Р(
. Значит, Р(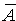 ) =
) = 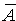 . Тогда Р(А) = 1 - Р(
. Тогда Р(А) = 1 - Р(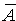 )= 1 -
)= 1 - 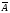 .
.
-
Зависимые и независимые события. Условная вероятность.
Два события А и В называются независимыми, если вероятность появления каждого из них не зависит от того, появилось другое событие или нет.
Пример. Монета брошена два раза. Событие А - выпал «герб» при первом броске, событие В - выпал «герб» при втором броске. События А и В независимы.
События А и В называются зависимыми, если вероятность наступления одного из них зависит от того, произошло или нет другое событие.
Если вероятность события В вычисляется в предположении, что событие А уже произошло, то такая вероятность называется условной вероятностью события В по отношению к событию А. Обозначение: РА(В).
Пример. В конверте лежало 4 открытки с видами Петербурга и 3 открытки с видами Москвы. Пусть событие А - извлечение открытки с видами Петербурга, событие В - извлечение открытки с видами Москвы. Рассмотрим вероятности. Связанные с этими событиями.
-
Если открытка извлечена только в начале один раз, то Р(А) =
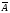 , Р(В) =
, Р(В) = 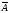 .
. -
Если две открытки последовательно извлекаются из конверта без возврата в него, то:
а) если сначала вытащили открытку с видом Петербурга, а затем с видом Москвы, то РА(В) = 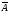 ;
;
б) если сначала вытащили открытку с видом Москвы, а затем с видом Петербурга, тогда РВ(А) = 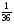 .
.
-
Произведение вероятностей.
Произведением двух событий А и В называют событие АВ, состоящее в совместном появлении (совмещении) этих событий.
Пример. Пусть А - из урны вытянули белый шар, B - из урны вытянули белый шар, тогда АВ - из урны вытянули два белых шара; если А - идет дождь, B - идет снег, то АB - дождь со снегом; А - число четное, B - число кратное 3, тогда АB - число кратное 6.
Теорема умножения для независимых событий
Теорема. Вероятность произведения двух независимых событий А и В равна произведению их вероятностей:
P(AB) = P(A) · P(B).
Пример. Игральный куб подбрасывают два раза. Какова вероятность, что в первом броске выпадет 2 очка, а во втором 6?
Пусть событи е А - выпадение 2 очков, событие В - выпадение 6 очков, событие С - выпадение в первом броске 2 очков, а во втором 6 очков.
События А и В независимы, так как наступление одного события не зависит от наступления другого события. Тогда так как Р(А) = 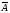 и Р(В) =
и Р(В) = 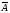 , то Р(С) = Р(А) · Р(В) =
, то Р(С) = Р(А) · Р(В) = 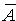 .
.
Теорема умножения для зависимых событий.
Теорема. Если события А и В являются зависимыми, то вероятность их произведения равна произведению вероятности одного из них на условную вероятность другого
P (AB) = P (A) · PA(B).
Пример. В конверте лежало 4 открытки с видами Петербурга и 3 открытки с видами Москвы. Пусть событие А - извлечение первый раз видов Петербурга, событие В - извлечение первый раз видов Москвы. Пусть событие С состоит в том, что вначале вытащили вид Петербурга, затем вид Москвы. Тогда событие С по определению умножения равно А·В. Очевидно, что в данном случае события А и В зависимы. Покажем это.
-
Если вначале извлекут вид Петербурга Р(А) =
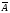 , то вероятность того, что затем извлекут вид Москвы Р(В) =
, то вероятность того, что затем извлекут вид Москвы Р(В) = 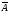 (по классическому определению вероятности).
(по классическому определению вероятности). -
Если же вначале извлекут вид Москвы, то вероятность того, что второй раз извлекут вид Москвы, будет равна
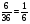 . Зависимость более чем очевидна.
. Зависимость более чем очевидна.
Значит нужно воспользоваться теоремой о формуле произведения зависимых событий, т.е. Р(С) = P (A) · PA(B). Таким образом, Р(С) = 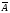 .
.
Пример. В читальном зале имеется 6 учебников по информатике, из которых три в переплете. Библиотекарь наудачу взял два учебника. Найти вероятность того, что оба учебника окажутся в переплете.
Решение. Рассмотрим следующие события:
А1 - первый взятый учебник в переплете;
A2- второй взятый учебник в переплете.
Событие A = A1 · A2, состоит в том, что оба взятых учебника в переплете. События А1 и А2 являются зависимыми, так как вероятность наступления события А2 зависит от наступления события А1. Поэтому, для вычисления вероятности воспользуемся формулой произведения зависимых событий.
Вероятность наступления события А1 в соответствии с классическим определением вероятности:
P (А1) = m / n = 3/6 = 0,5.
P А1 (А2) определяется как условная вероятность наступления события А2 при условии, что событие А1 уже наступило:
P А1 (А2) = 2/5 = 0,4.
Тогда искомая вероятность наступления события А:
P (А) = 0,5 · 0,4 = 0,2.
-
Теорема сложения вероятностей совместных событий
Два события называются совместными, если появление одного из них не исключает появления другого в одном и том же испытании.
Пример. А - появление четырех очков при бросании игральной кости; В - появление четного числа очков. Событие А и В - совместны.
Теорема. Вероятность появления хотя бы одного из двух совместных событий А и В равна сумме вероятностей этих событий без вероятности их совместного появления:
P (A + B) = P (A) + P (B) - P (AB).
Пример. Два студента читают книгу. Первый студент дочитает книгу с вероятностью - 0,6; второй - 0,8. Найти вероятность того, что книга будет прочитана хотя бы одним из студентов.
Решение. Вероятность того, что книга будет прочитана каждым из студентов не зависит от результата отдельно взятого студента, поэтому события А (первый студент дочитал книгу) и B (второй студент дочитал книгу) независимы и совместны. Искомую вероятность находим по формуле сложения вероятностей совместных событий.
Вероятность события АB (оба студента дочитали книгу):
P (AB) = P (A) · P (B) = 0,6 · 0,8 = 0,48.
Тогда
P (A + B) = 0,6 + 0,8 - 0,48 = 0,92.
Пример. В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдем вероятность того, что к концу дня кофе закончится хотя бы в одном из автоматов (то есть или в одном, или в другом, или в обоих сразу).
Вероятность первого события «кофе закончится в первом автомате» также как и вероятность второго события «кофе закончится во втором автомате» по условию равна 0,3. События являются совместными.
Вероятность совместной реализации первых двух событий по условию равна 0,12.
Значит, вероятность того, что к концу дня кофе закончится хотя бы в одном из автоматов есть 0,3 + 0,3 - 0,12 = 0,48.
Пример. В школе 1400 учеников, из них 1200 учеников умеют кататься на лыжах, 952 ученика умеют кататься на коньках. Не умеют кататься ни на лыжах, ни на коньках 60 учеников. Какова вероятность, что ученик умеет кататься и на лыжах, и на коньках?
Обозначим Е - все ученики данной школы. Пусть событие А - умение учеников кататься на лыжах. Событие В - умение учеников кататься на коньках. Событие АВ - умение учеников кататься и на лыжах и на коньках. Событие А+В - умение учеников кататься или на лыжах, или на коньках.
Т.к. 60 учеников не умеют кататься ни на лыжах, ни на коньках, то учеников, которые умеют кататься или на лыжах, или на коньках 1400 - 60 = 1340. Тогда Р(А) = 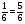 , Р(В) =
, Р(В) = 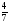 ; Р(А+В) =
; Р(А+В) = 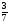 . Но
. Но
Р(А+В) = Р(А) + Р(В) - Р(АВ). Тогда Р(АВ) = Р(А) + Р(В) - Р(А+В). Так как события А и В - зависимые со бытия, то Р(АВ) = 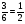 .
.
-
Формула полной вероятности.
Если событие А может произойти только при выполнении одного из событий В1, В2, …, Вn которые образуют полную группу несовместных событий, то вероятность события А вычисляется по формуле
Р(А) = Р(В1) · РВ1(А) + Р(В2) · РВ2(А) + … + Р(Вn) · РВn(А).
Эта формула называется формулой полной вероятности.
Пример. В магазине продаются электролампы производства трех заводов, причем доля первого завода - 30, второго - 50, третьего - 20. Брак в их продукции составляет соответственно 5, 3 и 2. Какова вероятность того, что случайно выбранная в магазине лампа оказалась бракованной.
Пусть событие В1 состоит в том, что выбранная лампа произведена на первом заводе, В2 - на втором, В3 - на третьем заводе. Очевидно:
P(В1) = 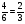 , P(В2) =
, P(В2) =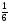 , P(В3) =
, P(В3) =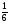 .
.
Пусть событие А состоит в том, что выбранная лампа оказалась бракованной; РВ1(А) означает событие, состоящее в том, что выбрана бракованная лампа из ламп, произведенных на первом заводе, Р(В2) - на втором заводе, Р(В3) - на третьем заводе. Из условия задачи следует:
РВ1(А)= 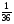 ; РВ2(А) =
; РВ2(А) =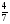 ; РВ3(А) =
; РВ3(А) = 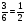 .
.
По формуле полной вероятности получаем
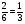 =0,034.
=0,034.
Список литературы.
-
Тюрин Ю.Н., Макаров А.А., Высоцкий И.Р., Ященко И.В. Теория вероятностей и статистика. ОАО «Московский учебник». М., 2008.
-
Шахмейстер А.Х. Комбинаторика. Статистика. Вероятность. МЦНМО. М., 2010.
-