Конспект урока по алгебре (7 класс)

Муниципальное общеобразовательное учреждение

средняя общеобразовательная школа № 81 городского округа Тольятти

План - конспект открытого

урока математики

Тема: «Cистемы двух линейных уравнений с двумя переменными»

7 класс»

Класс 7 «Б»

Учитель Зотова Лариса Николаевна

г. о. Тольятти 2014 год

Цели урока:

• обучающая:

- закрепление и углубление знаний и умений решения систем двух линейных уравнений с двумя переменными;

• развивающая:

- развитие мыслительных способностей учащихся, умения действовать в нестандартной ситуации;

• воспитательная:

- воспитание внимательности, активности, самостоятельности в работе;

- воспитание интереса к предмету.

Оборудование: компьютер, проектор.

Тип урока: формирование и совершенствование умений и навыков.

Формы работы: коллективная, индивидуальная.

План урока:

1. Организационный момент.

2. Актуализация знаний. Устная работа.

3. Формирование знаний и умений.

4. Подведение итогов.

5. Домашнее задание.

Ход урока:

1. Организационный момент.

Слайды № 1, 2

2. Актуализация знаний.

Устная работа.

1) На доске записана система.

Вызываются 3 ученика и решают эту систему графическим способом, способом подстановки и способом сложения.

В это время с классом идет фронтальная устная работа. "Легкая разминка". Используется проектор.

Слайд № 3

а) Как называются такие уравнения? (линейные уравнения с двумя переменными)

1) х + у = 8 2)х - у = 4 3)4х + 2у = 6.

- Что является графиком линейного уравнения? (прямая)

- Как построить график линейного уравнения? (выразить у через х, найти координаты двух точек)

Слайд № 4

Из каждого уравнения выразите у через х , х через у.

Слайды № 5, № 6

б) Разложите на множители:

1)х² - 2х 2)х² - 4 3)х² + 4х +4

4)х² -6х + 9 5)х³ - 8 6)х³ + 1.

- Какими способами разложить данные многочлены на множители? (вынесением общего множителя за скобки, по формулам сокращенного умножения, способом группировки)

Слайд № 7

в) Решите уравнение:

1)(х - 1)(х + 2) = 0 2)х² = 4 3)2х² = 18.

г) Далее учащимся предлагается ответить на опросы:

- Что вы понимаете под словом система уравнений?

- Что называется решением системы линейных уравнений с двумя переменными?

- Что значит решить систему уравнений?

- Какие способы решения систем уравнений вы знаете?

После этого каждый ученик, выполнявшие задание у доски рассказывают алгоритм решения систем уравнений графическим способом, способом подстановки и способом сложения. Остальные слушают, проверяют правильность решения.

- Ребята, как проверить правильность решения системы?

- На ваш взгляд, каким способом легче решается данная система? (способом подстановки, способом сложения).

- Согласна, но решая графическим способом, мы наглядно можем увидеть, имеет ли система уравнений решений или нет. Поэтому этот способ служит геометрической иллюстрацией наличия или отсутствия решения системы уравнений.

- А как еще можно выяснить, имеет ли система уравнений решение или нет? (выразить из каждого уравнения у через х и сравнить угловые коэффициенты)

3. Формирование знаний и умений.

Существует, ребята, еще один способ решения систем уравнений, которые мы с вами еще не рассматривали. Это метод - метод перебора или подбора.

Например, дается система .

Можно легко подобрать значение х и у: х = 4; у = 3.

Все эти способы решения систем уравнений знали люди давно. Точной даты не известно, но они имеются в книге Ньютона "Всеобщая арифметика", которая была издана в 1707 году.

Далее следует фронтальная работа с классом с записью решения на доске. Решение задач повышенного уровня.

Требуется решить системы уравнений различными способами.

1.

Рассматриваются способы решения: подстановки, перебора, графический.

1 вариант - решают систему способом подстановки

2 вариант - решают систему перебором

3 вариант - решают систему графическим способом.

2.

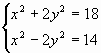
Способы решения: подстановки, сложения (по вариантам).

- Где находит применение системы уравнений? (при решении задач). Повторяется схема решения задач с помощью систем уравнений.

Занимательные задачи.

Слайд № 8

1) Предлагается решить старинную задачу "Лошадь и мул":

Лошадь и мул шли бок о бок с тяжелой поклажей на спине. Лошадь жаловалась на свою непомерно тяжелую ношу. "Чего ты жалуешься? - отвечал ей мул. - Ведь если я возьму у тебя один мешок, ноша моя станет вдвое тяжелее твоей. А вот если бы ты сняла с моей спины один мешок, твоя поклажа стала бы одинаково с моей".

Скажите же, мудрые математики, сколько мешков несла лошадь и сколько нес мул?

Разбирается решение задачи.

Пусть лошадь несла х мешков, а мул - у мешков. Если мул возьмет один мешок у лошади, то у него будет (у + 1), а у лошади останется (х - 1) мешков. Так как ноша у мула станет вдвое тяжелее, то составим уравнение 2(х - 1) = у + 1. Если лошадь снимет с мула один мешок, то у нее будет (х + 1), а у мула останется (у - 1) мешков. Так как ноша у них станет одинаковой, то получим уравнение х + 1 = у - 1. Составим и решим систему уравнений.

Слайды № 9, № 10

Система решается самостоятельно, затем осуществляется проверка по слайду.

Слайд № 11.

2) Внимание на следующий слайд

Слайд № 12

Сейчас вы увидите только часть решения некоторой задачи. Попробуйте по этой части сформулировать всю задачу.

Пусть стороны прямоугольника будут х и у см. Тогда имеем:

Ученики составляют задачу, решить предлагается дома.

Задача. Периметр прямоугольника равен 20 см, а одна из сторон больше другой на 4 см. Найдите стороны прямоугольника.

4. Итог урока.

Итак, ребята, мы заканчиваем изучение темы "Системы линейных уравнений".

А сейчас ответьте, пожалуйста, на такие вопросы:

- что нового вы узнали сегодня на уроке?

- чему научились?

(Выслушиваются ответы учащихся, выставляются оценки за урок)

5. Домашнее задание.

1. решить задачу № 2

2. № 1134, № 1109 из задачника (авторы А. Г. Мордкович, Т. Н. Мишустина,

Е. Е. Тульчинская)