Равносильность неравенств (объяснение материала)

Урок алгебры (под редакцией А.Г. Мордковича, 2013) в 11 классе по теме "Равносильность неравенств"(базовый уровень)

Урок 1: Объяснения нового материала

Три пути ведут к знанию:

путь размышления - это путь

самый благородный,

путь подражания - это путь

самый легкий и

путь опыта - это путь

самый горький.

Конфуций

Тип урока: изучение нового материала.

Оборудования: учебники, блокноты, интерактивная доска, карточки с заданиями.

Цели и задачи урока

Цели :

Образовательная: ввести определение равносильности, записать теоремы равносильности.

Развивающая: развивать память, наблюдательность, логическое мышление, математическую речь учащихся, умение анализировать и сравнивать, развивать познавательный интерес к предмету, развивать умение выделять главное, логически излагать мысли.

Воспитательная: воспитывать коммуникативную культуру учащихся, навыки коллективной деятельности, сотрудничества, взаимопомощи, воспитание дисциплинированности, аккуратности записей в тетради, внимательности, активизировать деятельность учащихся на уроке.

Задачи:

а)Обучающая - на основе имеющихся у учащихся знаний подвести учащихся к понятию равносильности неравенств, определить вместе с ними это понятие;

б) развивающая - формирование приемов обобщения, алгоритмизации;

в) воспитывающая - воспитывать умение участвовать в диалоге, понимать точку зрения собеседника, признавать право на иное мнении, показ практической применимости математических знаний.

Ход урока

1.Организационный момент (сообщение темы и цели урока).

Приветствие, проверка отсутствующих в классе. Проверка выполнения домашнего задания. Как справились с домашним заданием? Что вызвало затруднение?

2.Актуализация знаний

1) Опорные знания: производная, таблица производных, физический смысл производной.

2) Связь с прошлой темой: на уроке используются таблицы производной, вычисляются производные функций.

Задание классу:

1. Вычислить производные следующих функций:

(1)^/ = ((2х-3)⁶)^/=

(х)^/ = ((х⁵+20))^/=

(30х)^/= (Соs 3х)^/=

(х³)^/= ( 5х¹⁰)^/=

2. Назвать физический смысл производной.

Ребята я предлагаю сегодня на уроке привести в систему, обобщить и расширить знания о равносильности уравнений и неравенств системам.

3. Формулирование новой темы, определение основных целей.

Сегодня мы с вами рассмотрим тему: «Равносильность уравнений». Узнаем, что такое равносильность уравнений, дадим определение «равносильности», запишем с вами определения и теоремы равносильности, рассмотрим примеры.

4. Объяснение нового материала.

Начнем, с определения равносильных неравенств:

Решением неравенства f(x)>g(x) называют всякое значение переменной x, которое обращает заданное неравенство с переменной в верное числовое неравенство.

Термин решение используют в трёх смыслах: как общее решение, как частное решение и как процесс.

Опр.: Два неравенства с одной переменной f(x)>g(x) и p(x)>h(x) называют равносильными, если их решения (т.е. множества частных решений) совпадают.

Использование знака > непринципиально, может быть любой другой знак неравенства как строгого, так и нестрогого.

Опр.: Если решение неравенства f(x)>g(x) (1) содержится в решении

неравенства p(x)>h(x), (2) то неравенство (2) называют следствием неравенства (1).

Неравенство x2>9 является следствием неравенства 2x>6.В самом деле, решив каждое неравенство, получим:

x2−9>0(x−3)⋅(x+3)>0x∈(−∞;−3)∪(3;+∞) и

2x>6x>3x∈(3;+∞)

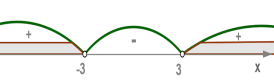
Решение второго неравенства является частью решения первого, поэтому первое неравенство - следствие второго неравенства.

Решение неравенств, встречающихся в школьном курсе, основано на шести теоремах о равносильности:

Теорема 1.

Если какой-либо член неравенства перенести из одной части неравенства в другую с противоположным знаком, оставив знак неравенства без изменения, то получится неравенство, равносильное данному.

Теорема 2.

Если обе части неравенства возвести в одну и ту же нечётную степень, оставив знак неравенства без изменения, то получится неравенство, равносильное данному.

Теорема 3.

Показательное неравенство af(x)>ag(x) равносильно:

а) неравенству того же смысла f(x)>g(x), если a>1;

б) неравенству противоположного смысла f(x)<g(x), если 0<a<1

Теорема 4.

a) Если обе части неравенства f(x)>g(x) умножить на одно и то же выражение h(x), положительное при всех x из области определения (области допустимых значений переменной) неравенства f(x)>g(x), оставив при этом знак неравенства без изменения, то получится неравенство f(x)⋅h(x)>g(x)⋅h(x), равносильное данному.

б) Если обе части неравенства f(x)>g(x) умножить на одно и то же выражение h(x), отрицательное при всех x из области определения неравенства f(x)>g(x), изменив при этом знак неравенства на противоположный, то получится неравенство f(x)⋅h(x)<g(x)⋅h(x), равносильное данному.

Теорема 5.

Если обе части неравенства f(x)>g(x) неотрицательны в области его определения (в ОДЗ), то после возведения обеих частей неравенства в одну и ту же чётную степень n получится неравенство того же смысла f(x)n>g(x)n, равносильное данному.

Теорема 6.

Если f(x)>0 и g(x)>0, то логарифмическое неравенство logaf(x)>logag(x) равносильно:

а) неравенству того же смысла f(x)>g(x), если a>1;

б) неравенству противоположного смысла f(x)<g(x), если 0<a<1.

5. Закрепление нового материала.

Пример 1. ]</</font>

Хотелось бы, конечно, возвести обе части в квадрат, это возможно только при неотрицательности обеих частей. Но что же нам делать с теми х, для которых правая часть отрицательна? Для всякого решения неравенства правая часть больше левой, являющейся неотрицательным числом в ОДЗ, и, стало быть, сама неотрицательна. Итак, следствием нашего неравенства будет такая система:

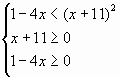, где возведенное в квадрат неравенство, неотрицательность правой части ОДЗ

Пример 2.

Решение. Здесь опять же заведомо можно возвести в квадрат только тогда, когда . Однако теперь уже нельзя отбросить тех, для которых правая часть отрицательна:

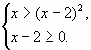Итак, у нас получилось два случая: если правая часть неотрицательна , то из нашего неравенства следует система Если же правая часть отрицательна, то неравенство верно на ОДЗ (ведь тогда отрицательная правая часть должна быть меньше положительной левой, а это верно на ОДЗ) и следует система где неотрицательность меньшей части и ОДЗ.

Неравенство равносильно такой совокупности двух систем:

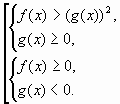
Пример 3.

Решение. На сей раз обе части неравенства всегда неотрицательны, так что возведение в квадрат дает неравенство, равносильное исходному на его естественной области определения. Возведение в квадрат дает неравенство: , (8) область определения дает неравенства: (9) и (10).

Мы не учитываем (10), т.к. если правое, меньшее, подкоренное выражение неотрицательно, то левое и подавно неотрицательно. Стало быть, из неравенства следует такая система:

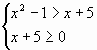, возведенное в кв. неравенствово и неотрицательность меньшей части.

Неравенство равносильно системе:

6. Подведение итогов.

Сегодня мы с вами рассмотрели тему: «Равносильность неравенств». Узнали, что такое равносильность уравнений, дали определение «равносильности», записали с вами определения и теоремы равносильности, рассмотрели примеры.

1. Было ли интересно на уроке?

2. Все ли было на уроке понятно?

7. Домашнее задание.

Читать § 55 по учебнику (под редакцией А.Г. Мордковича, 2013); решить № 1665(в), № 1674 (б), № 1675 (г) по задачнику(под редакцией А.Г. Мордковича, 2013).