Тема урока: Теорема синусов

Тема урока: Теорема синусов

Цель урока: дать определение теореме синусов

Задачи урока: решение задач по данной теме

Ход урока:

1 этап: Орг момент, приветствие, проверка дом задания

2 этап: новая тема

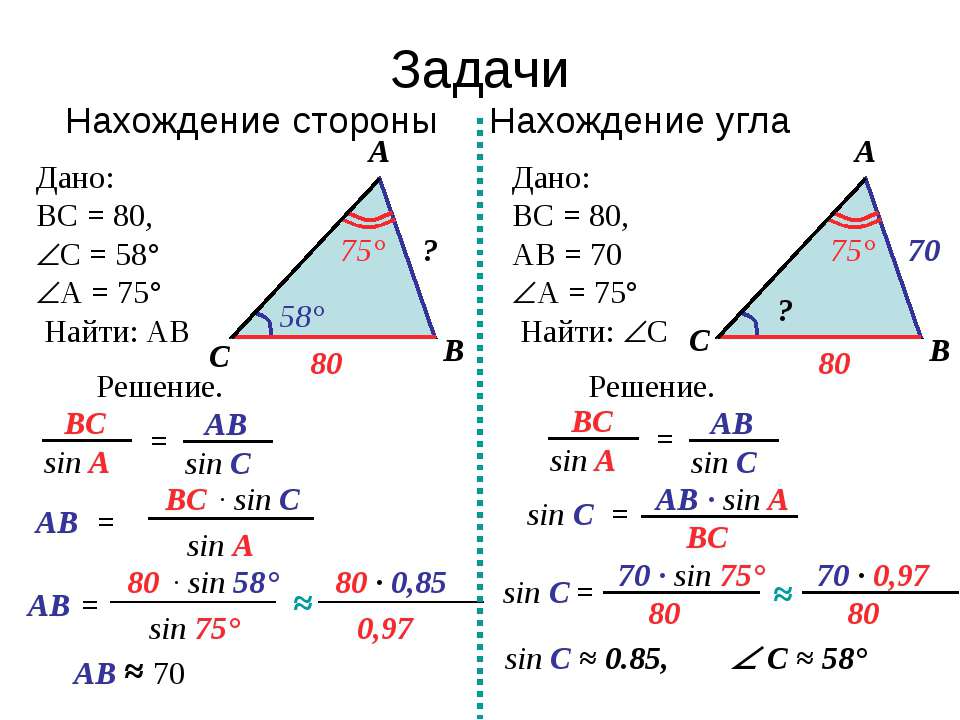
</<font color="#000000">Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов.

Доказательство: Пусть ABC - треугольник со сторонами a, b, c и противолежащими углами α, β, γ (рис. 265). Докажем, что



Опустим из вершины С высоту CD. Из прямоугольного треугольника ACD, если угол α острый, получаем: CD=b*sinα (рис. 265, a). Если угол α тупой, то CD=b*sin(180°-α)=b*sinα (рис. 265, б). Аналогично из треугольника BCD получаем CD=a*sinβ. Итак, a*sinβ=b*sinα. Отсюда . Аналогично доказывается равенство . Для доказательства нужно провести высоту треугольника из вершины А. Теорема доказана.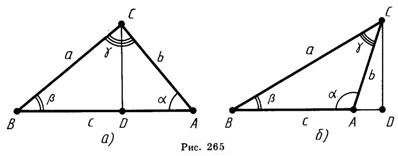

Каждое из трех отношении: - равно 2R, где R - радиус окружности, описанной около треугольника.

Доказательство: Проведем диаметр BD (рис. 266). По свойству углов, вписанных в окружность, угол при вершине D прямоугольного треугольника BCD равен либо α, если точки А и D лежат по одну сторону от прямой ВС (рис. 266, а), либо 180°-α, если они лежат по разные стороны от прямой ВС (рис. 266, б). В первом случае BC=BD*sinα, во втором ВС=BD*sin(180°-α). Так как sin(180°-α)=sinα, то в любом случае a=2R*sinα. Следовательно, что и требовалось доказать.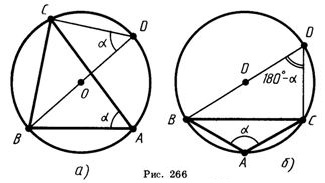

3 тап: решение задач по данной теме: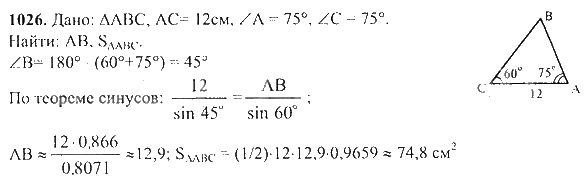

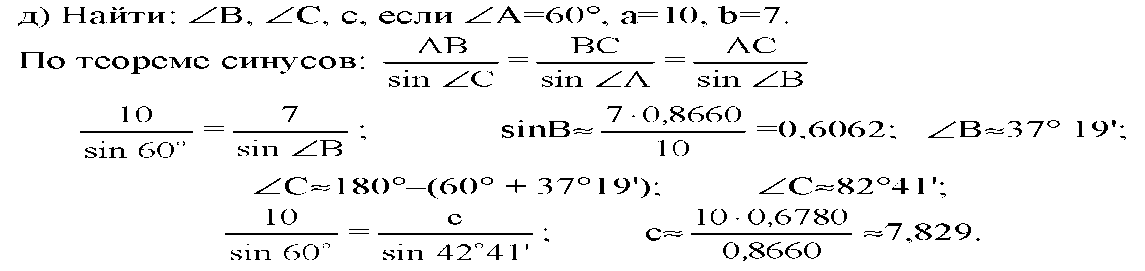
4 этап: подведение итогов

5 этап: домашнее задание: