- Учителю
- Конспект урока математики в 6 классе по теме «Отношения и пропорции»
Конспект урока математики в 6 классе по теме «Отношения и пропорции»
Кирюшина Елена Петровна,
учитель математики МБОУ СОШ №2 села Ермолаево
Конспект урока математики в 6 классе
по теме «Отношения и пропорции»
Цели:
Образовательные
-
закрепить понятие пропорции и ее членов, чтение пропорции, составление пропорции из отношений, основное свойство пропорции;
-
закрепить навыки решения задач с помощью пропорции;
-
обратить особое внимание учащихся на применение пропорции в различных областях деятельности, важность изучения указанной темы для дальнейшего обучения в школе.
Развивающие
-
формировать умение применять приемы: сравнения, обобщения, выделения главного, переноса знаний в новую ситуацию;
-
развивать математический кругозор, логическое мышление и речь, внимание и памяти;
-
способствовать выработке навыков контроля и взаимоконтроля.
Воспитательные
-
создать у учащихся положительную мотивацию к уроку математики, путем вовлечения каждого ученика в активную деятельность;
-
воспитывать потребность оценивать свою деятельность и работу товарищей;
-
помочь осознать ценность совместной деятельности;
-
воспитывать культуру речи, внимание к точности формулировок.
Тип урока: урок закрепления изученного материала.
Методы обучения: частично-поисковый, взаимопроверка и самопроверка.
Формы организации урока: индивидуальная, фронтальная, работа в парах.
Оборудование: компьютер, мультимедийный проектор, интерактивная доска, презентация, раздаточный материал.
Общая структура урока
-
уточнение направлений актуализации изученного материала;
-
сообщение темы, цели и задач урока, мотивация обучения;
-
воспроизведение изученного и его применение в стандартных условиях;
-
перенос приобретенных знаний и их первичное применение в новых или измененных условиях с целью формирования умений;
-
подведение итогов урока;
-
постановка д/з.
Ход урока.
1. Приветствие учащихся.
2. Устная работа.
2.1. С чего, как правило, нужно начинать новый день? Верно, с утренней гимнастики. Мы тоже с вами начнем урок с гимнастики для ума. Посмотрите на экран, что нужно сделать? (прочитать анаграммы и найти лишнее слово):
тамкамтиае - математика;
зифкиа - физика;
огяигерфа - география;
тбувсоа - автобус;
ялогбоии - биология, лишнее слово - автобус. (слайд 2)
2.2. А на завтрак вы угостите друг друга напитком. (работа в парах, запись в тетрадях: число, классная работа. №1)
Один ученик делает напиток из 15 г быстрорастворимого напитка «Золотой шар» и 750 г воды, а второй - из 30 г «Золотого шара» и 1500 г воды. Что вы можете сказать о вкусе приготовленных напитков? (Вкус один и тот же). Почему? (отношения величин сухого напитка к воде одинаковы в обоих случаях).
А если два отношения равны, то мы можем составить верную пропорцию.
3. Сообщение темы урока. Как можно сформулировать тему нашего урока? (Отношения и пропорции). На предыдущих уроках мы изучили основные понятия по этой теме, применяли свойство пропорции при решении задач. Сегодня мы продолжим эту работу, будем решать задачи, применяя основное свойство пропорции, а так же познакомимся с практическим применением пропорции.
3.1. Для успешной работы по решению задач нам необходимо хорошо знать теоретический материал:
-
Что называется пропорцией?
-
А что такое отношение?
-
Как найти неизвестный член пропорции?
-
В чем заключается основное свойство пропорции?
-
Какие виды пропорциональной зависимости вы знаете?
4. Применение знаний в стандартных условиях:
4.1.Устные упражнения:
-
Даны равенства 5,3 × 2 = 10,6 × 1; 7 : 2 = 3 + 0,5 ; 18 : 6 = 30 : 10. Какие из них являются пропорциями? (слайд 3)
-
Прочитать пропорцию и назвать крайние и средние члены: 4,2 : 2,1=4 : 2. (слайд 4)
-
Составьте верную пропорцию из чисел, обозначающих: (слайд 5)
1. количество цветов в спектре радуги;
2. НОК(14;21);
3. удвоенное количество месяцев в году;
4. количество цветов на российском флаге, увеличенное на единицу.
-
Определите, является ли прямо пропорциональной, обратно пропорциональной или не является пропорциональной зависимость между величинами (слайды 6 - 11).
-
Запишите пропорцию, если
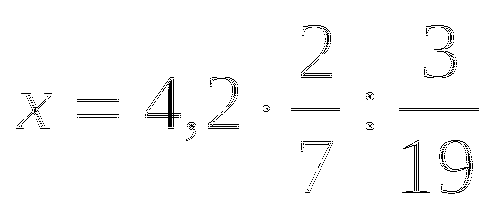 (слайд 12)
(слайд 12)
4.2. Решение задач (по рядам): (слайд 13)
1ряд: Во время распродажи магазин делает скидку 20% на все товары. Сколько рублей стоил свитер до распродажи, если во время распродажи его купили за 600 рублей?
100%-20%=80%,
100% - х руб.,
80% - 600 руб.
80 х =100*600, х = 750 руб.
2 ряд: После того, как цены на посуду в магазине были подняты на 20%, чашка стала стоить 132 р. Сколько рублей стоила чашка до повышения цены?
100%+20%=120%,
132 руб. - 120%,
х руб. - 100%,
120х=132*100, х=110 руб.
3 ряд: В июле в магазин привезли 500 учебников по биологии, а в августе на 75% больше. Сколько учебников по биологии привезли в магазин в августе?
100%+75%=175%,
500 уч. - 100%,
х уч. - 175%,
100х = 500*175, х=875 уч.
Я вам говорила, что темы «Проценты» и «Пропорции» изучаются только в 6 классе, но задачи на эти темы включены в экзаменационные работы за курс 9 и 11 классов. Эти задачи, которые мы с вами сейчас решили, я взяла из банка задач ГИА по математике в 2014 году. В демонстрационном варианте задачи такого типа стоят под №16.
5. Перенос приобретенных знаний и их первичное применение в новых или измененных условиях с целью формирования умений:
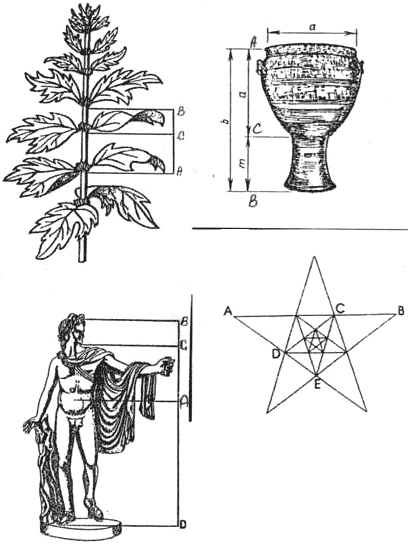
5.1. Учение об отношениях и пропорциях особенно успешно развивалось в IV веке до н.э. в Древней Греции. С пропорциями связывались представления о красоте, порядке и гармонии, о созвучных аккордах в музыке. Теория отношений и пропорций была подробно изложена в книге Евклида «Начала», там же приводится доказательство основного свойства пропорции. Пропорциональность в природе, искусстве, архитектуре означает соблюдение определенных соотношений между размерами отдельных частей скульптуры, всего здания, растения и является непременным условием правильного и красивого изображения предмета.
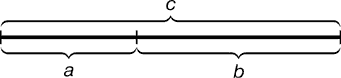
Золотым сечением и даже «божественной пропорцией» называли математики древности деление отрезка, при котором длина его большей части относится к длине всего отрезка, как длина меньшей части к большей. Это отношение ≈ 0, 618. (слайд 14)
![]()
Золотое сечение - чудо математики. Древние архитекторы многогранно использовали золотое сечение в своих работах. Одним из красивейших произведений древнегреческой архитектуры является Парфенон - главный храм в древних Афинах, посвящённый покровительнице этого города богине Афине. Построен в 5век до н.э. Отношение высоты здания к его длине равно 0,618, т.е. золотому сечению, а это значит, что древние греки жили в гармонии с окружающим нас миром. В фасаде Парфенона тоже присутствуют пропорции золотого сечения. (слайд 15)
Рассматривая расположение листьев на общем стебле растений можно заметить, что между каждыми двумя парами листьев третья расположена в месте золотого сечения. (слайд 16)
Замечательный пример «золотого сечения» представляет собой правильный звездчатый пятиугольник, который можно найти в вавилонских рисунках. Для школы Пифагора звездчатый пятиугольник служил опознавательным знаком и символом здоровья.
Интересно, что внутри пятиугольника можно продолжить строить пятиугольники, и это отношение будет сохраняться. Звездчатый пятиугольник называется пентаграммой. (слайд 17)
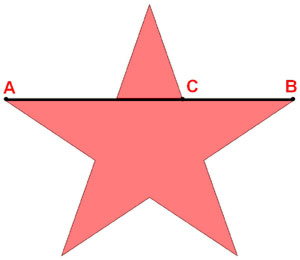
.
![]()
5.2 Физминутка:
Рука - вперёд, на среднем пальце - взгляд,
И так до четырёх считаю.
Теперь я руку в сторону переведу, но так,
Что головою не верчу и не качаю.
Лишь за рукою движется мой взгляд по всей горизонтали,
Глазам ведь нужно отдохнуть, они чуть - чуть устали!
5.3. Исследовательская работа:
У вас на столе лежат звездочки разных размеров. Измерьте нужные отрезки. Составьте пропорцию и проверьте равенство.
Какое число у вас получилось? (![]() 0,6) Почему у всех примерно одинаковый ответ, ведь звездочки разной величины? (Отношения равны. В этом и заключается свойство "Золотого сечения")
0,6) Почему у всех примерно одинаковый ответ, ведь звездочки разной величины? (Отношения равны. В этом и заключается свойство "Золотого сечения")
5.4. Самостоятельная работа с последующей взаимопроверкой (работа в парах).
I вариант
1. Решить уравнение:
6,4:0,16= 4:х
1) 10; 2) 2,5; 3) 0,1; 4) 1.
2. Решить задачу:
Для 10 порций салата требуется 200 г лука. На сколько порций хватит 60 г лука?
1) 3; 2) 4; 3) 2; 4) 9.
3. При каком х верна пропорция
![]()
1) 31; 2) 13; 3) 23; 4) 11.
II вариант
1. Решить уравнение:
0,75:1,5= 5:х
1) 10; 2) 2,5; 3) 0,1; 4) 1
2. Решить задачу:
6 рабочих могут выполнить работу за 12 дней. Сколько ещё надо нанять рабочих, чтобы выполнить эту работу за 8 дней?
1) 3; 2) 4; 3) 2; 4) 9.
3. При каком х верна пропорция
![]()
1) 31; 2) 13; 3) 23; 4) 11
Ответы: (слайд18)
вариант
№1
№2
№3
1 вариант
3
1
2
2 вариант
1
4
4
6. Подведение итогов.
-
О каком математическом понятии мы сегодня говорили? (О пропорции).
-
Что же такое пропорция?
-
В чем заключается основное свойство пропорции?
-
В каких областях деятельности мы сегодня рассмотрели применение пропорции? (В искусстве, архитектуре, строении растений, в сельском хозяйстве).
Это далеко не все области, где применима пропорция. И вы, переходя из класса в класс, в этом убедитесь. Вы встретитесь с пропорцией на уроках химии, физики, геометрии. Как вы считаете, нужную тему вы изучили?
7. Домашнее задание.
№794 - задача на составление пропорции,
№803 (в, г) - уравнения,
№815 - задача на % содержание.
Творческое задание - найти в окружающих вас предметах, предмет, в котором соблюдается отношение золотого сечения (ваза, предмет мебели, цветок и т.д.)