Урок по математике для 9 класса по теме «Квадратичная функция» (Подготовка к ГИА)

Урок обобщения и систематизации знаний в 9 классе по теме по теме «Квадратичная функция».

Тема «Квадратичная функция» - важная тема курса математики. Знание её необходимо как при дальнейшем изучении предмета, так и при решении заданий ГИА. На уроке обобщаются и систематизируются знания по данной теме.

В школе при санатории «Чёрная речка» обучаются дети из разных школ Ярославской области. Учитывая данную особенность, разбиваю учеников класса на группы для выполнения заданий, посильных каждому (индивидуальный подход к ребёнку).

Дифференциация обучения заключается в том, что, обучаясь в одном классе санаторной школы, но по разным программам и учебникам, ученики могут усваивать материал разными способами и на разных уровнях, приобретая при этом умение самостоятельно находить способы решения задач. На протяжении всего урока по теме «Квадратичная функция» проводится дифференцированная работа двух видов: дифференциация по темам изученного материала (деление на группы) и дифференциация по уровням владения материалом внутри одной группы ( А, В, С ).

Диагностика уровня обучаемости

Уровни усвоения учебного материала

Деятельность учащихся

Низкий уровень обучаемости

А (базовый уровень)

Репродуктивная деятельность

Средний уровень обучаемости

А; В (продвинутый уровень)

Реконструктивная деятельность

Высокий уровень обучаемости

А; В; С (творческий уровень)

Продуктивная деятельность

Разноуровневые задания облегчают организацию занятий в классе, создают условия для продвижения школьников в учебе в соответствии с их возможностями, создают в классе благоприятный психологический климат. У учащихся, в том числе и слабых, появляется уверенность в своих силах, они не чувствуют страха перед новыми задачами, рискуют пробовать свои силы в незнакомой ситуации, берутся за решение задач более высокого уровня. Это способствует активизации мыслительной деятельности учащихся, созданию положительной мотивации к учению. В результате такой деятельности школьники учатся самостоятельно добывать знания, у них развивается логическое мышление, умение составлять устный и письменный ответ на поставленный вопрос, анализировать ситуацию, высказывать свое мнение, применять полученные знания при решении задач, требующих творческого подхода.

За основу урока берётся одно общее задание - решение квадратного уравнения (изучалось в 8 классе), которое позволяет сэкономить время урока и помогает слабым ученикам в выполнении следующих заданий. Таблицы с теорией вывешиваются в классе, кроме того ученики получают алгоритмы выполнения заданий, которыми при необходимости могут воспользоваться. Примеры карт-алгоритмов: (приложение 1,приложение 2).

Выполнение любых заданий необходимо контролировать. При любом виде контроля ученик должен знать критерии оценок, поэтому данный вопрос обговаривается с учениками в начале урока. В ходе урока используются такие виды контроля, как самоконтроль и взаимоконтроль.

Проблемная ситуация создаётся постановкой перед учащимися проблемной задачи по решению биквадратного уравнения. Чтобы закрепить ситуацию успеха, учащимся предлагается дифференцированная домашняя работа.

Урок обобщения и систематизации знаний в 9 классе по теме по теме «Квадратичная функция».

Цели урока.

Образовательные: обобщить, систематизировать и углубить знания учащихся по теме «Квадратичная функция».

Развивающие: способствовать формированию умений применять приёмы сравнения, обобщения, выделения главного, переноса знаний в новую ситуацию; развитие творческих способностей учащихся.

Воспитательные: побуждать учеников к самоконтролю, взаимоконтролю, самоанализу учебной деятельности, воспитывать чувство коллективизма и ответственности за работу в группе.

Ход урока. Что есть лучшего? Сравнив прошедшее,

Свести его с настоящим.

К. Прутков.

1. Мотивационная беседа.

Тема «Квадратичная функция» - важная тема курса математики. Знание её необходимо как при дальнейшем изучении предмета, так и при решении заданий ГИА. На уроке мы обобщим и систематизируем знания по теме.

2. Актуализация знаний.

Задание 1.

Решите квадратное уравнение:

2х^{2 -} 3х -2 = 0

Ученики начинают самостоятельно решать задание в тетрадях, один человек выполняет задание на маркерной доске.

Ответ: х₁= -0,5; х₂=2.

Вопрос классу: Как можно выполнить проверку найденных корней ?

Ответ: по теореме Виета. В нашем случае: х₁∙ х_{2 =} -1,

х₁ + х₂ =1,5.

Если ученики не помнят теорему, то подстановкой найденных значений переменной в квадратное уравнение.

Квадратное уравнение мы решили, ответ проверили. Продолжим выполнение заданий в группах, используя при этом полученные нами результаты. Задания в каждой группе дифференцированные (каждый ученик имеет возможность выбора заданий). Оценка урока будет зависеть от уровня сложности выполненных учеником заданий. А - низкий уровень обученности, В - средний уровень обученности , С - высокий уровень обученности.

Задание 1 группе.

А). Разложить на множители квадратный трёхчлен 2х²-3х -2;

В). Разложить на множители квадратный трёхчлен -2х²+3х+2;

С). Сократить дробь

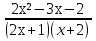
Задание 2 группе.

А). Решить методом интервалов неравенство 2х²- 3х -2 >0;

В). Решить методом интервалов неравенство -2х²+3х +2 > 0.

С). Решить методом интервалов неравенство ≥ 0.

Задание 3 группе.

А). Решить графически неравенство 2х²- 3х -2 > 0;

В). Записать графическое решение неравенства 2х² - 3х-2< 0;

С). Решить графически неравенство -2х² + 3х +2 ≥ 0.

Задание 4 группе.

А). Записать нули функции у = 2х² - 3х - 2; найти координаты точек пересечения графика функции с осью ординат;

В). Найти координаты вершины параболы у = 2х² - 3х - 2;

С). Построить в координатной плоскости график функции у = 2х² - 3х - 2.

На выполнение заданий отводится определённое время 10-15 минут. Учитель оказывает помощь слабым учащимся: консультирует, предлагает алгоритм решения задач, оказывает помощь в нахождении ошибок. Если сильный ученик справился с работой раньше других, он может помочь членам своей группы. После окончания данной работы представители от каждой группы объясняют решение своих заданий у доски.

Ученики других групп слушают, при необходимости кратко конспектируют и задают вопросы по ходу решения ( если им что-то неясно или с целью проверки знаний отвечающего).

Проведение физкультминутки.

3.Контроль и коррекция знаний.

Задание 2.

По графику, представленному группой 4, провести исследование функции

у= 2х² - 3х - 2

План исследования:

1. Область определения функции.

2. Область значений функции.

3. Нули функции.

4. Промежутки знакопостоянства.

5. Промежутки возрастания и убывания функции.

4. Проблемное задание.

Решите уравнение 2у⁴ - 3 у² - 2 = 0

5. Рефлексия. Подведение итогов работы группы и каждого ученика.

Результаты работы групп в течение урока можно заносить в таблицу:

группа

Быстрота выполнения заданий

Верные ответы

(А, В, С)

Вопросы других групп

Проблемное задание

Итог

1

2

3

4

Нарисуйте эскиз параболы у = 2х² - 3х -2 и дорисуйте лицо, которое соответствует вашему настроению по окончанию проделанной вами работы.

Вернёмся к эпиграфу урока. Как вы понимаете слова К. Пруткова? К сведению учеников, можно заметить, что К.Прутков - вымышленное имя. В 19 веке возникло литературное содружество, в которое входили А.К.Толстой и братья Жемчужниковы. Под выбранным псевдонимом, они создавали стихи и басни с социальными намёками, меткие афоризмы.

6. Домашнее задание.

На выбор:

1. Провести аналогичную работу с любым квадратным трёхчленом, выбранным в учебнике. Постараться выполнить хотя бы одно задание другой группы.

2.Решить графически уравнение 2х² - 3х - 2 = 0

3. Построить график функции у =│2х² - 3х - 2 │