Урок алгебры в 8 классе 'О любви к многоугольникам'

Название образовательного учреждения Муниципальное казенное образовательное учреждение

«Рогожинская основная общеобразовательная школа» городского округа город Михайловка

ФИО автора Колемаскина Наталия Александровна

Название интегрированных предметов математика и ИЗО.

Тема урока: "О любви к многоугольникам"

Класс 8 класс

Продолжительность занятия 80 минут

Тип урока: интегрированный урок

Применяемые технологии: технология развития критического мышления, ИКТ.

Цель урока: исследование видов многоугольников.

Задачи:

Обучающая задача: актуализировать, расширить и обобщить знания учащихся о многоугольниках; сформировать представление о "составных частях" многоугольника; провести исследование количества составных элементов правильных многоугольников (от треугольника до n - угольника).

Развивающая задача: развивать умения анализировать, сравнивать, делать выводы, развивать вычислительные навыки, устную и письменную математическую речь, память, а также самостоятельность в мышлении и учебной деятельности, умение работать в парах и группах; развивать исследовательскую и познавательную деятельность.

Воспитательная задача: воспитывать самостоятельность, активность, ответственность за порученное дело, упорство в достижении поставленной цели.

Оборудование: мультимедийная аппаратура, презентация урока, карточки с заданиями, шаблоны(правильные треугольники, шестиугольники и квадраты из расчета на каждого учащегося), тексты для маркировки, карточки с вопросами для работы в группах, образцы рукоделия в лоскутной технике, ножницы, листки клетчатой бумаги, краски, кисти.

Первое условие, которое надлежит выполнять в математике, - это быть точным,

второе - быть ясным и, насколько можно, простым. Л. Карно

Ход урока: Слайд 1

Окружающий нас мир - это мир геометрии.
А.Д. Александров

1.Стадия вызова-

Цели: - актуализация знаний учащихся по теме;

- мотивация каждого ученика к учебной деятельности.

Слайд 2. Отгадайте ребус:

-Сегодня на уроке речь пойдет о многоугольниках. Вашим домашним заданием было приготовить кластер о многоугольнике. Прошу его сейчас представить(проверка д/з).

Учащиеся представляют свои работы с комментариями, повторяют определения, свойства фигур, дополняют ответы друг друга.

Пример кластера одной из учениц: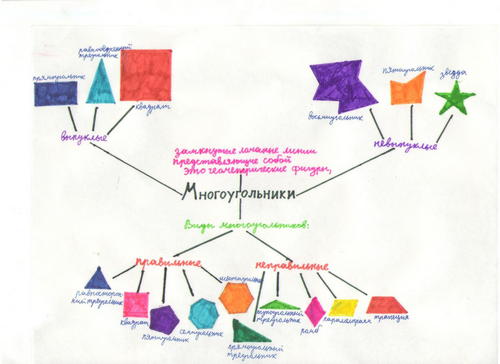

2. Стадия осмысления

Цель: -получение новой информации, ее осмысление, отбор,

-вызвать эмоциональный отклик на тему урока.

Прием: пометки на полях (Система маркировки текста «ИНСЕРТ» )

На стадии осмысления предлагается система маркировки текста (чтение с пометками), чтобы подразделить заключенную в нем информацию следующим образом:

• v (галочка) - этим знаком помечается информация, которая уже известна ученикам;

• - (минус) - помечается то, что противоречит их представлению;

• + (плюс) - помечается то, что является для них интересным и неожиданным;

• ? (вопросительный знак) ставиться, если что-то неясно, возникло желание узнать побольше.

Далее, читая текст, учащиеся помечают соответствующим значком на полях отдельные абзацы и предложения. После прочтения текста учащимся предлагается систематизировать информацию, расположив ее в соответствии со своими пометками в следующую таблицу: v - + ?

На стадии рефлексии происходит последовательное обсуждение каждой графы таблицы.

Формы работы: индивидуальная->групповая.

Каждому из группы выдается текст по теме урока, причем текст составлен таким образом, что он включает в себя как информацию уже известную учащимся, так и информацию абсолютно новую. Вместе с текстом учащиеся получают вопросы, ответы на которые необходимо в этом тексте найти.

Многоугольники. Виды многоугольников.

Кто не слышал о загадочном Бермудском треугольнике, в котором бесследно исчезают корабли и самолеты? А ведь знакомый нам с детства треугольник таит в себе немало интересного и загадочного.

Помимо уже известных нам видов треугольников, разделяемых по сторонам (разносторонний, равнобедренный, равносторонний) и углам (остроугольный, тупоугольный, прямоугольный) треугольник относится к большому семейству многоугольников, выделяемых среди множества различных геометрических фигур на плоскости.

Слово "многоугольник" указывает на то, что у всех фигур этого семейства "много углов". Но для характеристики фигуры этого не достаточно.

Ломаной А₁А₂…А_n называется фигура, которая состоит из точек А_1,А_2,…А_n и соединяющих их отрезков А₁А₂, А₂А₃,…. Точки называются вершинами ломаной, а отрезки звеньями ломаной. (рис.1)

Ломаная называется простой, если она не имеет самопересечений (рис.2,3).

Ломаная называется замкнутой, если у нее концы совпадают. Длиной ломаной называется сумма длин ее звеньев (рис.4).

Простая замкнутая ломаная называется многоугольником, если ее соседние звенья не лежат на одной прямой (рис.5)..

Вершины ломаной называются вершинами многоугольника, а звенья ломаной - сторонами многоугольника.

Многоугольник разбивает плоскость на две области: внутреннюю и внешнюю (рис.6).

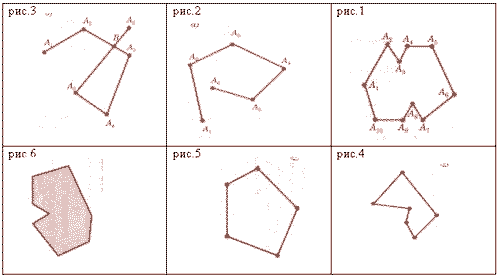
Отрезки, соединяющие не соседние вершины многоугольника, называются диагоналями.

Сумма углов выпуклого n - угольника равна 180⁰*(n - 2).

Выпуклый многоугольник называется правильным, если у него все стороны равны и все углы равны.

Так что квадрат можно назвать по-другому - правильным четырехугольником. Равносторонние треугольники также являются правильными. Такие фигуры давно интересовали мастеров, украшавших здания. Из них получались красивые узоры, например на паркете. Но не из всех правильных многоугольников можно было сложить паркет. Из правильных восьмиугольников паркет сложить нельзя. Дело в том, что у них каждый угол равен 135⁰.И если какая-нибудь точка является вершиной двух таких восьмиугольников, то на их долю придется 270⁰ , и третьему восьмиугольнику там поместиться негде: 360⁰ - 270⁰ =90⁰ .Но для квадрата этого достаточно. Поэтому можно сложить паркет из правильных восьмиугольников и квадратов.

Правильными бывают и звезды. Наша пятиконечная звезда - правильная пятиугольная звезда. А если повернуть квадрат вокруг центра на 45⁰ , то получится правильная восьмиугольная звезда.

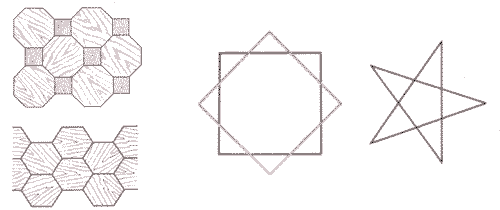
/Учащиеся работают с текстом, ищут ответы на поставленные вопросы, после чего формируются экспертные группы, работа в которых идет по одним и тем же вопросам: учащиеся выделяют главное, составляют опорный конспект, представляют информацию одной из графических форм. По окончании работы учащиеся возвращаются в свои рабочие группы./

Вопросы:

1 группа

Что называется ломаной? Объясните, что такое вершины и звенья ломаной.

Какая ломаная называется простой, замкнутой?

Что называется многоугольником? Что называется вершинами многоугольника, сторонами многоугольника?

2 группа

Что такое диагональ многоугольника?

Какой многоугольник называется выпуклым?

Объясните, какие углы многоугольника внешние, а какие внутренние?

3 группа

Какой многоугольник называется правильным? Приведите примеры правильных многоугольников.

Чему равна сумма углов выпуклого n-угольника?

Как найти количество всех диагоналей многоугольника?

Проблемная беседа

Учащимся предлагается найти применение правильным многоугольникам в жизни. Оценивается активность в беседе

-Вернемся к эпиграфу нашего урока: «Окружающий нас мир - это мир геометрии»
А.Д. Александров

-Что вы понимаете под этими словами?

- Где вы могли видеть правильные многоугольники? Слайд3

Слайд 4 1)Пчелиные соты

1. Состоят из множества шестигранных ячеек. Такое строение сот придает им необходимую прочность, кроме того, шестигранная форма ячеек требует наименьших затрат строительного материала (воска). На постройку одной пчелиной ячейки уходит около 13 мг воска, на постройку всего сота - 140-150 граммов.

2. То, что творит архитектор - пчела поистине уникально. Энергетическое строение Вселенной сегодня изучается квантовыми физиками, и оно идеально соответствует строению восковых сот.

3. А знаете ли Вы, что если на вощине сделать угол шестигранника на несколько тысячных радиан больше или меньше, то пчела сгрызет до основания этот участок и перестроит заново.

2) Сечение гайки, болта и многих технических деталей, карандашей имеет вид правильного шестиугольника.

3) Некоторые сложные молекулы углерода (например, графит) имеет гексагональную кристаллическую решетку.

Слайд 5-14 4) Паркет - это покрытие плоскости многоугольниками без пропусков и наложений.

- Из каких правильных многоугольников можно построить правильный паркет?

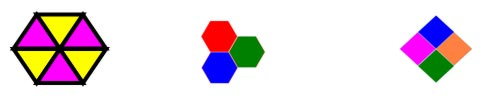
- Какое необходимое условие для построения паркета? (в узле 360 градусов)

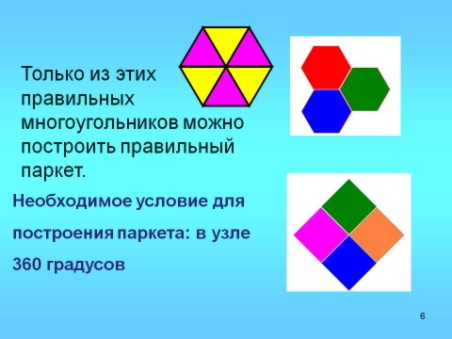
Слайд 15 5) Из лоскутков тканей можно изготовить своими руками покрывала, наволочки, коврики, одеяла

Динамическая физминутка

Паркеты Эшера и Пенроуза

- Приглядитесь, ребята: даже в нашем кабинете можно найти немало примеров паркетов. Учащиеся перечисляют (рисунок на линолеуме, потолочная плитка, рисунок на одежде…).

-Я хочу познакомить вас с удивительными художниками, которые даже в неочевидном видели очевидное. Это Морис Корнелиус Эшер и Ро́джер Пенроуз.

ЭШЕР Слайд 16-23

-Голландский художник Морис Корнелиус Эшер родился 17 июня 1898 года в Леевардене, в голландской провинции Фрисландия. Он был третьим сыном инженера Г. А. Эшера и его жены, дочери министра. С 1907 года Морис учится плотницкому делу и игре на пианино. В 1912-1918 годах он обучается в средней школе. Оценки по всем предметам у Мориса были плохими за исключением рисования. Учитель рисования заметил талант у мальчика и научил его делать гравюры по дереву. Практическ все произведения Мориса Эшера - это гравюры, выполненные на досках (в основном - груша) или спилах, поэтому его картины небольших размеров. Одними из первых его творений были паркет с ящерицами и голубями. Это искаженные базовые образцы стандартных мозаик в трехнаправленной симметрии и в шестинаправленной симметрии. Эшер не менее загадочен, чем его произведения с изображением замкнутой лестницы, идущей все время вверх, дома с невероятно переплетенными колоннами, мозаики, или как их называют - паркеты из повторяющихся фигур людей, животных или монстров - все это надо увидеть, чтобы понять, что это невозможно. А поняв, остаться в растерянности - ведь картины-то существуют! Интересно, что все вокруг воспринимали его, как гениального математика, а сам о себе он говорил следующее:

"Я так ни разу и не смог получить хорошей оценки по математике. Забавно, что я неожиданно оказался связанным с этой наукой. Поверьте, в школе я был очень плохим учеником. И вот теперь математики используют мои рисунки для иллюстрации своих книг. Представьте себе, эти ученые люди принимают меня в свою компанию как потерянного и вновь обретенного брата! Они, кажется, не подозревают, что математически я абсолютно безграмотен".

-посмотрите некоторые его работы. Казалось бы, как Эшер связан с многоугольниками? Математически доказано, что из всех правильных многоугольников регулярно разбивают плоскость только три из них: шестиугольник, квадрат и треугольник. Нерегулярных вариантов гораздо больше, например, во многих мозаиках используется пятиугольник. Эршер в своих эскизах использовал симметричные смещения многоугольников с поворотом и без, отражения.

Мы с Настей изобразили несколько примеров картин Эшера (демонстрация).

ПЕНРОУЗ Слайд 24-27

- Сэр Ро́джер Пенро́уз родился живет и здравствует по сей день (, ) - английский , активно работающий в различных областях . В 1973 году английский математик Роджер Пенроуз создал особенную мозаику из геометрических фигур, которая так и стала называться - мозаикой Пенроуза.
Мозаика Пенроуза представляет собой узор, собранный из многоугольных плиток двух определённых форм (немного различающихся ромбов). Ими можно замостить бесконечную плоскость без пробелов.

Получающееся изображение выглядит так, будто является неким "ритмическим" орнаментом - картинкой, обладающей трансляционной симметрией. Такой тип симметрии означает, что в узоре можно выбрать определённый кусочек, который можно "копировать" на плоскости, а затем совмещать эти "дубликаты" друг с другом параллельным переносом (проще говоря, без поворота и без увеличения).

Однако, если присмотреться, можно узреть, что в узоре Пенроуза нет таких повторяющихся структур - он апериодичен. Но дело отнюдь не в оптическом обмане, а в том, что мозаика не хаотична: она обладает вращательной симметрией пятого порядка.

Это значит, что изображение можно поворачивать на минимальный угол, равный 360 / n градусам, где n - порядок симметрии, в данном случае n = 5. Следовательно, угол поворота, который ничего не меняет, должен быть кратен 360 / 5 = 72 градусам.

Примерно десятилетие выдумка Пенроуза считалась не более чем милой математической абстракцией. Однако в 1984 году Дэн Шехтман профессор израильского технологического института, занимаясь изучением строения алюминиево-магниевого сплава, обнаружил, что на атомной решётке этого вещества происходит дифракция.

Предыдущие представления, существовавшие в физике твёрдого тела, исключали такую возможность: структура дифракционной картины обладает симметрией пятого порядка. Её части нельзя совмещать параллельным переносом, а значит, это вовсе никакой не кристалл. Но дифракция характерна как раз для кристаллической решётки! Учёные договорились о том, что данный вариант будет назваться квазикристаллами - чем-то вроде особого состояния вещества. Ну а вся красота открытия в том, что для него уже давно была готова математическая модель - мозаика Пенроуза.

А совсем недавно стало понятно, что этой математической конструкции намного больше лет, чем можно было себе представить. В 2007 году Питер Лу , физик из Гарварда за компанию с другим физиком - Полом Стейнхардтом но из Принстона - опубликовал в Science статью, посвящённую мозаикам Пенроуза . Казалось бы, неожиданного тут немного: открытие квазикристаллов привлекло живой интерес к данной теме, что привело к появлению кучи публикаций в научной прессе.

Однако изюминка работы в том, что она посвящена далеко не современной науке. Да и вообще - не науке. Питер Лу обратил внимание на узоры, покрывающие мечети в Азии, построенные ещё в Средневековье. Эти легко узнаваемые рисунки сделаны из мозаичной плитки. Они называются гирихи (от арабского слова "узел") и представляют собой геометрический орнамент, характерный для исламского искусства и состоящий из многоугольных фигур. Образец выкладки плитки, показанный в арабском манускрипте XV века. Цветами исследователи выделили повторяющиеся области. На основе этих пяти элементов выстроены все геометрические узоры средневековых арабских мастеров. Повторяющиеся элементы не обязательно совпадают с границами плиток.

В исламском орнаменте выделяют два стиля: геометрический - гирих, и растительный - ислими.
Гирих (перс.) - сложный геометрический орнамент, составленный из стилизованных в прямоугольные и полигональные фигуры линий. В большинстве случаев используется для внешнего оформления мечетей и книг в крупном издании.
Ислими (перс.) - вид орнамента, построенного на соединении вьюнка и спирали. Воплощает в стилизованной или натуралистической форме идею непрерывно развивающегося цветущего лиственного побега и включает в себя бесконечное разнообразие вариантов. Наибольшее распространение он получил в одежде, книгах, внутренней отделке мечетей, посуде.
Обложка Корана 1306-1315 годов и прорисовка геометрических фрагментов,
на которых основан узор. Этот и следующий примеры не соответствуют
решёткам Пенроуза, но обладают вращательной симметрией пятого порядка

До открытия Питера Лу считалось, что древние архитекторы создавали узоры гириха c помощью линейки и циркуля (если вообще не по наитию). Однако пару лет назад, находясь во время путешествия в Узбекистане, Лу заинтересовался узорами мозаик, украшавшими местную средневековую архитектуру, и приметил в них что-то знакомое. Вернувшись в Гарвард, учёный стал рассматривать аналогичные мотивы в мозаиках на стенах средневековых построек Афганистана, Ирана, Ирака и Турции.
Этот образец датирован более поздним периодом - 1622 год (индийская мечеть).

Питер Лу обнаружил, что геометрические схемы гирихов практически одинаковы, и смог выделить основные элементы, использовавшихся во всех геометрических орнаментах. Кроме того, он нашёл чертежи этих изображений в старинных манускриптах, которыми древние художники пользовались в качестве своеобразной шпаргалки по украшению стен.
Для создания этих узоров применяли не простые, случайно придуманные контуры, а фигуры, которые были расположены в определённом порядке. Древние узоры оказались точными построениями мозаик Пенроуза!

В исламской традиции существовал строгий запрет на изображение людей и животных, поэтому в оформлении зданий большую популярность приобрёл геометрический орнамент. Средневековые мастера умудрялись как-то делать его разнообразным. Но в чём был секрет их "стратегии" - никто не знал. Так вот, секрет как раз оказывается в использовании специальных мозаик, которые могут, оставаясь симметричными, заполнять плоскость, не повторяясь.

Другой "фокус" этих изображений в том, что, "копируя" такие схемы в различных храмах по чертежам, художники неизбежно должны были бы допустить искажения. Но нарушения данного характера минимальны. Объясняется это только тем, что в масштабных чертежах смысла не была: главное - принцип, по которому строить картину.

Для сборки гирихов применяли плитки пяти видов (десяти- и пятиугольные ромбы и "бабочки"), которые в мозаике составлялись, прилегая друг к другу без свободного пространства между ними. Мозаики созданные из них, могли обладать как сразу вращательной и трансляционной симметрией, так и только вращательной симметрией пятого порядка (то есть являлись мозаиками Пенроуза).
Фрагмент орнамента иранского мавзолея 1304 года. Справа - реконструкция гирихов

Исследовав сотни фотографий средневековых мусульманских достопримечательностей, Лу со Стейнхардтом смогли датировать появление подобной тенденции XIII веком. Постепенно этот способ приобретал всё большую популярность и к XV веку стал широко распространённым. Датировка примерно совпадает с периодом развития техники декорирования дворцов, мечетей, различных важных зданий глазурованной цветной керамической плиткой в форме различных многоугольников. То есть керамическую плитку специальных форм создавали именно для гирихов.

Образцом почти идеальной квазикристаллической структуры исследователи посчитали святилище имама Дарб-и в иранском городе Исфахане, датируемое 1453 годом.
Портал святилища имама Дарб-и в Исфахане (Иран).
Здесь друг на друга наложены сразу две системы гирихов.
Теперь остается найти ответы на ряд загадок в истории гириха и мозаик Пенроуза. Каким образом и для чего древние математики открыли квазикристаллические структуры? Придавали ли средневековые арабы мозаикам какой-то иной смысл, кроме художественного? Почему столь интересная математическая концепция была забыта на полтысячелетия? И самое интересное - какие еще современные открытия являются новым, которое на самом деле - хорошо забытое старое?

Слайд 28

- Слава великих художников увековечена в памятнике (в честь Пенроуза) и медали (в честь Эшера).

Физминутка для глаз

3.Стадия рефлексии-

Цель: - убедить в важности осознанного видения межпредметных связей;

- развить творческие способности;

- оценка своих знаний, вызов к следующему шагу познания;

- осмысление и присвоение полученной информации .

Прием: исследовательская работа.

Формы работы: индивидуальная->парная->групповая.

В рабочих группах оказываются специалисты по ответам на каждый из разделов предложенных вопросов.

Вернувшись в рабочую группу, эксперт знакомит других членов группы с ответами на свои вопросы. В группе происходит обмен информацией всех участников рабочей группы. Таким образом, в каждой рабочей группе, благодаря работе экспертов, складывается общее представление по изучаемой теме.

Слайд 29 Решение интересных задач по теме урока.

• В четырехугольнике, проведите прямую так, чтобы она разделила его на три треугольника.

• Сколько сторон имеет правильный многоугольник, каждый из внутренних углов которого равен 135⁰?

• В некотором многоугольнике все внутренние углы равны между собой. Может ли сумма внутренних углов этого многоугольника равняться: 360⁰, 380⁰?

• У вас на партах приготовлены круги и ножницы. Вырежьте из них правильные четырехугольники, правильные треугольники, правильные шестиугольники.

• Составьте свой паркет.

резерв

Знакомство с построением паркетов на клетчатой бумаге. Изображение своих моделей паркетов с помощью шаблонов и простейших геометрических фигур.

Подведение итогов урока.

Мини выставка работ.

Слайд 30

- Мы повторили _________;
- Мы закрепили умения _________;
- Теперь я могу _______________.

Синквейн Слайд 31

Создание синквейна - стихотворения из 5 строк (от французского «5»), которое строится по следующим правилам:

1. в первой строчке тема называется одним словом (обычно существительным);

2. во второй строчке дается описание темы в двух словах (два прилагательных);

3. в третьей строчке дается описание действия в рамках данной темы тремя словами(2 глагола);

4. в четвертой строке - фраза из четырех слов, показывающая отношение к теме;

5. в пятой строке - повторение сути темы другим словом на эмоциональном или философско-обобщенном уровне.

Домашнее задание: Слайд 32

1. Изготовить узор, паркет, др. из правильных многоугольников.

2.Исследовательская работа учащихся - заполнение таблицы.

Правильные многоугольники

Чертеж

Кол-во сто

рон

Кол-во вершин

Сумма всех внутр.углов

Градусная мера внутр.угла

Градусная мера

внешн.угла

Кол-во диагона

лей

А)треугольник

Б) четырех-угольник

В)пятиуольник

Г) шестиугольник

Д) n-угольник

Источники:

9. http://ppt4web.ru/geometrija/geometricheskie-preobrazovanija-i-parkety.html

10. Библиотечка журнала «Математика в школе. Паркеты»

11. А.С. Питерских, Г.Е.Гуров. Изобразительное искусство. Дизайн и архитектура в жизни человека: Учеб. для 7-8- кл. общеобразоват. Учреждений /Под ред. Б. М. Неменского. - М.:Просвещение, 2008.

12. Волошинов А. В. Математика и искусство. - М.: Просвещение, 2000.

13. Орнамент всех времен и стилей - М.: Арт - Родник, 1997.

14. Колякина В.И. Методика организации уроков коллективного творчества: Планы и сценарии уроков ИЗО. - М.:Владос, 20004.

15. М. Эшер - Арт - Родник, изд. на русском языке, 2000.