- Учителю
- Дипломная работа на тему: «Определение основных элементарных функций с помощью функциональных уравнений»
Дипломная работа на тему: «Определение основных элементарных функций с помощью функциональных уравнений»
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ТАМБОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИМЕНИ Г.Р. ДЕРЖАВИНА»
Институт математики, физики и информатики
Кафедра функционального анализа
Допущена к защите
Заведующий кафедрой
________Молчанов В.Ф.
«___»____________2015г.
Стерликова Марина Игоревна
«Определение основных элементарных функций с помощью функциональных уравнений»
Дипломная работа
Студентки 6 курса
направления подготовки
050101.65 математика
заочной формы обучения
______________ Стерликовой М.И.
Руководитель:
к. ф.-м. н., доцент кафедры функционального анализа
Фомичева Юлия Геннадьевна
_____________ Фомичева Ю.Г.
Тамбов 2015
Реферат
Стерликова М.И. Определение основных элементарных функций с помощью функциональных уравнений: выпускная квалификационная работа/ Стерликова Марина Игоревна; Тамбовский государственный университет имени Г.Р.Державина, институт математики физики и информатики, кафедра алгебры и геометрии.- Тамбов, 2015.- 40с.
Ключевые слова: функциональные уравнения, методы решения функциональных уравнений, элементарные функции, уравнения Коши.
Цель выпускной квалификационной работы: изучить функциональные уравнения и применение этих уравнений к определению элементарных функций: линейной, показательной, логарифмической, степенной и тригонометрических функций.
Методы: анализ, исследование
Аннотация: Данная работа выполнена на основе анализа учебно-практических пособий. В работе рассмотрены основные вопросы о функциональных уравнениях, методы решения функциональных уравнений. Приведенные примеры и задачи позволяют успешно овладеть знаниями по изучаемой дисциплине. Вопросы, рассмотренные в работе, не только расширяют кругозор, но и несут обучающую функцию, что только подчеркивает значимость выбранной темы.
Введение
Функциональными уравнениями занимаются с очень давних пор, этому курсу так и не нашлось достойного места в математических программах. А жаль. Ведь решение отдельных функциональных уравнений требует достаточно глубокого понимания предмета и прививает любовь к самостоятельной творческой работе.
В настоящее время содержания различных олимпиад - от школьных и
городских до международных - стали включать так называемые
функциональные уравнения и неравенства. Даже прослеживается идея
привлечения таких уравнений и неравенств к содержанию вступительных
экзаменов в высшие учебные заведения на разные факультеты.
Следовательно, желающих научиться решать такого рода задачи
становится больше. Поэтому с уверенностью можно утверждать, что
тема «Функциональные уравнения» на сегодня является вполне
актуальной.
В настоящее время практически нет пособий, обучающих решению
функциональных уравнений. Поэтому ощущается потребность в пособии,
которое на простых и конкретных примерах способно показать весь
арсенал современных методов решения функциональных уравнений. В
нашей выпускной квалификационной работе мы постараемся решить эту
задачу.
Цель выпускной квалификационной работы: изучить функциональные уравнения и применение этих уравнений к определению элементарных функций: линейной, показательной, логарифмической, степенной и тригонометрических функций.
Задачи:
- изучить научно практическую литературу по теме выпускной квалификационной работы,
- рассмотреть функциональные уравнения,
- раскрыть методы решения функциональных уравнений,
- составить функциональные уравнения соответствующие элементарным функциям,
- развитие интереса к решению нестандартных математических задач и математики в целом.
При написании работы было изучено, проанализировано 4 источника.
Выпускная квалификационная работа состоит из двух глав.
В первой главе рассмотрим методы решения функциональных уравнений: метод сведения функционального уравнения к известному уравнению с помощью замены переменной и функции, метод подстановок, применение элементов математического анализа к решению функциональных уравнений; для каждого метода подобраны примеры по решению уравнений.
Во второй главе представим определение основных элементарных
функций (![]() ,
,![]() ,
,
![]() ,
, ![]() ,
, ![]() ) с помощью функциональных уравнений, а так же рассмотрели
некоторые их свойства.
) с помощью функциональных уравнений, а так же рассмотрели
некоторые их свойства.
Вопросы, рассмотренные в работе, не только расширяют кругозор, но и несут обучающую функцию, что только подчеркивает значимость выбранной темы.
История развития функциональных уравнений
Под функциональным уравнением в узком смысле слова понимают уравнение, неизвестная функция которого связана с известными функциями одной или нескольких переменных при помощи образования сложной функции (композиции).
Например: ![]() , где
, где ![]() -неизвестная функция,
-неизвестная функция, ![]() и
и ![]() - независимые переменные.
- независимые переменные.
Некоторые функциональные уравнения знакомы нам еще из школьного
курса это![]() ,
,
![]() ,
, ![]() , которые задают такие свойства функций, как чётность,
нечётность, периодичность.
, которые задают такие свойства функций, как чётность,
нечётность, периодичность.
Решением функционального уравнения на множестве ![]() называется функция, при подстановке которой в функциональное
уравнение оно превращается в верное равенство на множестве
называется функция, при подстановке которой в функциональное
уравнение оно превращается в верное равенство на множестве![]() .
.
Например: Покажем, что функция ![]() является решением функционального уравнения
является решением функционального уравнения ![]() .
.
Действительно, ![]()
![]() для всех x и y. Поэтому функция
для всех x и y. Поэтому функция ![]() является решением функционального уравнения
является решением функционального уравнения ![]() . Задача решения функциональных уравнений является одной из самых
старых в математическом анализе. Они появились почти одновременно с
зачатками теории функций. Первый настоящий расцвет этой дисциплины
связан с проблемой параллелограмма сил. Еще в 1769 году Даламбер
свел обоснование закона сложения сил к решению функционального
уравнения
. Задача решения функциональных уравнений является одной из самых
старых в математическом анализе. Они появились почти одновременно с
зачатками теории функций. Первый настоящий расцвет этой дисциплины
связан с проблемой параллелограмма сил. Еще в 1769 году Даламбер
свел обоснование закона сложения сил к решению функционального
уравнения
![]() (1)
(1)
То же уравнение с той же целью было рассмотрено Пуассоном в 1804
году при некотором предположении аналитичности, между тем как в
1821 году Коши (1789 - 1857) нашел общие решения этого уравнения
![]() ,
, ![]() ,
, ![]() , предполагая только непрерывность
, предполагая только непрерывность ![]() .
.
Даже известная формула неевклидовой геометрии для угла
параллельности ![]() была получена Н.И. Лобачевским (1792 - 1856) из функционального
уравнения
была получена Н.И. Лобачевским (1792 - 1856) из функционального
уравнения
![]() (2)
(2)
![]()
![]() которое
он решил методом, аналогичным методу Коши.
которое
он решил методом, аналогичным методу Коши.
Ряд геометрических задач, приводящих к функциональным
уравнениям, рассматривал английский математик Ч. Баббедж (1792
-1871). Он изучал периодические кривые второго порядка,
определяемые следующим свойством для любой пары точек кривой: если
абсцисса второй точки равна ординате первой, то ордината второй
точки равна абсциссе первой. Пусть такая кривая является графиком
функции ![]() - произвольная ее точка. Тогда, согласно условию, точка с абсциссой
- произвольная ее точка. Тогда, согласно условию, точка с абсциссой
![]() имеет ординату х. Следовательно,
имеет ординату х. Следовательно,
![]() (3)
(3)
Функциональному уравнению (3) удовлетворяют функции: ![]() ,
, ![]()
Одними из простейших функциональных уравнений являются уравнения Коши
![]() ,
(4)
,
(4)
![]() ,
(5)
,
(5)
![]() ,
(6)
,
(6)
![]() .
(7)
.
(7)
Эти уравнения Коши подробно изучил в своем курсе анализа,
изданном в 1821 году. Непрерывные решения этих четырех основных
уравнений имеют соответственно вид ![]() .
.
В классе разрывных функций могут быть и другие решения. Уравнение (4) ранее рассматривалось Лежандром и Гауссом при выводе основной теоремы проективной геометрии и при исследовании гауссовского закона распределения вероятностей.
Функциональное уравнение (4) было опять применено Г. Дарбу к
проблеме параллелограмма сил и к основной теореме проективной
геометрии; его главное достижение - значительное ослабление
предположений. Мы знаем, что функциональное уравнение Коши (4)
характеризует в классе непрерывных функций линейную однородную
функцию ![]() . Дарбу же показал, что всякое решение, непрерывное хотя бы в
одной точке или же ограниченное сверху (или снизу) в произвольно
малом интервале, также должно иметь вид
. Дарбу же показал, что всякое решение, непрерывное хотя бы в
одной точке или же ограниченное сверху (или снизу) в произвольно
малом интервале, также должно иметь вид ![]() . Дальнейшие результаты по ослаблению предположений следовали
быстро один за другим (интегрируемость, измеримость на множестве
положительной меры и даже мажорируемость измеримой функцией).
Возникает вопрос: существует ли хоть одна какая-нибудь аддитивная
функция (т. е. удовлетворяющая (4)), отличная от линейной
однородной. Найти такую функцию действительно нелегко! В ходе
работы мы покажем, что при рациональных x значения любой аддитивной
функции должны совпадать со значениями некоторой линейной
однородной функции, т. е.
. Дальнейшие результаты по ослаблению предположений следовали
быстро один за другим (интегрируемость, измеримость на множестве
положительной меры и даже мажорируемость измеримой функцией).
Возникает вопрос: существует ли хоть одна какая-нибудь аддитивная
функция (т. е. удовлетворяющая (4)), отличная от линейной
однородной. Найти такую функцию действительно нелегко! В ходе
работы мы покажем, что при рациональных x значения любой аддитивной
функции должны совпадать со значениями некоторой линейной
однородной функции, т. е. ![]() для
для ![]() . Казалось бы, что тогда
. Казалось бы, что тогда ![]() для всех действительных
для всех действительных ![]() . Если
. Если ![]() - непрерывна, то это действительно так, если же данное
предположение отбросить - то нет. Первый пример отличного от
- непрерывна, то это действительно так, если же данное
предположение отбросить - то нет. Первый пример отличного от
![]() разрывного решения функционального уравнения (4) построил в 1905
году немецкий математик Г. Гамель с помощью введённого им базиса
действительных чисел.
разрывного решения функционального уравнения (4) построил в 1905
году немецкий математик Г. Гамель с помощью введённого им базиса
действительных чисел.
Многие функциональные уравнения не определяют конкретную
функцию, а задают широкий класс функций, т. е. выражают свойство,
характеризующее тот или иной класс функций. Например,
функциональное уравнение ![]() характеризует класс функций, имеющих период 1, а уравнение
характеризует класс функций, имеющих период 1, а уравнение
![]() - класс функций, симметричных относительно прямой
- класс функций, симметричных относительно прямой![]() ,
и т. д.
,
и т. д.
Вообще, для функциональных уравнений, не сводящихся к дифференциальным или интегральным, известно мало общих методов решения. Отсюда возникает необходимость рассмотреть вопрос о методах решения функциональных уравнений.
1. Методы решения функциональных уравнений
1.1 Метод сведения функционального уравнения к известному уравнению с помощью замены переменной и функции
Рассмотрим определённые типы функциональных уравнений, которые можно свести к уравнениям, общие решения которых мы уже знаем. Как правило, такие уравнения сводятся к основным уравнениям Коши (4) - (7). Метод основан на введении вспомогательной функции, которую следует подобрать таким образом, чтобы после преобразований было ясно, что она удовлетворяет одному из известных функциональных уравнений.
Пример 1. Найти все непрерывные функции ![]() , определенные на промежутке
, определенные на промежутке![]() ,
для которых разность
,
для которых разность ![]() при произвольных допустимых значениях
при произвольных допустимых значениях ![]() и
и ![]() не зависит от
не зависит от ![]() .
.
Решение. По условию, выражение ![]() не зависит от
не зависит от![]() ,
поэтому
,
поэтому ![]() .
.
Положив ![]() , получим функциональное уравнение Коши
, получим функциональное уравнение Коши ![]() .
.
Известно, что в классе непрерывных функций ![]() . Отсюда
. Отсюда ![]() , где
, где ![]() . Проверка показывает, что условию задачи удовлетворяют функции
. Проверка показывает, что условию задачи удовлетворяют функции
![]() при произвольных
при произвольных ![]() и
и ![]() .
.
Рассмотрим пример, считая ![]() и
и ![]() различными фиксированными числами. Так как
различными фиксированными числами. Так как ![]() не зависит от
не зависит от ![]() , то
, то ![]() . Пусть
. Пусть![]() ,
тогда
,
тогда ![]() , где
, где ![]() ,
, ![]() - постоянная. Заменив
- постоянная. Заменив ![]() на
на ![]() , получим
, получим ![]() .
.
Вычитая из обеих частей ![]() , получим
, получим![]() ,
или
,
или ![]()
![]() ,
(8)
,
(8)
где ![]() .
.
Уравнению (8) удовлетворяют периодические с периодом ![]() функции. Отсюда
функции. Отсюда ![]() .
.
При проверке убеждаемся, что функции вида ![]() где
где ![]() - произвольная константа, а
- произвольная константа, а![]() -
непрерывная периодическая с периодом
-
непрерывная периодическая с периодом ![]() функция, обладают требуемым свойством.
функция, обладают требуемым свойством.
Пример 2. Известно, что сложение действительных чисел обладает
сочетательным свойством: ![]()
для любых ![]() . Требуется найти все непрерывные функции
. Требуется найти все непрерывные функции ![]() , «сохраняющие» сочетательность, т. е.
, «сохраняющие» сочетательность, т. е.
![]() (9)
(9)
Решение. Перепишем (9) в виде ![]() .
.
Легко видеть, что левая часть не зависит от х, т. е. ![]() .
.
При ![]() имеем
имеем ![]() . Пришли к функциональному уравнению Коши (4)
. Пришли к функциональному уравнению Коши (4) ![]() . Его непрерывным решением являются функции
. Его непрерывным решением являются функции ![]() . Таким образом,
. Таким образом, ![]() , где
, где ![]() и
и ![]() - произвольные константы.
- произвольные константы.
Пример 3. Найти плоские кривые, обладающие следующим свойством: для произвольных двух точек сумма произведений абсциссы одной точки на ординату другой равна ординате точки, абсцисса которой равна произведению абсцисс данных точек.
Решение. Ограничимся отысканием кривых, являющихся графиками непрерывных функций, определенных при положительных значениях аргумента.
Задача сводится к решению функционального уравнения ![]()
Пусть ![]() . Тогда получим уравнение Коши (6) вида
. Тогда получим уравнение Коши (6) вида ![]() . Так как
. Так как ![]() непрерывна при
непрерывна при![]() ,
то
,
то![]() .
Отсюда
.
Отсюда ![]() с произвольной константой
с произвольной константой ![]() .
.
Пример 4. Найти непрерывные решения функционального уравнения
![]() .
.![]()
Решение. В качестве вспомогательной функции здесь удобно считать
следующую функцию: ![]() . Тогда подставляя в исходное уравнение
. Тогда подставляя в исходное уравнение ![]() , получим
, получим ![]() ,
, ![]() .
.
Это уравнение Коши его решением является функция ![]() . Окончательно находим
. Окончательно находим ![]() и все такие функции удовлетворяют условию.
и все такие функции удовлетворяют условию.
Пример 5. Решить уравнение Йенсена в классе непрерывных функций
![]() .
.
Решение. Положим в уравнении ![]() вместо
вместо ![]() и 0 вместо
и 0 вместо ![]() , получим:
, получим: ![]() . Сравнивая полученное соотношение с первоначальным функциональным
уравнением, имеем:
. Сравнивая полученное соотношение с первоначальным функциональным
уравнением, имеем: ![]() . Это уравнение переходит в уравнение Коши (4) при подстановке
. Это уравнение переходит в уравнение Коши (4) при подстановке
![]() , тогда
, тогда ![]() , а это решение действительно удовлетворяет уравнению Йенсена.
, а это решение действительно удовлетворяет уравнению Йенсена.
Пример 6. Найти все непрерывные функции ![]() , удовлетворяющие тождеству
, удовлетворяющие тождеству ![]() .
.
Решение. Поделив тождество на ![]() , перепишем его так:
, перепишем его так: ![]() , отсюда ясно, что в качестве вспомогательной нужно взять функцию:
, отсюда ясно, что в качестве вспомогательной нужно взять функцию:
![]() . Тогда функция
. Тогда функция ![]() удовлетворяет (6). Поэтому находим
удовлетворяет (6). Поэтому находим ![]() .
.
1.2 Метод подстановок
Заменяя некоторые переменные функционального уравнения либо конкретными значениями, либо какими-либо другими выражениями пытаемся либо упростить это уравнение, либо привести его к такому виду, что дальнейшее решение станет очевидным. Особенность применяемого метода как раз и состоит в том, что в ряде случаев он позволяет отыскать решения в классе всевозможных функций. Поясним метод на следующих примерах.
Пример 7. Найти все решения функционального уравнения ![]() .
.
Решение. Положим в уравнении ![]() . Так как
. Так как ![]() - произвольно, то
- произвольно, то ![]() .
.
Пусть теперь![]() .
Подставим в уравнение
.
Подставим в уравнение ![]() , получим:
, получим: ![]() или
или ![]() . Функция
. Функция ![]() является решением исходного уравнения.
является решением исходного уравнения.
Пример 8. Пусть ![]() - некоторое действительное число. Найти функцию
- некоторое действительное число. Найти функцию ![]() , определённую для всех
, определённую для всех ![]() и удовлетворяющую уравнению
и удовлетворяющую уравнению ![]() , где
, где ![]() - заданная функция, определённая при
- заданная функция, определённая при ![]() .
.
Решение. При замене ![]() получаем систему
получаем систему 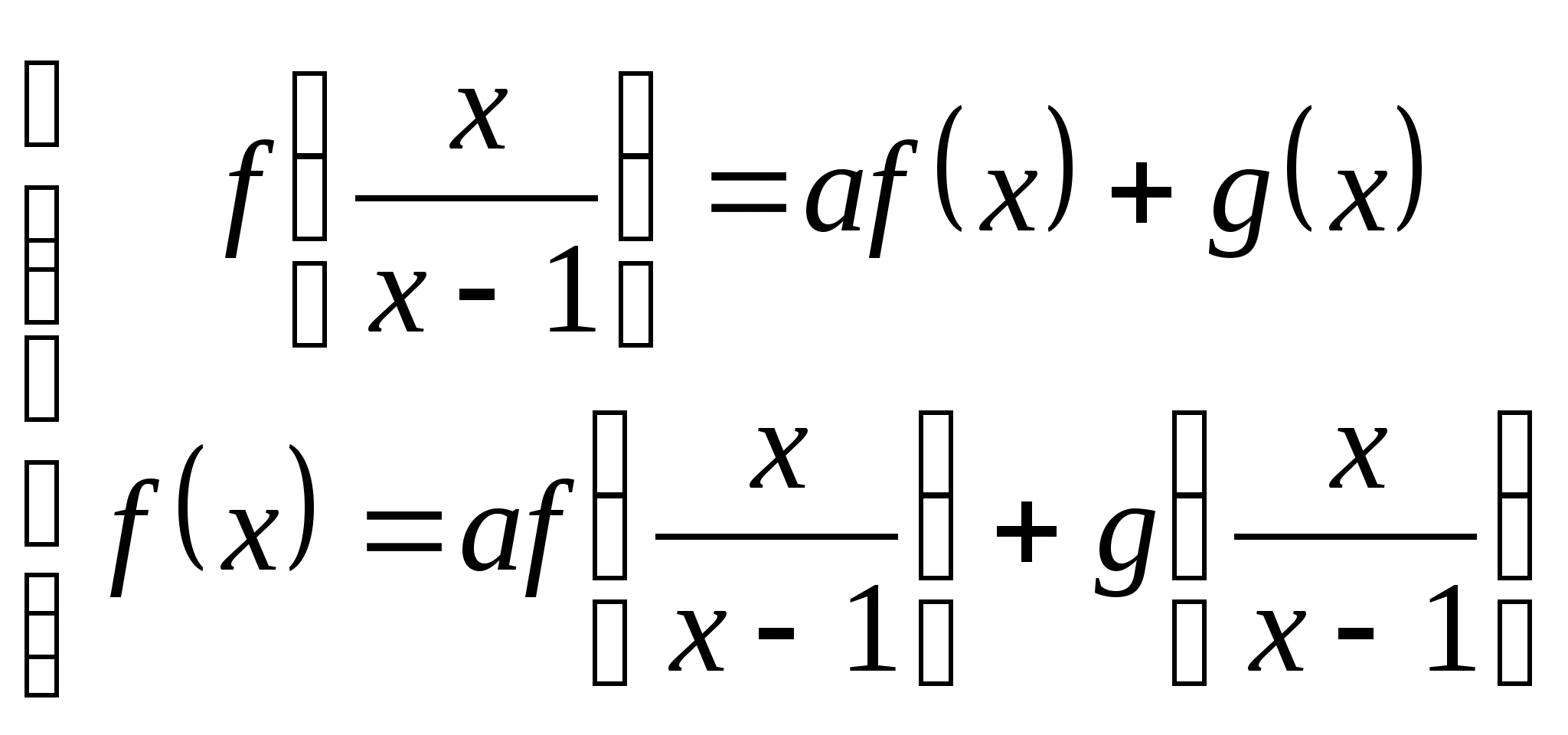 ,
,
решением которой при ![]() является функция
является функция 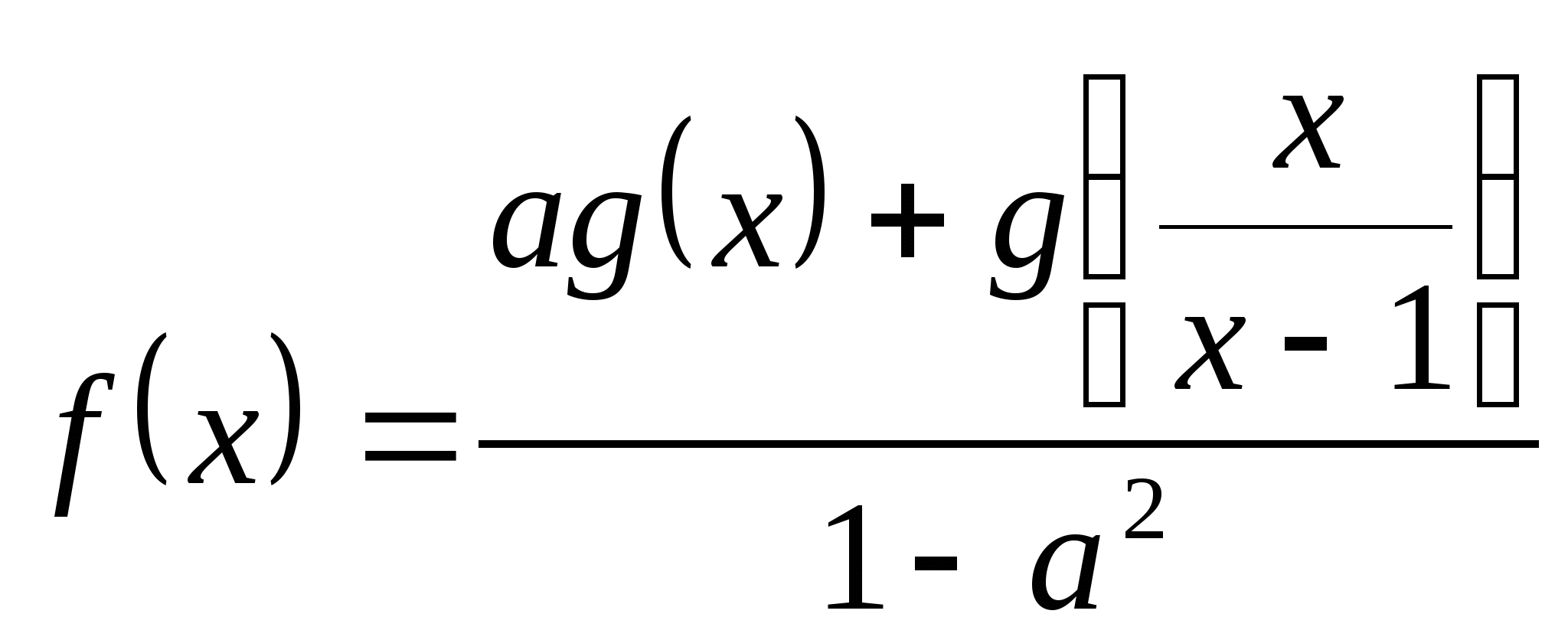 .
.
Пример 9. Найти все функции ![]() , заданные на промежутке
, заданные на промежутке ![]() , для которых выполнено равенство
, для которых выполнено равенство ![]() .
.
Решение. Выполнив последовательно две замены ![]() ,
, ![]() ,
,
приходим к системе функциональных уравнений: 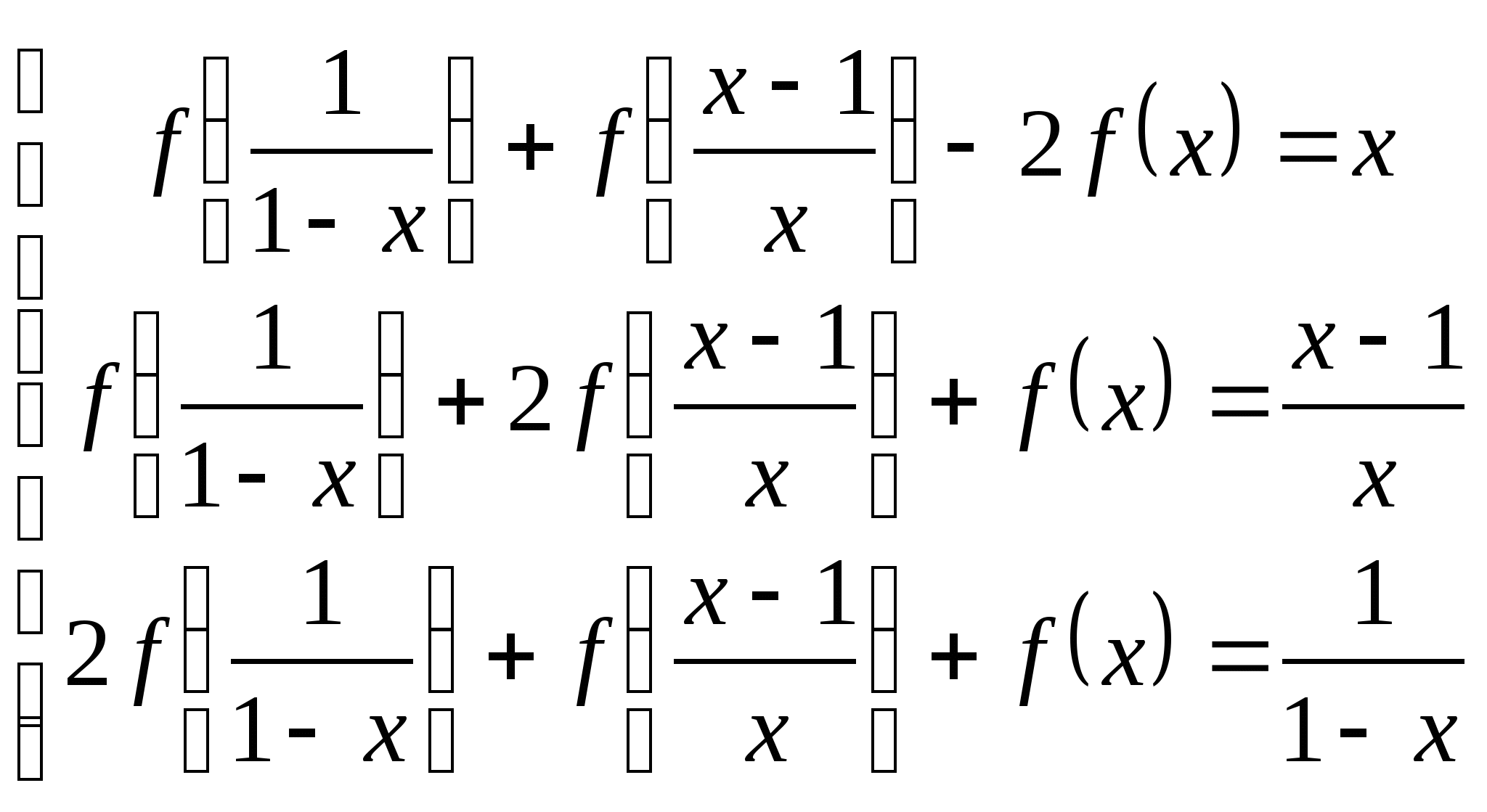 .
.
Последнее уравнение есть сумма первых двух, умноженных на -1, т.
е. из данной системы функция ![]() однозначно не определяется. Из первых двух уравнений находим
однозначно не определяется. Из первых двух уравнений находим
![]() ,
, ![]() . Мы можем определить
. Мы можем определить ![]() произвольным образом на одном из интервалов
произвольным образом на одном из интервалов ![]() и эти формулы дадут нам расширение
и эти формулы дадут нам расширение ![]() на все множество
на все множество ![]() .
.
Пример 10. Найти решение системы функциональных уравнений
относительно неизвестных функций ![]() и
и![]() :
:

Решение. В первом уравнении сделаем подстановку ![]() . При этом
. При этом ![]() и первое уравнение принимает вид:
и первое уравнение принимает вид: ![]() или
или ![]() . В результате получаем систему уравнений:
. В результате получаем систему уравнений: 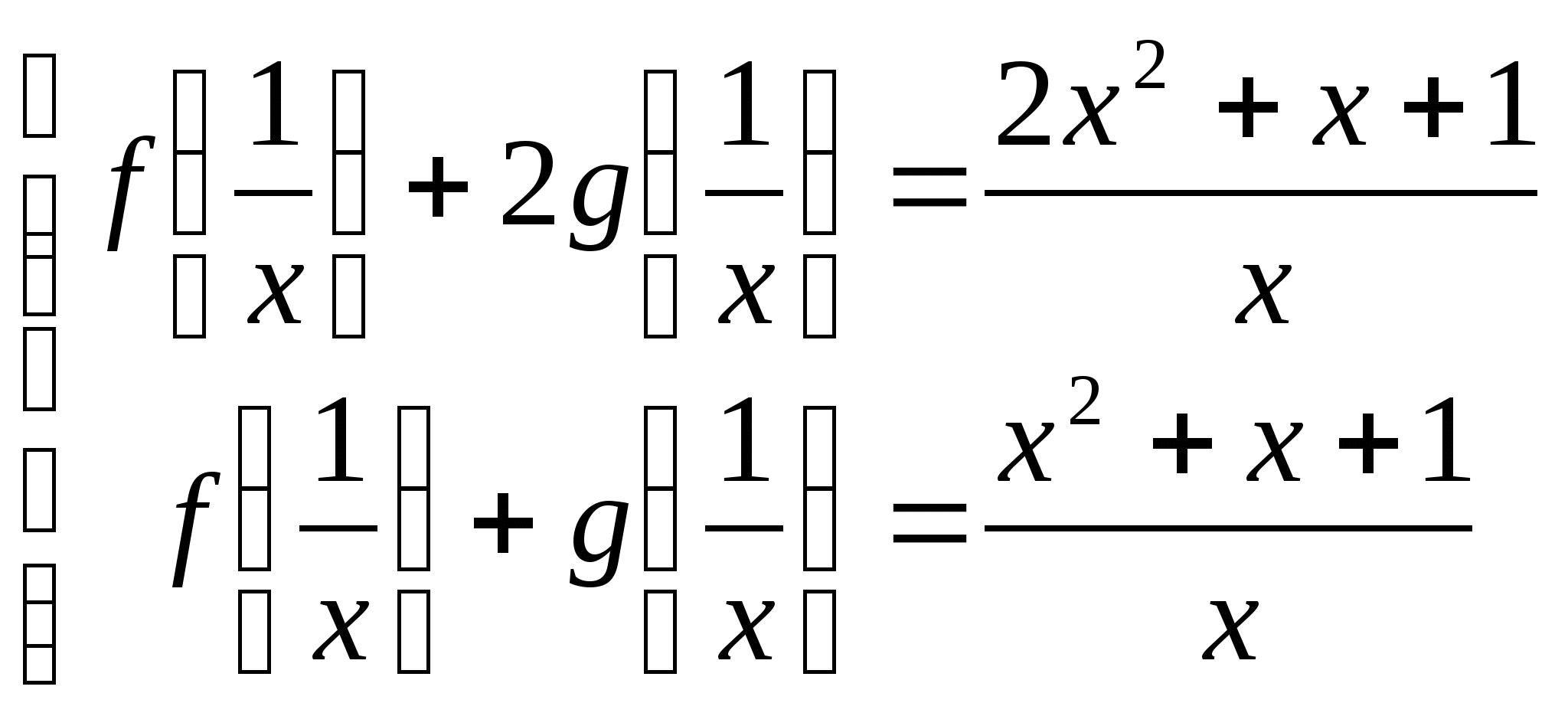 , решение которой
, решение которой ![]() ,
, ![]() .
.
1.3 Применение элементов математического анализа к решению функциональных уравнений
1.3.1 Предельный переход
Идею предельного перехода проиллюстрируем на следующих примерах.
Пример 14. Решить в классе непрерывных функций уравнение
![]() , где
, где ![]() . (10)
. (10)
Решение. Заменив ![]() на
на ![]() , получим
, получим
![]() .
(11)
.
(11)
Используя ту же замену, из уравнения (11) последовательно
получим ![]() ,
, ![]() ,...
,...
Методом математической индукции можно доказать, что 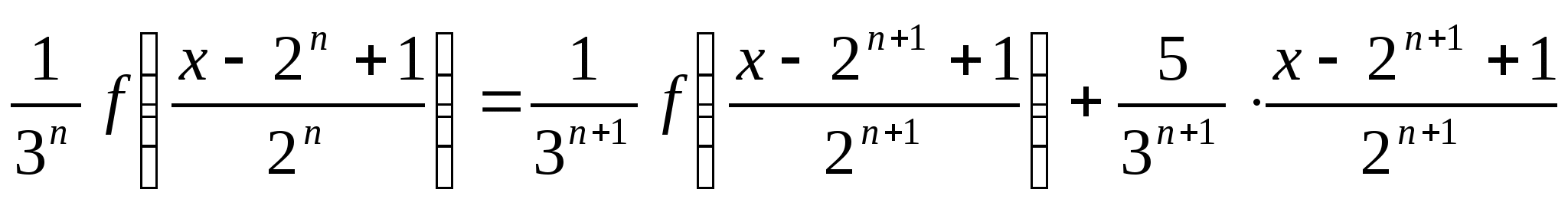 .
.
Сложив все уравнения, начиная с (11), получим 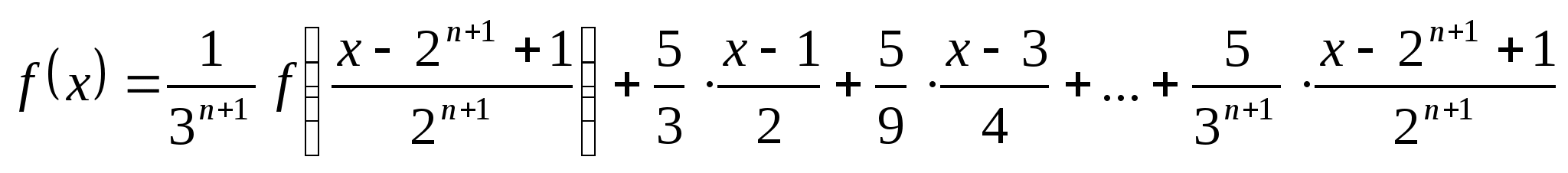 . (12)
. (12)
Так как функция ![]() непрерывна, то при любом фиксированном
непрерывна, то при любом фиксированном ![]()
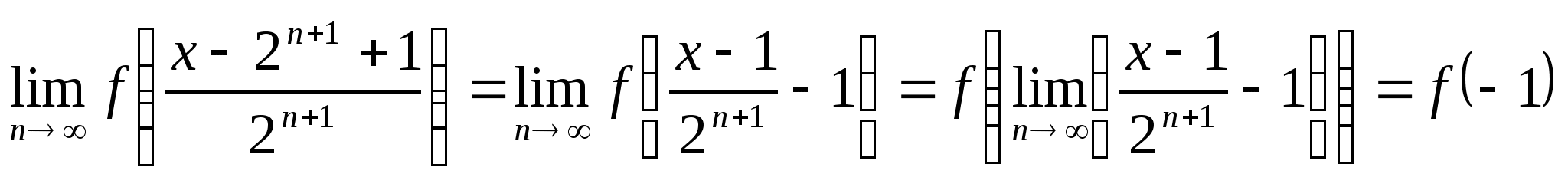 .
.
![]() Здесь
Здесь ![]() . Из уравнения (10)
. Из уравнения (10) ![]() . Тогда
. Тогда 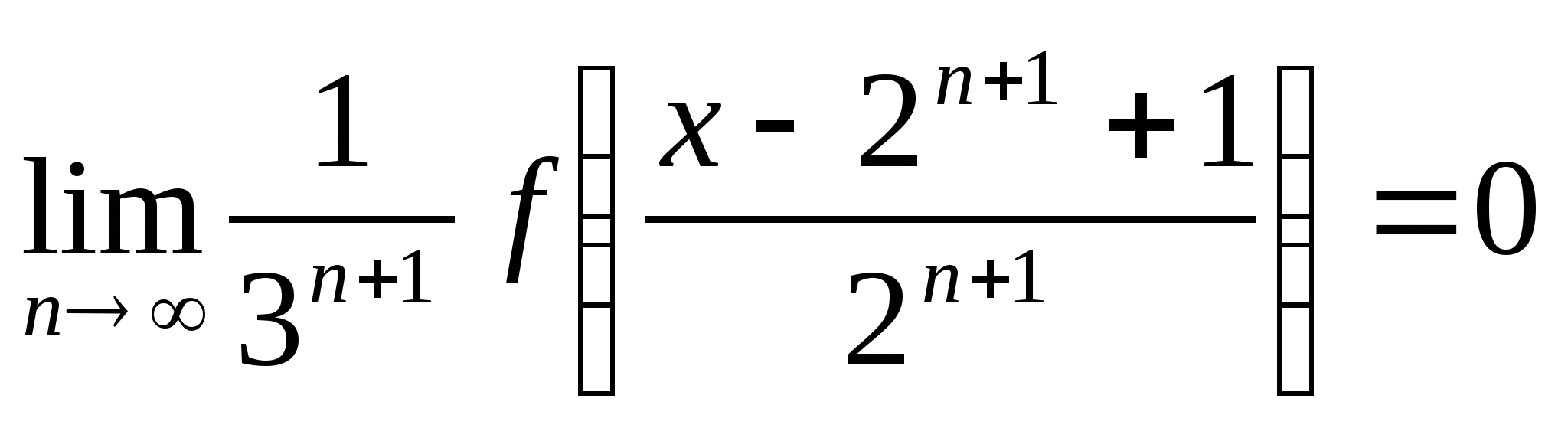 .
.
Левая часть равенства (12) не зависит от![]() ,
поэтому существует ее предел при
,
поэтому существует ее предел при![]() .
Переходя к пределу в равенстве, при
.
Переходя к пределу в равенстве, при ![]() имеем
имеем 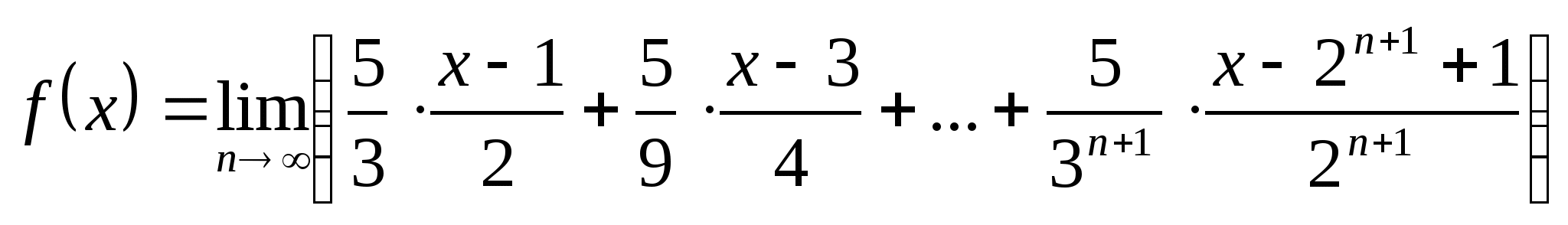 .
.
Правая часть является суммой трех бесконечно убывающих
прогрессий ![]() ,
, ![]() ,
, ![]() .
.
Итак,![]() ,
что и подтверждается проверкой.
,
что и подтверждается проверкой.
Пример 15. Доказать, что уравнение ![]() ,
, ![]() (13)
(13)
не имеет непрерывных решений.
Решение. Допустим, что существует непрерывное решение
функционального уравнения. Подставим в исходное уравнения вместо
![]() выражение
выражение ![]() , ведь если
, ведь если ![]() , то и
, то и![]() ,
получим:
,
получим: ![]() (14)
(14)
Теперь сделаем такую же замену ![]() в соотношении (13):
в соотношении (13): ![]() (15)
(15)
Описанную операцию проделаем ещё несколько pаз. На n-ом шаге
имеем: ![]()
Сложим все получившиеся выражения, начиная с (13) (всего будет
![]() выражений), и приведем подобные слагаемые:
выражений), и приведем подобные слагаемые: ![]() (16)
(16)
Равенство (16) верно для любого натурального ![]() . Зафиксируем
. Зафиксируем![]() ,
а
,
а ![]() устремим к ∞. Ввиду непрерывности
устремим к ∞. Ввиду непрерывности ![]() в точке
в точке![]() ,
находим
,
находим ![]() (17) , где
(17) , где ![]() .
.
В левой части (17) при конкретном (фиксированном) ![]() стоит некоторая константа, т.е. при данном
стоит некоторая константа, т.е. при данном ![]() ряд в правой части (17) сходится к этой константе. Мы же покажем,
что этот ряд расходится для любого значения
ряд в правой части (17) сходится к этой константе. Мы же покажем,
что этот ряд расходится для любого значения![]() ,
таким образом, придём к противоречию.
,
таким образом, придём к противоречию.
Для любого натурального ![]() и
и ![]() верно неравенство
верно неравенство ![]() , так что
, так что 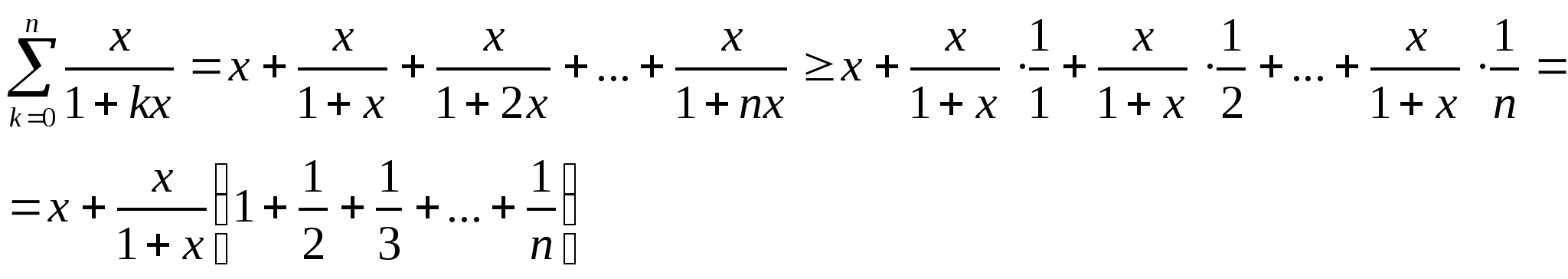
Гармонический ряд ![]() неограниченно возрастает при увеличении
неограниченно возрастает при увеличении ![]() (известный факт), следовательно,
(известный факт), следовательно, ![]() расходится к
расходится к![]() .
Что и требовалось доказать.
.
Что и требовалось доказать.
Пример 17. Найти![]() ,
ограниченную на любом конечном интервале, удовлетворяющую
функциональному уравнению:
,
ограниченную на любом конечном интервале, удовлетворяющую
функциональному уравнению: ![]() .
.
Решение. ![]() ;
;
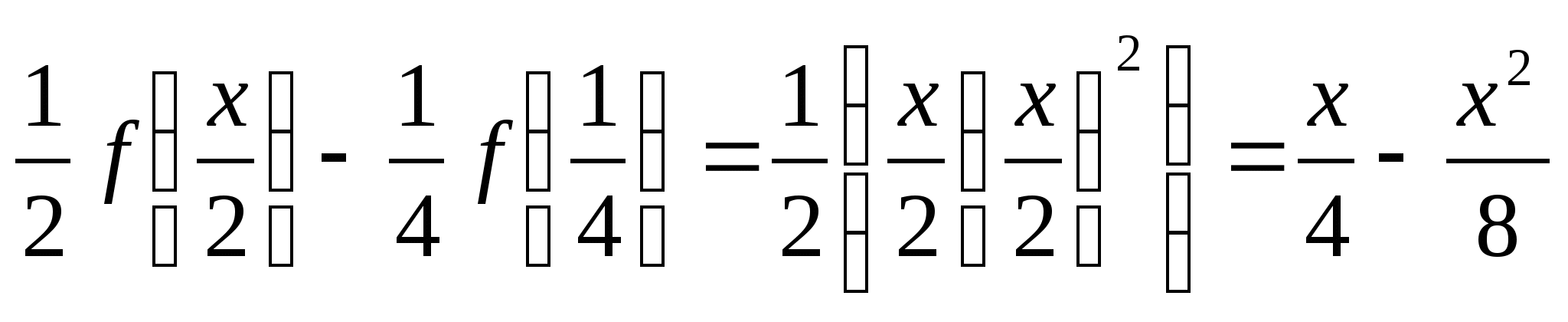 ,
,
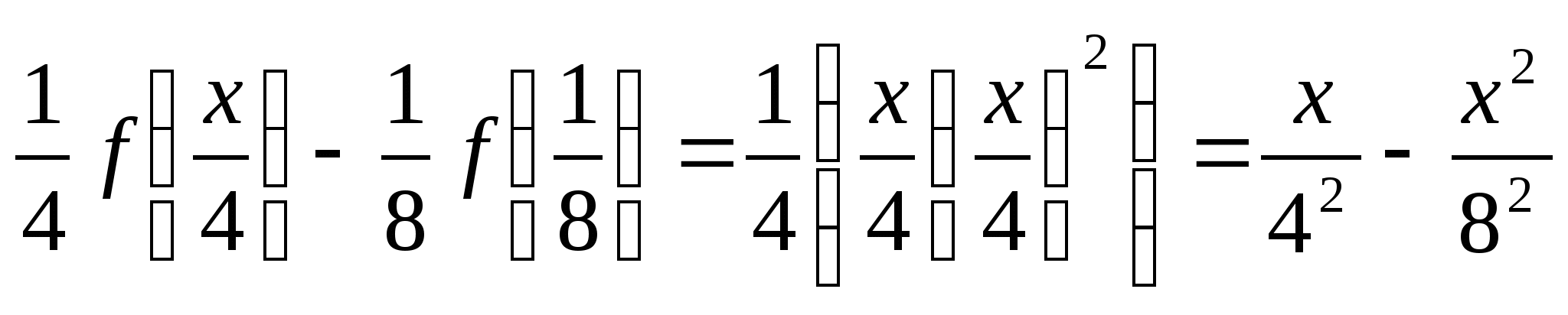 …
…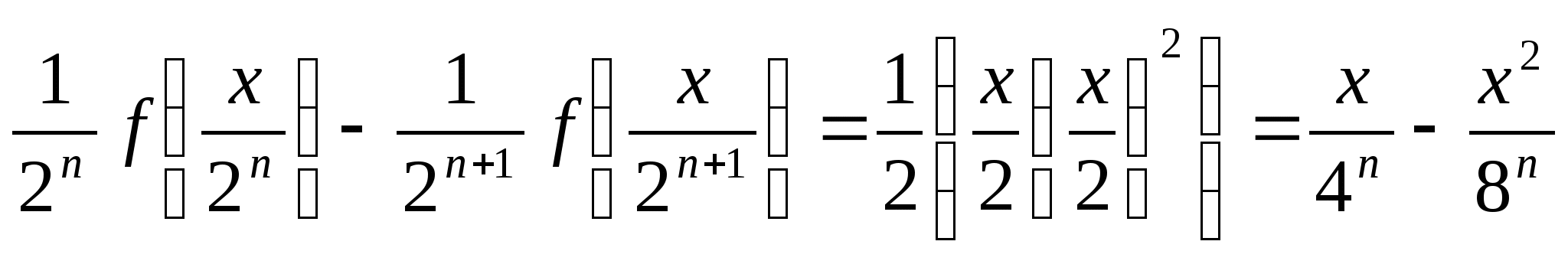 ,
,
![]()
переходя к ![]() при
при ![]() используя непрерывность
используя непрерывность ![]() и
и ![]() получаем, что
получаем, что ![]() .
.
Пример 18. Решить функциональное уравнение ![]() ,
, ![]() (18) в классе непрерывных функций.
(18) в классе непрерывных функций.
Решение. Выполнив замену![]() ,
получим
,
получим ![]() (19).
(19).
Складывая (18) с уравнением (19), умноженным на ![]() , получим
, получим ![]() .
.
Это уравнение решается аналогично уравнению (10). Найдем
подстановку, переводящую ![]() в
в ![]() . Для этого положим
. Для этого положим![]() .
Отсюда
.
Отсюда ![]() . Выполнив
. Выполнив ![]() раз подстановку
раз подстановку ![]() , получим систему уравнений, из которой находим
, получим систему уравнений, из которой находим
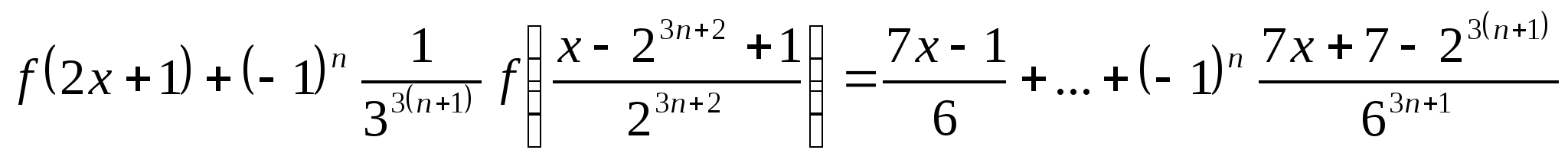
Отсюда при ![]()
![]() ,
или
,
или ![]() , что и подтверждается проверкой.
, что и подтверждается проверкой.
1.3.2 Дифференцирование
В некоторых случаях для нахождения решения функционального уравнения целесообразно продифференцировать обе части уравнения, если, конечно, производная существует. В результате получим функциональное уравнение, которое содержит и производную неизвестной функции. Решим это уравнение относительно производной. Тогда неизвестная функция является одной из первообразных для найденной производной. Этот метод уже применялся при решении уравнения Коши в классе дифференцируемых функций.
Пример 19. Найти в классе функций, имеющих непрерывные
производные, решение уравнения ![]() ,
, ![]() . (20)
. (20)
Решение. Попытки решить уравнение методом предельного перехода
не приводят к желаемому результату. Левая и правая части являются
функциями от![]() .
Они равны, следовательно, равны их производные по
.
Они равны, следовательно, равны их производные по ![]() . Продифференцируем и после сокращения получим
. Продифференцируем и после сокращения получим ![]() .
.
Это уравнение уже можно решить методом предельного перехода.
Выполнив подстановку ![]() , получим цепочку равенств
, получим цепочку равенств 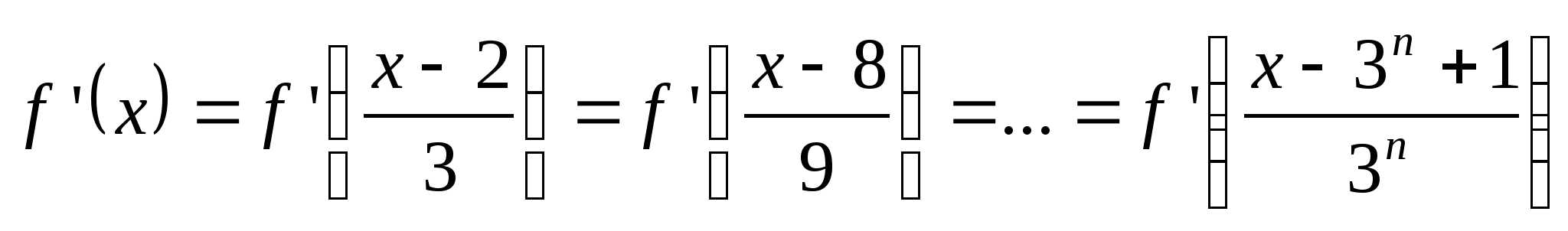 .
.
Ввиду непрерывности ![]() , при
, при![]() ,
имеем
,
имеем 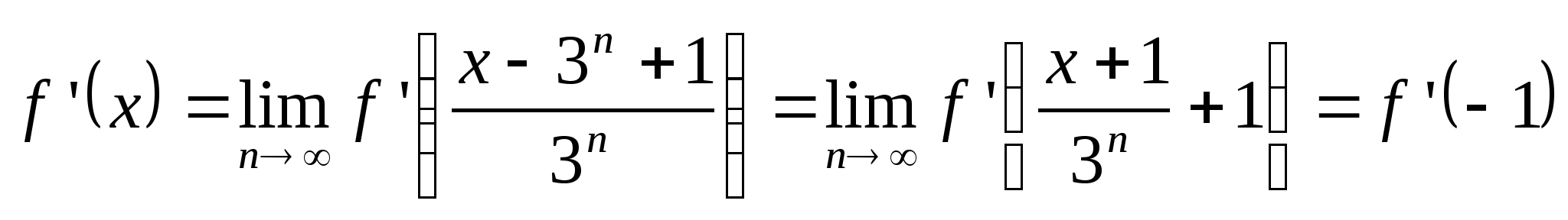
Итак,![]() ,
где
,
где ![]() . Первообразная функция
. Первообразная функция ![]() . Подставив в (20)
. Подставив в (20)![]() ,
получим
,
получим![]() .
Кроме того,
.
Кроме того, ![]() ,т.е.
,т.е. ![]() .
.
Легко проверить, что ![]() удовлетворяет условию при произвольном
удовлетворяет условию при произвольном ![]() .
.
Пример 20. Найти все действительные дифференцируемые функции,
удовлетворяющие функциональному уравнению ![]() (21) .
(21) .
Решение. Пусть ![]() удовлетворяет данному уравнению. Тогда
удовлетворяет данному уравнению. Тогда ![]() , т.е.
, т.е. ![]() , и, следовательно,
, и, следовательно,![]() .
.
После преобразований имеем ![]() , (22) откуда, с учётом
, (22) откуда, с учётом ![]() следует, что
следует, что ![]() (23) , где
(23) , где ![]() . Значит,
. Значит, 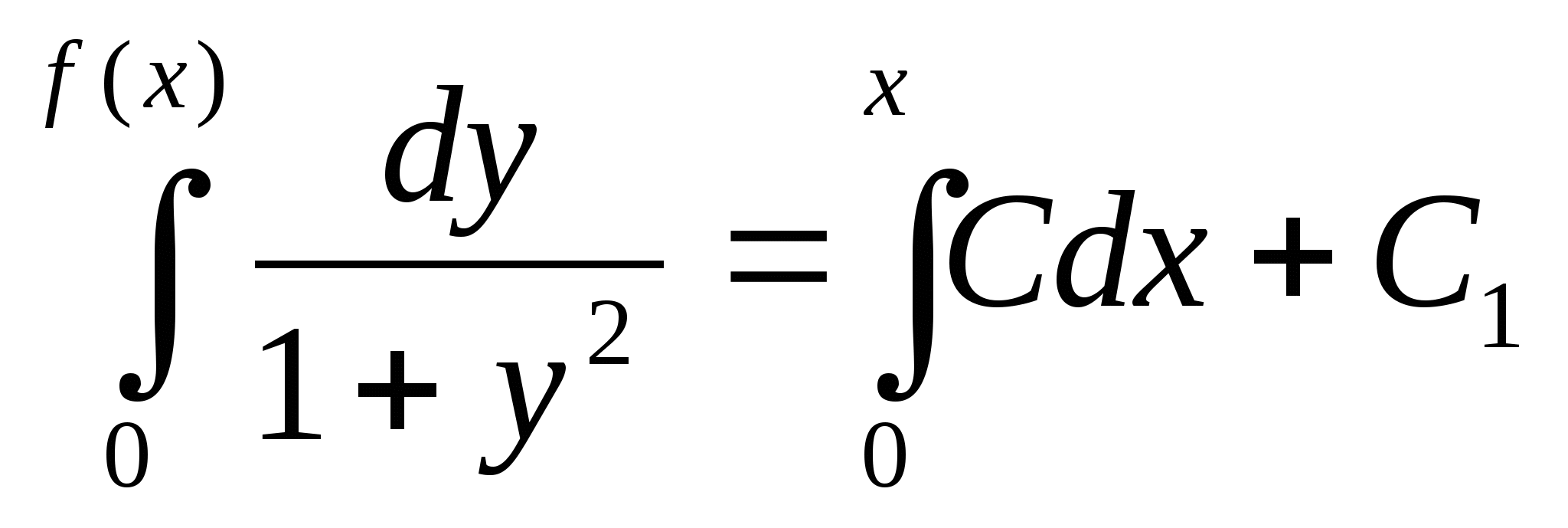 ,
, ![]() ,
, ![]() .
.
Условие ![]() означает, что
означает, что![]() ,
т.е.
,
т.е. ![]() . Очевидно, все функции вида
. Очевидно, все функции вида ![]() подходят под условие задачи.
подходят под условие задачи.
Пример 21. Найти функцию![]() ,
удовлетворяющую уравнению
,
удовлетворяющую уравнению ![]()
![]() ,
,![]() .
.
Решение. ![]() . Введём новые функции
. Введём новые функции ![]() ,
, ![]() .
.
Ясно, что функция ![]() - чётная, а
- чётная, а ![]() - нечётная функции, причём
- нечётная функции, причём![]() .
Получим уравнение относительно новых функций
.
Получим уравнение относительно новых функций ![]() и
и ![]() :
:![]() ,
,
![]() ,
, ![]() ,
, ![]() . Так как
. Так как ![]() , то
, то ![]() и
и ![]()
Непосредственной проверкой убеждаемся в том, что при любых
числах![]() ,
а функция
,
а функция ![]() является решением исходного уравнения.
является решением исходного уравнения.
Таким образом, поиск решения функционального уравнения сильно зависит от класса функций, в котором ищется решение. Мы рассмотрели некоторые методы решения функциональных уравнений. Особое место в теории функциональных уравнений занимают разностные уравнения, которые используются при решении многих прикладных задач.
2. Определение основных элементарных функций с помощью функциональных уравнений
При решении различных математических задач чаще других используются некоторые функции. Очевидно, что эти функции, наиболее, изучены и названы элементарными. Среди элементарных функций выделяют основные элементарные функции.
Функции ![]() , где
, где ![]() - const,
- const, ![]() (степенная),
(степенная), ![]() (
(![]() ,
показательная),
,
показательная), ![]() (
(![]() ,
логарифмическая),
,
логарифмическая), ![]() (тригонометрические),
(тригонометрические), ![]() (обратные тригонометрические), называются основными элементарными
функциями.
(обратные тригонометрические), называются основными элементарными
функциями.
Всякая функция, которая может быть явным образом задана с помощью формулы, содержащей конечное число арифметических операций, называется элементарной.
Например: ![]() ,
, ![]() элементарные функции.
элементарные функции.
Рассмотрев элементарные функции, определим их, как решение функционального уравнения. Эта глава будет посвящена определению основных элементарных функций с помощью функциональных уравнений.
2.1 Линейная функция.
Для определения линейной функции составим функциональное
уравнение, единственным решением которого является линейная
функция. ![]() .
.
Найдем разность и сумму двух различных значений линейной
функции: ![]() и
и ![]() .
.
![]() (24)
(24)
![]() (25)
(25)
Запишем уравнение (24) в виде функционального ![]() (26)
(26)
Проверим второе функциональное уравнение на основании равенства (25).
![]() (27)
(27)
Докажем, что из уравнения (26) можно получить уравнение (27).
Убедимся в том, что любое решение уравнения (26) является нечетной
функцией. Для этого в уравнение (26) вместо ![]() подставим
подставим ![]() . Воспользуемся тем, что из вида линейной функции следует:
. Воспользуемся тем, что из вида линейной функции следует:![]() .
Таким образом, докажем, что
.
Таким образом, докажем, что ![]() . Затем вновь заменим x2 на x1 в уравнении
(26), получим уравнение (27). Итак, каждое решение уравнения (26)
является решением уравнения (27).
. Затем вновь заменим x2 на x1 в уравнении
(26), получим уравнение (27). Итак, каждое решение уравнения (26)
является решением уравнения (27).
Докажем, что уравнение (27) можно преобразовать к виду уравнения (26).
Из проведенных выше рассуждений следует, что множество решений уравнений (26) и (27) совпадает, следовательно, эти уравнения эквивалентны.
Определение 1. Множество всех функциональных уравнений, имеющих
одно и то же множество решений на множестве ![]() , будем называть классом функциональных уравнений на этом
множестве.
, будем называть классом функциональных уравнений на этом
множестве.
Так как все уравнения из класса уравнений, определяющих линейную функцию эквивалентны, то класс уравнений можно обозначить любым уравнением, например, уравнением (26).
Определение 2. Решением класса функциональных уравнений на
множестве ![]() будем называть функцию, являющуюся решением каждого уравнения
класса на множестве
будем называть функцию, являющуюся решением каждого уравнения
класса на множестве ![]() .
.
Докажем, что линейную функцию можно определить как решение класса функциональных уравнений (26).Для того чтобы выделить линейную функцию, как единственное решение будем искать решение с заранее заданными свойствами:
-
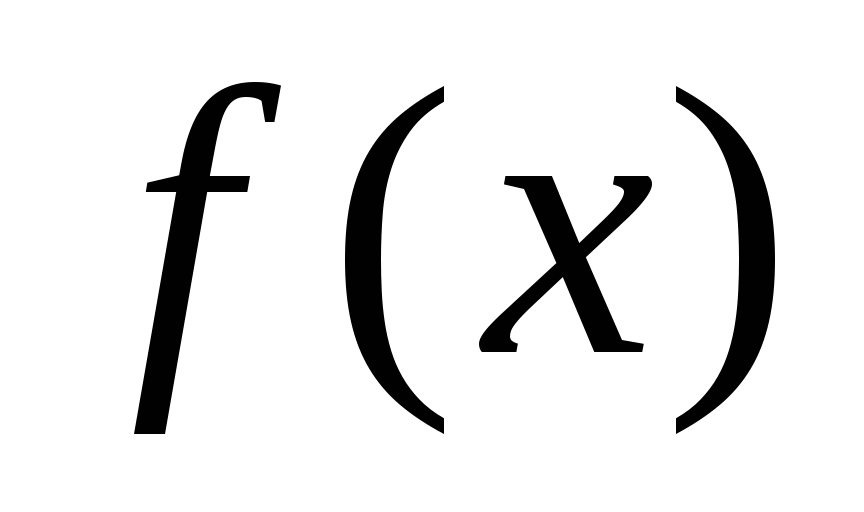 непрерывная
функция в интервале
непрерывная
функция в интервале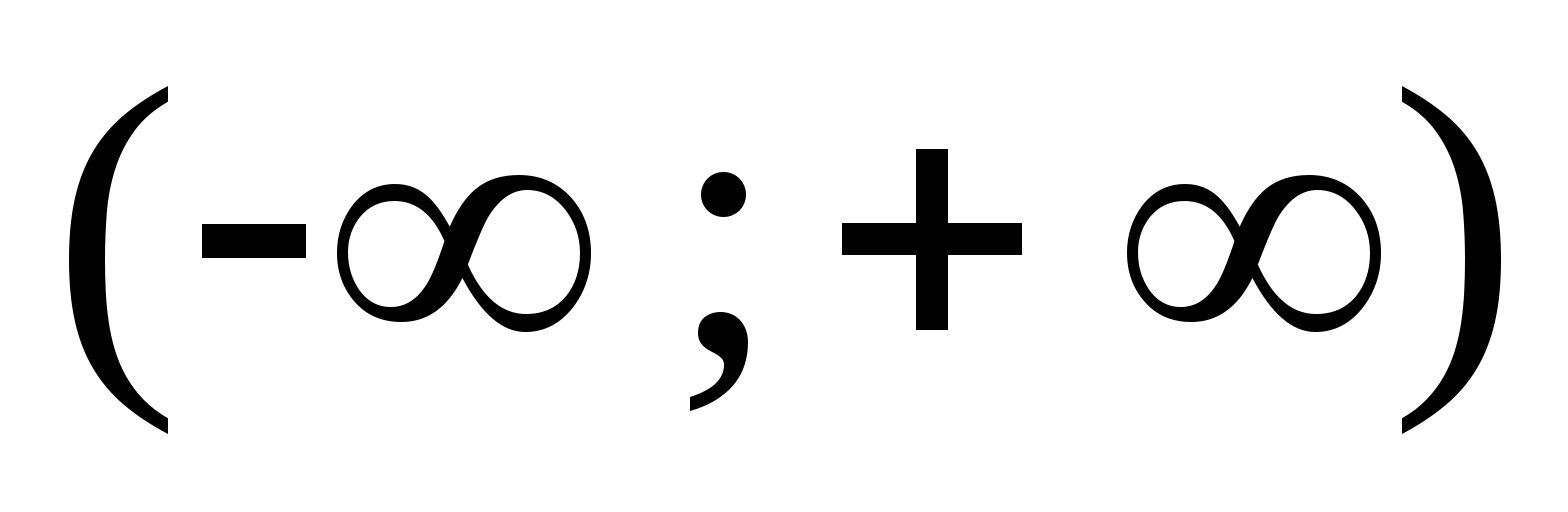 ;
;
-
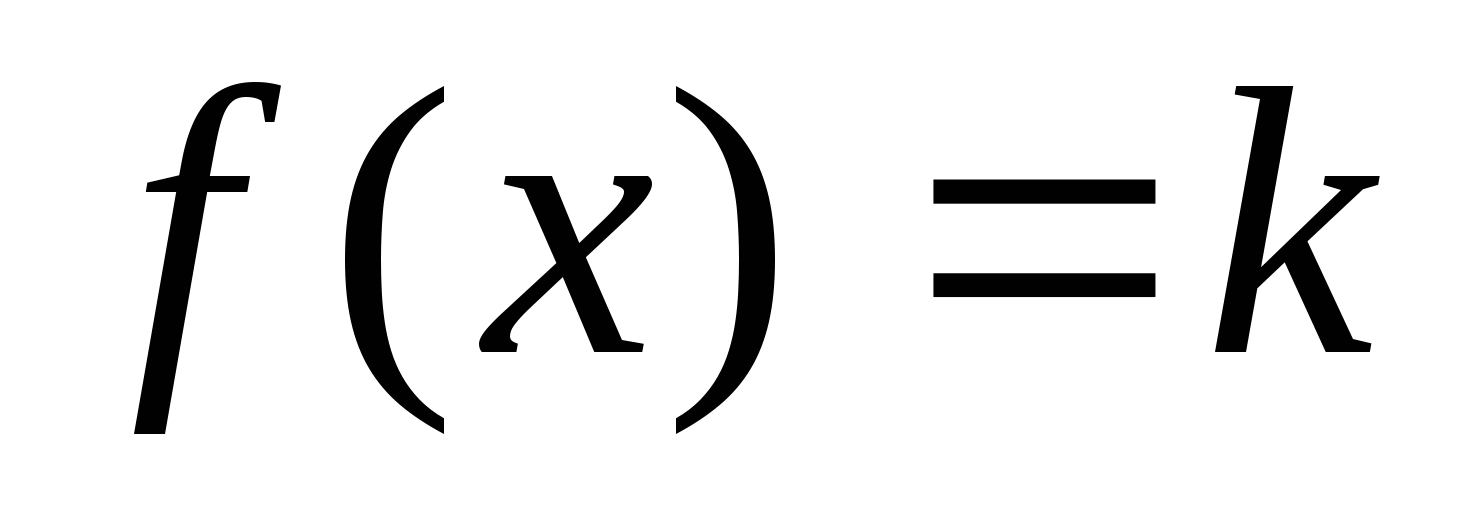 ,
,
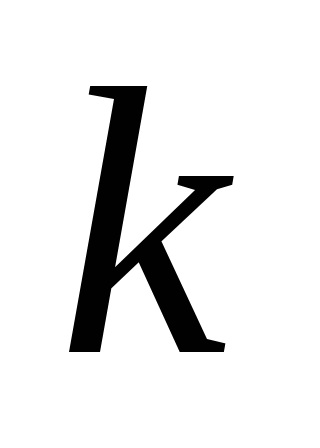 - произвольное действительное число.
- произвольное действительное число.
Предварительно докажем, что любое решение ![]() функционального уравнения (26) таково, что:
функционального уравнения (26) таково, что:
а) ![]() . Полагая в уравнении (26)
. Полагая в уравнении (26) ![]() , получаем
, получаем ![]() . Это равенство справедливо только в одном случае, когда
. Это равенство справедливо только в одном случае, когда ![]() ;
;
б) ![]() . Так как
. Так как ![]() , то
, то ![]() . В силу произвольности х функция
. В силу произвольности х функция ![]() нечетна.
нечетна.
Теорема 1. Решение класса функциональных уравнений (26) при условиях 1), 2) является линейной функцией.
Доказательство. Методом Коши докажем, что при любом
действительном ![]()
![]() . Сначала докажем это равенство для
. Сначала докажем это равенство для![]() .
Полагая в уравнении (24) последовательно y равным
.
Полагая в уравнении (24) последовательно y равным![]() ,
…, будем получать:
,
…, будем получать:
![]() ,
,
![]() ,
,
![]() ,
,
……………………….
Закономерности, которые видны в этих равенствах, позволяют выдвинуть гипотезу вида
![]() (28)
(28)
Это вспомогательное равенство. Докажем его методом
математической индукции. При ![]() равенство (28) очевидно. Предположим, что равенство (28)
справедливо для некоторого натурального
равенство (28) очевидно. Предположим, что равенство (28)
справедливо для некоторого натурального ![]() и докажем его справедливость для следующего натурального числа
и докажем его справедливость для следующего натурального числа
![]() .
.
Так как ![]() , то утверждение доказано.
, то утверждение доказано.
Полагая в равенстве (28)![]() ,
получим
,
получим ![]() или
или
![]() ,
(29)
,
(29)
где ![]() . Следовательно, равенство
. Следовательно, равенство ![]() справедливо для
справедливо для ![]() .
.
Пусть теперь ![]() - любое положительное рациональное число.
- любое положительное рациональное число.
Тогда, полагая в равенстве (28) ![]() , получим
, получим ![]() или
или ![]() ; учитывая равенство (29), находим
; учитывая равенство (29), находим ![]() . Значит, равенство
. Значит, равенство ![]() справедливо для
справедливо для ![]() .
.
В силу свойства б) ![]() , следовательно,
, следовательно, ![]() . Значит, равенство
. Значит, равенство ![]() справедливо и для
справедливо и для![]() ,
а поэтому справедливо и для всех
,
а поэтому справедливо и для всех ![]() . Пусть теперь
. Пусть теперь![]() -любое
действительное число. Тогда найдется последовательность
рациональных чисел
-любое
действительное число. Тогда найдется последовательность
рациональных чисел ![]() такая, что
такая, что ![]() при
при![]() .
Так как, по доказанному,
.
Так как, по доказанному, ![]() , то, переходя в этом равенстве к пределу при
, то, переходя в этом равенстве к пределу при ![]() ( что возможно в силу непрерывности функции
( что возможно в силу непрерывности функции![]() ),
получим
),
получим ![]() или
или ![]() .
.
Из проведенных рассуждений следует однозначность решения функционального уравнения, так как это решение можно представить в заданном виде.
Определение 3.Класс уравнения (26) назовем классом уравнений, определяющих линейную функцию при выполнении условий 1) и 2).
Исследуем дальнейшие свойства линейной функции.
Исследуем монотонность линейной функции. Положим в уравнении
(27) ![]() ,
, ![]() ,
, ![]() . Тогда получим
. Тогда получим ![]() или
или ![]() (30)
(30)
Если ![]() , то правая часть равенства (30) больше нуля
, то правая часть равенства (30) больше нуля ![]() и, значит,
и, значит, ![]() , то есть функция
, то есть функция ![]() строго возрастает.
строго возрастает.
Если ![]() , то правая часть равенства (30) меньше нуля
, то правая часть равенства (30) меньше нуля ![]() и, значит,
и, значит, ![]() , то есть функция
, то есть функция ![]() строго убывает.
строго убывает.
Исследуем ограниченность линейной функции. Найдем пределы
линейной функции при стремящемся к бесконечности аргументе, так как
при каждом конечном значении аргумента линейная функция также
принимает конечное значение. Переход в равенстве (28) к пределу
при![]() ,
имеем
,
имеем ![]() .
.
Аналогично: ![]()
При требовании непрерывности класс уравнений (26) имеет своим
решением определенный вид элементарных функций ![]() .
.
Определение 4. Решение класса функциональных уравнений (26) при
условиях 1) и 2) называется линейной функцией и обозначается
![]() .
.
2.2 Показательная функция
Составим функциональное уравнение, решение которого однозначно
определит показательную функцию. Используем для этого
равенства:![]()
(31)
![]()
(32)
![]()
(33)
![]()
(34)
Запишем четыре функциональных уравнения, соответствующих уравнениям (31) - (34) и пронумеруем их соответственно (35) - (38).
(35)
![]()
(36)
![]()
(37)
![]()
(38)
Так как уравнения (35) - (38) эквиваленты, то далее будем исследовать класс уравнений (35). Рассмотрим решение этого уравнения, удовлетворяющее условиям:
-
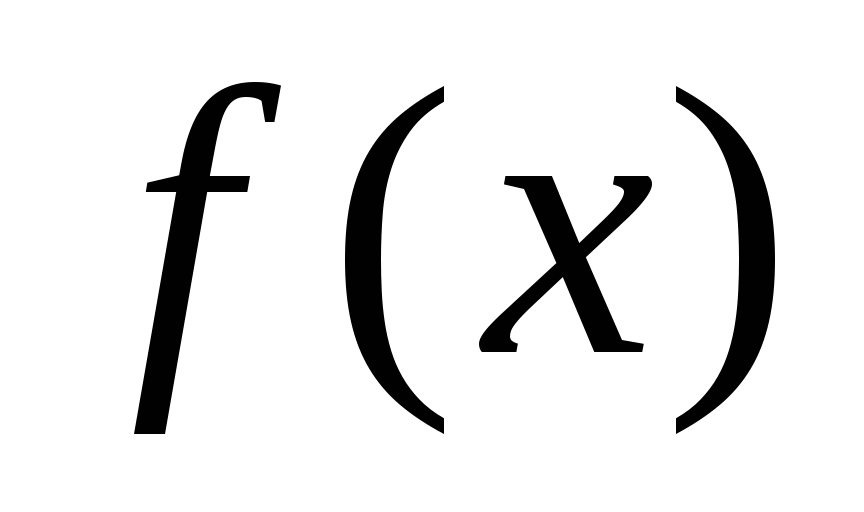 непрерывная
функция в интервале
непрерывная
функция в интервале 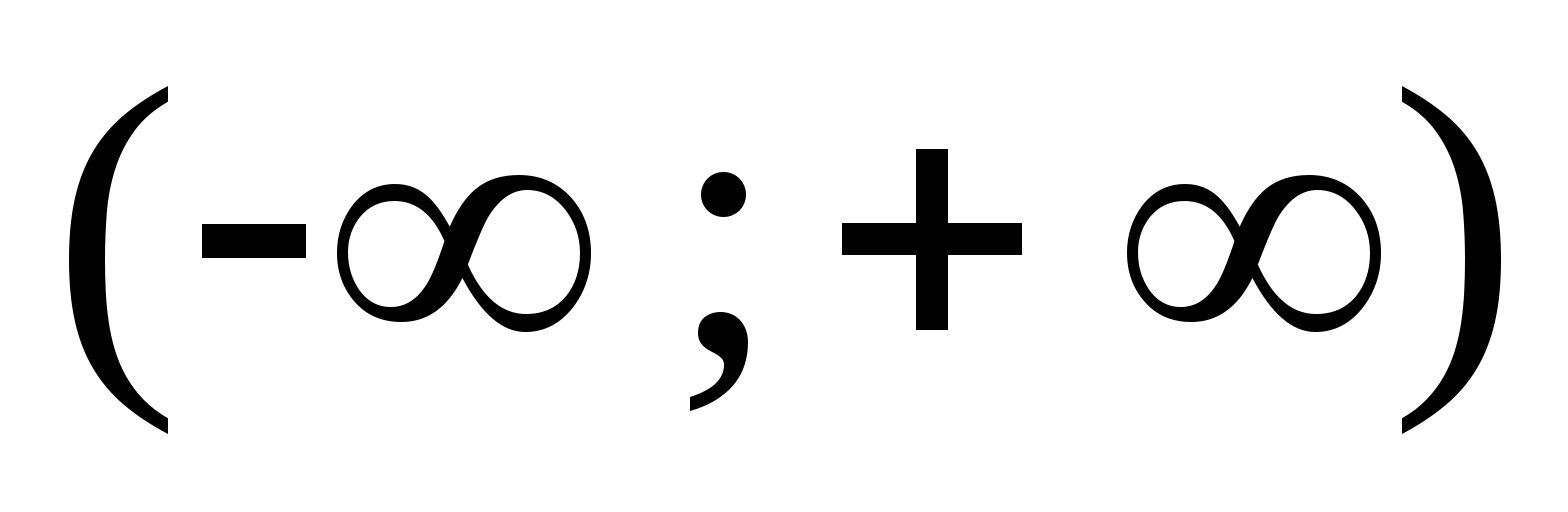 ;
;
-
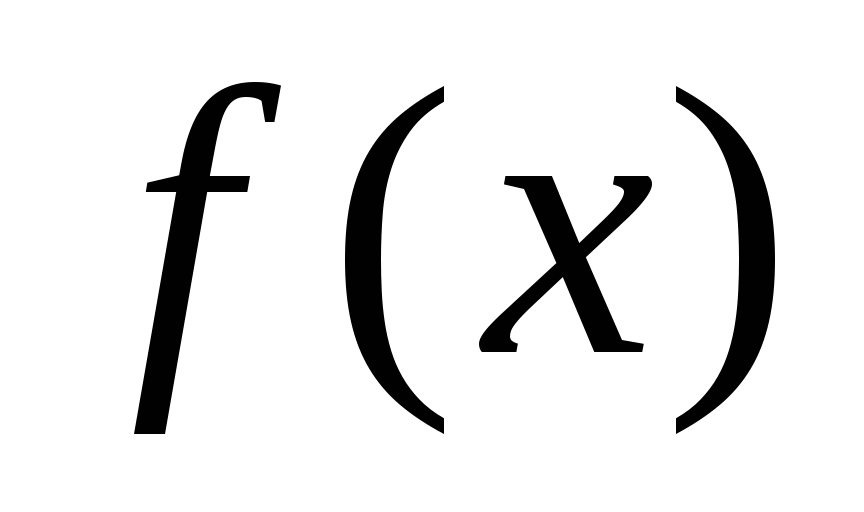 не
тождественно равна нулю;
не
тождественно равна нулю;
-
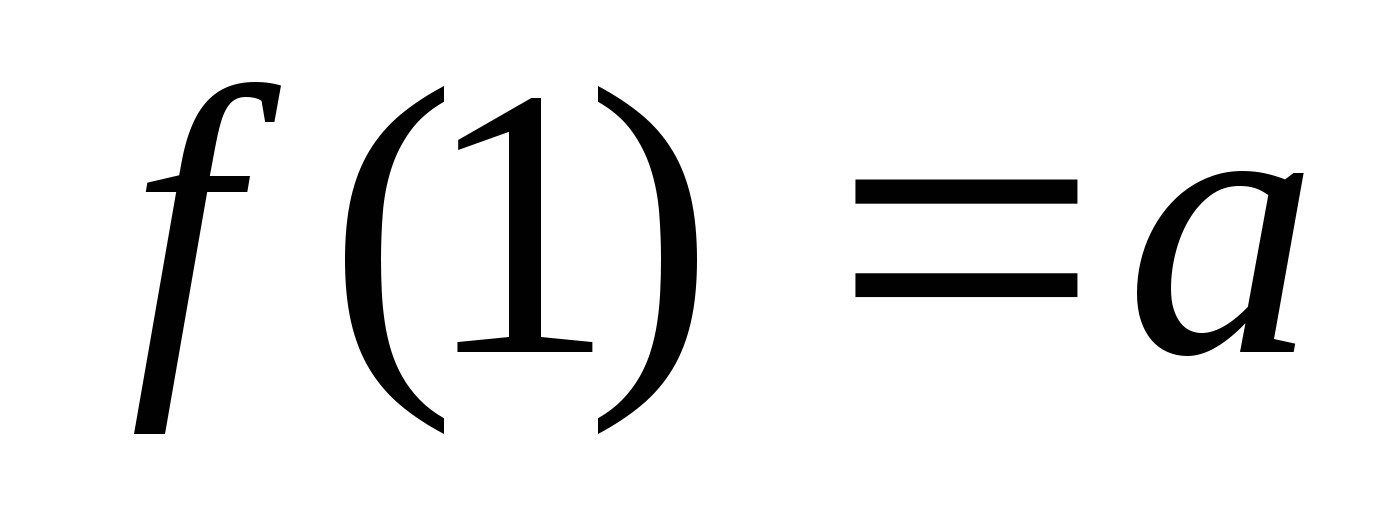
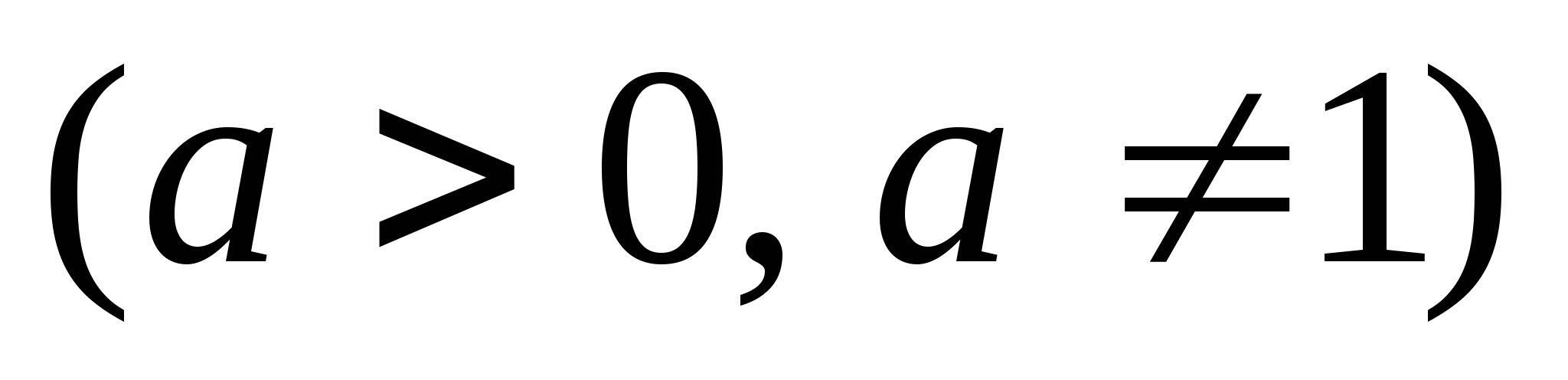 .
.
Теорема 2. Решение класса функциональных уравнений (35) при
условиях 1) - 3) имеет вид![]() .
.
Доказательство. По условию теоремы функция ![]() не тождественно равна нулю, следовательно, существует такое
значение
не тождественно равна нулю, следовательно, существует такое
значение![]() ,
что
,
что![]() .
Обозначим
.
Обозначим![]() .
Подставим указанное
.
Подставим указанное ![]() в уравнение (35). Получим
в уравнение (35). Получим ![]() , в силу произвольности
, в силу произвольности ![]() функция
функция ![]() отлична от нуля при любом
отлична от нуля при любом ![]() . Более того, можно уточнить еще
. Более того, можно уточнить еще![]() ,
так как
,
так как 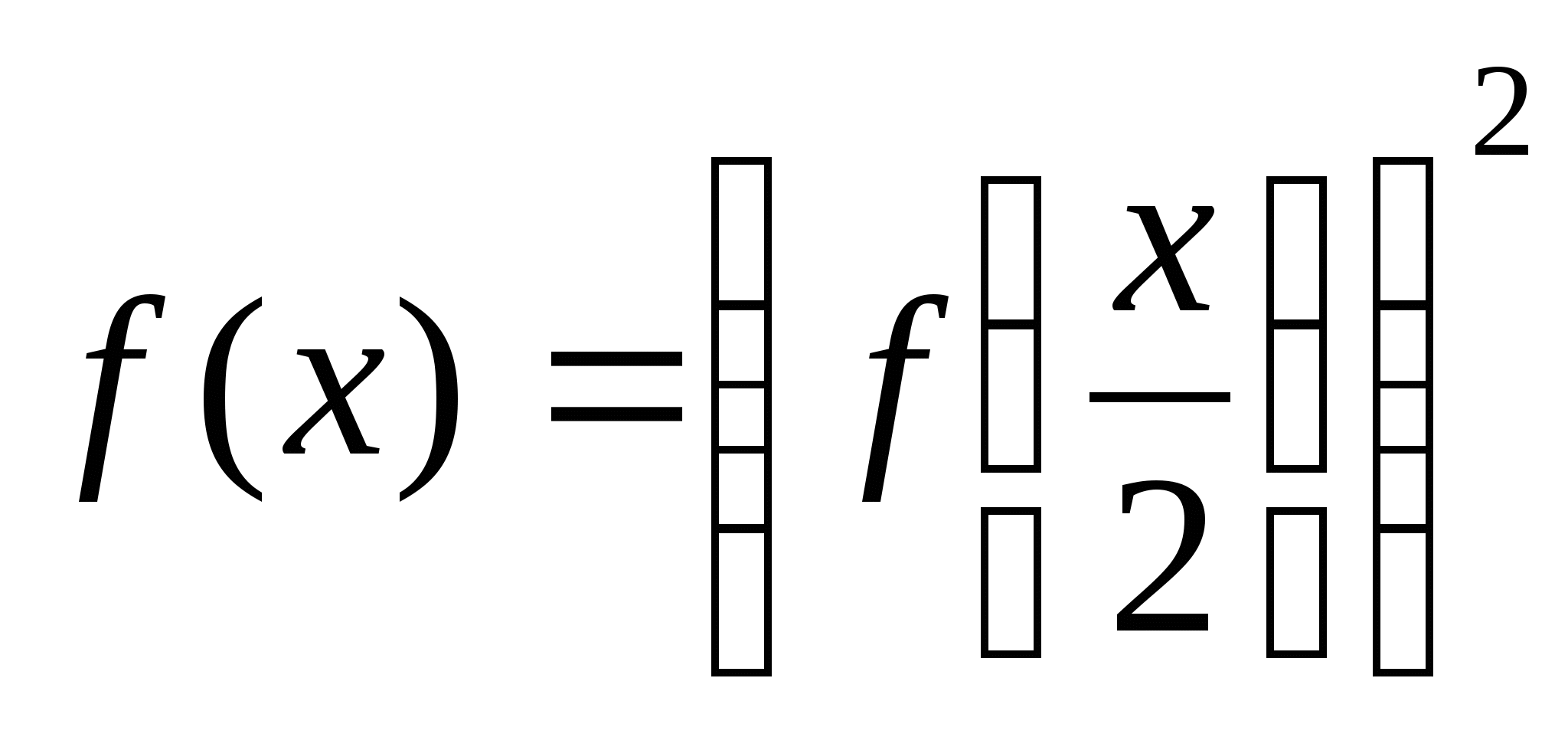 . Далее используем определение логарифма из средней школы.
Прологарифмируем уравнение (35)
. Далее используем определение логарифма из средней школы.
Прологарифмируем уравнение (35) ![]() . Введем новую функцию
. Введем новую функцию![]() .
Функция
.
Функция ![]() непрерывна как композиция непрерывных функций и по определению
удовлетворяет уравнению
непрерывна как композиция непрерывных функций и по определению
удовлетворяет уравнению ![]() .
.
Получено уравнение, решение которого, удовлетворяющим условиям
1) - 3), является только линейная функция, поэтому ![]() ,
, ![]() - произвольная константа. По определению логарифма
- произвольная константа. По определению логарифма ![]() . Так как
. Так как ![]() , то можно обозначить
, то можно обозначить ![]() . Теорема доказана.
. Теорема доказана.
Методом математической индукции докажем, что для любого
![]() справедливо равенство
справедливо равенство
![]() .
(39)
.
(39)
Действительно, при ![]() это равенство очевидно. Предположим, что оно верно для некоторого
натурального
это равенство очевидно. Предположим, что оно верно для некоторого
натурального ![]() и докажем его справедливость для следующего натурального
числа
и докажем его справедливость для следующего натурального
числа![]() .
Рассмотрим
.
Рассмотрим ![]() . Из уравнения (35) имеем
. Из уравнения (35) имеем ![]() , что и требовалось показать.
, что и требовалось показать.
При ![]() равенство (39) дает значение функции
равенство (39) дает значение функции ![]() при натуральных значениях аргумента:
при натуральных значениях аргумента: ![]() или
или ![]() . Полагая в равенстве (35)
. Полагая в равенстве (35) ![]() , получим
, получим ![]() или
или ![]() , то есть мы получили значения функции
, то есть мы получили значения функции ![]() при положительных значениях аргумента
при положительных значениях аргумента ![]() . Так как
. Так как ![]() , то
, то 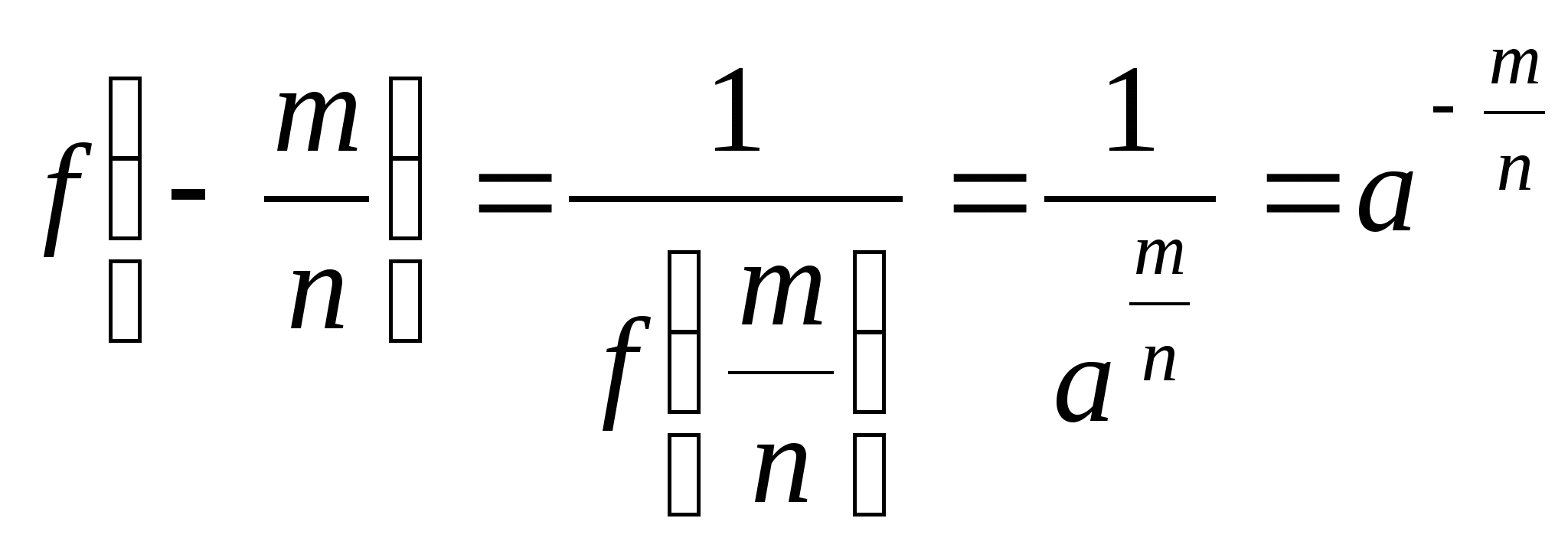 .
.
Таким образом, для любого рационального значения аргумента
![]() имеем
имеем![]() .
Пусть теперь
.
Пусть теперь ![]() - любое действительное число, а
- любое действительное число, а![]() -
последовательность рациональных чисел, сходящихся к
-
последовательность рациональных чисел, сходящихся к ![]() . Но по доказанному
. Но по доказанному ![]() . Переходя в этом неравенстве к пределу при
. Переходя в этом неравенстве к пределу при ![]() и учитывая, что функция
и учитывая, что функция ![]() непрерывна, получим
непрерывна, получим ![]() .
.
Теорема доказана.
Определение 5. Класс уравнений (35) назовем классом уравнений, определяющих показательную функцию при условиях 1) - 3).
Исследуем свойства показательной функции, заданной как решение
класса функциональных уравнений (35). Установим вначале несколько
свойств решений этого класса. Пусть ![]() - произвольное решение класса.
- произвольное решение класса.
а) ![]() . По условию теоремы существует такое
. По условию теоремы существует такое![]() ,
что
,
что ![]() . Тогда для любого
. Тогда для любого ![]() имеем на основании уравнения (35)
имеем на основании уравнения (35) ![]() .
.
Отсюда ![]() и, значит,
и, значит, ![]() .
.
Сформулируем доказанное свойство, используя понятие множества значений функции.
б) ![]()
![]() .
Так как
.
Так как ![]() и
и ![]() , то
, то ![]() .
.
в) ![]() .
.
Полагая в уравнении (35)![]() ,
получим
,
получим ![]() или
или ![]() . Следовательно,
. Следовательно, ![]()
г) Исследуем показательную функцию на монотонность. Полагая в
уравнении (35) ![]() ,
, ![]() , получим
, получим ![]() . Преобразуем разность
. Преобразуем разность
![]() (40)
(40)
Пусть![]() ,
,
![]() . При этом правая часть равенства (40) положительна и,
следовательно,
. При этом правая часть равенства (40) положительна и,
следовательно, ![]() . Значит функция
. Значит функция ![]() строго возрастает на интервале
строго возрастает на интервале ![]() . Аналогично доказывается строгое убывание функции
. Аналогично доказывается строгое убывание функции ![]() строго убывает на интервале
строго убывает на интервале ![]() при
при ![]() .
.
е) Исследуем показательную функцию на ограниченность. Найдем
предельные значения функции ![]() при
при ![]() . Учитывая непрерывность функции
. Учитывая непрерывность функции ![]() и ее строгое возрастание (убывание) на интервале
и ее строгое возрастание (убывание) на интервале ![]() , будем рассматривать пределы функции по множеству целых чисел.
, будем рассматривать пределы функции по множеству целых чисел.
Так как ![]() , то при
, то при ![]()
![]() , а при
, а при ![]()
![]() . Следовательно, при
. Следовательно, при ![]()
![]() ,
при
,
при ![]()
![]() .
Аналогично доказывается, что при
.
Аналогично доказывается, что при ![]()
![]() ,
при
,
при ![]()
![]() .
.
Определение 6. Решение класса функциональных уравнений (35) при
условиях 1) - 3) называется показательной функцией и обозначается
![]() .
.
2.3 Определение логарифмической функции
Для составления класса уравнений, определяющих логарифмическую функцию , используем свойства логарифмов:
(41)
![]()
(42)
Составим соответствующие функциональные уравнения
(43)
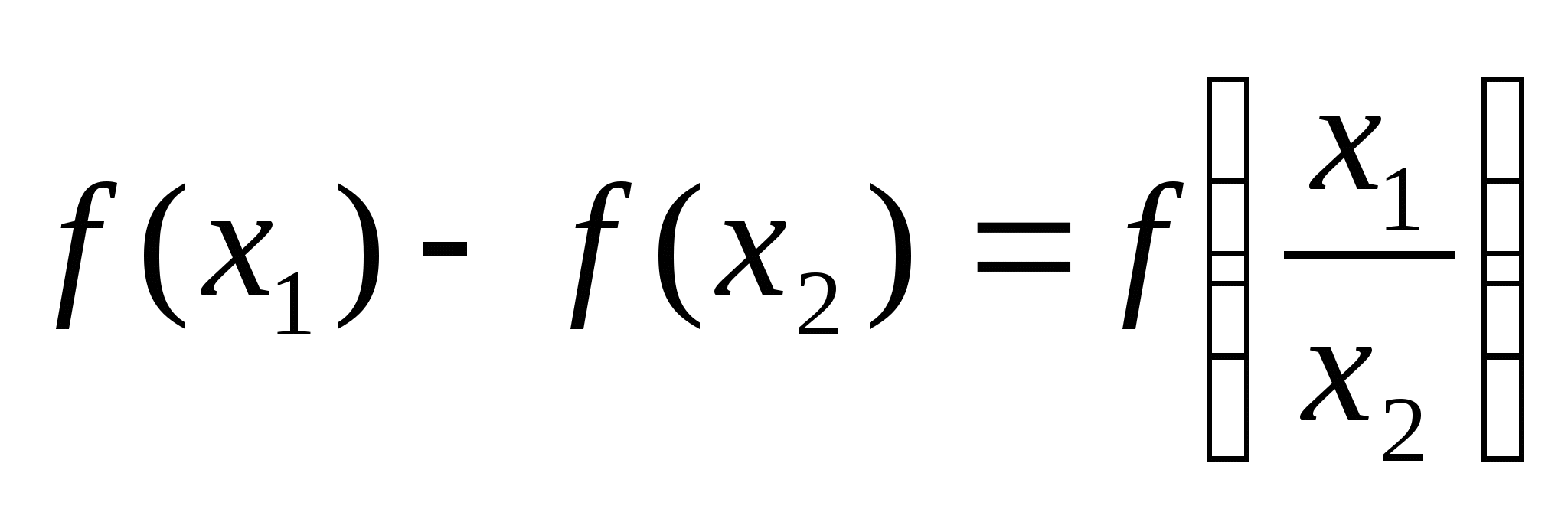
(44)
Докажем эквивалентность полученных уравнений (43),(44).
Рассмотрим уравнение (43) при следующих условиях:
-
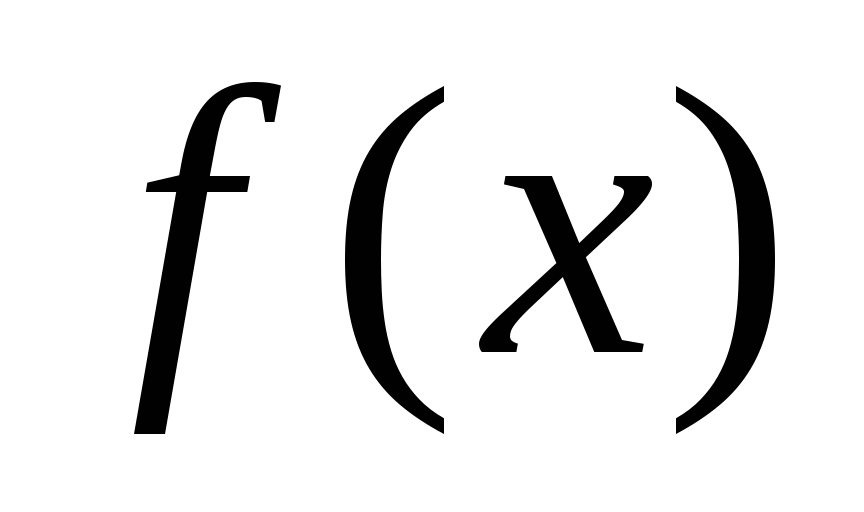 непрерывна
и отлична от постоянной функции в интервале
непрерывна
и отлична от постоянной функции в интервале 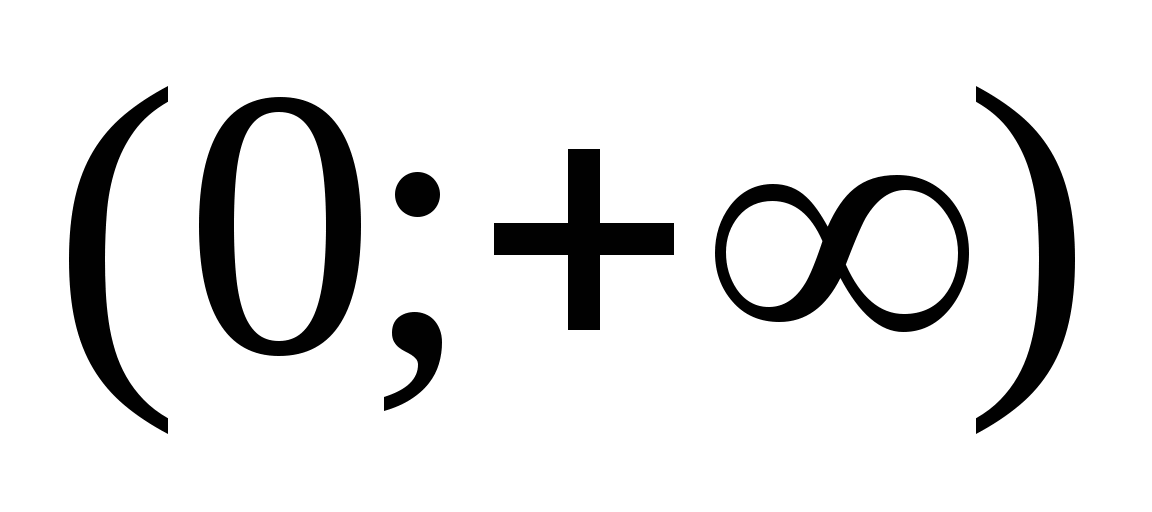 ;
;
-
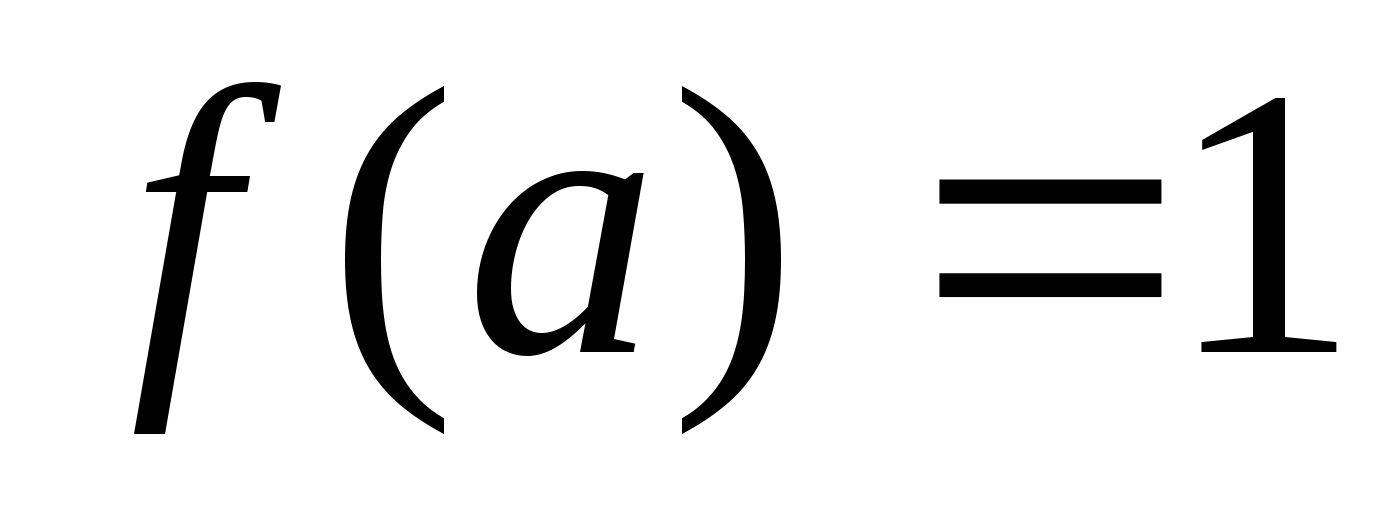
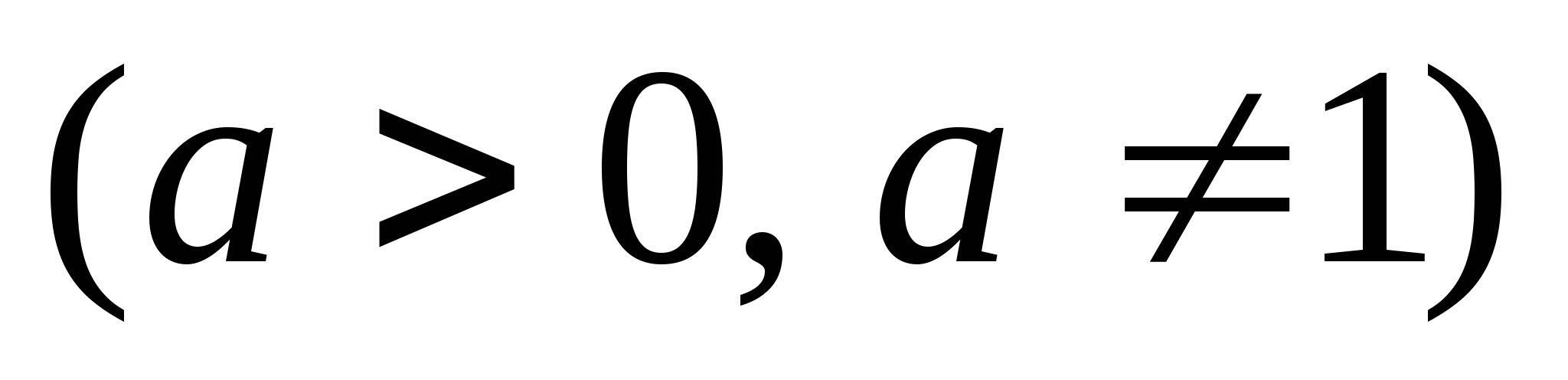 .
.
Теорема 3. Класс функциональных уравнений (43) при условиях 1), 2) имеет единственное решение.
Доказательство. Для доказательства единственности решения
функционального уравнения рассмотрим произвольное решение ![]() и введем замену переменных. Заменяя
и введем замену переменных. Заменяя ![]() на
на ![]() по формуле
по формуле![]() ,
получим
,
получим ![]() . Аналогично
. Аналогично ![]() , то есть
, то есть![]() .
При этом
.
При этом ![]() . C новой функцией уравнение (43) примет вид
. C новой функцией уравнение (43) примет вид ![]() функционального уравнения, определяющего линейную функцию при
известных условиях. При этом функция
функционального уравнения, определяющего линейную функцию при
известных условиях. При этом функция ![]() непрерывна как композиция двух непрерывных функций и
непрерывна как композиция двух непрерывных функций и
![]() .
Таким образом, для уравнения(43) выполнены условия определения
линейной функции. Как было показано в предыдущем параграфе, в этом
случае уравнение (43) имеет единственное решение:
.
Таким образом, для уравнения(43) выполнены условия определения
линейной функции. Как было показано в предыдущем параграфе, в этом
случае уравнение (43) имеет единственное решение: ![]() .
.
Так как функциональное уравнение (43) имеет единственное решение
![]() и каждой функции
и каждой функции ![]() соответствует единственная функция
соответствует единственная функция![]() ,
то функциональное уравнение (43) при условиях 1), 2) имеет
единственное решение. Это единственное решение уравнения (43) можно
положить в основу определения логарифмической функции. Так как
,
то функциональное уравнение (43) при условиях 1), 2) имеет
единственное решение. Это единственное решение уравнения (43) можно
положить в основу определения логарифмической функции. Так как
![]() ,
, ![]() и поэтому можно считать, что
и поэтому можно считать, что ![]() , известно, что
, известно, что![]() ,
значит,
,
значит, ![]() .
.
Возможен второй способ доказательства. Для доказательства
единственности решения функционального уравнения рассмотрим
произвольное решение ![]() и введем замену переменных. Заменяя
и введем замену переменных. Заменяя ![]() на
на ![]() по формуле
по формуле![]() ,
получим
,
получим ![]() . Аналогично
. Аналогично ![]() , то есть
, то есть ![]() . При этом
. При этом ![]() . С новой функцией уравнение (43) примет вид
. С новой функцией уравнение (43) примет вид ![]() функционального уравнения, определяющего линейную функцию при
известных условиях. При этом функция
функционального уравнения, определяющего линейную функцию при
известных условиях. При этом функция ![]() непрерывна как композиция двух непрерывных функций и
непрерывна как композиция двух непрерывных функций и ![]() .
.
Таким образом, для уравнения(43) выполнены условия определения
линейной функции. Как было показано в предыдущем параграфе, в этом
случае уравнение (43) имеет единственное решение: ![]() .
.
Определение 7 . Решение класса функциональных уравнений (43)
называется логарифмической функцией и обозначается ![]()
![]() при выполнении условий 1) - 3).
при выполнении условий 1) - 3).
2.4 Определение степенной функции
Напомним свойства степени с одинаковым
показателем.![]()
(45)
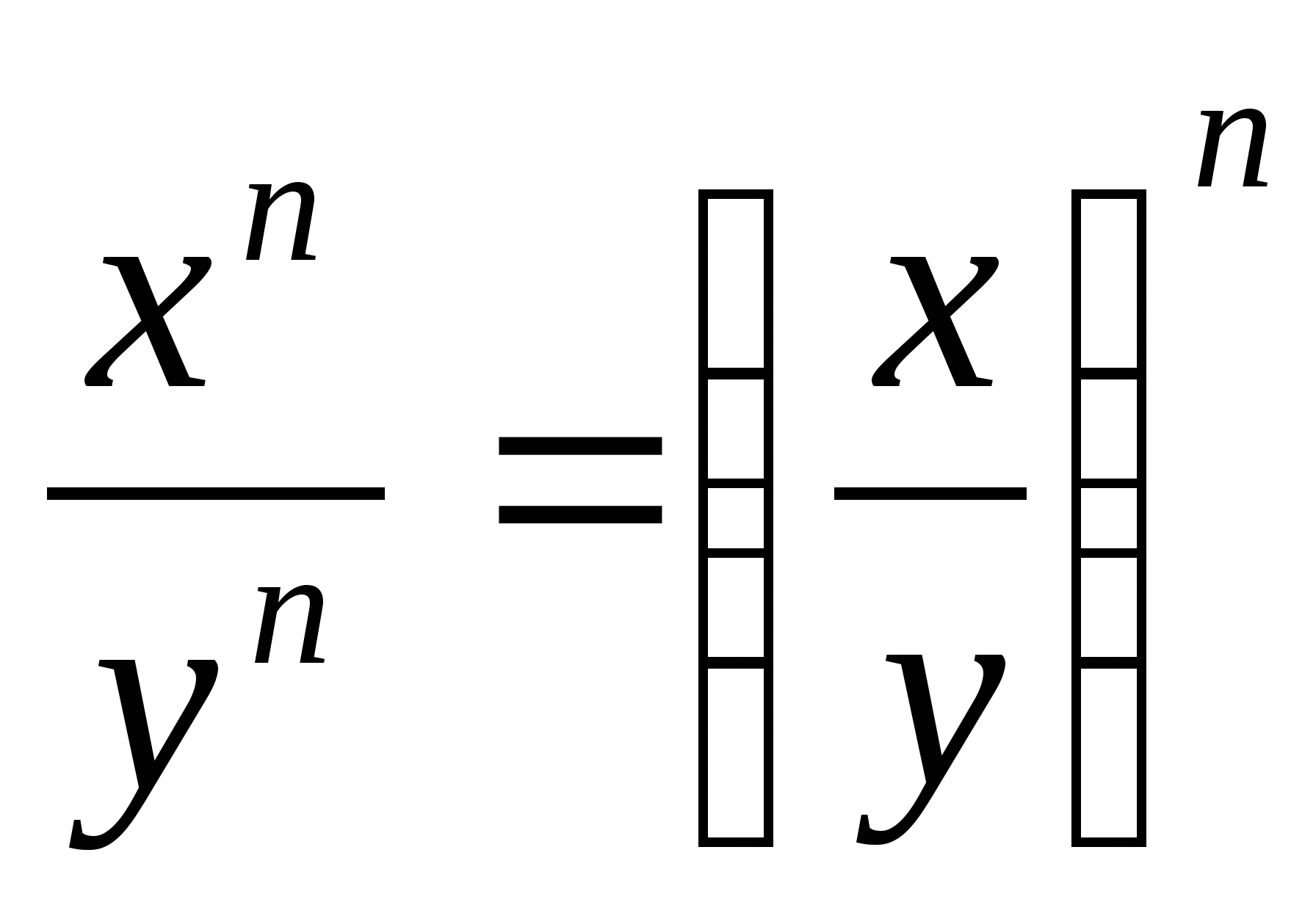
(46)
Составим соответствующие функциональные уравнения
(47)
![]()
(48)
Докажем эквивалентность полученных уравнений.
Рассмотрим функциональное уравнение (47) при условиях:
-
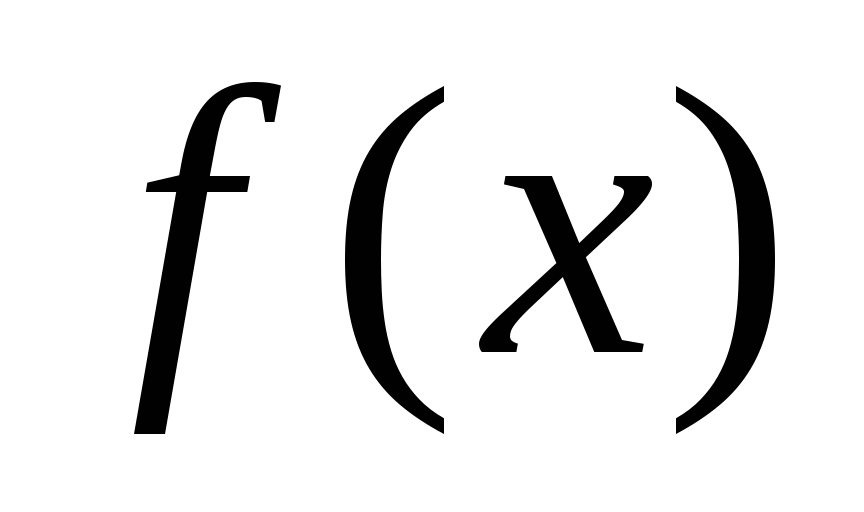 -
непрерывная функция в интервале
-
непрерывная функция в интервале 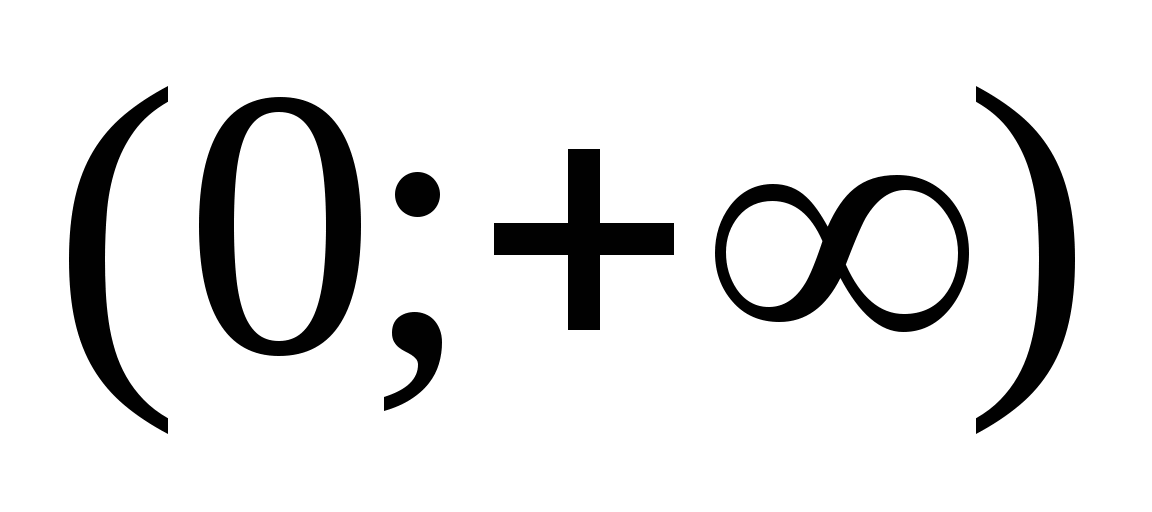 и отличная от постоянной.
и отличная от постоянной.
-
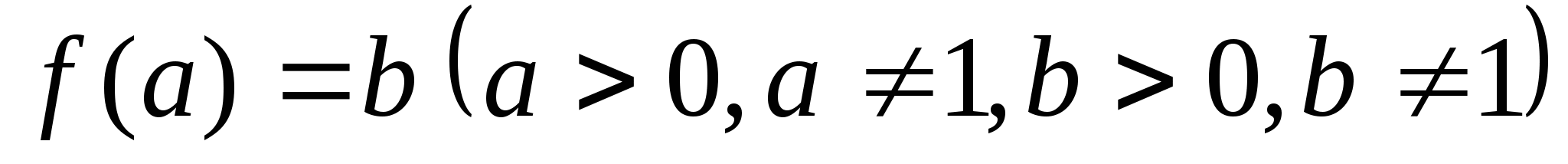 .
.
Теорема 4. Класс уравнений (47) при условиях 1), 2) имеет единственное решение.
Доказательство. Заменим независимые переменные ![]() и
и ![]() новыми переменными
новыми переменными ![]() и
и ![]() по формулам
по формулам ![]() , а
, а ![]() и введем в рассмотрение функцию
и введем в рассмотрение функцию ![]() .
.
Тогда из уравнения (47) следует: ![]() , то есть функция
, то есть функция ![]() удовлетворяет функциональному уравнению.
удовлетворяет функциональному уравнению.
![]() и
условию
и
условию ![]() (
(![]() )
)
Как было показано, единственным непрерывным решением этого
уравнения при указанных условиях является показательная
функция![]() .
.
Следовательно, единственным непрерывным решением уравнения (47)
будет функция ![]() .
.
Таким образом, ![]() , где
, где ![]() .
.
Определение 8. Непрерывное в интервале ![]() решение класса функциональных уравнений (47) при условиях 1), 2)
называется степенной функцией и обозначается
решение класса функциональных уравнений (47) при условиях 1), 2)
называется степенной функцией и обозначается ![]() .
.
Исследуем свойства решений класса функциональных уравнений.
а) ![]() . Действительно, полагая в уравнении
. Действительно, полагая в уравнении ![]() , получим
, получим ![]() . Отсюда или
. Отсюда или ![]() , или
, или ![]() . Но если
. Но если ![]() , то при любом
, то при любом ![]() ,
, ![]() . действительно, пусть
. действительно, пусть ![]() . Тогда
. Тогда ![]() . Следовательно,
. Следовательно, ![]() и
и ![]() .
.
б) ![]() , так как
, так как ![]() , то
, то ![]() .
.
г) Если ![]() , то
, то ![]() . Докажем, что если
. Докажем, что если ![]() ,то
,то ![]() . Предположим противное. Пусть
. Предположим противное. Пусть ![]() и
и ![]() . Но тогда для любого
. Но тогда для любого ![]() . Имеем:
. Имеем: 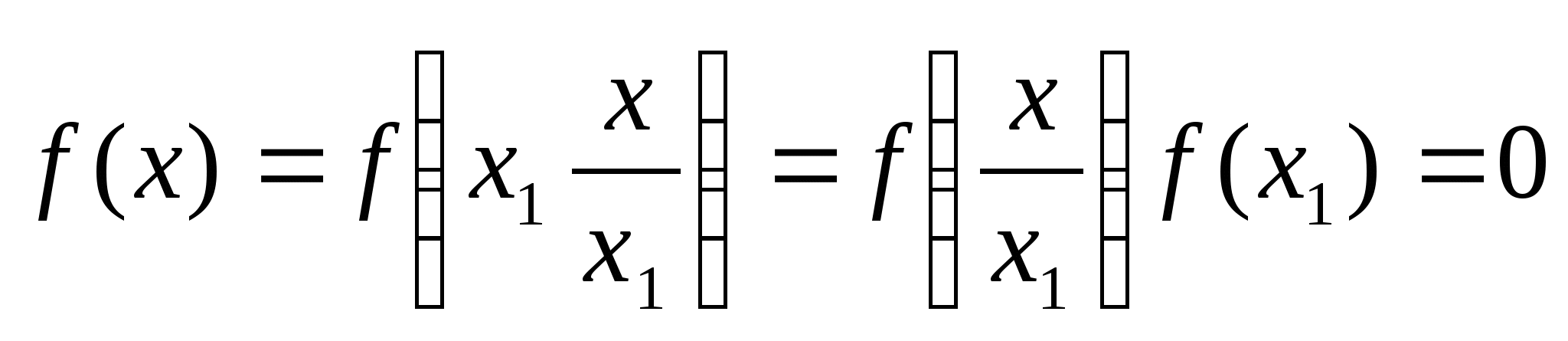 ,чтo невозможно, так как, по условию 1), функция отлична от
постоянной.
,чтo невозможно, так как, по условию 1), функция отлична от
постоянной.
д) Все значения функции ![]() положительны. Так как
положительны. Так как ![]() , то все значения положительны.
, то все значения положительны.
е) Если![]() ,
то
,
то![]() .
Докажем, что если
.
Докажем, что если ![]() , то
, то ![]() . Предположим противное. Пусть для некоторого
. Предположим противное. Пусть для некоторого ![]()
![]() .
Но тогда
.
Но тогда ![]() . Из равенства
. Из равенства ![]() имеем
имеем ![]() и, следовательно,
и, следовательно, ![]() .
.
Далее, из равенства ![]() получаем
получаем ![]() и, значит,
и, значит, ![]() . Наконец,
. Наконец,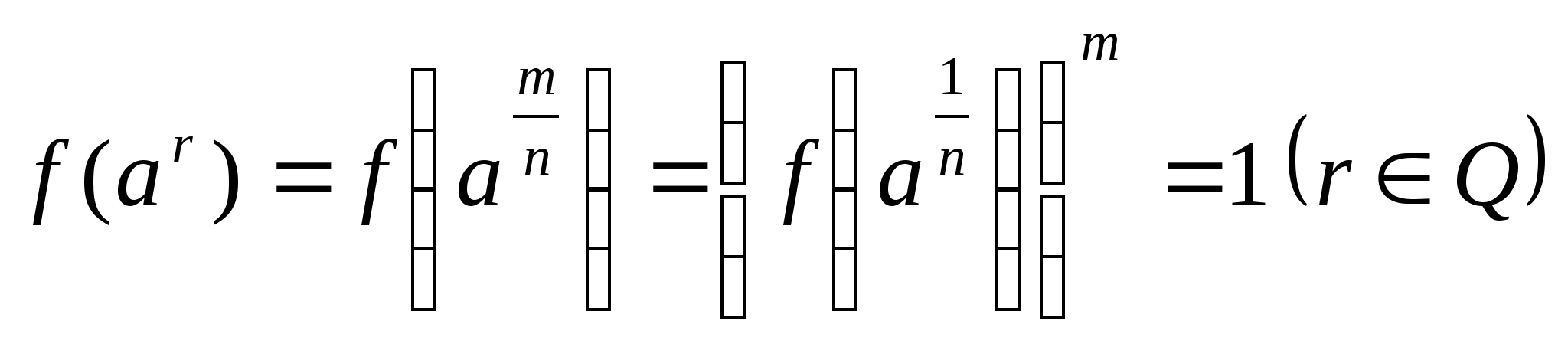 .
Но тогда для любого действительного
.
Но тогда для любого действительного ![]() найдется последовательность
найдется последовательность ![]() рациональных чисел, сходящаяся к
рациональных чисел, сходящаяся к ![]() в силу непрерывности
в силу непрерывности ![]() , что невозможно, поэтому
, что невозможно, поэтому ![]() .
.
Таким образом, мы рассмотрели основные элементарные функции, сформулировали определение элементарных функций с помощью функциональных уравнений.
Заключение
Проделав большую работу по изучению функциональных уравнений,
приходим к такому выводу, что функциональное уравнение -
это уравнение, в котором неизвестными являются функции (одна или
несколько). Например, ![]() ,
, ![]() .
.
Решить функциональное уравнение - значит, найти неизвестную функцию, при подстановке которой в исходное функциональное уравнение оно обращается в тождество (если неизвестных функций несколько, то необходимо найти их все).
Соотношения, задающие функциональные уравнения, являются тождествами относительно некоторых переменных, а уравнениями их называют потому, что неизвестные функции - искомые.
Многие функциональные уравнения содержат несколько переменных. Все эти переменные, если на них не наложены какие-то ограничения, являются независимыми.
Всегда четко должно быть оговорено, на каком множестве функциональное уравнение задается, т.е. какова область определения каждой неизвестной функции. Общее решение функционального уравнения может зависеть от этого множества.
Кроме области определения функций, важно знать, в каком классе функций ищется решение. Количество и поведение решений очень строго зависит от этого класса.
Вообще для функциональных уравнений, не сводящихся к дифференциальным или интегральным, известно очень мало общих методов решения. Мы рассмотрели основные приемы, помогающие найти решения таких уравнений.
В результате проведенных исследований можно сделать вывод , что термин функциональные уравнения обычно используются для уравнений, несводимых простыми способами к алгебраическим уравнениям. Не зная методов их решения, решить их практически невозможно.
Вопросы, рассмотренные в работе, не только расширяют кругозор, но и несут обучающую функцию, что только подчеркивает значимость выбранной темы.
Список использованных источников
1. Просветов Г.И. Функциональные уравнения: задачи и решения: Учебно-практическое пособие. - М.: Издательство «Альфа-Пресс», 2010. - 48с.
2. Функциональный анализ, Л.В.Канторович, Г.П.Акилов, издание второе, Главная редакция физико-математической литературы изд-ва «Наука», М., 1977г.
3. Элементарные функции: учебно-методическое пособие/ сост. О.Н.Зубкова; Ряз.гос.ун-т им.С.А.Есенина.- Рязань, 2008.- 84с.
4. www.cleverstudents.ru/functions/basic_elementary_functions.html
</
36