Методическая разработка урока 'Симметрия вокруг нас' 8 класс.

Учитель математики ГОУ школы №103

Санкт-Петербурга

Рогачева Татьяна Викторовна

Мультимедийный урок: «Симметрия вокруг нас».

(Рекомендовано для проведения в 6, 8 классах)

Цели: 1. Образовательные: провести исследовательские работы по изучению явлений симметрии и сформулировать понятия осевой и центральной симметрий в природе, архитектуре и технике;

2. Развивающие: развитие логического мышления, творческой активности, познавательного интереса;

2. Воспитательные: воспитание умения сплоченно и дружно работать в коллективе, внимательно слушать речь других, приобретение навыков самостоятельной работы.

Оборудование:

мультимедийная аппаратура, раздаточный материал: задания с лабораторной работой, карточки с исследовательскими задачами.

Учащиеся разбиваются на группы по 4-5 чел.

ХОД УРОКА.

1. Актуализация опорных знаний учащихся.

Вопрос учащимся:

Какие вы знаете виды симметрии?

Ожидаемый ответ: Симметрия относительно точки (центральная) и симметрия относительно прямой (осевая).

Вопрос учащимся: Когда точки А и В будут симметричны относительно точки О? (слайд №3)

Ожидаемый ответ:

«Точки А и В симметричны относительно точки О, если О является серединой отрезка АВ». А •

О•

•В

Вопрос учащимся: Когда точки А и В будут симметричны относительно прямой m?(слайд №4)

Ожидаемый ответ: Точки А и В симметричны относительно прямой m, если m является серединным перпендикуляром для отрезка АВ.

А •

О

m •В

2. Изучение нового материала.

Беседа учителя:

Сегодня мы прикоснемся к удивительному математическому явлению - симметрии. В древности слово «симметрия» употреблялось как «красота», «гармония».

Термин «гармония» в переводе с греческого означает «соразмерность, одинаковость в расположении частей».

Известный немецкий математик нашего столетия Герман Вейль дал определение симметрии таким образом: «Симметрия является той идеей, с помощью которой человек веками пытается объяснить и создать порядок, красоту и совершенство».

Принцип симметрии играет важную роль в математике, архитектуре, он встречается в живой природе.

Слайд 4, 5, 6. Посмотрите внимательно на рисунки. Что вы на них увидели? Как расположены эти фигуры?

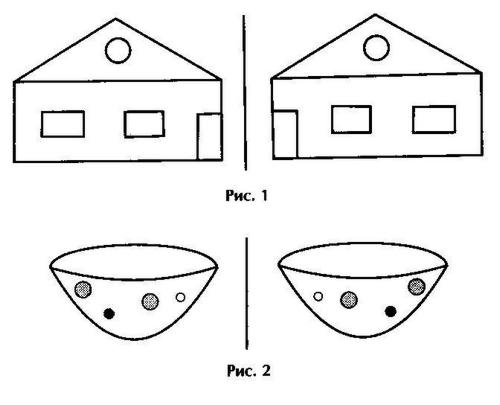
Такие фигуры называются симметричными, а прямую, разъединяющую эти фигуры - осью симметрии.

Если согнуть лист по этой прямой, то эти фигуры полностью совпадут и мы сможем видеть только одну фигуру.

А как же получить симметричные фигуры?

Задание №1.

(самый простой способ получения симметричных фигур)

Каждая группа имеет лист бумаги.

Возьмите лист бумаги и перегните его пополам. Теперь разверните и на одной стороне постройте треугольник (прямоугольник, ромб, квадрат). Далее сложите лист по линии сгиба и проколите вершины данной фигуры так, чтобы были проколоты обе половинки. Теперь разверните лист и соедините по линейке полученные точки-дырочки. Таким образом, мы с вами построили фигуры, симметричные данным относительно прямой (линии перегиба). Убедитесь в этом. Для этого сложите лист по линии сгиба и посмотрите через него на свет.

Что вы видите? (Фигуры совпали).

Это самый простой способ построения симметричных фигур.

Задание №2.

Используя определение точек, симметричных относительно прямой, постройте с помощью линейки и карандаша фигуру, симметричную заданной. (Слайд №9)

(Проверяем работу каждой группы).

Вывод:

Чтобы построить геометрическую фигуру, симметричную данной относительно некоторой прямой, надо построить точки, симметричные значимым точкам (вершинам) данной фигуры относительно этой прямой и потом соединить эти точки отрезками.

Есть фигуры, которые имеют свою ось симметрии. Например, (слайд 10).

Задание №3.

Одна группа

берет лист бумаги. Согнув его пополам, вырезают из него какую-нибудь фигуру, но так, чтобы линию перегиба не повредить.

Вторая группа

берет салфетку, сложенную вчетверо, и вырезают снежинку.

Внимательно рассмотрим результаты работы.

Линия сгиба вырезанной фигуры делит её на две равные части. Такая фигура называется симметричной относительно прямой (линии сгиба), а линия сгиба - осью симметрии.

Рассмотрим снежинку. Сколько в ней получилось линий сгиба (осей симметрии)?

Итоги: если внимательно рассмотреть фигуры, то среди них есть фигуры, имеющие одну или несколько осей симметрии. А есть фигуры, которые вообще не имеют осей симметрии.(Слайд №12)

Задание №3. (Слайд №13)

Набор геометрических фигур

(лежит у каждой группы на столе)

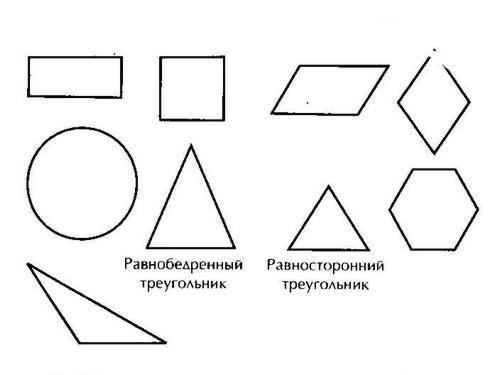
Работая совместно в группах, вы, сгибая данные фигуры любым доступным способом, постарайтесь совместить половинки фигур друг с другом.

В процессе работы вы должны определить:

1. Какие фигуры обладают симметрией, а какие нет;

2. Количество осей симметрии у каждой фигуры;

3. Какая фигура имеет наибольшее количество осей симметрии.

После выполнения данного задания, анализируем результаты.

Во всех рассмотренных случаях мы имели дело с симметрией, которая называется осевой, так как данные фигуры симметричны (расположены одинаково) относительно прямой (оси).

Но ведь существуют и другие виды симметрии: центральная, зеркальная.

Сегодня мы подробнее остановимся на зеркальной симметрии. Если поставить зеркало вдоль оси симметрии фигуры, обладающей осевой симметрией, то мы увидим, что отраженная в зеркале половинка фигуры дополняет её до целой фигуры. (работа с зеркалом)

Прямая, к которой приставлено зеркало, называется осью симметрии.

А знаете ли вы, что не только геометрические фигуры имеют ось симметрии. Если внимательно присмотреться к печатным буквам нашего алфавита, то можно увидеть, что некоторые из них обладают осевой симметрией. Например, буква «Н» имеет и горизонтальную и вертикальную оси симметрии.

Задание №5. (Слайд №15)

Перед вами на столах алфавит. С помощью зеркала определите, какие из букв имеют горизонтальную, а какие вертикальную симметрию, какие вовсе не имеют симметрии. (В результате учащиеся заполняют таблицу).

Таблица (слайд №16)

Буквы, имеющие горизонтальную ось симметрии

Буквы, имеющие вертикальную ось симметрии

Буквы, не имеющие ось симметрии

Буквы, имеющие горизонтальную и вертикальную оси симметрии

В Е Ж З К Н О С A Х Э Ю

А Д Ж Л М Н О П Т A Х Ш

Б Г И Р У Ц Ч Я Щ

Ж Н О Х Ф

Примечание: Буквы «Л» и «Д» в другом шрифте имеют ось, поэтому их лучше написать от руки.

(Слайд №17, №18)

Из букв, которые обладают горизонтальной осью симметрии, можно составить слова, которые тоже будут обладать горизонтальной симметрией. Например: КОФЕ, ЗОВ.

Предлагаю провести игру: Из букв, обладающих горизонтальной симметрией, составьте

• Слова, которые также будут обладать горизонтальной симметрией. Кто больше составит слов?

• Слова, которые обладают вертикальной симметрией? Например: шалаш, потоп.

Переходим к симметрии в пространстве. Только там вместо оси симметрии - плоскость симметрии. (демонстрация пространственных фигур: шар, куб. (см. презентацию Слайд №19 - №21))

Симметрия широко распространена в природе (жуки, бабочки, листья деревьев) Слайд презентации.

Симметрия, характерная для представителей животного мира, называется билатеральной симметрией. (Слайд №26)

Применение симметрии в архитектуре. (Слайд №24-№30)

Итог занятия:

Учащиеся должны ответить на вопросы:

1. С каким понятием мы познакомились?

2. Какие виды симметрии вы запомнили?

3. Что нового вы узнали?

В процессе каждая группа предоставляла результаты по выполнению каждого задания, на основании которого будут выставлены оценки.