Урок по математике для 5 класса «Сложение смешанных чисел, дробные части которых имеют одинаковые знаменатели»

Учитель математики: Новоселова Татьяна Михайловна.

Технология: проблемно-диалогического обучения.

Тема урока: Сложение смешанных чисел, дробные части которых имеют одинаковые знаменатели. 5 класс.

Цель: Самостоятельно сформулировать правило сложения смешанных чисел, дробные части которых имеют одинаковые знаменатели.

Новое знание: Ответ на вопрос: как найти сумму смешанных чисел, дробные части которых имеют одинаковые знаменатели.

Тип знания: правило.

Результат: Сформулировали правило сложения смешанных чисел, дробные части которых имеют одинаковые знаменатели.

План урока:

1. Постановка проблемы - 5 мин

2. Поиск решения - 22 мин

3. Выражение решения - 5 мин

4. Реализация продукта - 8 мин

Этап

Анализ

Учитель

Ученик

П

О

С

Т

А

Н

О

В

К

А

П

Р

О

Б

Л

Е

М

Ы

1. Возникновение проблемной ситуации: практическое задание, не сходное с предыдущим (тип: с затруднением)

Устная работа. (на доске записаны задания)

Выполните действия:

а) ;

б) ;

в) ;

г) ;

д) =?

=?

=;

=;

=;

=;

Предлагают варианты ответов.

2. Побуждение к осознанию противоречия

- Вы смогли выполнить задание?

- Почему не получается?

- Чем это задание не похоже на предыдущие?

- Уточните, каких смешанных чисел?

- Какой возникает вопрос?

- Нет.

- Мы умеем складывать дроби с одинаковыми знаменателями, дроби и натуральные числа.

- Надо найти сумму смешанных чисел?

- Дробные части которых имеют одинаковые знаменатели.

- Как найти сумму смешанных чисел, дробные части которых имеют одинаковые знаменатели?

Этап

Анализ

Учитель

Ученик

П

О

И

С

К

Р

Е

Ш

Е

Н

И

Я

1. Побуждение к выдвижению гипотез

2. Принятие выдвигаемых учениками гипотез.

- Догадайтесь, как можно найти сумму данных смешанных чисел? Какие есть гипотезы (предположения)?

- Так, еще гипотезы?

- Какие еще есть предположения?

( Гипотезы фиксируются на доске)

- Отдельно сложить целые части и отдельно сложить дробные части.

- Можно обратить смешанные числа в неправильные дроби и их сложить.

- Изобразить смешанные числа и по рисунку найти их сумму. (например, на числовой прямой)

3. Побуждение к проверке гипотез.

- Это гипотезы, но чтобы узнать, какая из них верна и какой именно мы будем пользоваться при сложении, что нам надо сделать?

- Как нам проверить эти гипотезы?

- Сейчас вы будете работать в группах.

Каждая группа проверяет 1 гипотезу. (Распределяю)

Соблюдайте «Требования к работе в малых группах» (памятка), а также обратите внимание на памятку «Составление плана устного ответа»

Продумайте записи, которые вам нужны будут при ответе.

(Оформляют маркерами на листах А3)

- Все гипотезы проверить

- Применить гипотезы к данным примерам

Делятся на группы.

Этап

Анализ

Учитель

Ученик

П

О

И

С

К

Р

Е

Ш

Е

Н

И

Я

4. Принятие предлагаемых учениками проверок

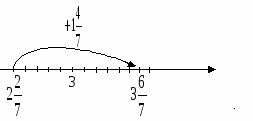
- Первым отвечает представитель от группы, в которой складывали смешанные числа по рисунку

- Выскажите свое отношение к данному способу сложения

3

- Нерациональный способ

5. Вывод

- Следующий представитель от группы

- Итак, представляем последнюю гипотезу.

- Сравните эти два способа сложения. Какой вам больше нравится и почему?

- Значит, как надо складывать смешанные числа, дробные части которых имеют одинаковые знаменатели?

- 2 способ тоже нерациональный, так как лишние шаги: 1) обращение смешанных чисел в неправильные дроби; 2) в результате получится неправильная дробь, значит надо выделить целую часть.

3 способ сразу позволяет найти сумму смешанных чисел.

- Чтобы найти сумму смешанных чисел, дробные части которых имеют одинаковые знаменатели, нужно сложить отдельно целые части и дробные части. Если при сложении получилась неправильная дробь, надо выделить из нее целую часть и добавить к уже имеющейся целой части.

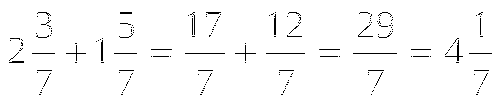
Требования к работе в малых группах.

1. Распределите обязанности (роли) в группе:

• Ответственный - отвечает за то, чтобы все ученики поняли суть работы и выполняли ее ответственно.

• Наблюдатель - следит, чтобы работали все.

• Секретарь - ведет записи обсуждений, оформляет решения, отчет группы, «карточку оценок и взаимооценок».

• Выступающий - презентует совместно полученный результат работы в группе.

• Кто держит задание - напоминает, о чем спрашивается.

2. Обсудите проблему, поставьте цель, наметьте пути решения проблемы, выполните намеченные действия на практике, представьте, полученный результат, в удобном для восприятия виде.

3. При обсуждении соблюдайте коммуникативные нормы:

• Перескажи текст своими словами;

• Восстанови смысл:

«Ты считаешь, что…?»

( «Правильно ли я тебя понял, ты говорил, что…?»);

• Квалифицируй свои действия:

«Я тебе возражаю»,

«Я с тобой согласен».

3. Каждый в группе должен знать решение и уметь его объяснить.

3. Провести рефлексию работы каждого и группы в целом.

3. При обсуждении группы не должны мешать друг другу.

Составление плана устного ответа

1. Выделить понятия, которым нужно дать определение.

2. Выделить правило, которое нужно сформулировать и доказать.

3. Выделить определения, правила, на которые нужно сослаться при доказательстве.

4. Составить план доказательства.

5. Продумать записи на доске во время ответа.

6. Показать, где и как применяется правило.

7. Сделать выводы.