Конспект урока по математике на тему Отношения чисел и величин ФГОС(: класс)

ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА

ДАТА ПРЕДМЕТ математика УРОК № 4 КЛАСС 6

ХОД УРОКА:1. Организационный момент.

Учитель приветствует учащихся, настраивает на урок

Включаются в деловой ритм урока

2. Мотивация учебной деятельности

Вспомним задачи «на части».

Для варенья из малины на 2 части ягод берут 3 части сахара. Сколько сахара необходимо взять на 2 кг 800 г ягод?

Говорят, что ягоды и сахар взяты в отношении 2 к 3.

Записывают: 2 : 3 или .

Предложить учащимся сформулировать тему и цель урока.

Решают задачу.

Формулируют (уточняют) тему урока и учебную задачу

3. Актуализация знаний.

1. Когда говорят, что натуральное число а делится нацело на натуральное число b?

2. Как называются компоненты при делении?

3. Как найти неизвестное делимое? А делитель?

4. На какие числа делится нацело любое число?

5. Можно ли делить на нуль? А если разделить нуль на любое число?

Отвечают на вопросы

4. Организация познавательной деятельности. Изучение нового материала.

Отношение чисел и величин.

Определение. Частное двух не равных нулю чисел а и b называют еще отношением чисел а и b.

Запись: или .

Числа а и b называют членами отношения.

Пример 1. Используя слово «отношение», прочитайте запись:

1) (отношение числа 15 к числу 3);

2) (отношение числа 2 к числу 7);

3) 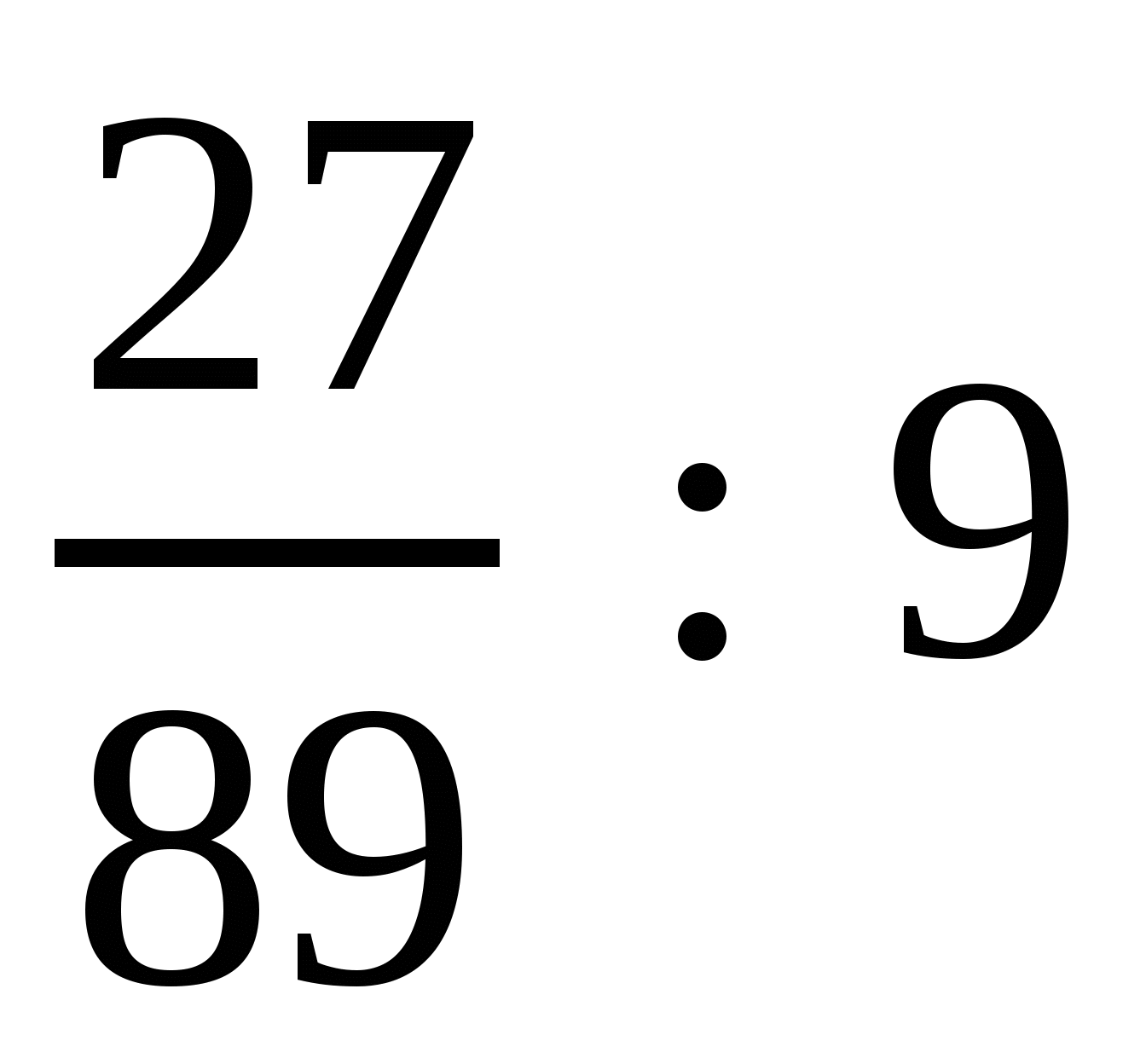(отношение числа к числу 9).

Пример 2. Найдите отношение:

1) ;

2), ;

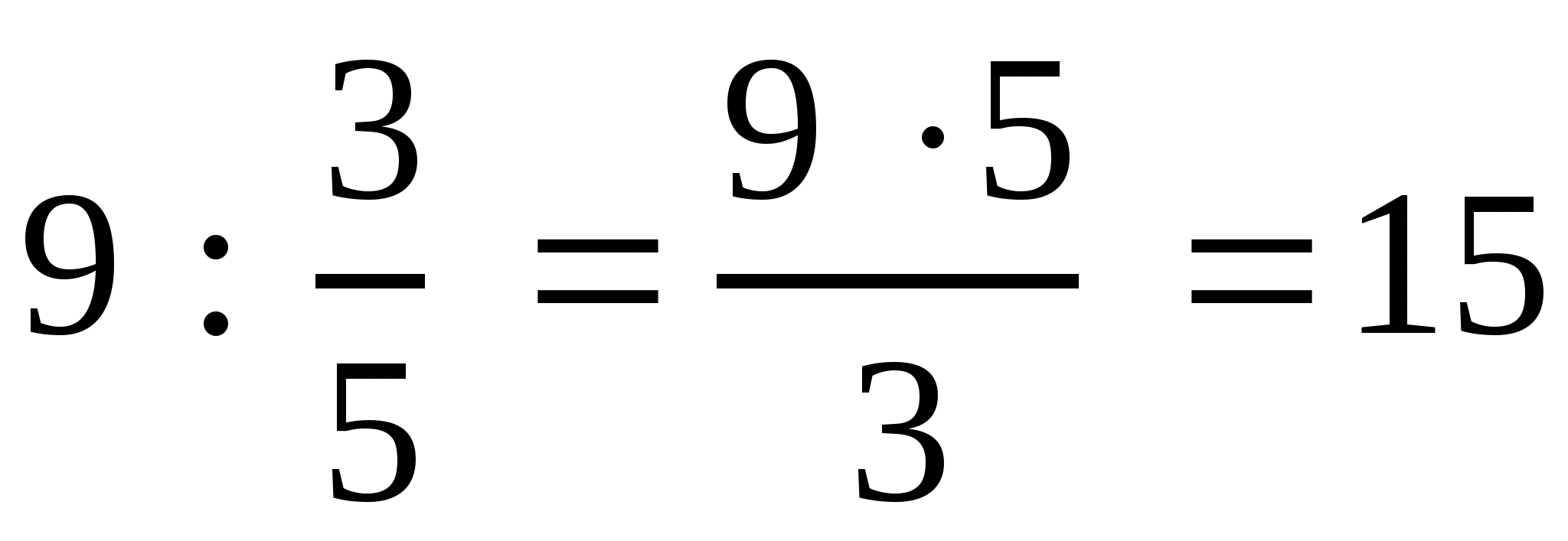3) .

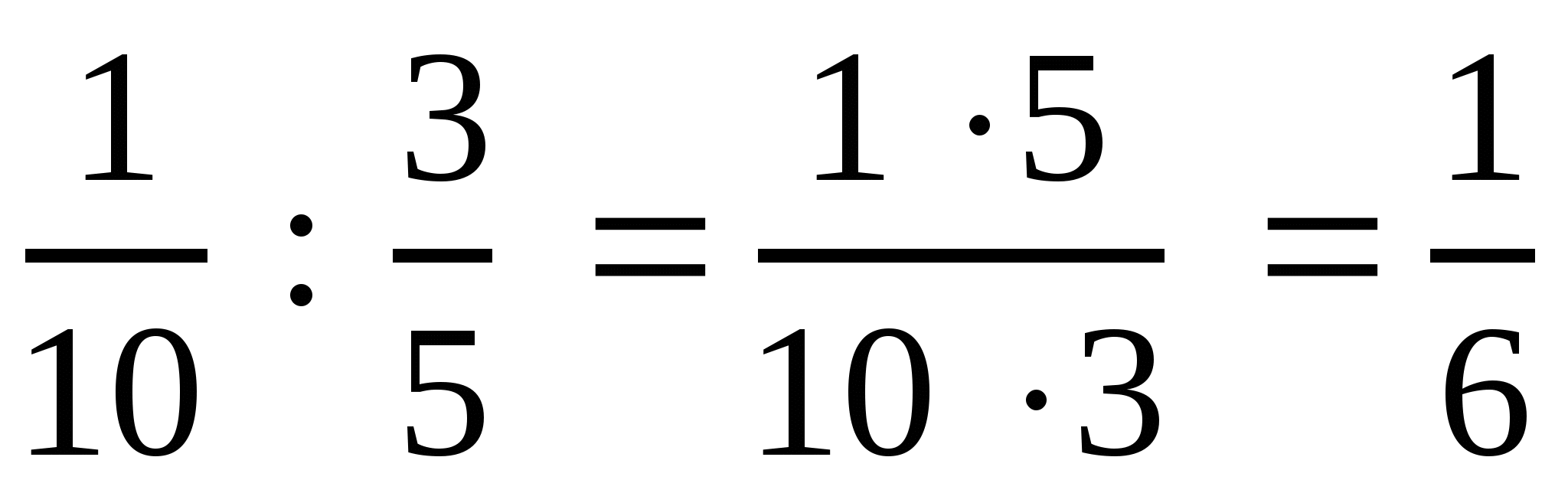Вспомним основное свойство частного.

Свойство частного. Делимое и делитель можно умножить или разделить нацело на одно и то же натуральное число - частное от этого не изменится.

.

Из основного свойства частного следует свойство отношения.

Свойство отношения. Отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю.

;

.

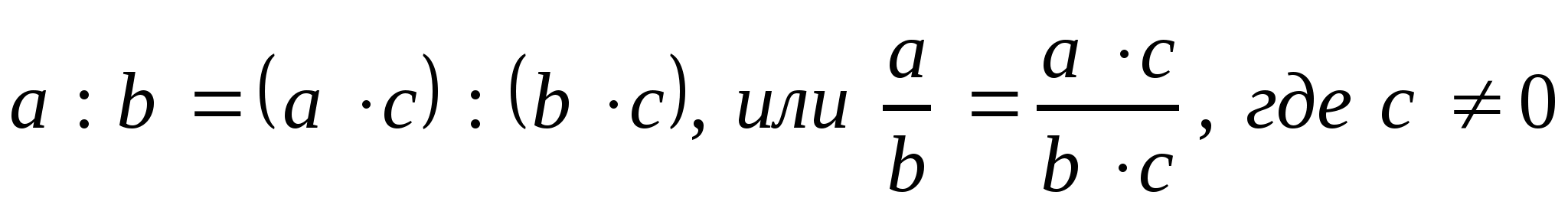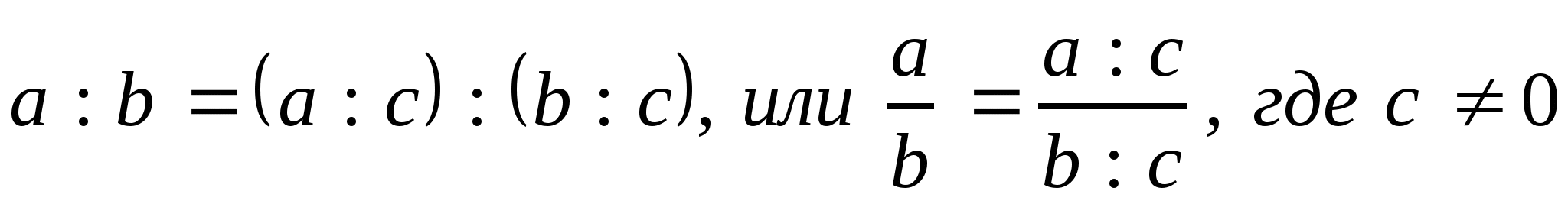Пример 3. Упростить отношение а) 12: 8; б)

Определение. Частное двух величин называется отношением этих величин.

Сами величины называют членами отношения.

Отношение величин одного наименования (длин, скоростей, стоимостей и т.д., выраженных одинаковыми единицами измерения) есть число.

Такие величины называют однородными.

Пример 4. Найдите отношение величин:

1) ; 2) .

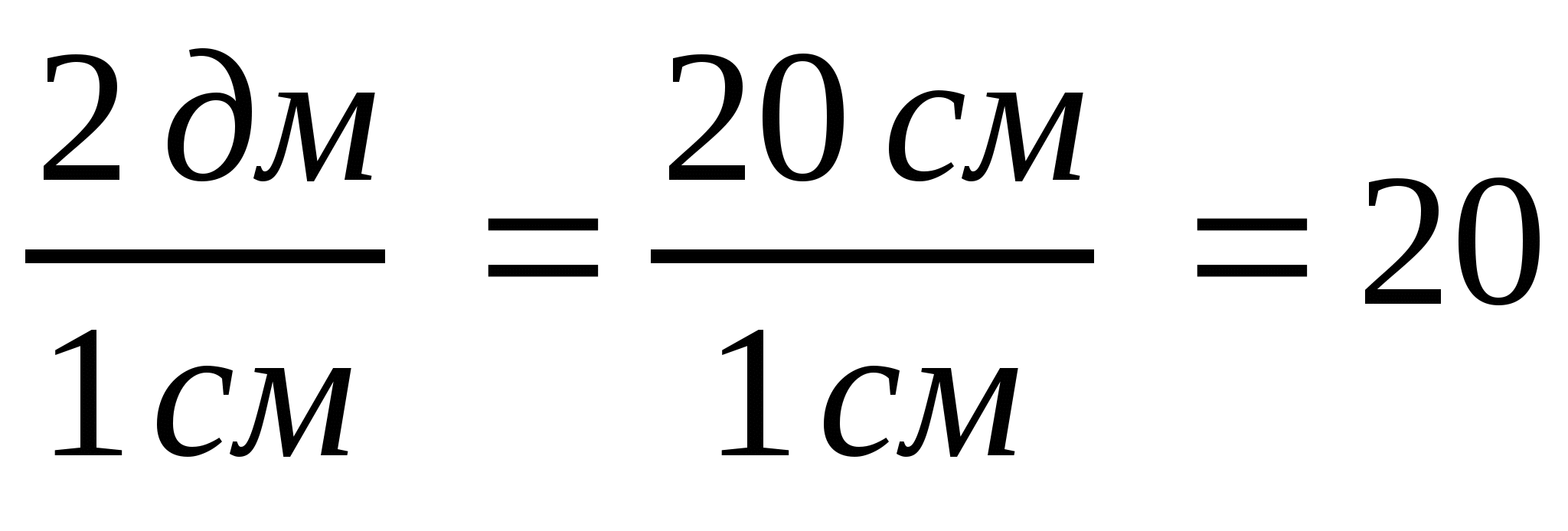Отношение однородных величин показывает во сколько раз одна величина больше другой.

Отношение величин разных наименований (пути и времени 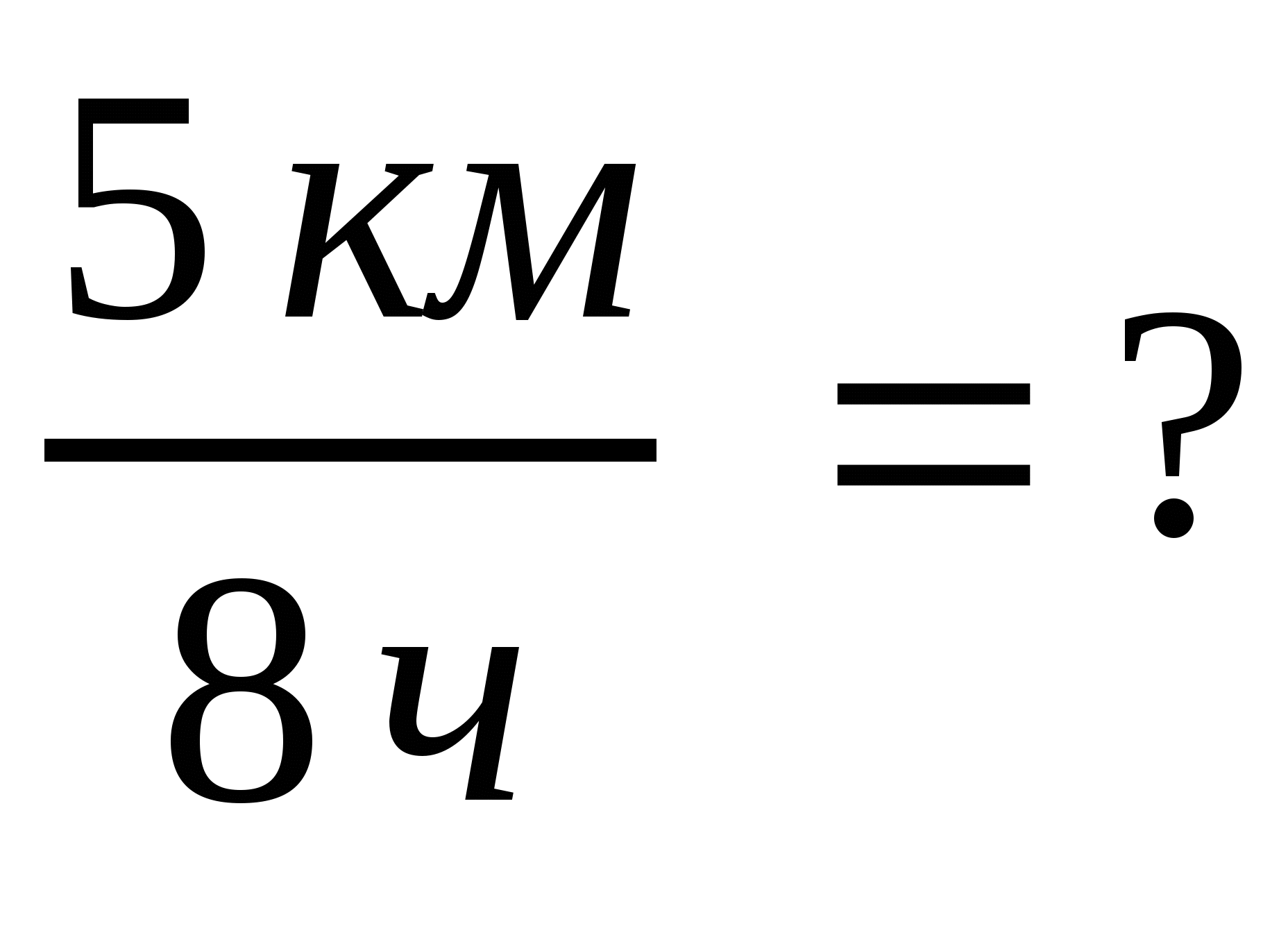, стоимости товара и его количества 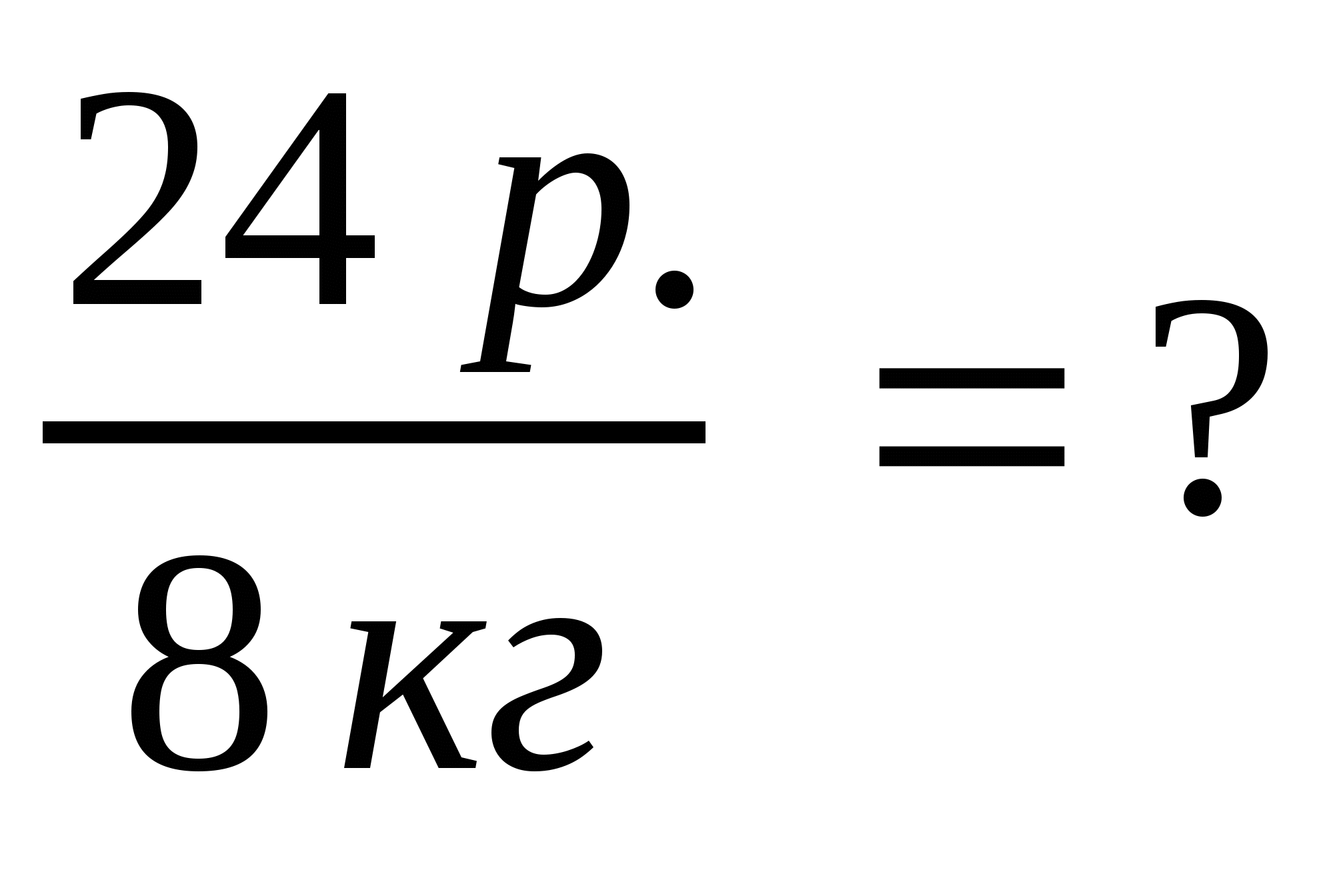, массы тела и его объема 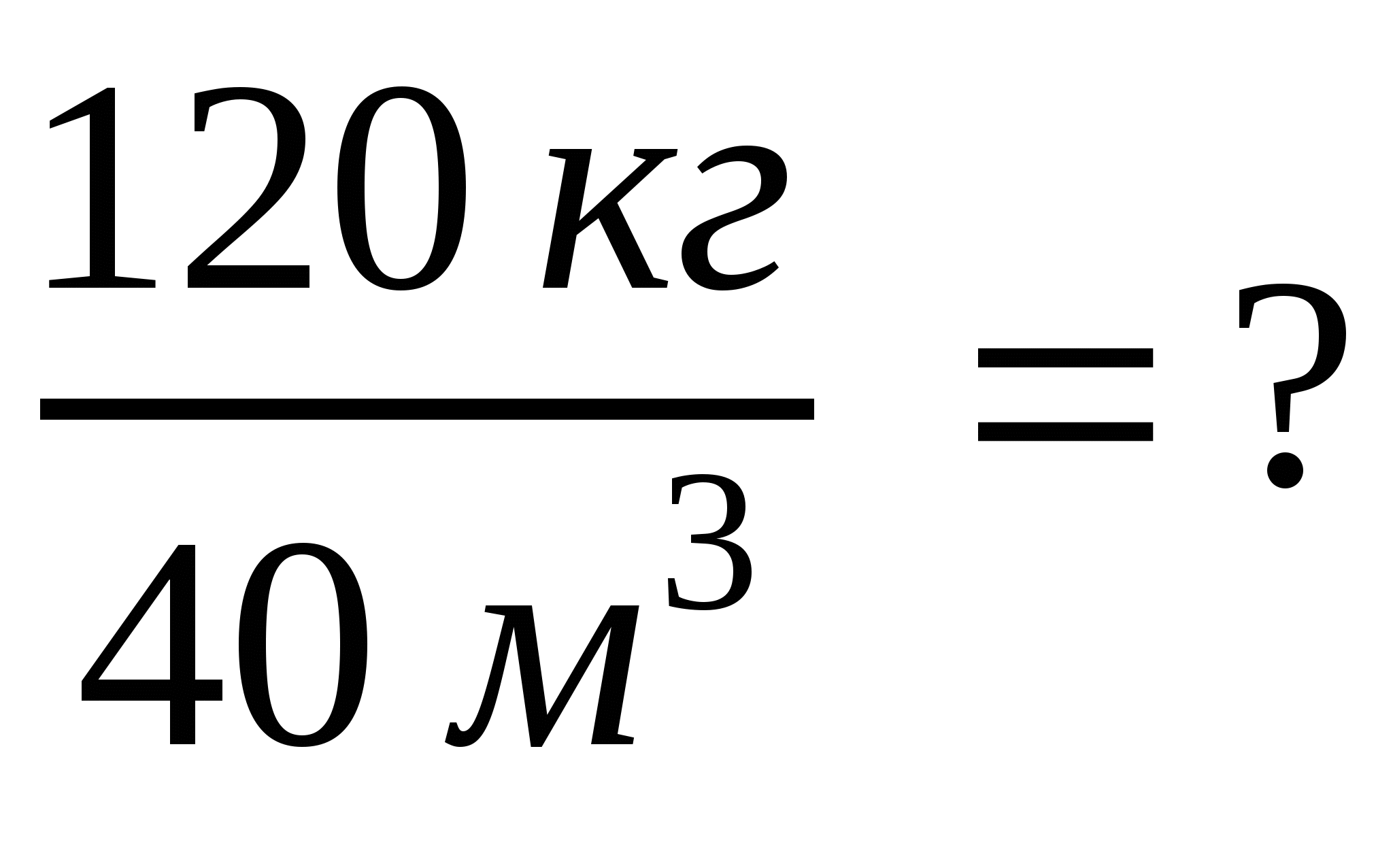и т.д.) есть новая величина.

Отношение величин в математике.

Отношение пути (км) к времени (ч) есть новая величина - скорость, выраженная в единицах скорости (км/ч). .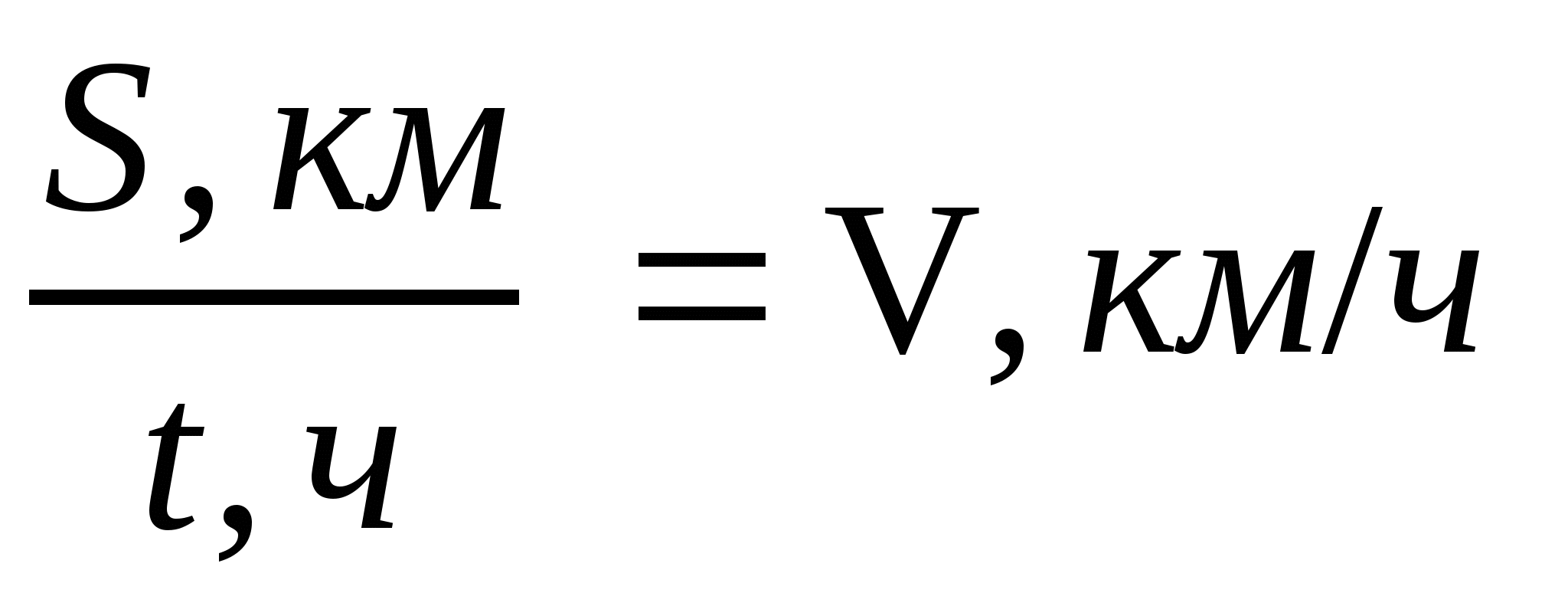

Пример 5. Найдите отношение пути (16 км) к времени (8 ч):

.

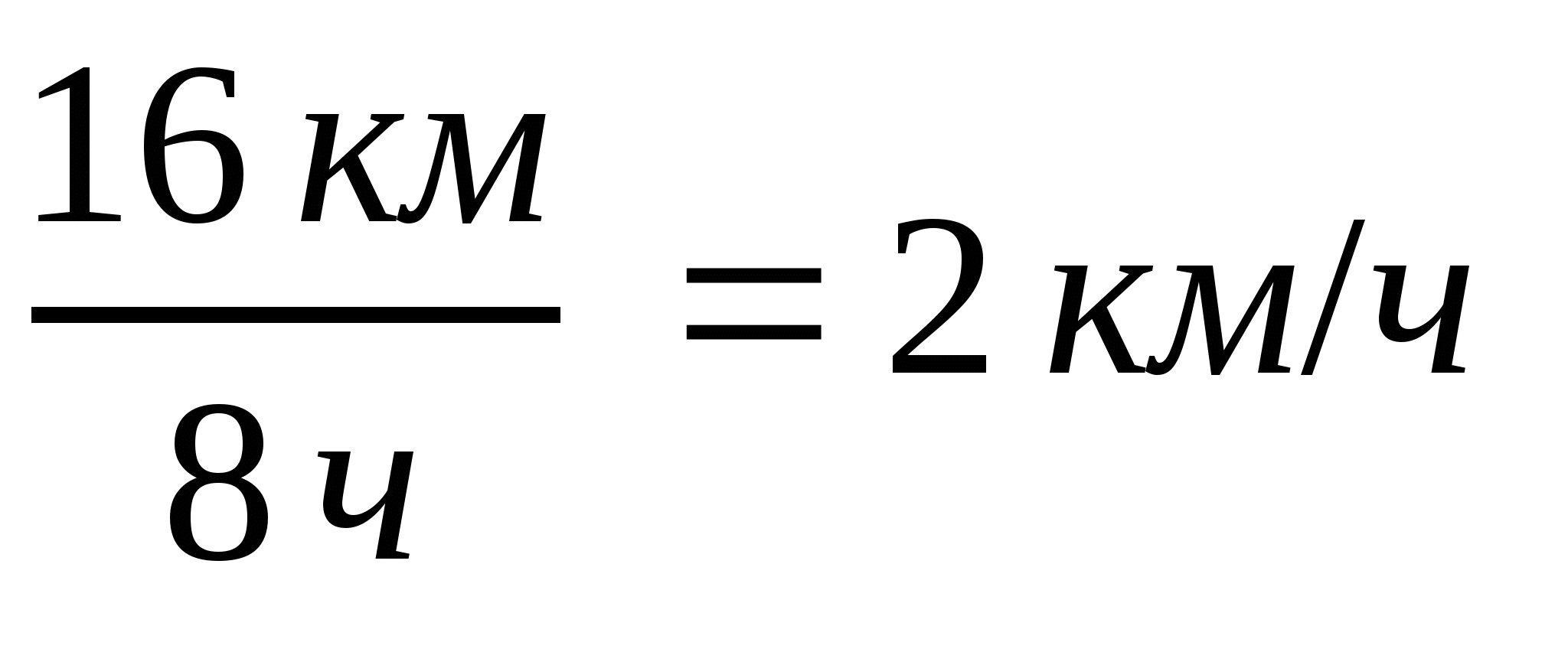Отношение стоимости товара (р.) к его массе (кг) есть новая величина - цена, выраженная в единицах цены (р./кг). .

Знаменатель в единицах цены обычно не пишут, а пишут и говорят «цена 1 кг товара 50 р.».

Пример 6.Найдите отношение стоимости товара (24 р.) к его массе (8 кг): .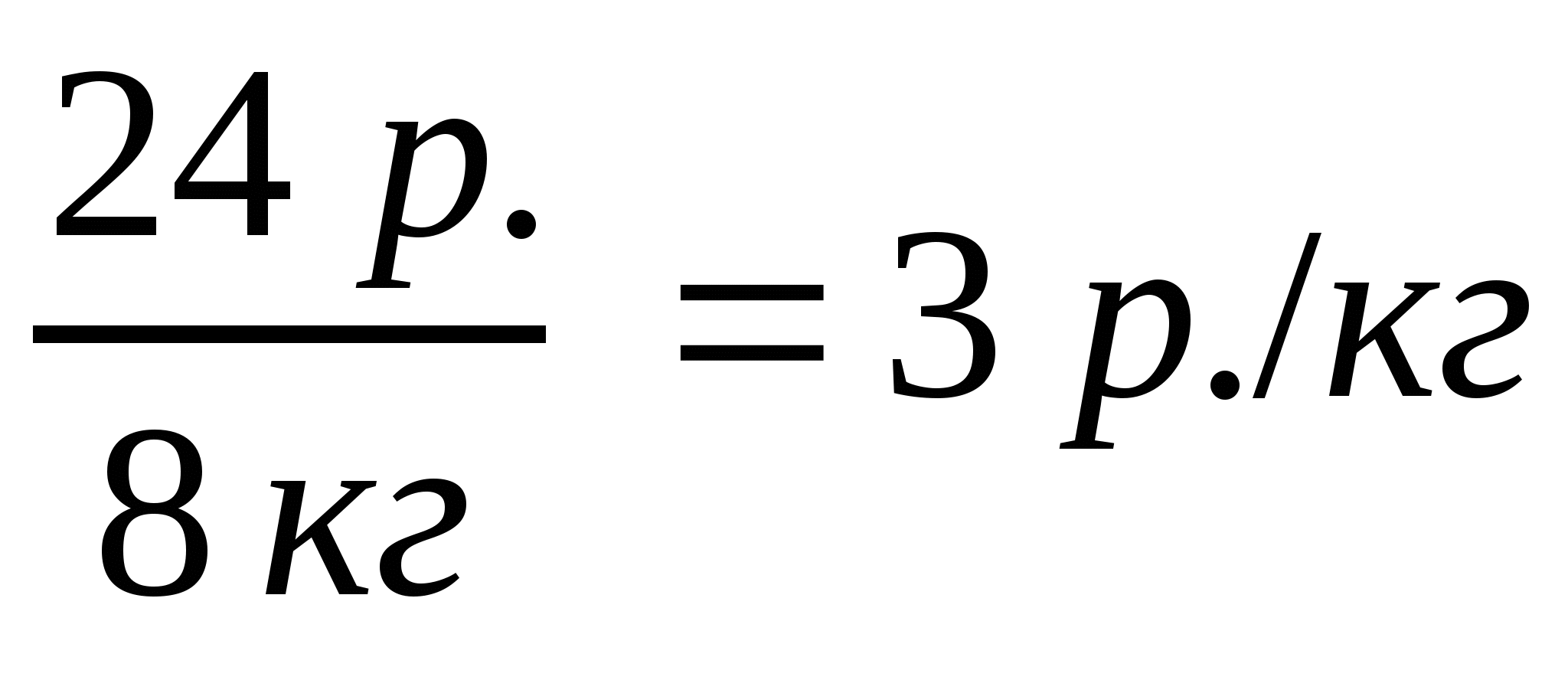

Отношение величин в физике.

Отношение массы тела (кг) к его объему (м³) есть новая величина -плотность вещества, выраженная в единицах плотности (кг/м³).

.

Пример 7. Найдите отношение массы бруса (120 кг) к его объёму (40 м³): .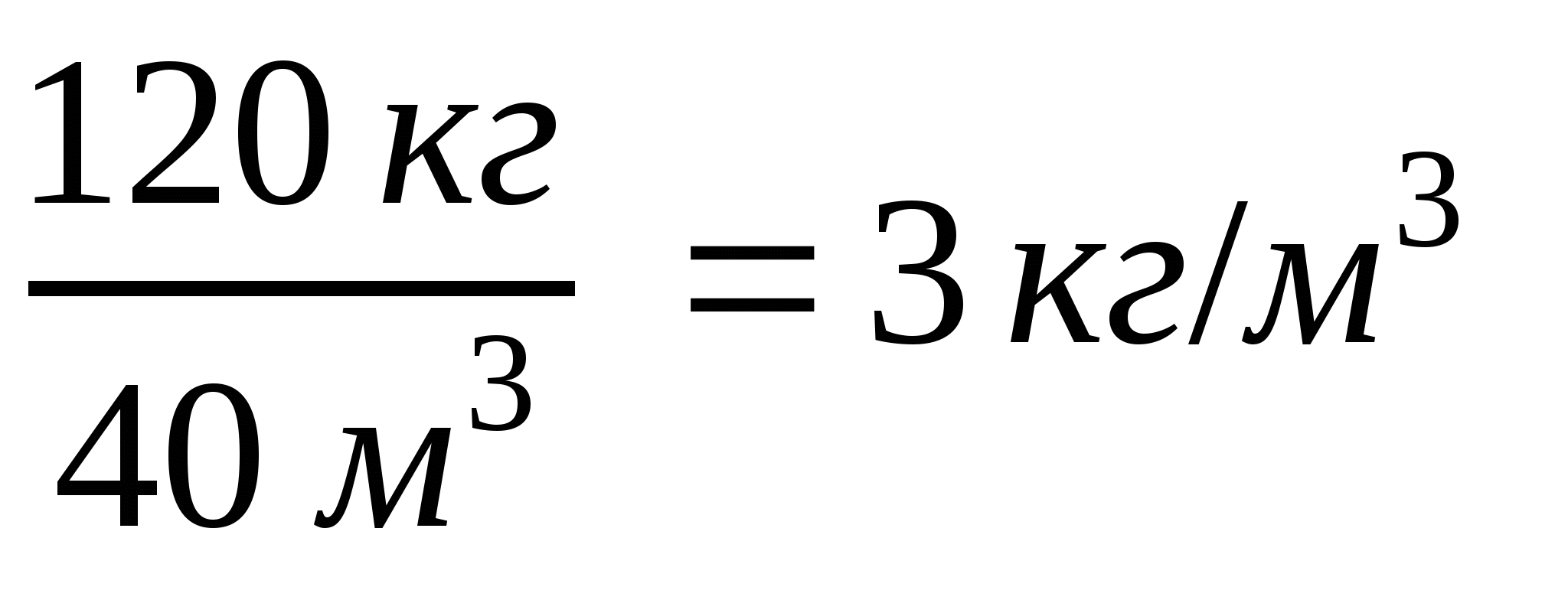

Отношение величин в химии.

Отношение массы вещества (например, соли) (кг) к объему раствора (м³) есть новая величина - концентрация раствора, выраженная в единицах концентрации (кг/м³). .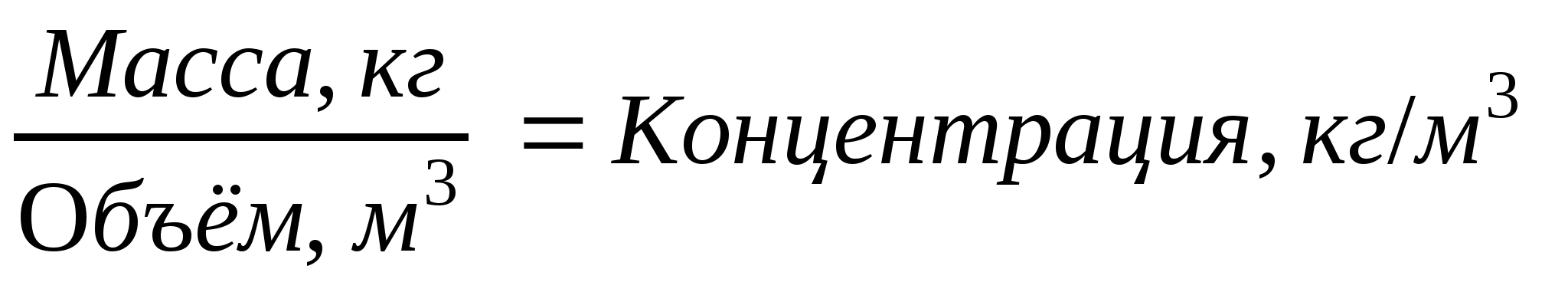

Пример 8. Найдите отношение массы соли (82 кг) к объёму раствора (42 м³): .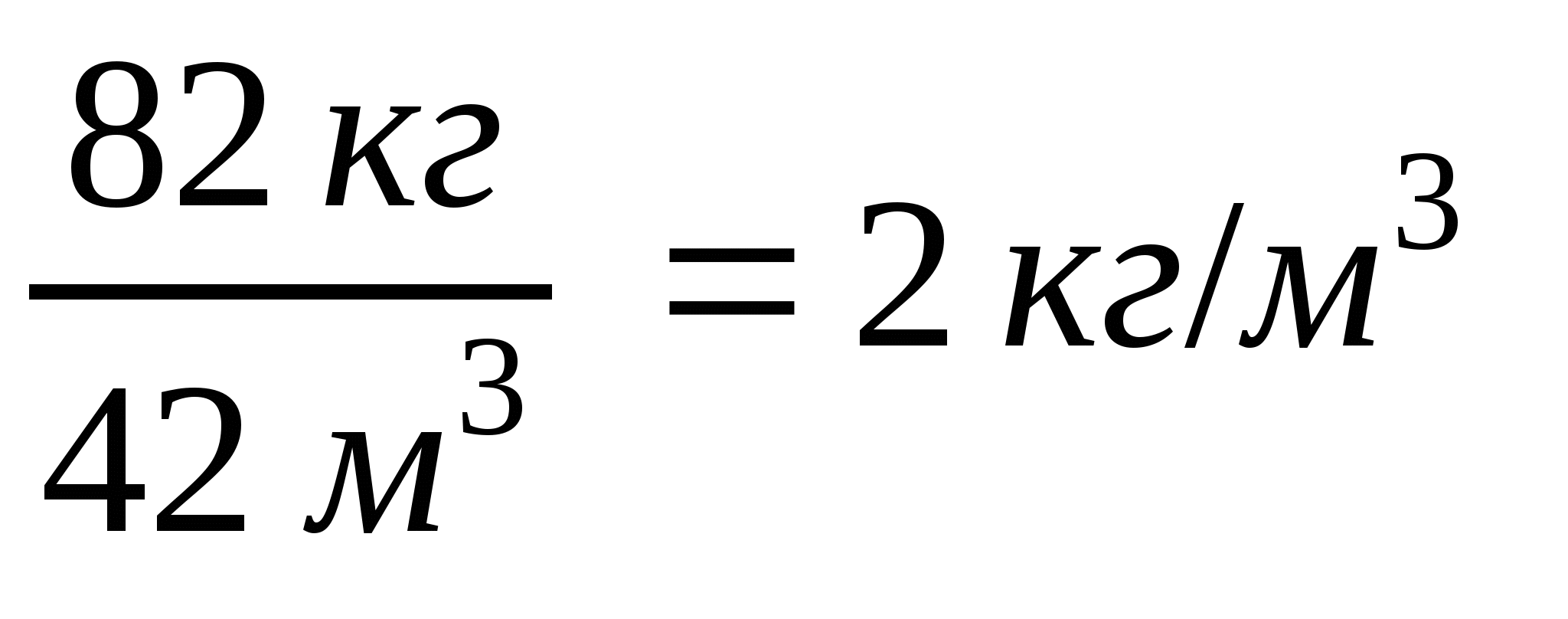

Делают записи.

Выполняют задание

5. Закрепление изученного материала.

Уч.с.7 № 5(а,в). Найдите отношение:

а) , ;

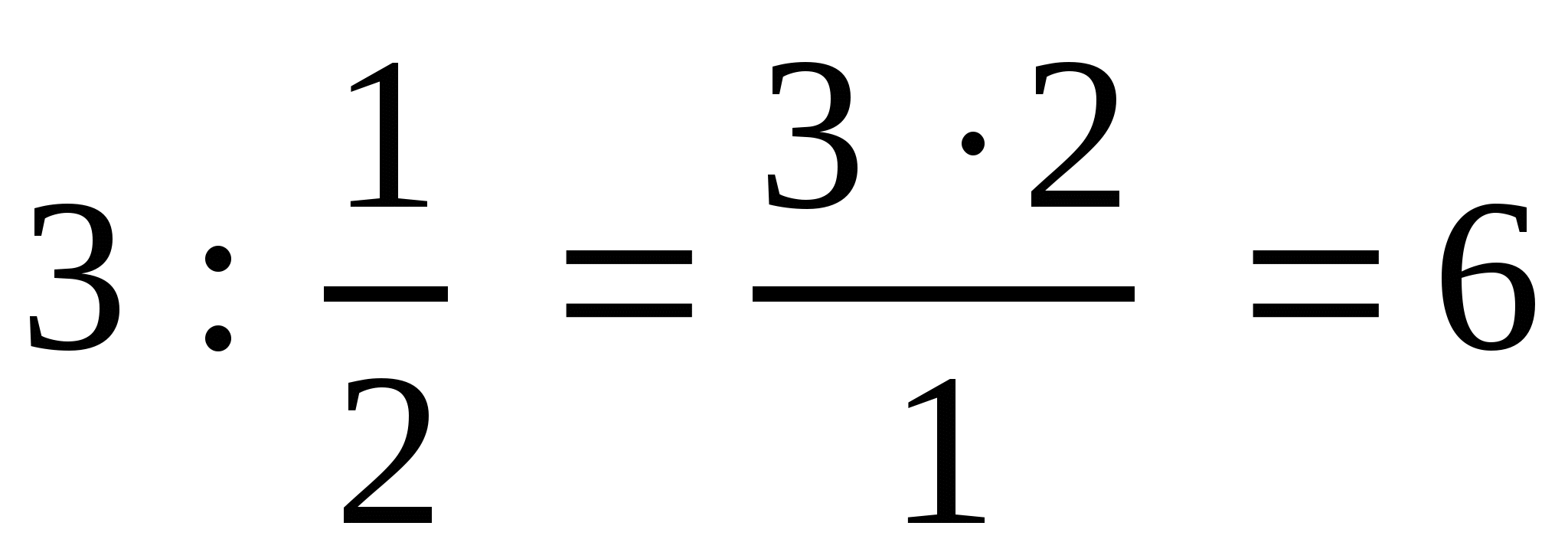в) , .

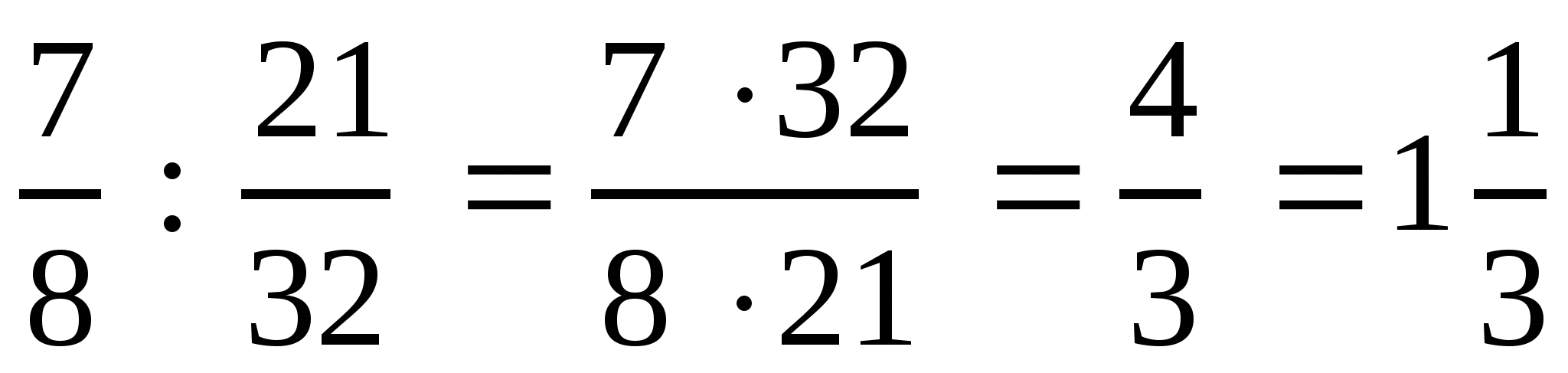Уч.с.7 № 7(а-в). Запишите отношение в виде дроби (там, где можно, упростите отношение):

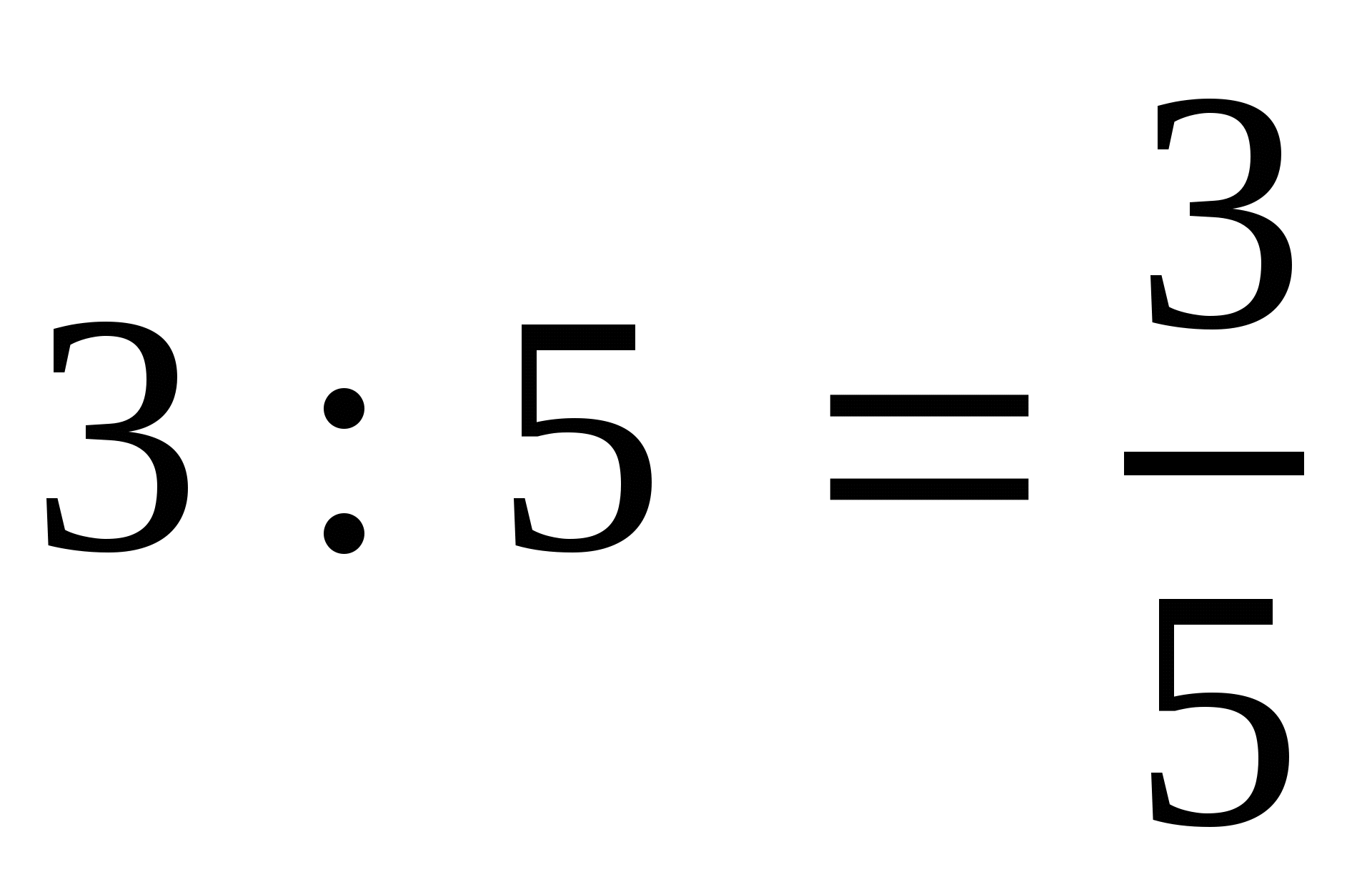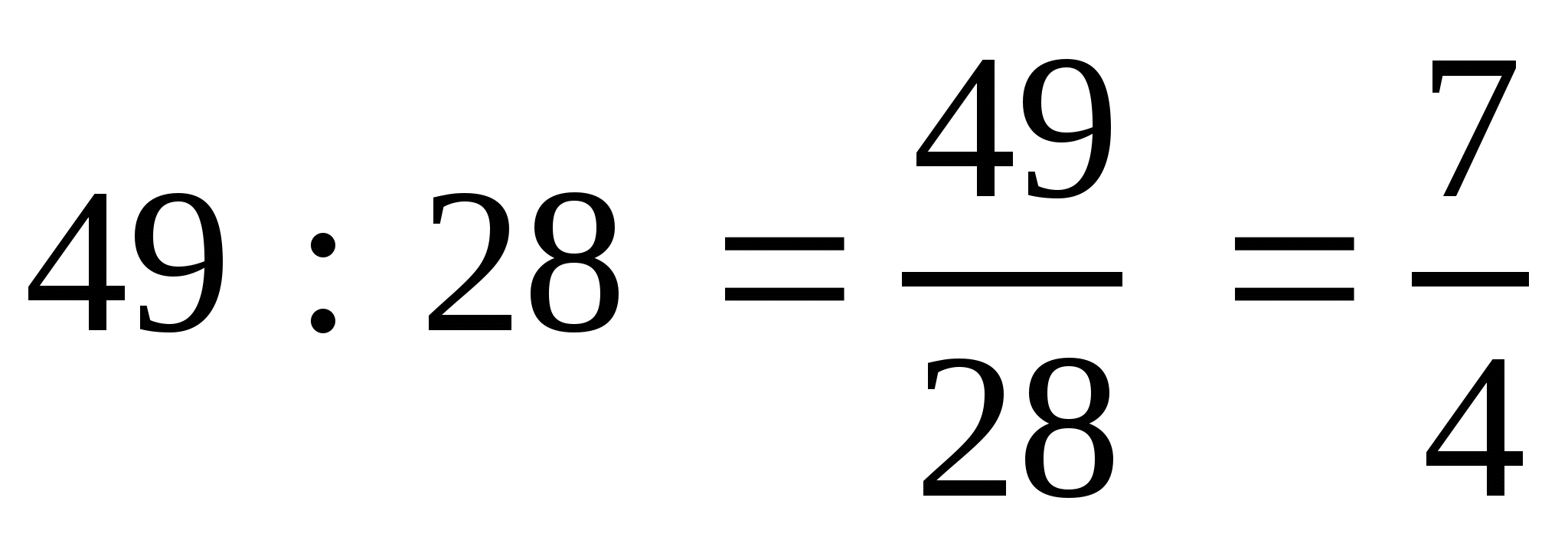а) ; б) ; в) .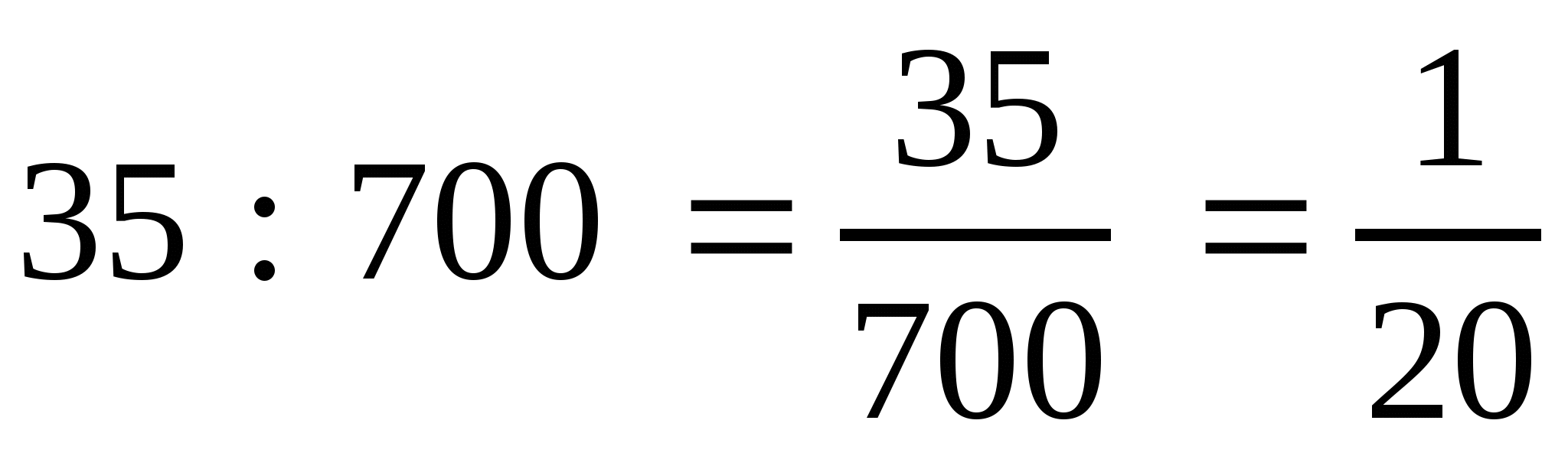

Уч.с.7 № 10(а-в). Упростите отношение величин:

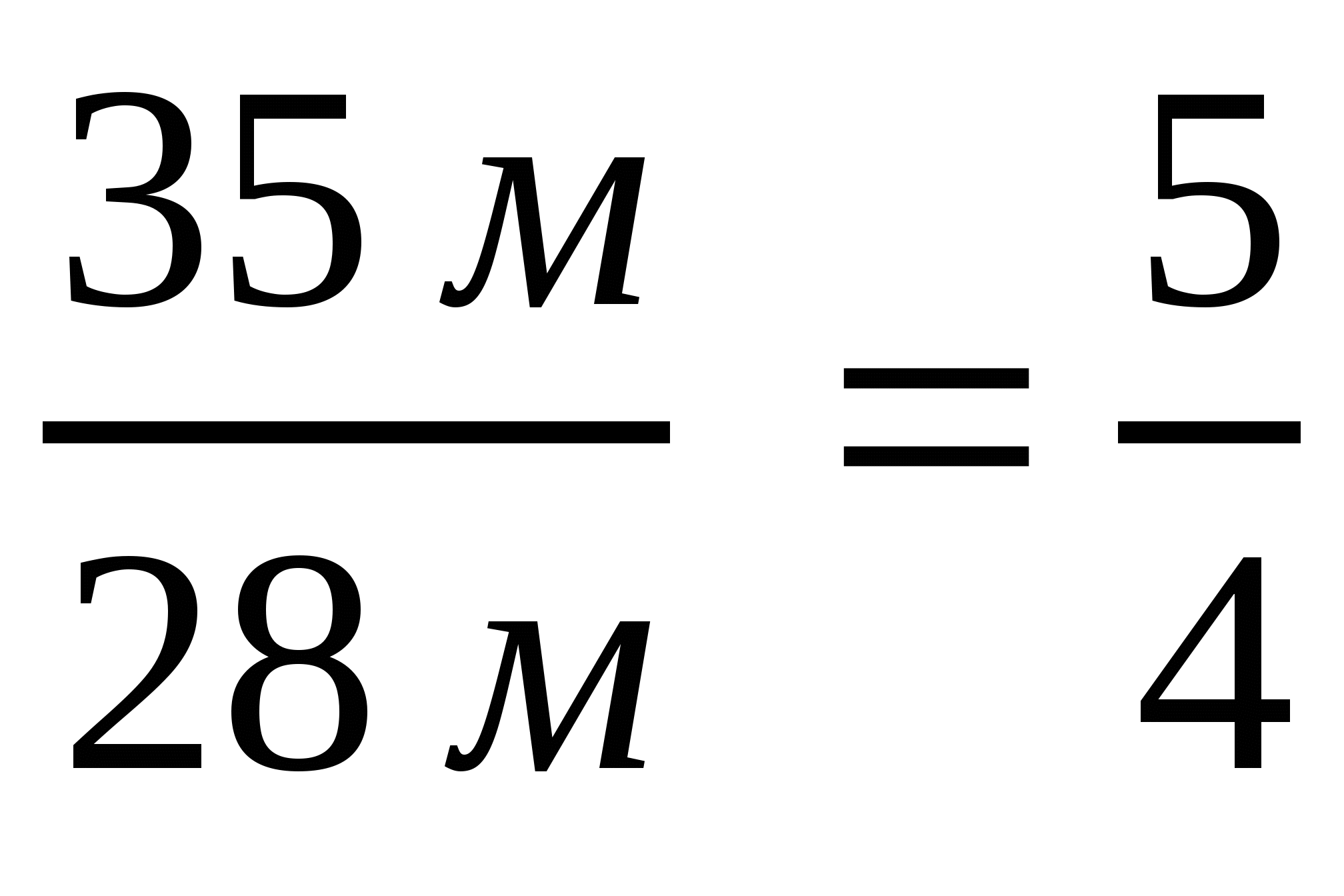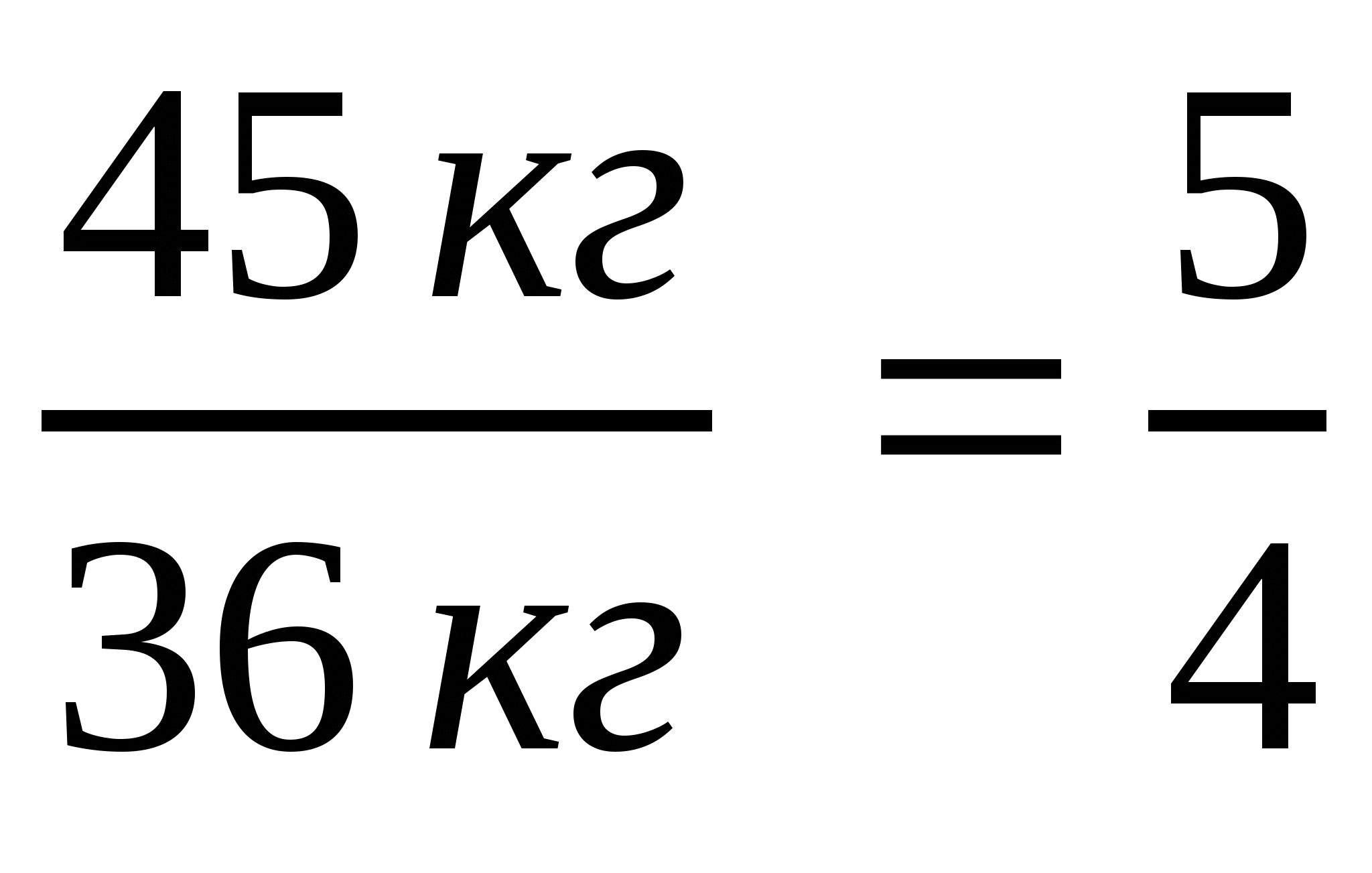а) ; б) ; в) .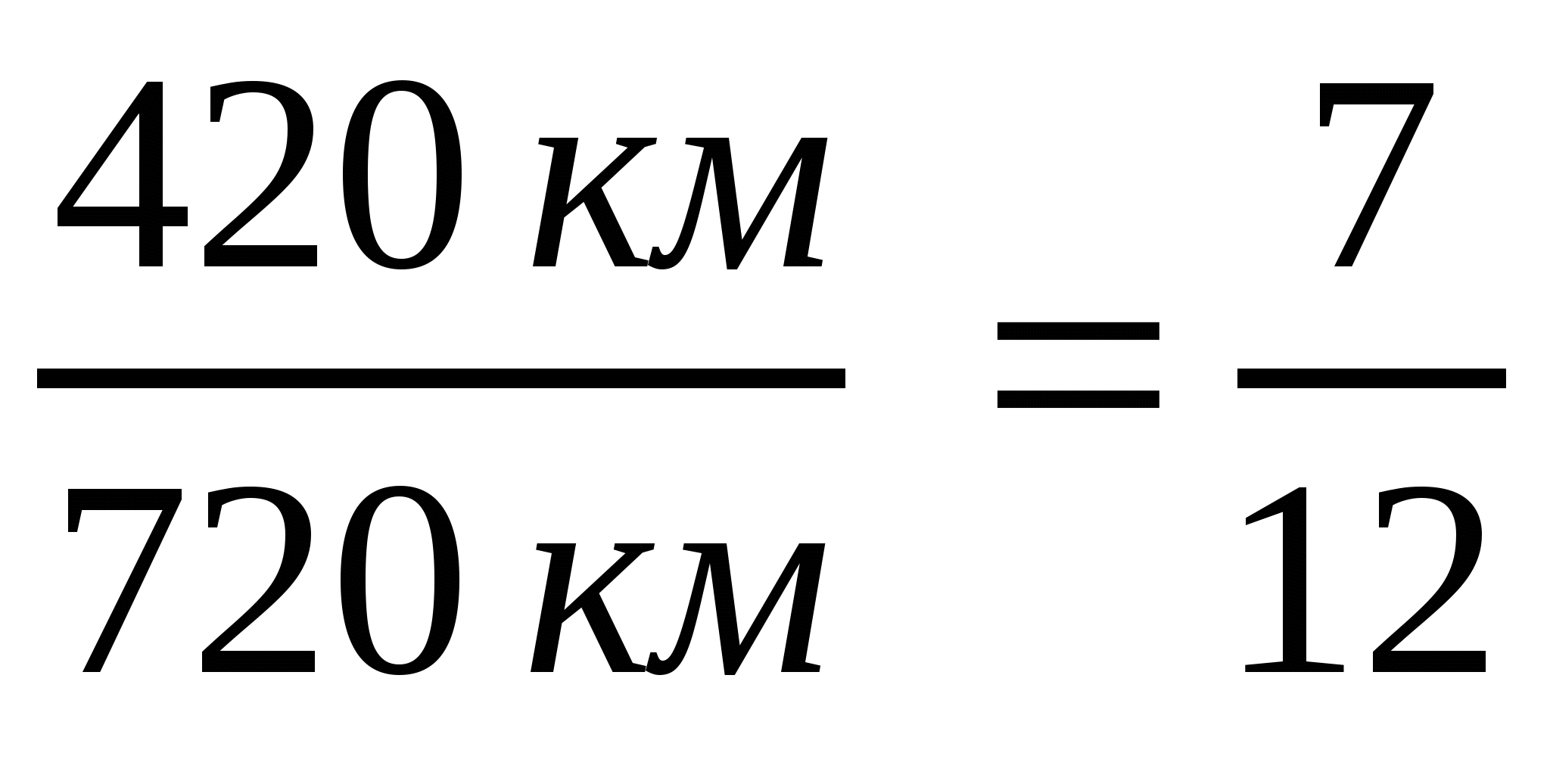

Уч.с.7 № 11(а,б,е). Упростите отношение величин:

а) ;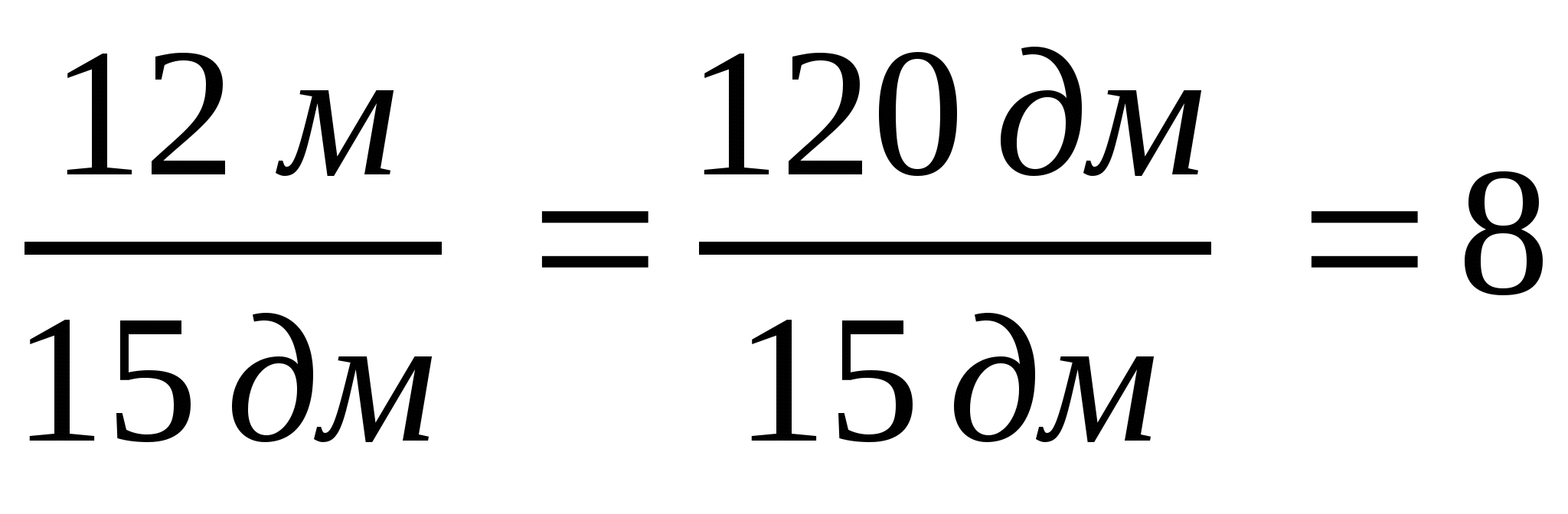

б) ;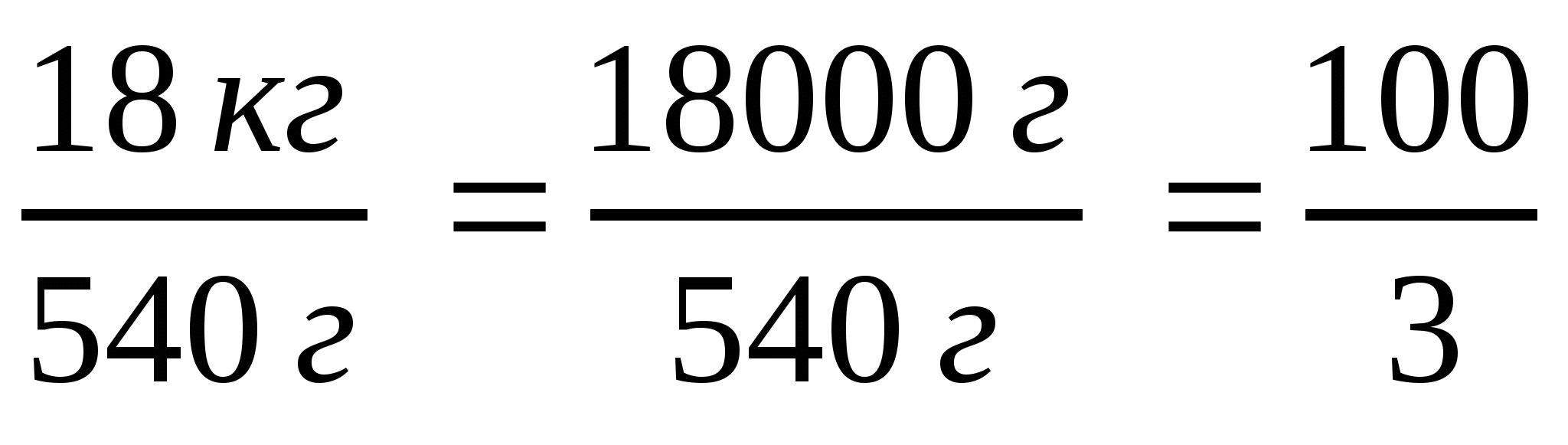

е) .

Уч.с.8 № 13(а). Найдите пройденный путь S, если известны скорость V и время t равномерного движения: а) V = 2 м/с, t = 3 с.

S = V  t,

S = 2  3 = 6 (м). Ответ: 6 м.

Уч.с.8 № 14(а). Найдите скорость равномерного движения V, если известны пройденный путь S и время t: а) S = 6 м, t = 3 с.

,

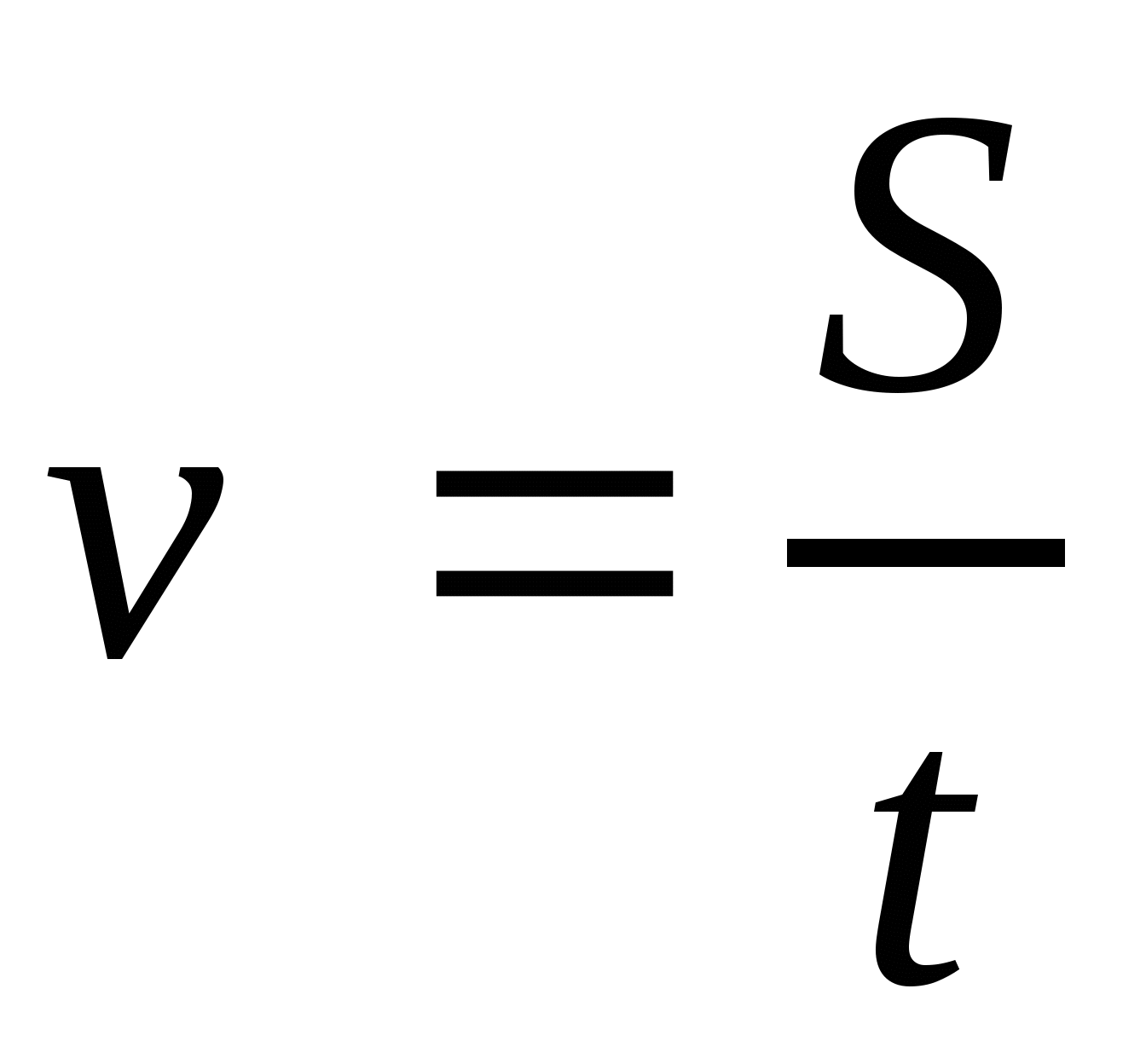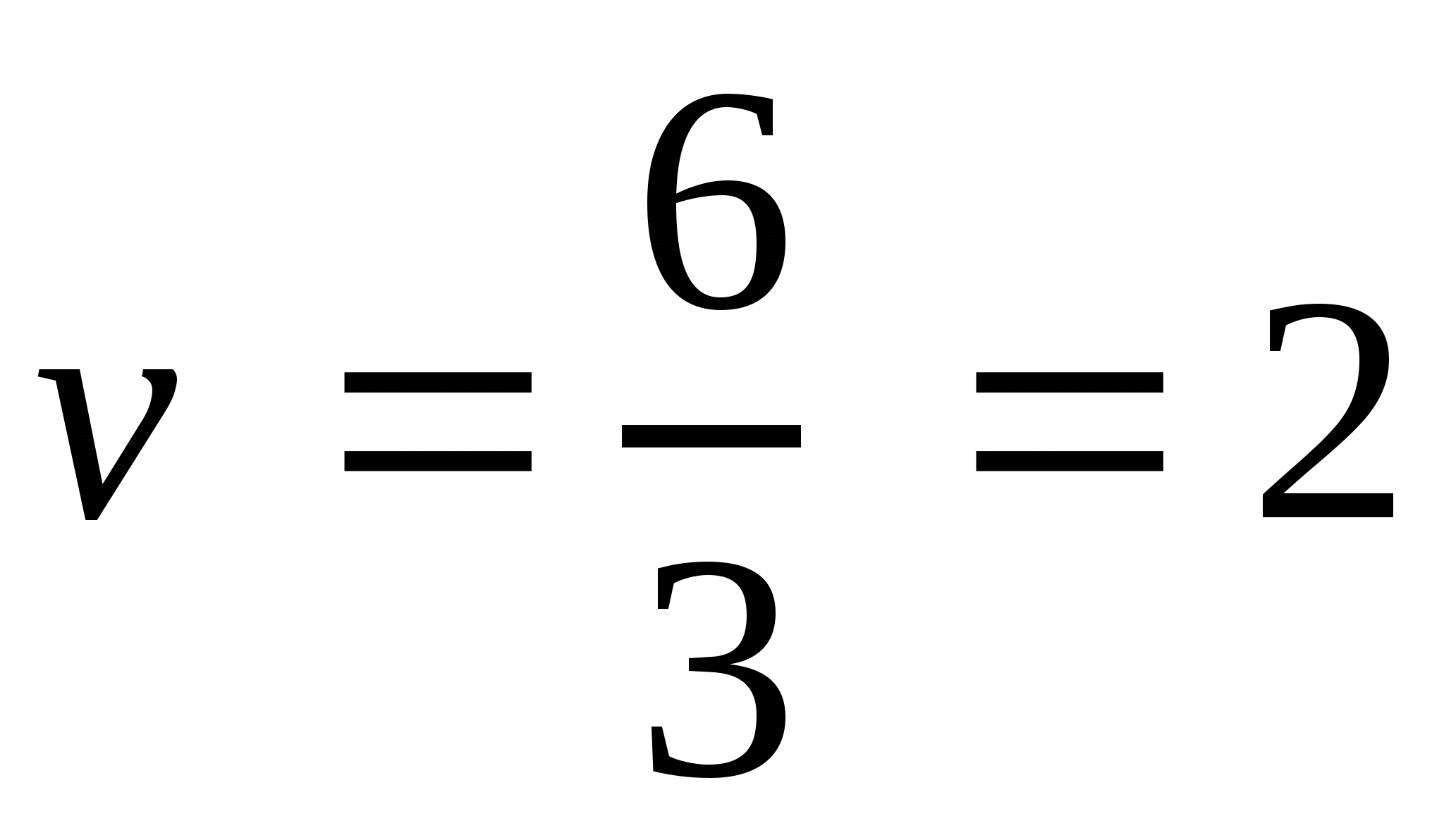(м/с). Ответ: 2 м/с.

Выполняют задание

6. Домашнее задание.

П. 1.1 (выучить теорию). № 5(б,г), 7(г-е), №10(г-е), № 11(в-д), 15(а).

Воспринимают информацию, записывают в дневники домашнее задание

7. Подведение итогов. Рефлексия.

1.​ Продолжите предложения:

Сегодня я узнал…

Было интересно…

Я понял, что…

Теперь я могу…

Я научился…

У меня получилось…

Я попробую….

Меня удивило…

Мне захотелось…

2.​ Оценить отдельных учащихся за устные ответы и работу у доски.

Отвечают на поставленные вопросы.

Проводят самооценку.