- Учителю
- Рабочая программа по алгебре 8 класс
Рабочая программа по алгебре 8 класс
РАБОЧАЯ ПРОГРАММА
ПРЕДМЕТ алгебра
КЛАСС 8
ОБРАЗОВАТЕЛЬНАЯ ОБЛАСТЬ МАТЕМАТИКА
ШМО
УЧЕБНЫЙ ГОД 2014 - 2015
УЧИТЕЛЬ Титова Елена Владимировна
Рассмотрена
на заседании ШМО
протокол №
Утверждена
Директор МБОУ СОШ №7
Колесникова Е. И.
-
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА.
Рабочая программа по алгебре для 8 класса, разработана в соответствии с основными положениями Федерального государственного образовательного стандарта начального общего образования, требованиями Примерной основной образовательной программы начального общего образования, Основной образовательной программы общего образования школы, на основе авторской программы Алимова Ш.А. приказ Министерства образования и науки Российской Федерации от 31.03.2014 № 253 «Об утверждении федеральных перечней учебников, рекомендованных к использованию в образовательном процессе в образовательных учреждений, реализующих образовательные программы общего образования и имеющих государственную аккредитацию на 2009/2010 учебный год»;
НОРМАТИВНЫЕ ДОКУМЕНТЫ,
ОБЕСПЕЧИВАЮЩИЕ РЕАЛИЗАЦИЮ ПРОГРАММЫ
№
Нормативные документы
1
Федеральный компонент государственного стандарта образования. Стандарт основного общего образования по математике.//Вестник образования России.2004. №12
2
Программы для общеобразовательных школ, гимназий, лицеев. Математика «Дрофа», Москва, 2004.
3
Приказ Министерства образования и науки Российской Федерации от 31.03.2014 № 253
4
Закон РФ «Об образовании»
Общая характеристика учебного предмета
Алгебра нацелена на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира. Одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных и др.), для формирования у учащихся представлений о роли математики в развитии цивилизации и культуры.
Элементы логики, комбинаторики, статистики и теории вероятностей становятся обязательным компонентом школьного образования, усиливающим его прикладное и практическое значение. Этот материал необходим, прежде всего, для формирования функциональной грамотности - умений воспринимать и анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчеты. Изучение основ комбинаторики позволит учащемуся осуществлять рассмотрение случаев, перебор и подсчет числа вариантов, в том числе в простейших прикладных задачах.
Таким образом, в ходе освоения содержания курса учащиеся получают возможность:
развить представления о числе и роли вычислений в человеческой практике; сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;
овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;
изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
получить представления о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;
развить логическое мышление и речь - умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.
Цели
Изучение алгебры в 8 классе направлено на достижение следующих целей:
-
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
-
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, способности к преодолению трудностей;
-
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
-
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии.
Место предмета в учебном плане
Согласно учебному плану на изучение алгебры в 8 классе отводится 140 ч из расчета 4 ч в неделю.
Общеучебные умения, навыки и способы деятельности
В ходе преподавания алгебры в 8 классе, работы над формированием у учащихся перечисленных в программе знаний и умений, следует обращать внимание на то, чтобы они овладевали умениями общеучебного характера, разнообразными способами деятельности, приобретали опыт:
планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых алгоритмов;
решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;
исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;
ясного, точного, грамотного изложения своих мыслей в устной и письменной речи, использования различных языков математики (словесного, символического, графического), свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства;
проведения доказательных рассуждений, аргументации, выдвижения гипотез и их обоснования;
поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.
Требования к уровню подготовки ученика 8 класса
В результате изучения алгебры ученик должен
знать/понимать
-
существо понятия математического доказательства; приводить примеры доказательств;
-
существо понятия алгоритма; приводить примеры алгоритмов;
-
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
-
как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
-
как потребности практики привели математическую науку к необходимости расширения понятия числа;
-
вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов.
Арифметика
уметь
-
выполнять устно арифметические действия: сложение и вычитание двузначных чисел и десятичных дробей с двумя знаками, умножение однозначных чисел, арифметические операции с обыкновенными дробями с однозначным знаменателем и числителем;
-
записывать большие и малые числа с использованием целых степеней десятки;
-
выполнять арифметические действия с рациональными числами, сравнивать рациональные и действительные числа; находить в несложных случаях значения степеней с натуральными показателями; находить значения числовых выражений;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
решения несложных практических расчетных задач, в том числе c использованием при необходимости справочных материалов, калькулятора, компьютера;
-
устной прикидки и оценки результата вычислений; проверки результата вычисления, с использованием различных приемов;
-
интерпретации результатов решения задач с учетом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений.
Алгебра
уметь
-
составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;
-
выполнять основные действия со степенями с натуральными показателями, с многочленами; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
-
применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
-
решать квадратные уравнения и рациональные уравнения, сводящиеся к ним;
-
решать линейные и квадратные неравенства с одной переменной и их системы;
-
решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;
-
определять координаты точки плоскости, строить точки с заданными координатами; изображать множество решений линейного неравенства;
-
находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
-
определять свойства функции по ее графику; применять графические представления при решении уравнений, систем;
-
описывать свойства изученных функций, строить их графики;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
выполнения расчетов по формулам, для составления формул, выражающих зависимости между реальными величинами; для нахождения нужной формулы в справочных материалах;
-
моделирования практических ситуаций и исследования построенных моделей с использованием аппарата алгебры;
-
описания зависимостей между физическими величинами соответствующими формулами, при исследовании несложных практических ситуаций;
-
интерпретации графиков реальных зависимостей между величинами.
Элементы логики, комбинаторики, статистики и теории вероятностей
уметь
-
извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы и графики;
-
вычислять средние значения результатов измерений;
-
находить частоту события, используя собственные наблюдения и готовые статистические данные;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
выстраивания аргументации при доказательстве и в диалоге;
-
распознавания логически некорректных рассуждений;
-
записи математических утверждений, доказательств;
-
анализа реальных числовых данных, представленных в виде диаграмм, графиков, таблиц;
-
решения практических задач в повседневной и профессиональной деятельности с использованием действий с числами, процентов, длин, площадей, объемов, времени, скорости;
-
понимания статистических утверждений.
-
СОДЕРЖАНИЕ УЧЕБНОГО ПРЕДМЕТА.
1. Повторение материала 7 класса (5 ч)
Цель - повторение пройденного материала, обобщение и систематизация.
Знать: Свойства арифметических действий; правила раскрытия скобок; правила решения линейных уравнений; свойства степени с натуральным показателем; правила умножения и сложения многочленов, способы разложения многочленов на множители; правила сложения и вычитания алгебраических дробей; способы решения систем уравнений с двумя неизвестными.
Уметь: раскрывать скобки; решать уравнения с одним неизвестным сводящиеся к линейным; записывать числа в стандартном виде; приводить подобные члены, выполнять действия с одночленами и многочленами; раскладывать многочлены на множители; выполнять совместные действия над алгебраическими дробями; решать системы двух уравнений с двумя неизвестными.
2. Неравенства (23 ч)
Положительные и отрицательные числа. Модуль (абсолютная величина) числа. Числовые неравенства и их свойства. Почленное сложение и умножение числовых неравенств. Доказательство числовых и алгебраических неравенств. Неравенство с одной переменной. Решение неравенства. Линейные неравенства с одной переменной и их системы. Примеры решения дробно-линейных неравенств. Применение свойств неравенств в оценке значения выражения.
Знать: Определение положительного и отрицательного чисел; определение рационального числа; свойства чисел; определение большего числа; основные свойства числовых неравенств; теоремы о сложении и умножении неравенств; понятие строгого и не строгого неравенства; определение решения неравенства; алгоритм решения неравенств; определение решения систем неравенств; определение числовых промежутков; алгоритм решения систем неравенств; определение модуля числа; правило решения уравнений с модулем; правило решения неравенств с модулем;
Уметь: Выполнять вычисления, доказывать неравенства, решать уравнения используя свойства числовых неравенств; сравнивать числовые неравенства, доказывать неравенства; применять основные свойства неравенств; доказывать неравенства с применением свойств; доказывать и решать неравенства с применением теорем об умножении и сложении; решать линейные неравенства и показывать на числовой прямой множество их решений; решать системы неравенств; записывать результаты с помощью числовых промежутков; решать простейшие уравнения и неравенства содержащие модуль.
3. Приближенные вычисления (13 ч)
Погрешность приближения. Оценка погрешности. Стандартный вид числа. Простейшие вычисления на микрокалькуляторе.
Знать: определение абсолютной погрешности приближения; правило нахождения оценки погрешности; правило округления чисел; определение относительной погрешности; запись числа в стандартном виде; правило сложения и вычитания, умножения и деления приближенных значений;
Уметь: Находить абсолютную погрешность приближения; находить приближенное значение с недостатком и с избытком; давать оценку абсолютной погрешности; округлять числа; находить относительную погрешность; записывать числа в стандартном виде; выполнять задания с применением правил сложения, вычитания, умножения и деления приближенных значений
4. Квадратные корни (16 ч)
Понятие рациональных, иррациональных чисел. Общие сведения о действительных числах. Квадратный корень, приближенное значение квадратного корня. Свойства квадратных корней. Преобразование выражений, содержащих квадратные корни.
Знать: определения квадратного корня, арифметического квадратного корня,свойства арифметического квадратного корня.
Уметь: выполнять преобразование числовых выражений, содержащих квадратные корни; решать уравнения вида x2=а; находить приближенные значения квадратного корня; находить квадратный корень из произведения, дроби, степени, строить график функции и находить значения этой функции по графику или по формуле; выносить множитель из-под знака корня, вносить множитель под знак корня; выполнять преобразование выражений, содержащих квадратные корни.
5. Квадратные уравнения (30 ч)
Квадратное уравнение. Формулы корней квадратного уравнения. Теорема Виета. Решение рациональных уравнений. Решение задач, сводящихся к квадратным и рациональным уравнениям.
Знать, что такое квадратное уравнение, неполное квадратное уравнение, приведенное квадратное уравнение; формулы дискриминанта и корней квадратного уравнения, терему Виета и обратную ей; какие уравнения называются дробно-рациональными, какие бывают способы решения уравнений, понимать, что уравнение это математический аппарат решения разнообразных задач математики, смежных областей знаний, практики.
Уметь решать квадратные уравнения выделением квадрата двучлена, решать квадратные уравнения по формуле, решать неполные квадратные уравнения, решать квадратные уравнения с помощью теоремы, обратной теореме Виета, использовать теорему Виета для нахождения коэффициентов и свободного члена квадратного уравнения; решать текстовые задачи с помощью квадратных уравнений; решать дробно-рациональные уравнения, решать уравнения графическим способом, решать текстовые задачи с помощью дробно-рациональных уравнений.
6. Квадратичная функция (23 ч)
Понятие функции. Область определения функции. Способы задания функции. График функции, возрастание и убывание функции, наибольшее и наименьшее значения функции, нули функции, промежутки знакопостоянства. Чтение графиков функций. Квадратичная функция, ее график, парабола. Координаты вершины параболы, ось симметрии. Параллельный перенос графиков вдоль осей координат и симметрия относительно осей.
Знать основные свойства функций, уметь находить промежутки знакопостоянства, возрастания, убывания функций
Уметь находить область определения и область значений функции, читать график функции; выполнять разложение квадратного трехчлена на множители; строить график функции у=кх2 , выполнять простейшие преобразования графиков функций; строить график квадратичной функции, выполнять простейшие преобразования графиков функций, находить по графику нули функции, промежутки, где функция принимает положительные и отрицательные значения; решать квадратное уравнение графически; решать неравенство ах2 +вх+с.≥0 на основе свойств квадратичной функции.
7. Квадратные неравенства (18 ч)
Квадратные неравенства. Способы решения квадратных неравенств. Примеры решения дробно-линейных неравенств.
Знать: определение числового неравенства с одной переменной, что называется решением неравенства с одной переменной, что значит решить неравенство, свойства числовых неравенств, понимать формулировку задачи решить неравенство.
Уметь: записывать и читать числовые промежутки, изображать их на числовой прямой, решать линейные неравенства с одной переменной, решать квадратные неравенства; решать системы неравенств с одной переменной.
8. Итоговое повторение (12 ч)
Закрепление знаний, умений и навыков, полученных на уроках по данным темам (курс алгебры 8 класса).
-
СТРУКТУРА КУРСА.
№п/п
Модуль
Примерное
количество
часов
1
Повторение курса алгебры 7 класса
5
2
Неравенства
23
3
Приближенные вычисления
13
4
Квадратные корни
16
5
Квадратные уравнения
30
6
Квадратичная функция
23
7
Квадратные неравенства
18
8
Повторение и решение задач
12
Итого:
140
-
КОНТРОЛЬ РЕАЛИЗАЦИИ ПРОГРАММЫ.
СТАРТОВЫЙ КОНТРОЛЬ.
Вариант 1.
-
Упростите выражение (а + 6)2 - 2а (3 - 2а).
-
Решите систему уравнений: .
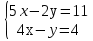
-
а) Постройте график функции у = 2х - 2.
б) Определите, проходит ли график функции через точку А (-10; -20).
-
Разложите на множители:
a) 2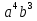 -2
-2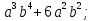 б) х2-3х-3у-у2.
б) х2-3х-3у-у2.
-
Из пунктаАвниз по реке отправился плот. Через 1 ч навстречу ему из пунктаВ, находящегося в 30 км от А, вышла моторная лодка, которая встретилась с плотом через 2 ч после своего выхода. Найдите собственную скорость лодки, если скорость течения реки 2 км/ч.
-
Вариант 2.
-
Упростите выражение (х - 2)2 - (х- 1) (х + 2).
-
Решите систему уравнений: .
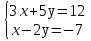
-
а) Постройте график функции у=- 2х+2.
б) Определите, проходит ли график функции через точку А (10; -18).
4. Разложите на множители:
а)
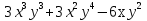 ; б) 2а +
; б) 2а + 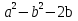 .
. 5. Из поселка на станцию, расстояние между которыми 32 км, выехал велосипедист. Через0,5 ч навстречу ему со станции выехал мотоциклист и встретил велосипедиста через 0,5 ч после своего выезда. Известно, что скорость мотоциклиста на 28 км/ч больше скорости велосипедиста. Найдите скорость каждого из них.
-
ПЕРЕЧЕНЬ ПРОВЕРОЧНЫХ РАБОТ ПО МОДУЛЯМ.
№п/п
Тема
1
Неравенства
2
Приближенные вычисления
3
Квадратные корни
4
Квадратные уравнения
5
Квадратичная функция
6
Квадратные неравенства
7
Итоговая
ИТОГОВЫЙ КОНТРОЛЬ.
Вариант 1.
-
Решить неравенство
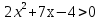 .
. -
Упростить выражение
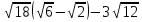 .
. -
Решить систему уравнений :
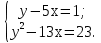
-
Мастер должен был изготовить 72 детали, а ученик 64 детали. Изготовляя в час на 4 детали больше, чем ученик, мастер выполнил заказ на 2 ч раньше. Сколько деталей изготовлял в час мастер и сколько ученик?
-
Найти координаты вершины параболы
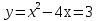 и координаты точек пересечения этой параболы с осями координат.
и координаты точек пересечения этой параболы с осями координат.
Вариант 2.
-
Решить неравенство
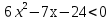 .
. -
Упростить выражение
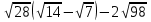 .
. -
Решить систему уравнений :
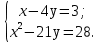
-
Две соревнующиеся бригады рабочих должны были изготовить по 240 деталей. Первая бригада изготовляла в день на 8 деталей больше, чем вторая, и в результате выполнила заказ на 1 день раньше второй. Сколько деталей изготовляла в день каждая бригада?
-
Найти координаты вершины параболы
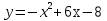 и координаты точек пересечения этой параболы с осями координат.
и координаты точек пересечения этой параболы с осями координат.
КОМПЛЕКТ ТЕОРЕТИЧЕСКИХ ВОПРОСОВ НА КОНЕЦ ГОДА.
1
Определение рационального числа.
2
Сформулируйте свойства чисел
3
Что называется числовым неравенством?
4
Сформулировать свойства числовых неравенств.
5
Дать определение модуля числа.
6
Что такое числовые промежутки?
7
Какие неравенства называются строгими, а какие нет?
8
Что называется решением неравенства?
9
Что значит решить неравенство?
10
Что называется решением системы?
11
Что называется абсолютной погрешностью?
12
Что называется относительной погрешностью?
13
Что такое стандартный вид числа?
14
Что называется арифметическим квадратным корнем числа?
15
Что называется рациональным числом?
16
Что называется иррациональным числом?
17
Дать определение понятия тождество.
18
Сформулировать теорему о корне из произведения.
19
Сформулировать теорему о корне из дроби.
20
Что называется квадратным уравнением?
21
В чем заключается метод выделения полного квадрата?
22
Формулы Виета.
23
Дать определение квадратичной функции.
24
Что такое нули функции?
25
Определение наибольшего и наименьшего значения функции.
26
Сформулировать свойства функции 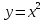
27
Дать определение дать определение квадратному неравенству.
28
В чем заключается метод интервалов?
29
Исследовать квадратичную функцию.
30
Определение интервалов знакопостоянства квадратичной функции.
-
КАЛЕНДАРНО-ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ
4 урока в неделю. Всего 140 за год.
№ п/п
Дата проведения
Наименование разделов, тем и содержание урока
Тип урока или вид учебного занятия
1, 2
2.09 4.09
Повторение курса математики 7 класса
Глава I. Неравенства (23 ч.)
3
5.09
Положительные и отрицательные числа
Изучение нового материала
4
6.09
Положительные и отрицательные числа
Частично-поисковый
5
9.09
Числовые неравенства
Проблемное изложение
6
11.09
Основные свойства числовых неравенств
Проблемное изложение
7
12.09
Основные свойства числовых неравенств
Учебный практикум
8
13.09
Сложение и умножение неравенств
Комбинированный
9
16.09
Диагностическая
контрольная работа
Контроль, оценка и коррекция знаний.
10
18.09
Строгие и нестрогие неравенства
Изучение нового материала
11
19.09
Неравенства с одним неизвестным
Изучение нового материала
12
20.09
Решение неравенств
Учебный практикум
13
23.09
Решение неравенств
Учебный практикум
14
25.09
Решение неравенств
15
26.09
Системы неравенств с одним неизвестным.
Числовые промежутки
Поисковый
16
27.09
Решение систем неравенств
Комбинированный
17
30.09
Решение систем неравенств
Поисковый
18
2.10
Модуль числа. Уравнения и неравенства, содержащие модуль
Комбинированный
19
3.10
Модуль числа. Уравнения и неравенства, содержащие модуль
Поисковый
20-25
4.10; 7.10; 9.10; 10.10; 11.10; 14.10
Решение упражнений к главе I
Обобщение и систематизация знаний
26
16.10
Контрольная работа № 1 по теме: «Неравенства».
Контроль, оценка и коррекция знаний
Глава II. Приближенные вычисления (13)
27
17.10
Приближенные значения величин. Погрешность приближения
Частично-поисковый
28
18.10
Приближенные значения величин. Погрешность приближения
Исследовательский
29
21.10
Оценка погрешности
Изучение нового материала
30
23.10
Оценка погрешности
Решение практических задач
31
24.10
Округление чисел
Частично-поисковый
32
25.10
Относительная погрешность
Изучение нового материала
33
28.10
Контрольная работа за 1 четверть
34
30.10
Простейшие вычисления на микрокалькуляторе
Учебный практикум
35
31.10
Простейшие вычисления на микрокалькуляторе
Учебный практикум
36
1.11
Стандартный вид числа.
Изучение нового материала
37
11.11
Вычисления на микрокалькуляторе.
Учебный практикум
38
13.11
Последовательное выполнение операций на микрокалькуляторе
Учебный практикум
39
14.11
Вычисление на микрокалькуляторе с использованием ячейки памяти
Учебный практикум
40
15.11
Контрольная работа № 2 по теме: «Вычисления на микрокалькуляторе».
Контроль, оценка и коррекция знаний
41
18.11
Вычисление на микрокалькуляторе с использованием ячейки памяти. Работа над ошибками
Учебный практикум
42
20.11
Арифметический квадратный корень
Урок изучения нового материала
43
21.11
Арифметический квадратный корень
Учебный практикум
44
22.11
Действительные числа
Изучение нового материала
45
25.11
Действительные числа
Урок практикум
46
27.11
Квадратный корень из степени
Частично-поисковый
47
28.11
Квадратный корень из степени
Урок практикум
48
29.11
Квадратный корень из степени
Урок проверки знаний и умений
49
2.12
Квадратный корень из произведения
Урок практикум.
50
4.12
Квадратный корень из произведения
Комбинированный
51
5.12
Квадратный корень из дроби
Проблемный урок
52
6.12
Квадратный корень из дроби
Урок практикум
53
9.12
Решение упражнений к главе III
Коррекция знаний и умений по теме
54-57
11.12; 12.12; 13.12; 16.12
Решение упражнений к главе III
Урок подготовки к контр.работе
58
18.12
Административная контрольная работа за 1 полугодие
59
19.12
Решение упражнений к главе III
Урок подготовки к контр.работе
60
20.12
Контрольная работа № 3по теме: «Квадратные корни»
Контроль, оценка и коррекция знаний
61
23.12
Квадратное уравнение и его корни
Работа с книгой (конспект)
62
25.12
Квадратное уравнение и его корни
Отработка навыков решения
63
26.12
Неполные квадратные уравнения. Проверочная работа
Частично-поисковый
64
27.12
Метод выделения полного квадрата
Эвристический урок
65
13.01
Решение квадратных уравнений
Изучение нового материала
66
15.01
Решение квадратных уравнений
Урок практикум
67
16.01
Решение квадратных уравнений
Урок практикум
68
17.01
Решение квадратных уравнений
Частично-поисковый
69
20.01
Приведенное квадратное уравнение. Теорема Виета.
Коррекция знаний и умений по теме
70
22.01
Приведенное квадратное уравнение. Теорема Виета.
Урок подготовки к контр.работе
71
23.01
Уравнения, сводящиеся к квадратным
Частично-поисковый
72
24.01
Уравнения, сводящиеся к квадратным
Опрос по знанию формул
73
27.01
Уравнения, сводящиеся к квадратным
Частично-поисковый
74
29.01
Решение задач с помощью квадратных уравнений
Частично-поисковый
75
30.01
Решение задач с помощью квадратных уравнений
Поисковый
76
31.01
Решение задач с помощью квадратных уравнений
Поисковый
77
3.02
Решение задач с помощью квадратных уравнений
Частично-поисковый
78
5.02
Решение простейших систем, содержащих уравнение второй степени
Частично-поисковый
79
6.02
Решение простейших систем, содержащих уравнение второй степени
Изучение нового материала
80
7.02
Решение простейших систем, содержащих уравнение второй степени
Урок
практикум
81
10.02
Решение упражнений к главе IV
Урок закрепления знаний.
82-89
12.02; 13.02; 14.02; 17.02; 19.02; 20.02; 21.02; 24.02
Решение упражнений к главе IV
Подготовка к контрольной работе.
90
26.02
Контрольная работа № 4 по теме:
« Решение уравнений сводящихся к квадратным».
Контроль, оценка и коррекция знаний
91
27.02
Определение квадратичной функции
Изучение нового материала
92
28.02
Функция у = х2
Изучение нового материала
93
3.03
Функция у = а х2
Частично-поисковый
94
5.03
Функция у = а х2
Урок практикум
95
6.03
Функция у = а х2
Урок практикум
96
7.03
Функция
у = ах2 + bx + с
Изучение нового материала
97
10.03
Функция
у = ах2 +bx + с
Урок практикум
98
12.03
Функция
у = ах2 +bx+ с
Урок практикум
99
13.03
Построение графика квадратичной функции
Частично-поисковый
100
14.03
Построение графика квадратичной функции
Отработка практических навыков
101
17.03
Построение графика квадратичной функции
Отработка практических навыков
102
19.03
Построение графика квадратичной функции
Отработка практических навыков
103-105
20.03; 21.03; 2.04
Построение графика квадратичной функции
практическая работа
106
3.04
Решение упражнений к главе V
Урок закрепления
107-111
4.04; 7.04; 9.04; 10.04; 11.04
Решение упражнений к главе V
Подготовка к контрольной работе.
112
14.04
Контрольная работа № 5 по теме: «Квадратичная функция».
Контроль, оценка и коррекция знаний
Глава VI. Квадратные неравенства (18)
113
16.04
Квадратное неравенство и его решение
Частично-поисковый
114
17.04
Квадратное неравенство и его решение
Урок практикум
115
18.04
Квадратное неравенство и его решение
Комбинированный
116
21.04
Решение квадратного неравенства с помощью графика квадратичной функции
Частично-поисковый
117
23.04
Решение квадратного неравенства с помощью графика квадратичной функции
Проблемное изложение
118
24.04
Решение квадратного неравенства с помощью графика квадратичной функции
Усвоение изученного материала.
119
25.04
Метод интервалов
Урок практикум
120
28.04
Метод интервалов
Урок практикум
121
30.04
Метод интервалов
Комбинированный
122
2.05
Метод интервалов
Комбинированный
123
5.05
Исследование квадратного трехчлена
Частично-поисковый
124-129
7.05; 8.05; 12.05; 14.05; 15.05; 16.05
Решение упражнений к главе VI
Подготовка к контрольной работе.
130
19.05
Контрольная работа № 6 по теме: «Квадратные неравенства».
Контроль, оценка и коррекция знаний
131-137
21.05; 22.05; 23.05; 26.05; 28.05; 29.05; 30.05
Повторение и решение задач (12ч.)
Итоговая контрольная работа
-
ПЛАНИРОВАНИЕ ПО МОДУЛЯМ
Модуль 1
Неравенства
компетенции
Сформировать у учащихся умение решать неравенства первой степени с одним неизвестным и их системы. Знакомство с понятиями уравнений и неравенств, содержащих неизвестное под знаком модуля.
компоненты
Исторические очерки.
УРОВНИ ОСВОЕНИЯ МОДУЛЯ.
ОБЯЗАТЕЛЬНЫЙ МИНИМУМ СОДЕРЖАНИЯ:
-
Положительные и отрицательные числа.
-
Числовые неравенства и их свойства.
-
Сложение и умножение неравенств.
-
Строгие и нестрогие неравенства.
-
Неравенства с одним неизвестным.
-
Системы неравенств с одним неизвестным.
-
Числовые промежутки.
ПОВЫШЕННЫЙ УРОВЕНЬ:
-
Решение текстовых задач, содержащих неравенства.
-
Решение усложнённых неравенств, содержащих неизвестное под знаком модуля.
Модуль 2
Приближенные вычисления
компетенции
Познакомить учащихся с понятием погрешности приближения как показателем точности и качества приближения, выработать умение производить вычисления с помощью калькулятора.
При отсутствии в школе калькуляторов вопросы, связанные с работой на них можно не рассматривать.
компоненты
Исторические очерки.
УРОВНИ ОСВОЕНИЯ МОДУЛЯ.
ОБЯЗАТЕЛЬНЫЙ МИНИМУМ СОДЕРЖАНИЯ:
-
Приближённые значения величин.
-
Погрешность приближения.
-
Относительная погрешность.
-
Простейшие вычисления с калькулятором.
-
Стандартный вид числа.
-
Вычисления на калькуляторе степени числа и числа, обратному данному.
-
Последовательное выполнение нескольких операций на калькуляторе.
-
Вычисления на калькуляторе с использованием ячеек памяти.
ПОВЫШЕННЫЙ УРОВЕНЬ:
-
Вычисления на калькуляторе сложных примеров с использованием ячеек памяти.
Модуль 3
Квадратные корни
компетенции
Систематизировать сведения о рациональных числах; ввести понятия иррационального и действительного чисел; научить выполнять простейшие преобразования выражений, содержащих квадратные корни.
компоненты
Исторические очерки.
УРОВНИ ОСВОЕНИЯ МОДУЛЯ.
ОБЯЗАТЕЛЬНЫЙ МИНИМУМ СОДЕРЖАНИЯ:
-
Понятие квадратного корня.
-
Действительные числа.
-
Квадратный корень из степени, произведения и дроби.
ПОВЫШЕННЫЙ УРОВЕНЬ:
-
Решение примеров, содержащих действия с корнями.
Модуль 4
Квадратные уравнения
компетенции
Выработать умения решать квадратные уравнения, уравнения, сводящиеся к квадратным, и применять их к решению задач.
компоненты
Исторические очерки.
УРОВНИ ОСВОЕНИЯ МОДУЛЯ.
ОБЯЗАТЕЛЬНЫЙ МИНИМУМ СОДЕРЖАНИЯ:
-
Квадратное уравнение и его корни.
-
Неполные квадратные уравнения.
-
Решение квадратных уравнений.
-
Разложение квадратного трёхчлена на множители.
-
Уравнения, сводящиеся к квадратным.
-
Решение задач с помощью квадратных уравнений.
-
Решение простейших систем, содержащих уравнение второй степени.
-
Уравнение окружности.
ПОВЫШЕННЫЙ УРОВЕНЬ:
-
Решение текстовых задач повышенной сложности.
-
Решение квадратных уравнений повышенной сложности.
-
Решение систем повышенной сложности, содержащих уравнение второй степени.
Модуль 5
Квадратичная функция
компетенции
Научить учащихся строить график квадратичной функции.
компоненты
Исторические очерки.
УРОВНИ ОСВОЕНИЯ МОДУЛЯ.
ОБЯЗАТЕЛЬНЫЙ МИНИМУМ СОДЕРЖАНИЯ:
-
Определение квадратичной функции.
-
ФункцияУ=
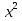 , У=
, У=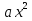 , У=
, У=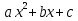 .
. -
Построение графика квадратичной функции.
ПОВЫШЕННЫЙ УРОВЕНЬ:
-
Построение графиков квадратичной функции, содержащих аргумент под знаком модуля.
Модуль 6
Квадратные неравенства
компетенции
Выработать умение решать квадратные неравенства с помощью графика квадратичной функции.
Познакомить учащихся с методом интервалов.
компоненты
Исторические очерки.
УРОВНИ ОСВОЕНИЯ МОДУЛЯ.
ОБЯЗАТЕЛЬНЫЙ МИНИМУМ СОДЕРЖАНИЯ:
-
Квадратное неравенство и его решение.
-
Решение квадратного неравенства с помощью графика квадратичной функции.
ПОВЫШЕННЫЙ УРОВЕНЬ:
1. Решение неравенств повышенной сложности методом интервалов.
-
ИНФОРМАЦИОННО-МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ.
ОСНОВНАЯ ЛИТЕРАТУРА
№
Авторы
Название
Год
издания
Издательство
1
Ш. А. Алимов, Ю. М. Колягин - М
Алгебра учебник для 8 класса общеобразовательных учреждений
2011
Москва
«Просвещение»
2
Ю.М. Колягин, Ю.С. Сидоров и др.
Изучение алгебры 7-9 классах
2006
Издательство «Просвещение»
3
Рурукин А.Н.
Поурочные разработки по алгебре 8 класс
2007
Москва «Вако»
4
Александрова, Л. А.
Алгебра 8 класс: самостоятельные работы для общеобразовательных учреждений.
2007
Москва
«Мнемозина»
5
Мордкович, А. Г.
Алгебра: тесты для 7-9 классов общеобразовательных учреждений.
2007
Москва
«Мнемозина»
6
Дудницын, Ю. П., Е. Е. Тульчинская.
Алгебра. 8 класс: контрольные работы для общеобразовательных учреждений
2007
Москва
«Мнемозина»
7
Арутюнян, Е. Б
Математические диктанты для 5-9 классов .
2000
Москва
«Просвещение»
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА.
№
Авторы
Название
Год издания
Издательство
1
Кузнецова, Л. В.
Сборник заданий для проведения письменного экзамена по алгебре за курс средней школы. 9 класс .
2007
Москва «Дрофа»
2
Клименченко, Д. В.
Задачи по математике для любознательных
2007
Москва
«Просвещение»
3
Д. Пойа
Как решить задачу
1959
«Учпедгиз»
4
Фарков А.В.
Математические кружки в школе.
2006
« Айрис-пресс»
5
Мантуленко, В. Г.
Кроссворды для школьников. Математика
1998
Ярославль «Академия развития»
6
Глейзер Е.И.
История математики в школе.
1982
« Просвещение».