- Учителю
- Разработка урока по теме Решение тригонометрических уравнений
Разработка урока по теме Решение тригонометрических уравнений
Тема: Решение тригонометрических уравнений.(2урока)
Пояснительная записка:
Цели:
-
Образовательные: систематизировать, обобщить, расширить знания и умения учащихся, связанные с применением методов решения тригонометрических уравнений.
-
Развивающие: способствовать формированию умений применять приемы: сравнения, обобщения, выделения главного, переноса знаний в новую ситуацию, развитию математического кругозора, мышления и речи, внимания и памяти.
-
Воспитательные: содействовать воспитанию интереса к математике, активности и мобильности, общей культуры, воспитывать дружеское отношение между учащимися. Эстетическое воспитание осуществляется через формирование умения рационально, аккуратно оформлять задания на доске и в тетради, через наглядные и дидактические пособия.
Тип урока: урок обобщения и систематизации знаний.
Методы обучения: используются репродуктивный метод, с выходом на частично-поисковый (эвристический), решение познавательных обобщающих задач, системные обобщения, самопроверка и проверка уровня знаний.
Формы организации труда: индивидуальная, коллективная, фронтальная.
Оборудование: графо - проектор, плакат «типы уравнений», плакат «формулы», карточки с самостоятельными работами, тетради для самостоятельной работы.
План урока:
-
Оргмомент-2мин
-
Устные упражнения-7мин
-
Самостоятельная робота по вариантам (самопроверка)-8мин
-
Проверка домашнего задания-14мин
-
Классификация тригонометрических уравнений -5мин
-
Решение тригонометрических уравнений-20мин
-
Самостоятельная работа-20мин
-
Домашнее задание-2мин
-
Итог урока-2мин.
Актуальность выбранной темы: данная тема занимает важное место в курсе алгебры и начал анализа, тригонометрические уравнения присутствуют на ЕГЭ как в разделах А,В, так и в разделе С.
Все этапы урока распределены от простого к сложному, логически взаимосвязаны и завершены, определены цели каждого этапа.
На уроке используется наглядность, ТСО, присутствует коллективная, индивидуальная и самостоятельная работа.
Метод решения хорош, если
с самого начала мы можем предвидеть -
и в последствии подтвердить это,- что,
следуя этому методу, мы достигли цели.
Лейбниц.
Ход урока.
1. Оргмомент.
Французский писатель Анатоль Франс однажды заметил: «Учиться можно только весело… Чтобы переваривать знания, надо поглощать их с аппетитом».
Давайте будем следовать этому совету писателя, будем активны, внимательны, все будем делать с довольствием и с большим желанием.
Сегодня урок «Решения тригонометрических уравнений». Повторяем, обобщаем, приводим в систему изученные виды, типы, методы и приемы решения тригонометрических уравнений.
Перед вами задача - показать свои знания и умения по решению тригонометрических уравнений.
2. Устная работа.
Цель: Контроль знаний и приведение в систему знаний по простейшим тригонометрическим уравнениям.
1.Прикаком значении, а имеет решение уравнение sin х=а . cos х=а, tg х=а?
2. По каким формулам решаются эти уравнения?
3. Частные случаи, назовите решение этих уравнений
sin х=0, cos х=1, sin х=-1, sin х=1, cos х=-1, cos х=0.
4. В каком промежутке находится arctg а, arcsin a, arcos a, arcctg a?
5. Чему равен arccos(-a), arcsin(-a), arcctg(-a)?
3. Самостоятельная работа с самопроверкой (ответы записаны на доске с обратной стороны).
Цель: проверить умения и навыки решения простейших тригонометрических уравнений.cos х - 2=0
2cos2х=-![]()
2sin х + 1=0
sin3х =0
3tg4х - ![]() =0
=0
-
sin х+2=0
-
2sin х -
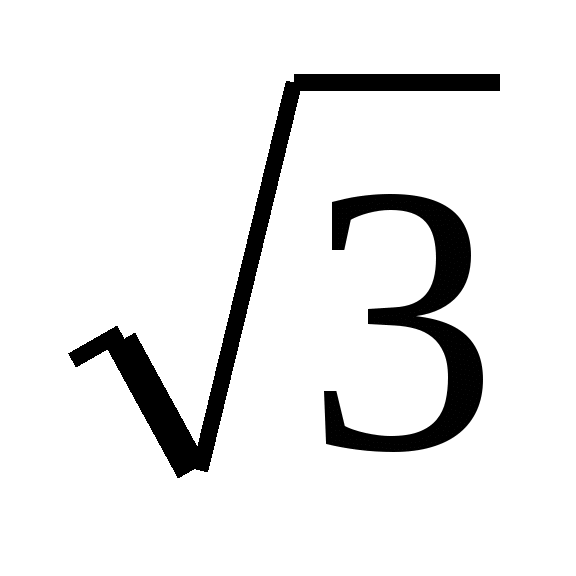 =0
=0
-
cos 3х=1
-
2 cos 2х +
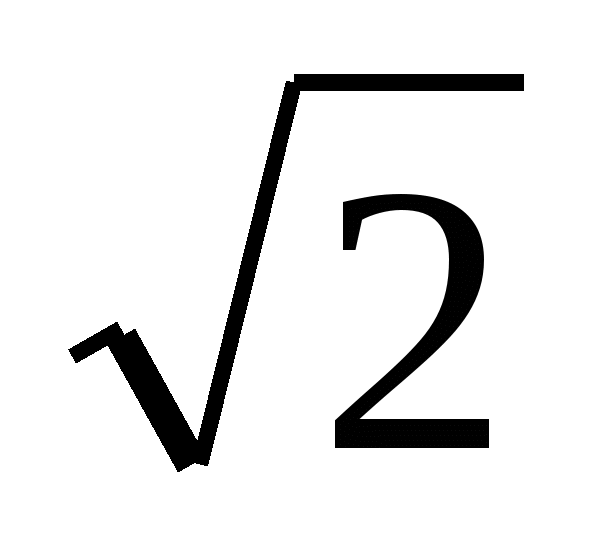 =0
=0
-
tg 3х - 1=0
4. Проверка домашнего задания.
Цель: Ликвидировать пробелы в знаниях, систематизировать умения и навыки решения уравнений различными методами на примере одного уравнения.
Уравнение sin х + cos х = 1 можно решить, по крайне мере, шестью способами. Шесть ребят показывают решения этого уравнения через графо - проектор (каждому учащемуся розданы листочки с решением этого уравнения разными способами).
Проводим сравнительный анализ и комментарий решений.
Способ 1. Сведение к однородному уравнению.
- Выразим sin х, cos х и 1 через функции половинного аргумента:
2sin![]() cos
cos![]() +
cos2
+
cos2 ![]() -
sin2
-
sin2 ![]() =
sin2
=
sin2 ![]() +
cos 2
+
cos 2 ![]()
2sin ![]() cos
cos
![]() -
2sin2
-
2sin2 ![]() =0 / : 2cos2
=0 / : 2cos2 ![]()
tg ![]() -
tg2
-
tg2 ![]() =
0
=
0
tg ![]() (1
- tg
(1
- tg![]() ) =
0
) =
0
Если tg ![]() =
0, то
=
0, то ![]() =
=
![]() п,
п
п,
п![]() z,
х=2
z,
х=2![]() п,
п
п,
п![]() z .
z .
Если ![]() =
1, то
=
1, то ![]() =
=
![]() +
+
![]() к,
к
к,
к![]() z;
х=
z;
х=![]() +
+
![]() к,
к
к,
к![]() z.
z.
Ответ: х=2![]() п,
п
п,
п![]() z
,х=
z
,х=![]() +
2
+
2![]() к,
к
к,
к![]() z.
z.
Способ 2. Преобразование суммы в произведение.
- Выразим cos х через sin(![]() -
х). Получим sin х + sin (
-
х). Получим sin х + sin (![]() -
х) =1
-
х) =1
2 sin 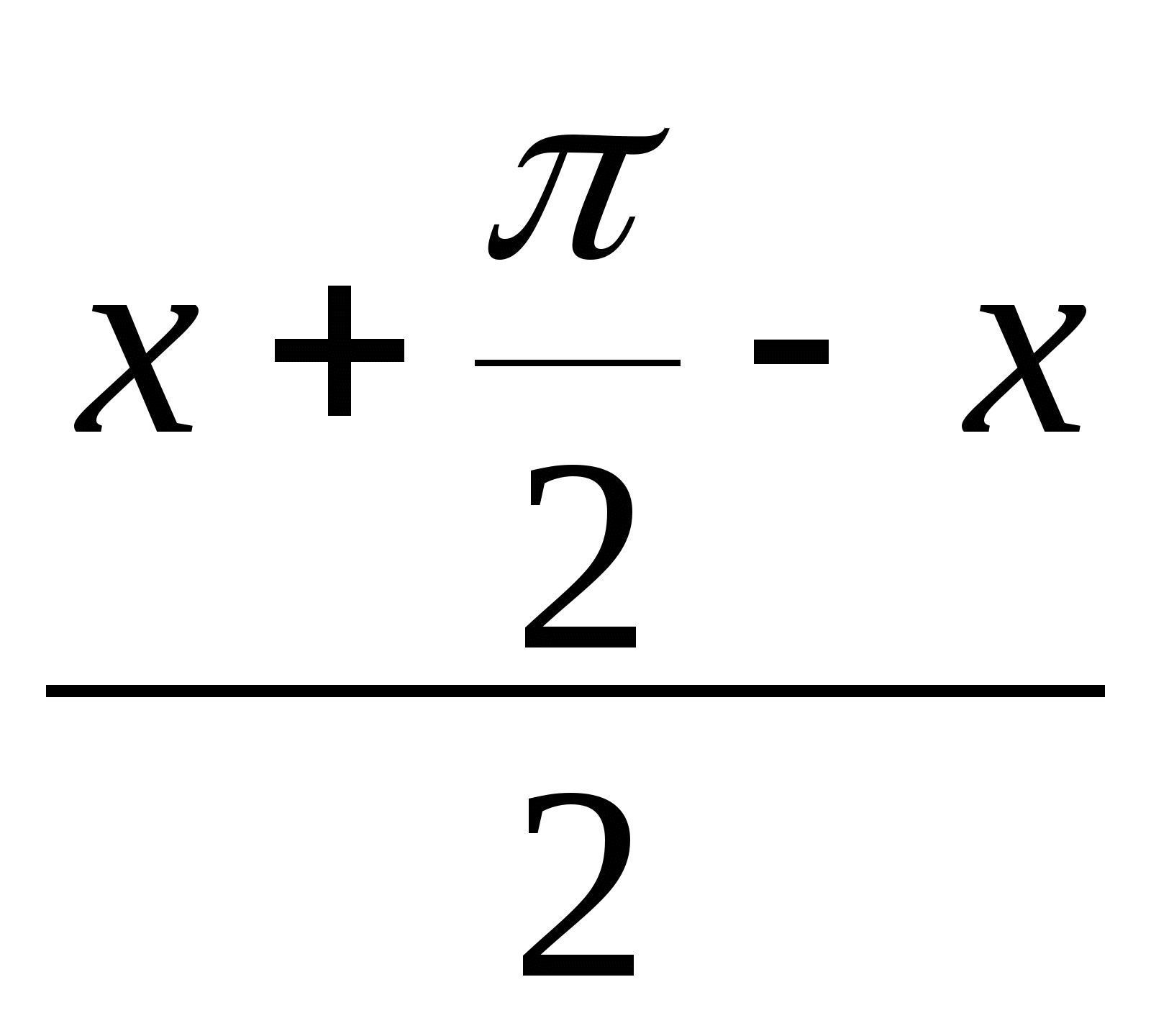 .cos
.cos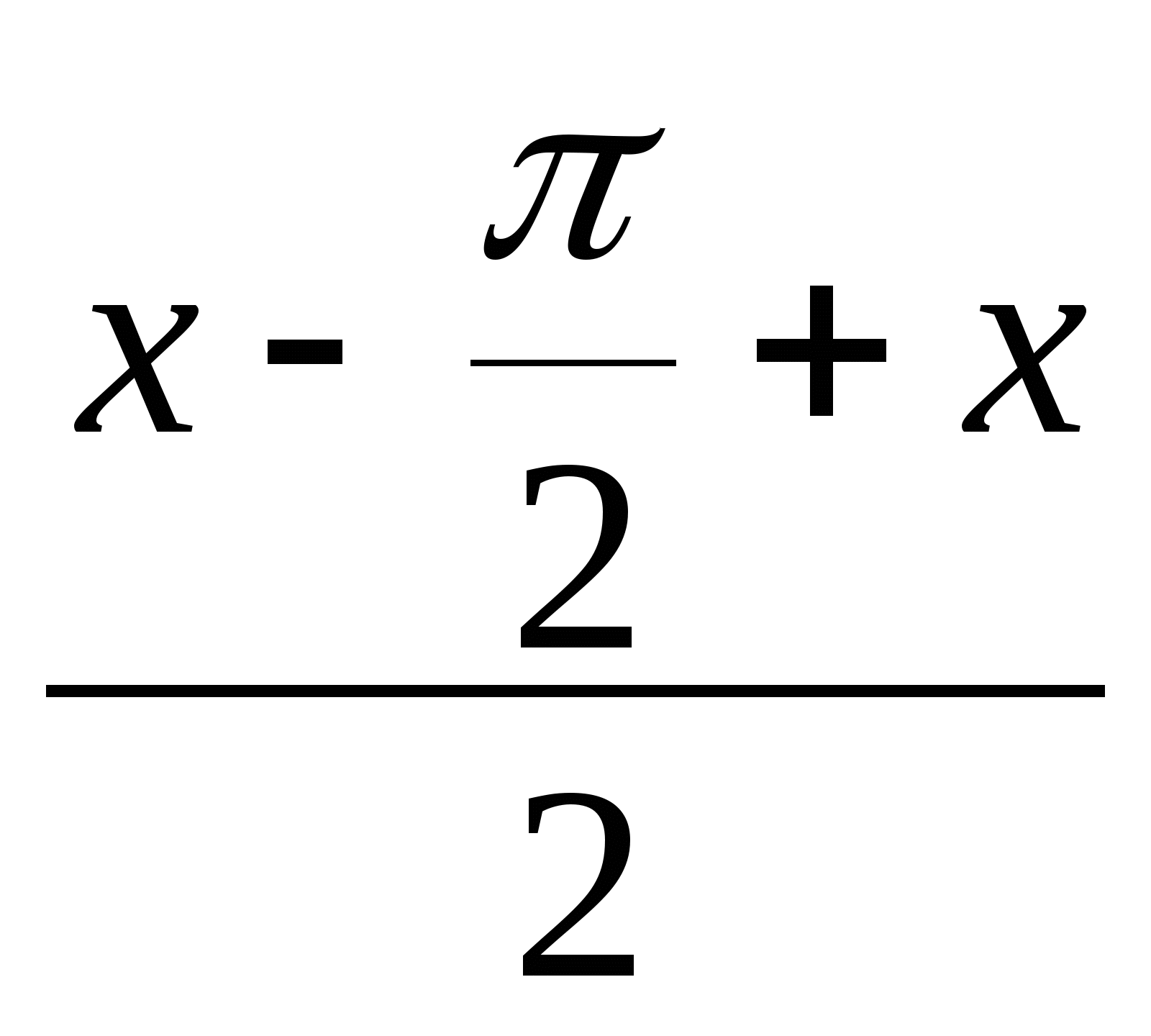 =1,
2sin
=1,
2sin ![]() .cos(х
-
.cos(х
- ![]() )
=1,
)
=1,
![]() cos
(х -
cos
(х - ![]() )
=1, cos(х -
)
=1, cos(х - ![]() )
=
)
=![]() ,
,
![]()
х - ![]() =
arccos
=
arccos![]() +
2
+
2![]() п,
п
п,
п![]() z,
х -
z,
х - ![]() =
- arccos
=
- arccos![]() +
2
+
2![]() к,
к
к,
к![]() z,
z,
х =![]() +
2
+
2![]() п,
п
п,
п![]() z,
х = 2
z,
х = 2![]() к,
к
к,
к![]() z.
z.
Ответ: х =![]() +
2
+
2![]() п,
п
п,
п![]() z,
х = 2
z,
х = 2![]() к,
к
к,
к![]() z.
z.
Способ 3. Введение вспомогательного угла.
- Разделим обе части уравнения ![]() =
=![]()
sin х + cos х =1/ ![]()
![]()
![]() sin
х + cos х
sin
х + cos х![]() =
=
![]()
cos ![]() sin
х + sin
sin
х + sin ![]() cos
х=
cos
х= ![]() ,
sin(х +
,
sin(х + ![]() )
=
)
=![]() ,
,
х + ![]() =(
-1)п arssin
=(
-1)п arssin![]() +
+
![]() п,
п
п,
п![]() z,
z,
х = -![]() +
(-1)
+
(-1)![]() +
+
![]() п,
п
п,
п![]() z .
z .
Ответ: х = -![]() +
(-1)
+
(-1)![]() +
+
![]() п,
п
п,
п![]() z .
z .
Способ 4. С помощью универсальной тригонометрической подстановки.
Sin х = 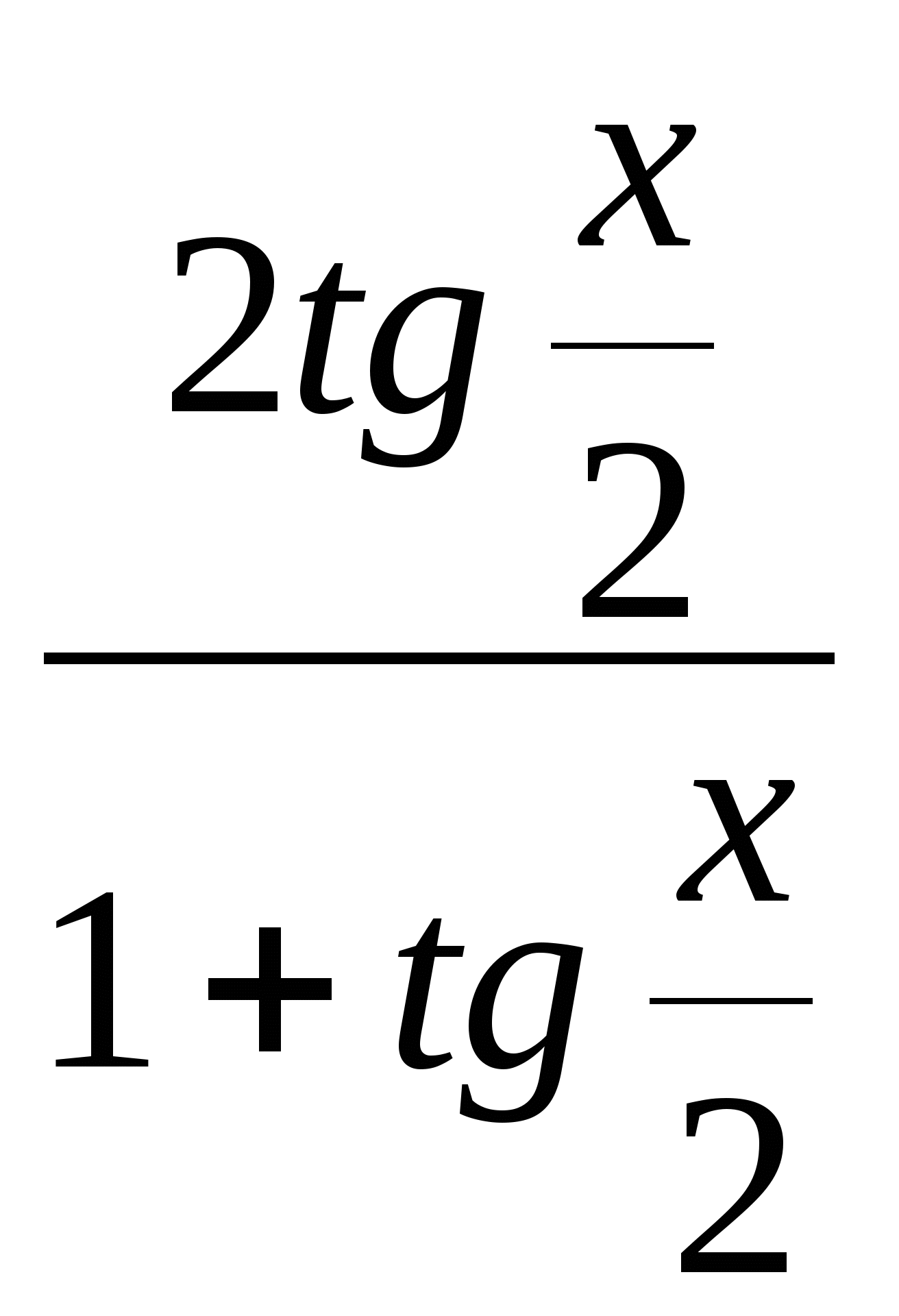 ,
cos х =
,
cos х =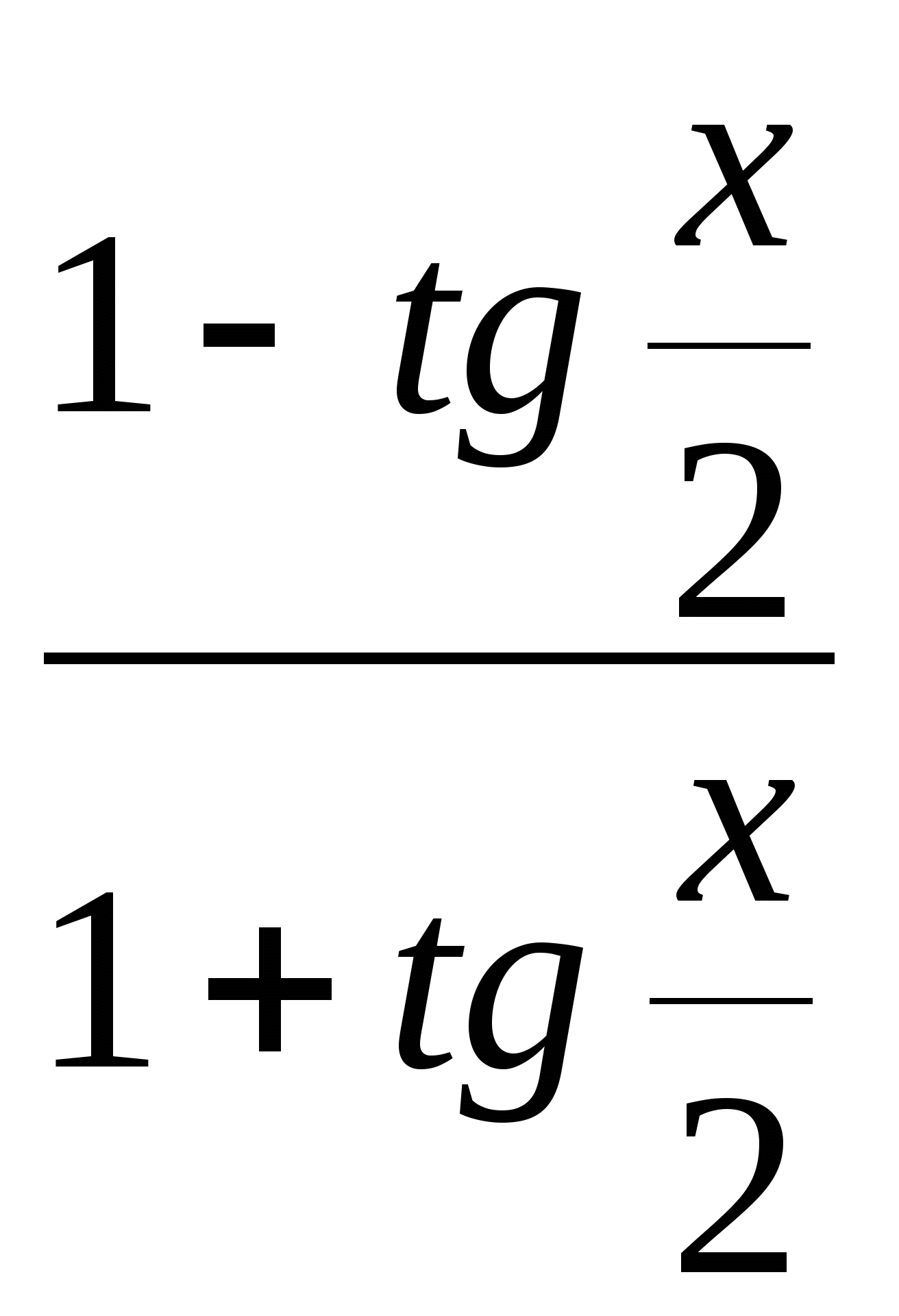 ,
cos
,
cos![]()
![]() 0,
т.е. х
0,
т.е. х![]()
![]() +
2
+
2![]() п,
п
п,
п![]() z
z
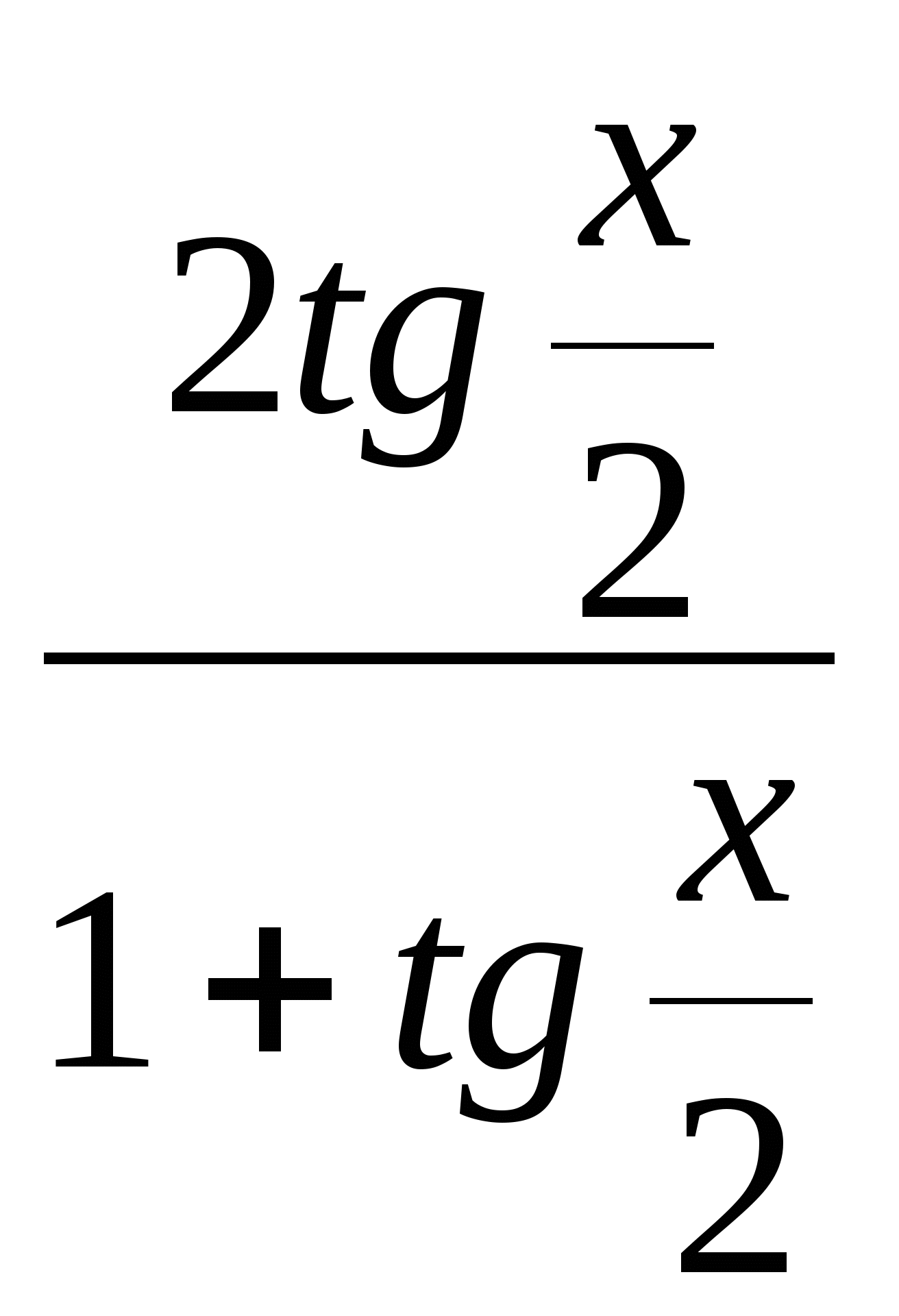 +
+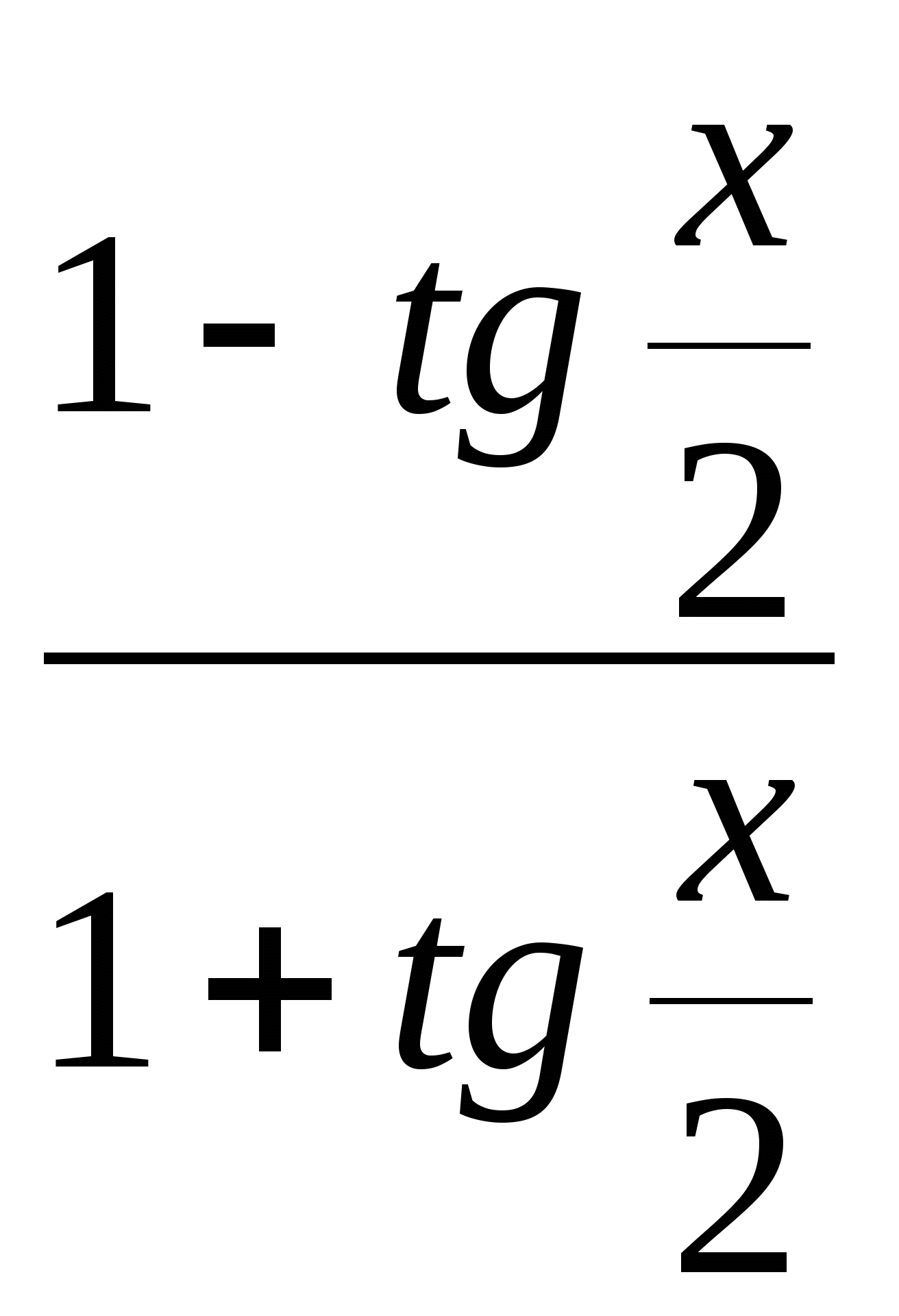 =1, 2tg
=1, 2tg![]() + 1
- tg2
+ 1
- tg2 ![]() =1
+ tg2
=1
+ tg2 ![]() ,
, 2tg
,
, 2tg![]() -
2tg2
-
2tg2 ![]() -0,
-0,
tg![]() (1
- tg
(1
- tg![]() )
=0, tg
)
=0, tg![]() =0
или tg
=0
или tg![]() =
1.
=
1.
Если tg![]() =0,
то х= 2
=0,
то х= 2![]() п,
п
п,
п ![]() z.
z.
Если tg![]() =
1, то х=
=
1, то х=![]() +
2
+
2![]() к,
к
к,
к![]() z.
z.
Ответ: х=2![]() п,
п
п,
п![]() z
,х=
z
,х=![]() +
2
+
2![]() к,
к
к,
к![]() z.
z.
Способ 5. Замена cos х выражением![]()
![]() :
:
![]()
![]() = 1
- sin х
= 1
- sin х
1 - sin2 х = (1 - sin х)2
(1 - sin х)( 1 + sin х) - (1 - sin х)2 = 0
(1 - sin х)( )( 1 + sin х- 1 + sin х) =0
2(1 - sin х) sin х =0
sin х =1 или sin х=0
Если sin х =1, то х =![]() +
2
+
2![]() п,
п
п,
п![]() z.
z.
Если sin х=0 , то х = 2![]() к,
к
к,
к![]() z.
z.
Ответ: х =![]() +
2
+
2![]() п,
п
п,
п![]() z,
х = 2
z,
х = 2![]() к,
к
к,
к![]() z.
z.
Способ 6. Применение формулы sin х + cos х =
![]() sin
(х+
sin
(х+![]() )
)
Исходное уравнение примет вид: ![]() sin
(х+
sin
(х+![]() )
=1 /:
)
=1 /:![]()
sin (х+![]() )
=
)
= ![]() ,
,
х + ![]() =
(-1)пarcsin
=
(-1)пarcsin![]() +
+
![]() п,
п
п,
п![]() z.
z.
х = -![]() +
(-1)
+
(-1)![]() +
+
![]() п,
п
п,
п![]() z .
z .
Ответ: х = -![]() +
(-1)
+
(-1)![]() +
+
![]() п,
п
п,
п![]() z .
z .
- Можно добавить 7 способ. Это графическое решение уравнения.
Как решить графически уравнение?
(В одной системе координат построить графики функций:
а) ![]() или
или ![]() ).
).
Выполните это задание дома.
5.Классификация тригонометрических уравнений.
Цель: привести в систему знания по темам и методам решения тригонометрических уравнений.
Плакат «типы уравнений»
-
Простейшие уравнения и уравнения сводящиеся к ним.
-
Уравнения, сводящиеся к квадратным уравнениям.
-
Способ разложения на множители.
-
Однородные уравнения
(a sin х + b cos х =0 a sin2 х + b cos х sin х + c sin2 х =0)
5. Решение уравнений введением вспомогательного аргумента
(a sin х + b cos х =с ![]()
![]() sin
х +
sin
х + ![]() cos
х =
cos
х = ![]() )
)
6. Способ понижения степени.
7. Решение уравнений преобразованием суммы (разности) тригонометрических функций в произведение.
8. Решение уравнений с помощью преобразования произведения тригонометрических функций в сумму.
9.Уравнения, при решении которых используется универсальная тригонометрическая подстановка.
6.Решение тригонометрических уравнений.
Цель: решение уравнений с указанием четкого алгоритма решения уравнений данного типа.
1)1 - 3sin х cos х - 5cos2х =0
алгоритм:
-
приведение к однородному уравнению.
-
деление левой и правой части на cos2х при условии cos х
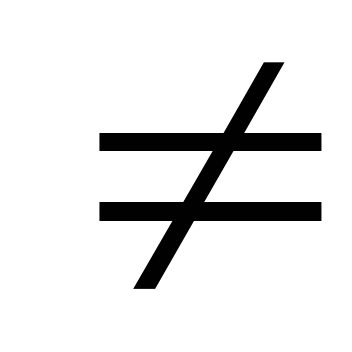 0
0
-
решение квадратного уравнения.
-
подстановка и решение простейших тригонометрических уравнений.
Ответ: х = arctg4 + ![]() п,
п
п,
п![]() z,
х= -
z,
х= - ![]() +
+
![]() к,
к
к,
к![]() z.
z.
2) sin5х + sinх =![]() sin3х
sin3х
алгоритм:
1.формулы преобразования суммы тригонометрических функций в произведение.
2.разложение на множители
3. решение простейших уравнений.
Ответ: х = ![]() ,
к
,
к![]() z,
х =
z,
х = ![]()
![]() +
+
![]() п,
п
п,
п![]() z.
z.
3) sin2 (![]() -
-
![]() ) +
cos2 (
) +
cos2 (![]() +
+![]() ) =
) =
![]()
алгоритм:
-
способ понижения степени
-
выразить квадрат синуса и косинуса половинного угла через косинус угла.
-
решение простейшего уравнения.
Ответ: х = (-1)п![]() +
+
![]() п,
п
п,
п![]() z.
z.
4)sin4х cos 2х = sin2х cos4х
алгоритм:
1.выражение стоящие в правой части перенести на лево
2.примененить формулу синус разности
3.решение простейшего уравнения.
Ответ: х = ![]() ,
п
,
п![]() z.
z.
5) 1 - cos х = 2sin ![]()
алгоритм:
-
сведение к квадратному уравнению
-
применить формулу cos х = 1 - 2sin2
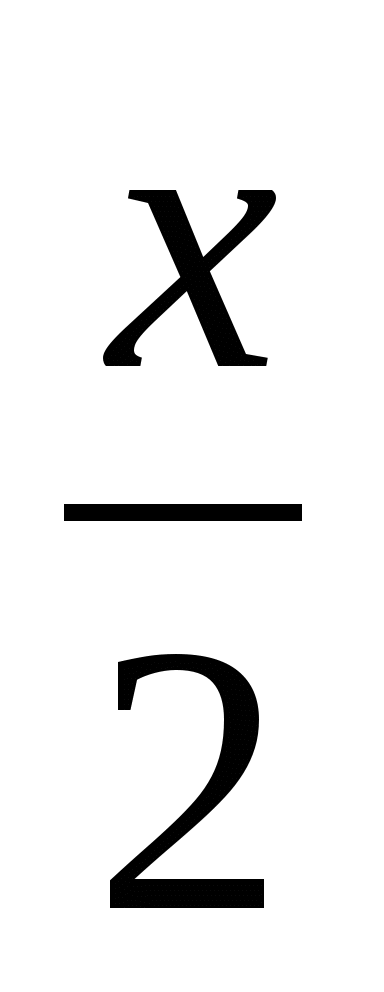
-
разложение на множители
-
решение простейших уравнений.
Ответ: х =2![]() п,
п
п,
п![]() z ,
х =
z ,
х = ![]() +
2
+
2![]() к,
к
к,
к![]() z.
z.
7. Самостоятельная работа.
Цель: провести текущий контроль за усвоением решения тригонометрических уравнений, определив тип уравнения и выбрав метод решения.
Самостоятельная работа на 10 вариантов по карточкам из газеты «Математика» №9 - 2004 стр. 12.( см. приложение).
8. Домашнее задание.
Цель: закрепить навыки решения тригонометрических уравнений. Подготовиться к зачету.
Домашнее задание на 12 вариантов по карточкам из газеты «Математика»
№1 -2002г. Стр.16. (см. приложение) и решить графически уравнение
sin х + cos х = 1
9. Итог урока.
-
Чем мы занимались сегодня на уроке?
-
Какие типы и методы решения тригонометрических уравнений мы знаем?
-
Оценка работы класса.
10. И напоследок притча:
«Однажды царь решил выбрать из своих придворных первого помощника. Он подвел их к огромному дверному замку. Кто откроет, тот и будет первым помощником. Никто не притронулся даже к замку. Лишь один визирь подошел и толкнул замок, который открылся. Он не был закрыт на ключ.
Ты получишь эту должность, потому что полагаешься не только на то, что видишь и слышишь, но надеешься, на собственные силы и не боишься сделать попытку».
Дополнение: зачет проводится так же по карточкам из газеты «Математика»
№18-2004г. Стр.16.
Рекомендации по использованию урока:
-
данный урок проводится перед зачетом и контрольной работой, как урок обобщения в 10классе по данной теме;
-
так же этот урок можно провести в 11 классе в разделе повторения;
3) так же можно отдельно провести урок по теме «Несколько способов решения уравнения sin х + cos х = 1», где повторяются многие методы решения тригонометрических уравнений.
Министерство образования Российской Федерации.
Конспект урока по теме: ![]()
Автор: В.Е.Агафонова
учитель математики
МОУ СОШ №6.
г. Усть-Кут
2006г.