- Учителю
- Рабочая программа по математике 6 класс
Рабочая программа по математике 6 класс
| МУНИЦИПАЛЬНОЕ КАЗЁННОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «БОЛЬШЕБАЩЕЛАКСКАЯ ОСНОВНАЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА» «ПРИНЯТО» Руководитель РМО ___________ Протокол №__ от | «УТВЕРЖДАЮ» Директор _____________ Л.В.Лубягина Приказ№ _____ от «___»______2014г
|
Рабочая программа
Математика 6 класс
Базовый уровень
На 2014-2015 учебный год.
Составитель:
учитель математики
Максимова И.П
7 разряд
с.Большой Бащелак 2014год
Пояснительная записка
Рабочая программа по математике для 6 класса составлена на основе федерального компонента государственного стандарта основного общего образования (приказ МОиН РФ от 05.03.2004г. № 1089), примерных программ по математике, примерного тематического планирования к учебному комплексу для 6 класса (авторы Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд.), Программа. Планирование учебного материала. Математика. 5-6 классы. Жохов В.И.- М.: Мнемозина, 2011. - 32 с. Федерального перечня учебников, рекомендованных Министерством образования Российской Федерации к использованию в образовательном процессе в общеобразовательных учреждениях, с учетом требований к оснащению образовательного процесса в соответствии с содержанием наполнения учебных предметов компонента государственного стандарта общего образования, базисного учебного плана.
Рабочая программа конкретизирует содержание предметных тем образовательного стандарта и даёт распределение учебных часов по разделам курса.
Программа рассчитана на 204часа, по 6 часов 34 недели.
Теоретический материал курса излагается на наглядно-интуитивном уровне, математические методы и законы формулируются в виде правил. Курс строится на индуктивной основе с привлечением дедуктивных рассуждений. Учебный процесс ориентирован на: рациональное сочетание устных и письменных видов работы как при изучении теории, так и при решении задач; сбалансированное сочетание традиционных и новых методов обучения; оптимизированное применение объяснительно-иллюстративных и эвристических методов; использование современных технических средств обучения.
Преобладающей формой текущего контроля выступает письменный (самостоятельные и контрольные работы) и устный опрос.
Для реализации учебной программы используется учебно-методический комплект, включающий:
1. Математика. 6 класс: учебник для общеобразовательных учреждений / Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. - М.: Мнемозина, 2010.
2.Программа. Планирование учебного материала. Математика. 5-6 классы. Жохов В.И.- М.: Мнемозина, 2011. - 32 с.
Цели программы обучения: систематическое развитие понятия числа; выработка умений выполнять устно и письменно арифметические действия над числами, переводить практические задачи на язык математики; подготовка учащихся к изучению систематических курсов алгебры и геометрии.
Задачи программы обучения:
- овладение конкретными математическими знаниями, необходимыми для применения в практической деятельности, для изучения смежных дисциплин;
- интеллектуальное развитие учащихся, формирование качеств мышления, характерных для математической деятельности;
- формирование представлений о математических идеях и методах;
- формирование преставлений о математике как части общечеловеческой культуры, понимания значимости математики для общественного прогресса.
Структура программы.
Рабочая программа состоит из двух разделов: «Содержание обучения», «Требования к математической подготовке учащихся». К программе прилагаются: тематическое и поурочное планирование учебного материала; учебно-методические средства обучения.
СОДЕРЖАНИЕ ОБУЧЕНИЯ
Арифметика
Числа и вычисления.
Делители и кратные числа. Признаки делимости. Простые и составные числа. Разложение числа на простые множители. Общее кратное. Нахождение НОД и НОК.
Основное свойство дроби. Сокращение дробей. Сравнение дробей. Арифметические действия с обыкновенными дробями. Нахождение части числа и числа по его части.
Отношения. Пропорции. Основное свойство пропорции.
Решение текстовых задач арифметическими приемами.
Положительные и отрицательные числа. Противоположные числа. Модуль числа. Целые числа. Сравнение чисел. Арифметические действия с положительными и отрицательными числами, свойства арифметических действий.
Рациональные числа. Применение свойств арифметических действий для рационализации вычислений.
Прикидка результатов вычислений.
Этапы развития представлений о числе.
Элементы алгебры
Алгебраические выражения. Буквенные выражения. Числовые подстановки в буквенные выражения. Простейшие преобразования выражений, раскрытие скобок, приведение подобных слагаемых.
Уравнения и неравенства. Уравнение с одной переменной. Корень уравнения. Примеры решения текстовых задач методом составления уравнений (алгебраическим способом).
Числовые неравенства.
Числовые функции. Таблицы и диаграммы. Графики реальных процессов.
Координаты. Изображение чисел точками на координатной прямой. Координата точки. Геометрический смысл модуля числа. Прямоугольная система координат. Абсцисса и ордината точки.
Элементы геометрии
Представление о начальных понятиях геометрии и геометрических фигурах.
Параллельные прямые. Перпендикулярные прямые. Многоугольники. Правильные многоугольники. Построение перпендикуляра к прямой и параллельных прямых с помощью угольника и линейки. Площадь круга.
Элементы комбинаторики
Множество. Элемент множества, подмножество. Примеры решения комбинаторных задач: перебор вариантов, правило умножения.
ТРЕБОВАНИЯ К МАТЕМАТИЧЕСКОЙ ПОДГОТОВКЕ УЧАЩИХСЯ
Числа и вычисления
В результате изучения курса математики учащиеся должны овладеть следующими умениями, представляющими минимум:
- правильно употреблять термины, связанные с различными видами чисел и способами их записи: целое, дробное, рациональное, положительное, отрицательное; переходить от одной формы записи к другой (например, представлять десятичную дробь в виде обыкновенной, проценты - в виде десятичной или обыкновенной дроби);
- производить в уме арифметические действия в пределах сложности примеров на сложение и вычитание двузначных чисел, умножение и деление нацело двузначного числа на однозначное;
- выполнять арифметические действия над обыкновенными дробями (включая обращение смешанного числа в обыкновенную дробь, нахождение общего знаменателя дробей, сокращение дробей и представление их в виде смешанных чисел);
- выполнять арифметические действия с рациональными числами, сочетать при вычислениях устные и письменные приемы;
- сравнивать числа, упорядочивать наборы чисел; понимать связь отношений «больше» и «меньше» с расположением точек на координатной прямой;
- составлять и решать пропорции, решать основные задачи на дроби, проценты;
- округлять натуральные числа и десятичные дроби, производить прикидку результата вычислений.
Выражения и их преобразования
В результате изучения курса математики учащиеся должны овладеть следующими умениями, представляющими минимум:
- правильно употреблять термины «выражение», «числовое выражение», «буквенное выражение», «значение выражения», понимать их использование в тексте, в речи учителя, понимать формулировку заданий: «упростить выражение», «найти значение выражения», «разложить на множители»;
- составлять несложные буквенные выражения и формулы; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления; выражать из формул одни переменные через другие;
- находить значение степени с натуральным показателем.
Уравнения и неравенства
В результате изучения курса математики учащиеся должны овладеть следующими умениями, представляющими минимум:
- понимать, что уравнения - это математический аппарат решения разнообразных задач по математике, смежных областей знаний, практики;
- правильно употреблять термины «уравнение», «неравенство», «корень уравнения»; понимать их в тексте, в речи учителя, понимать формулировку задания «решить уравнение»;
- читать числовые неравенства (в том числе и двойные);
- решать линейные уравнения с одной переменной;
- составлять линейные уравнения по условиям текстовых задач.
Функции
В результате изучения курса математики учащиеся должны овладеть следующими умениями, представляющими минимум:
-познакомиться с примерами зависимостей между реальными величинами (прямая и обратная пропорциональности, линейная функция);
- познакомиться с координатной плоскостью, знать порядок записи координат точек плоскости и их названий, уметь построить координатные оси, отметить точку по заданным координатам, определить координаты точки, отмеченной на координатной плоскости;
- находить в простейших случаях значения функций, заданных формулой, таблицей, графиком;
- интерпретировать в несложных случаях графики реальных зависимостей между величинами, отвечая на поставленные вопросы.
Геометрические фигуры и их свойства. Измерение геометрических величин
В результате изучения курса математики учащиеся должны овладеть следующими умениями, представляющими минимум:
- распознавать на чертежах и моделях геометрические фигуры (отрезки, прямые, лучи, углы, многоугольники, окружности, круги); изображать указанные геометрические фигуры; выполнять чертежи по условию задачи;
- владеть практическими навыками использования геометрических инструментов (линейки, угольника, транспортира, циркуля) для изображения фигур, а также для нахождения длин отрезков и величин углов;
- решать задачи на вычисление геометрических величин (длин, углов, площадей, объемов), применяя свойства фигур и формулы.
ПЛАНИРОВАНИЕ УЧЕБНОГО МАТЕРИАЛА
ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ
6 класс
(6 ч в неделю, всего 204 ч)
1. Делимость чисел(24 ч)
Делители и кратные натурального числа. Общий делитель и общее кратное. Признаки делимости на 2, 3, 5, 9, 10. Простые и составные числа. Разложение натурального числа на множители.
Основная цель: завершить изучение натуральных чисел, подготовить основу для освоения действий с обыкновенными дробями.
В данной теме завершается изучение вопросов, связанных с натуральными числами. Основное внимание должно быть уделено знакомству с понятиями «делитель» и «кратное», а также «общий делитель» и «общее кратное», которые находят применение при сокращении обыкновенных дробей и при их приведении к общему знаменателю. Упражнения полезно выполнять с опорой на таблицу умножения - прямым подбором.
Определенное внимание уделяется знакомству с признаками делимости, понятию простого и составного числа. При их изучении целесообразно формирование умений проводить простейшие умозаключения, обосновывая свои действия ссылками на определение, правило.
У учащихся должно быть сформировано умение раскладывать число на множители. Умение разложить число на простые множители не относится к числу обязательных.
Рассматриваются простейшие комбинаторные задачи.
2. Сложение и вычитание дробей с разными знаменателями(26 ч)
Основное свойство дроби. Сокращение дробей. Приведение дробей к общему знаменателю. Понятие о наименьшем общем знаменателе нескольких дробей. Сравнение дробей. Сложение и вычитание дробей с произвольными знаменателями. Решение текстовых задач.
Основная цель: выработать прочные навыки преобразования дробей, сложения и вычитания дробей.
Одним из важнейших результатов изучения данной темы является усвоение основного свойства дроби, применяемого для преобразования дробей: сокращения, приведения к новому знаменателю. При этом рекомендуется излагать материал без опоры на понятия НОД и НОК. Умение приводить дроби к общему знаменателю используется для сравнения дробей.
При рассмотрении действий с дробями используются правила сложения и вычитания дробей с одинаковыми знаменателями, понятие смешанного числа. Все эти вопросы целесообразно повторить с учащимися. Важно обратить внимание на случай вычитания дроби из целого числа.
3. Умножение и деление обыкновенных дробей(38ч)
Умножение и деление обыкновенных дробей. Основные задачи на дроби.
Основная цель: выработать прочные навыки арифметических действий с обыкновенными дробями и решения основных задач на дроби.
В этой теме завершается работа над формированием навыков арифметических действий с обыкновенными дробями. Навыки должны быть достаточно прочными, чтобы учащиеся не испытывали затруднений в вычислениях с рациональными числами, чтобы алгоритмы действий с обыкновенными дробями могли стать в дальнейшем опорой для формирования умений выполнять действия с алгебраическими дробями.
При изучении данной темы учащиеся должны усвоить, что для обращения обыкновенной дроби в десятичную достаточно разделить (если это возможно) числитель на знаменатель. В каждом конкретном случае они должны знать, в какую дробь обращается данная обыкновенная дробь - в конечную или бесконечную. При этом не обязательно акцентировать внимание на том, что бесконечная дробь является периодической. Учащиеся должны знать представление в виде десятичной дроби таких дробей, как 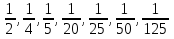 .
.
Все рассмотренные алгоритмы, включая умножение дроби на натуральное число и умножения смешанных чисел, должны быть хорошо отработаны.
Расширение аппарата действий с дробями позволяет решать текстовые задачи, в которых требуется найти дробь от числа или число по данному значению его дроби.
4. Отношения и пропорции(22 ч)
Пропорция. Основное свойство пропорции. Решение задач с помощью пропорции. Понятия о прямой и обратной пропорциональности величин. Задачи на пропорции. Масштаб. Формулы длины окружности и площади круга. Шар.
Основная цель: сформировать понятия пропорции, прямой и обратной пропорциональности величин.
Необходимо, чтобы учащиеся усвоили основное свойство пропорции, так как оно находит применение на уроках математики, физики, химии. В частности, достаточное внимание должно быть уделено решению с помощью пропорции задач на проценты.
Понятия о прямой и обратной пропорциональности величин можно сформировать как обобщение нескольких конкретных примеров, подчеркнув при этом практическую значимость этих понятий, возможность их применения для упрощения решения соответствующих задач.
В данной теме даются представления о длине окружности и площади круга. Соответствующие формулы к обязательному материалу не относятся. Рассмотрение геометрических фигур завершается знакомством с шаром.
5. Положительные и отрицательные числа(17ч)
Положительные и отрицательные числа. Противоположные числа. Модуль числа и его геометрический смысл. Сравнение чисел. Целые числа. Понятие о рациональном числе. Изображение чисел на координатной прямой. Координата точки.
Основная цель: расширить представления учащихся о числе путем введения отрицательных чисел.
Целесообразность введения отрицательных чисел показывается на содержательных примерах. Учащиеся должны научиться изображать положительные и отрицательные числа на координатной прямой. В дальнейшем она будет служить наглядной основой для правил сравнения чисел, сложения и вычитания чисел.
Специальное внимание должно быть уделено усвоению вводимого здесь понятия модуля числа, прочное знание которого необходимо для формирования умения сравнивать отрицательные числа, а в дальнейшем и для овладения алгоритмами арифметических действий с положительными и отрицательными числами.
6. Сложение и вычитание положительных и отрицательных чисел(13 ч)
Сложение и вычитание положительных и отрицательных чисел.
Основная цель: выработать прочные навыки сложения и вычитания положительных и отрицательных чисел.
Действия с отрицательными числами вводятся на основе представлений об изменении величин.Сложение и вычитание чисел иллюстрируется соответствующими перемещениями точек координатной прямой. При изучении данной темы отрабатываются алгоритмы сложения и вычитания при выполнении действий с целыми и дробными числами.
7. Умножение и деление положительных и отрицательных чисел(15 ч)
Умножение и деление положительных и отрицательных чисел. Понятие о рациональном числе. Десятичное приближение обыкновенной дроби. Применение законов арифметических действий для рационализации вычислений.
Основная цель: выработать прочные навыки арифметических действий с положительными и отрицательными числами.
Действие умножения с отрицательными числами вводится на основе представлений об изменении величин. Правила деления отрицательных чисел вводятся. Исходя из смысла определений соответствующих действий.
Навыки умножения и деления положительных и отрицательных чисел отрабатываются сначала при выполнении отдельных действий, а затем в сочетании с навыками сложения и вычитания при вычислении значений числовых выражений.
8. Решение уравнений(17ч)
Простейшие преобразования выражений: раскрытие скобок, приведение подобных слагаемых. Решение линейных уравнений. Примеры решения текстовых задач с помощью линейных уравнений.
Основная цель: подготовить учащихся к выполнению преобразований выражений, решению уравнений.
Навыки преобразования буквенных выражений отрабатываются лишь в той степени, в которой они необходимы для решения несложных уравнений.
Введение арифметических действий над отрицательными числами позволяет ознакомить учащихся с общими приемами решения линейных уравнений с одним неизвестным путем переноса слагаемых из одной части уравнения в другую, приведения подобных слагаемых, деления обеих частей уравнения на коэффициент при неизвестном. Следует иметь в виду, что в дальнейшем метод составления уравнений становится основным методом решения задач.
9. Координаты на плоскости(16 ч)
Построение перпендикуляра к прямой и параллельных прямых с помощью чертежного угольника и линейки. Прямоугольная система координат на плоскости, абсцисса и ордината точки. Примеры графиков, диаграмм.
Основная цель: познакомить учащихся с прямоугольной системой координат на плоскости.
Созданию представлений о перпендикулярных и параллельных прямых служат наблюдения окружающей обстановки. Учащиеся должны научиться распознавать и изображать параллельные перпендикулярные прямые. Основное внимание следует уделить отработке навыков их построения с помощью линейки и угольника, не требуя воспроизведения точных определений, обоснования единственности построения и т.п.
Основным результатом знакомства учащихся с координатной плоскостью должны явиться знания порядка записи координат точки плоскости и их названий, умения строить точку по заданным координатам, определять координаты точки, расположенной на координатной плоскости. Этот материал необходим для построения и чтения эмпирических графиков, отдельные примеры которых рассматриваются в теме.
Формированию вычислительных и графических умений способствует построение столбчатых диаграмм. При выполнении соответствующих упражнений найдут применение изученные ранее сведения о масштабе и округлении чисел.
10. Повторение. Решение задач (16 ч)
Делимость чисел. Действия с обыкновенными дробями и смешанными числами. Отношения пропорции. Действия с рациональными числами. Решение уравнений. Координаты на плоскости.
Тематические и итоговые контрольные работы:
-
Контрольная работа № 1 «Делимость чисел»
-
Контрольная работа № 2 «Сложение и вычитание дробей с разными знаменателями.»
-
Контрольная работа № 3 «Сложение и вычитание смешанных чисел»
-
Контрольная работа № 4 «Умножение обыкновенных дробей»
-
Контрольная работа № 5 «Деление обыкновенных дробей»
-
Контрольная работа № 6 «Деление и умножение обыкновенных дробей. Дробные выражения»
-
Контрольная работа № 7 «Отношения и пропорции»
-
Контрольная работа № 8 «Масштаб. Окружность и круг»
-
Контрольная работа № 9 «Противоположные числа»
-
Контрольная работа № 10 «Сложение и вычитание положительных и отрицательных чисел»
-
Контрольная работа № 11 «Умножение и деление положительных и отрицательных чисел »
-
Контрольная работа № 12 «Упрощение выражений»
-
Контрольная работа № 13 «Решение уравнений»
-
Контрольная работа № 14 «Координаты на плоскости»
-
Контрольная работа № 15 «Итоговая»
Учебно-тематический план
№
Название темы
Количество часов
1
Делимость чисел
24
2
Сложение и вычитание дробей с разными знаменателями
26
3
Умножение и деление обыкновенных дробей
38
4
Отношения и пропорции
22
5
Положительные и отрицательные числа
17
6
Сложение и вычитание положительных и отрицательных чисел
13
7
Умножение и деление положительных и отрицательных чисел
15
8
Решение уравнений
17
9
Координаты на плоскости
16
10
Повторение. Решение задач
16
Итого:
204
УЧЕБНО-МЕТОДИЧЕСКИЕ СРЕДСТВА ОБУЧЕНИЯ
-
Депман И.Я. За страницами учебника математики: книга для чтения учащимися 5 - 6 классов / И.Я. Депман, Н.Я. Виленкин. - М.: Просвещение, 1999. - 288 с.
-
Жохов В.И. Программа. Планирование учебного материала. Математика. 5-6 классы. - М.: Мнемозина, 2011. - 32 с.
-
Жохов В.И. Преподавание математики в 5 - 6 классах: методическое пособие. - М.: Мнемозина, 2008. - 239 с.
-
Жохов В.И. Математика. 6 класс. Контрольные работы для учащихся общеобразовательных учреждений / В.И. Жохов, Л.Б. Крайнева. - М.: Мнемозина, 2010. - 63 с.
-
Жохов В.И. Математика. 6 класс. Диктанты для учащихся общеобразовательных учреждений / В.И. Жохов, А.А. Терехова. - М.: Мнемозина, 2010.
-
ЖоховВ.И. Математический тренажер, 6 класс / В.И. Жохов, В.Н. Погодин. - М: Мнемозина, 2009 г. - 48 с.
-
Кузнецова Г.М. Программы для общеобразовательных школ, гимназий, лицеев. Математика, 5 - 11 кл. / Г.М. Кузнецова, Н.Г. Миндюк. - 4-е изд., стереотип. М.: Дрофа, 2004. - 320с.
-
Лысенко Ф.Ф. Тесты для промежуточной аттестации. Математика, 5-6 класс / Ф.Ф. Лысенко, Л.С. Ольхова, С.Ю. Кулабухов. - Ростов-на-Дону: Легион, 2010. - 157 с.
-
Математика. 6 класс: учебник для общеобразовательных учреждений / Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. - М.: Мнемозина, 2010. - 288 с.
-
Попова Л.П. Контрольно-измерительные материалы. 6 класс. - М.: ВАКО, 2010. - 93 с.
-
Чесноков А.С. Дидактические материалы по математике для 6 класса / А.С. Чесноков, К.И. Нешков. - М: Классикс Стиль, 2009. - 165 с.
ПРИЛОЖЕНИЕ 1
Критерии и нормы оценки знаний, умений и навыков обучающихся
Оценка устных ответов учащихся по математике
Ответ оценивается отметкой «5», если ученик:
-
полностью раскрыл содержание материала в объеме, предусмотренном программой и учебником
-
изложил материал грамотным языком в определенной логической последовательности, точно используя математическую терминологию и символику
-
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу
-
показал умение иллюстрировать теоретические положения конкретными примерами, применять их в новой ситуации при выполнении практического задания
-
продемонстрировал усвоение ранее изученных сопутствующих вопросов, сформированность и устойчивость используемых при отработке умений и навыков
-
отвечал самостоятельно без наводящих вопросов учителя
-
возможны одна-две неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил по замечанию учителя
-
учащийся демонстрирует полное понимание сути теории и свободно оперирует ей, творчески применяет теоретические знания на практике
-
при решении задач наблюдаются четко осознанные действия
-
решает нестандартные задачи
-
не допускает вычислительных ошибок
-
умеет самостоятельно получать знания, работая с дополнительной литературой (учебником, компьютером, справочной литературой)
Ответ оценивается отметкой «4», если он удовлетворен в основном требованиям на оценку «5», но при этом имеет один из недостатков:
-
в изложении допущены небольшие пробелы, не исказившие математическое содержание ответа
-
допущены один-два недочета при освещении основного содержания ответа, исправленные по замечанию учителя
-
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные по замечанию учителя
-
без использования собственного плана, новых примеров
-
без применения знаний в новой ситуации
-
без использования связей с ранее изученным материалом, усвоенным при изучении других предметов
-
незадумываясь решает задачи по известному алгоритму
-
проявляет способность к самостоятельным выводам
-
допускает вычислительные ошибки крайне редко
Ответ оценивается отметкой «3», ставится в следующих случаях:
-
неполно или непоследовательно раскрыто содержание материала, но показано общее понимание вопроса и продемонстрированы умения, достаточные для дальнейшего усвоения программного материала
-
имелись затруднения или допущены ошибки в определении понятий, использовании математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя
-
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме
-
при изложении теоретического материала выявлена недостаточная сформированность основных умений и навыков
-
учащийся запомнил большую часть теоретического материала, без которого невозможна практическая работа по теме
-
решает самостоятельно только те практические задачи, в которых известен алгоритм, а остальные задания может выполнить только с помощью учителя и учащихся
-
допускает много вычислительных ошибок
Ответ оценивается отметкой «2», ставится в случаях:
-
не раскрыто основное содержание учебного материала
-
обнаружено незнание или непонимание учеником большей или наиболее важной части учебного материала
-
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя
-
ученик обнаружил полное незнание или непонимание изучаемого учебного материала или не смог ответить ни на один из поставленных вопросов по изучаемому материалу.
Оценка письменных ответов учащихся по математике
Отметка «5» ставится, если:
-
работа выполнена верно и полностью
-
в логических рассуждениях и обосновании решения нет пробелов и ошибок
-
решение не содержит неверных математических утверждений (возможна одна неточность, описка, не являющаяся следствием незнания или непонимания учебного материала)
Отметка «4» ставится, если:
-
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновать рассуждения не являлось специальным объектом проверки)
-
допущена одна или две-три недочета в выкладках, рисунках, чертежах или графиках (если эти виды работы не являлись (специальным объектом проверки)
-
выполнено без недочетов не менее ¾ заданий
Отметка «3» ставится, если:
-
допущены более одной ошибки или более трех недочетов в выкладках, чертежах или графиках, но учащийся владеет обязательными умениями по проверяемой теме
-
без недочетов выполнено не менее половины работы
Отметка «2» ставится, если:
-
не раскрыто основное содержание учебного материала
-
обнаружено незнание или непонимание учеником большей или наиболее важной части учебного материала
-
допущены существенные ошибки, показавшие, что учащийся не владеет обязательными умениями по проверяемой теме в полном объеме
-
правильно выполнено менее половины работы
-
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах, графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя
-
работа показала полное отсутствие у учащегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно
Учитель может повысить отметку:
-
за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося
-
за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий
Общая классификация ошибок
При оценке знаний, умений и навыков обучающихся следует учитывать все ошибки (грубые и негрубые) и недочёты.
Грубыми считаются ошибки:
-
незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения
-
незнание наименований единиц измерения
-
неумение выделить в ответе главное
-
неумение применять знания, алгоритмы для решения задач
-
неумение делать выводы и обобщения
-
неумение читать и строить графики
-
неумение пользоваться первоисточниками, учебником и справочниками
-
потеря корня или сохранение постороннего корня
-
отбрасывание без объяснений одного из них
-
равнозначные им ошибки
-
вычислительные ошибки, если они не являются опиской
-
логические ошибки
К негрубым ошибкам следует отнести:
-
неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными
-
неточность графика
-
нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными)
-
нерациональные методы работы со справочной и другой литературой
-
неумение решать задачи, выполнять задания в общем виде
Недочетами являются:
-
нерациональные приемы вычислений и преобразований
-
небрежное выполнение записей, чертежей, схем, графиков
ПРИЛОЖЕНИЕ 2
ОСНОВНЫЕ ПОНЯТИЯ 6 КЛАССА
-
Абсцисса точки
-
Вычитание дробей
-
Вычитание отрицательных и положительных чисел
-
Вычитание смешанных чисел
-
Граф
-
График
-
График движения
-
Деление дробей
-
Деление отрицательных и положительных чисел
-
Деление смешанных чисел
-
Делитель
-
Диаграмма круговая
-
Диаграмма столбчатая
-
Длина окружности
-
Дополнительный множитель
-
Дробное выражение
-
Дробь несократимая
-
Дробь периодическая
-
Золотое сечение
-
Координата точки на плоскости
-
Координата точки на прямой
-
Координатная плоскость
-
Координатная прямая
-
Коэффициент
-
Кратное
-
Линейное уравнение
-
Масштаб
-
Модуль числа
-
Наибольший общий делитель
-
Наименьшее общее кратное
-
Наименьший общий знаменатель
-
Нахождение дроби числа
-
Нахождение нескольких процентов числа
-
Нахождение процентного отношения
-
Нахождение числа по его дроби
-
Неравенство нестрогое
-
Неравенство строгое
-
Общий знаменатель
-
Ордината точки
-
Основное свойство дроби
-
Основное свойство пропорции
-
Ось абсцисс
-
Ось ординат
-
Отношение
-
Отношения взаимно обратные
-
Параллельные лучи
-
Параллельные отрезки
-
Параллельные прямые
-
Перпендикулярные лучи
-
Перпендикулярные отрезки
-
Перпендикулярные прямые
-
Пирамида
-
Площадь круга
-
Подобные слагаемые
-
Приведение дроби к новому знаменателю
-
Призма
-
Признаки делимости на 2, 5 и10; 3, 9
-
Пропорциональная зависимость прямая
-
Пропорциональная зависимость обратная
-
Пропорция
-
Разложение на множители
-
Разложение на простые множители
-
Раскрытие скобок
-
Решение уравнений
-
Свойства действий с рациональными числами
-
Система координат на плоскости
-
Сложение дробей
-
Сложение отрицательных и положительных чисел
-
Сложение подобных слагаемых
-
Сложение смешанных чисел
-
Сокращение дробей
-
Сравнение дробей
-
Сравнение отрицательных и положительных чисел
-
Сфера
-
Умножение дробей
-
Умножение отрицательных и положительных чисел
-
Умножение смешанных чисел
-
Цилиндр
-
Цифры нечетные
-
Цифры четные
-
Числа-близнецы
-
Числа взаимно обратные
-
Числа взаимно простые
-
Числа дружественные
-
Числа нечетные
-
Числа отрицательные
-
Числа положительные
-
Числа простые
-
Числа противоположные
-
Числа рациональные
-
Числа совершенные
-
Числа составные
-
Числа фигурные
-
Числа целые
-
Числа четные
-
Шар
-
Шара диаметр
Шара радиус