- Учителю
- Сборник занимательных задач по математике для 3-5 классов
Сборник занимательных задач по математике для 3-5 классов
СБОРНИК ЗАНИМАТЕЛЬНЫХ ЗАДАЧ
ПО МАТЕМАТИКЕ
ДЛЯ ОБУЧАЮЩИХСЯ ( 3 - 5 классов)
Автор: Беглова Наталья Михайловна, учитель математики
МКОУ «Коровяковская СОШ» Алексеевский филиал.
Пособие предназначено для учащихся 3- 5 х классов общеобразовательных школ, желающих расширить и углубить свои знания и умения в математике как школьной, так и олимпиадной.
Предлагаемое учебное пособие в определенной мере отражает опыт занятий по математике со школьниками младших и средних классов и включает в себя задачи, которые могут быть условно разнесены на три раздела: - углубление школьного курса; - факультативный материал; - олимпиадные задачи начального уровня.
.
Задача 1. (Слайд 2)
8 деревьев растут в ряд на расстоянии 3 метра друг от друга.
Каково расстояние между двумя крайними деревьями?
Решение: 7 * 8 = 48
Ответ: 48 метров
Задача 2. (Слайд 3)
Как за одну секунду увеличить число 86 на 12, не производя сложения?
Решение: написать на листочке 86 и перевернуть его, получим 98.
Задача 3. (Слайд 4)
Попробуйте нарисовать 2 квадрата так, чтобы все 9 песиков оказались
в отдельных боксах.
Условие:  Решение :
Решение : 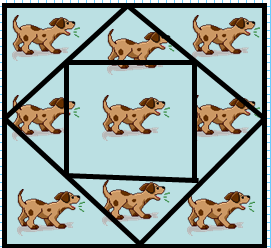
Задача 4. (Слайд 5)
Разложи на столе 7 монет в 5 рядов по 3 монеты в каждом. Ряды могут идти
в любом направлении.
Решение : 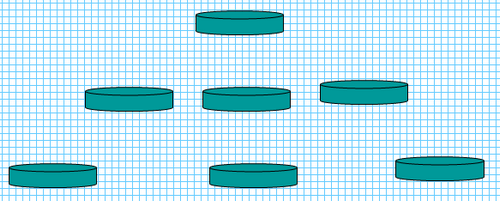
Задача 5. (Слайд 6)
4 карандаша и 3 линейки стоят 54 руб., 2 карандаша и 2 линейки - 34 руб. Сколько стоят: а) 8 карандашей и 7 линеек?
б) 8 карандашей и 4 линейки?
Решение: а) Если 2 карандаша и 2 линейки стоят 34 руб., то 4 кар. и 4 лин. - 68 руб. Тогда 8 каран. и 7 лин. - 122 руб. ( 54 + 68 = 122)
б) т.к. 2 кар и 1 лин стоят 20 руб (54 - 34 = 20) , то 8 кар и 4 лин стоят 80 руб
( 20 * 4 = 80)
Задача 6. (Слайд 7)
10 учебников на 240 р. дороже, чем 30 тетрадей. Те же 10 учебников на 120 р. дороже, чем 40 таких же тетрадей. Сколько стоит 1 учебник и одна тетрадь?
Решение: из условия ясно, что 10 тетрадей стоят ( 40 - 30 = 10) 120 р. ( 240 - 120 = 120) Следовательно 1 тет стоит 12 р.
10 учебников стоят ( 240 + 12 * 30 = 600 ) , 1 учебник 60 р.
Ответ: 1 тетрадь стоит 12 рублей, 1 учебник стоит 60 рублей.
Задача 7. (Слайд 8)
В оранжерее были срезаны гвоздики: желтых и розовых - 40 шт, розовых и красных - 30 шт, красных и желтых - 44 шт. Сколько гвоздик каждого цвета было срезано в оранжерее?
Решение: (40 + 30 + 44 ) : 2 = 57 всего срезали цветов.
57 - 30 = 27 гвоздик желтых
40 - 27 = 13 гвоздик розовых
30 - 13 = 17 гвоздик красных
Задача 8. (Слайд 9)
Встретились три друга: скульптор Белов, скрипач Чернов, художник Рыжов:
«Замечательно, что один из нас блондин, другой брюнет, а третий рыжеволосый, но ни у одного нет волос такого цвета, на который указывает его фамилия», заметил брюнет. «Ты прав», - сказал Белов. Какой цвет волос у художника?
Решение: Таблица на слайде
Задача 9. (Слайд 10)
Три подруги вышли в белом, зеленом и синем платьях. Их туфли также были белого, зеленого и синего цветов. Известно, что только у Ани цвет платья и туфель совпадали. Ни платье, ни туфли Вали не были белыми, Наташа была в зеленых туфлях.
Определите цвет платья и туфель каждой из подруг.
Решение: Таблица на слайде
Задача 10. (Слайд 11)
В футбольном турнире участвовали 7 команд. Каждый с каждым сыграл по одной партии.
Сколько партий они сыграли?
Решение : 6+5+4+3+2+1=21
Ответ: 21партия
Задача 11. (Слайд 12)
Семь человек обменялись фотографиями. Сколько при этом было роздано фотографий?
Решение : Каждый раздал 6 фото (всем, кроме себя), а всего 7 * 6 = 42
Ответ: 42 фотографии.
Задача 12. (Слайд 12)
По столбу высотой 10 м взбирается улитка. За день она поднимается по столбу на 5 м, за ночь опускается на 4 м. Сколько дней ей потребуется, чтобы подняться на вершину столба?
Решение : За первый день улитка поднимется на 5 м, а за ночь опустится на 4 м. Следовательно, за первые сутки она окажется на высоте 1 м; 5м пройдет за 5 суток. На 6 день улитка достигнет вершины.
Ответ: 6 дней
Задача 13. (Слайд 13)
В один сосуд входит 3 л, а в другой - 5 л. Как с помощью этих сосудов налить в кувшин 4 л воды из водопроводного крана?
Решение: Налить воду в сосуд 5 л и перелить в сосуд 3л, в сосуде останется 2 л, их то и перелить в кувшин, и так повторить еще раз.
Задача 14. (Слайд 13)
Есть 5 обрывков цепи, в каждом из которых 3 кольца. Как соединить их в одну цепь, расклепав и заклепав лишь три кольца?
Решение: рассоединить 3 последних.
Задача15. (Слайд 13)
Как рассадить 45 кроликов в 9 клеток так, чтобы во всех клетках было разное
количество кроликов?
Решение: посадим в первую клетку 1 кролика, во вторую - 2, в третью - три и т.д. Имеем: 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45 кроликов.
Задача 16. (Слайд 14)
Велосипедист собирается проехать из пункта А в пункт Е, в который ведут три маршрута: через В, через С и через D . Расстояния в километрах между соседними городами показаны на схеме. Известно, что если ехать через В, то средняя скорость будет равна 16 км/ч, если ехать через D, то средняя скорость будет равна 18 км/ч, а если ехать через С, то средняя скорость будет равна 20 км/ч. Исходя из этих данных, велосипедист выбрал маршрут так, чтобы доехать до Е за наименьшее время. Сколько часов он планирует пробыть в пути?
Решение: 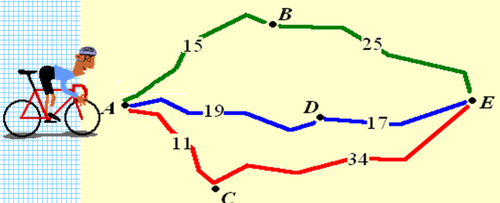
(15 + 25) : 16 = 2,5 ч
(19 + 17) : 18 = 2 ч
(11 + 34) : 16 = 2,25 ч
Ответ: 2 часа
Задача 17. (Слайд 15)
В пяти ящиках лежит по одинаковому числу яблок. Если из каждого ящика вынуть 60 яблок, то во всех ящиках останется столько яблок, сколько раньше их было в двух ящиках. Сколько яблок было в каждом ящике?
Решение: Если из каждого ящика вынуть 60 яблок, то будет вынуто 300 яблок ( 60 * 5 = 300 ) Так как по условию остается яблок столько, сколько было в двух ящиках, то вынуто столько, сколько было в 3 ящиках. Значит. В каждом ящике было 100 яблок
( 300 : 3 = 100 )
Ответ: 100 яблок
Задача 18. (Слайд 16)
Рыбак поймал рыбу. Когда у него спросили, сколько весит пойманная рыба, он сказал: «Я думаю, что хвост ее весит 1 кг, голова весит столько, сколько хвост и половина туловища, а туловище - сколько голова и хвост вместе». Сколько же весит рыба?
У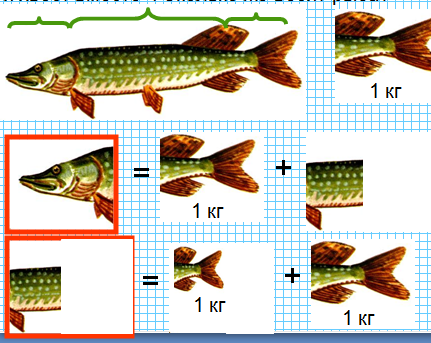 словие:
словие:
Решение:
1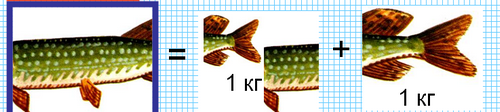 )
)
2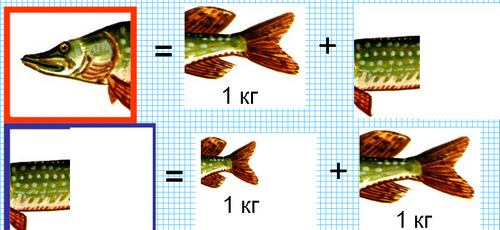 )
)
Ответ: голова - 3кг, туловище - 4кг, хвост - 1кг. Итого- 8 кг
Задача 19. (Слайд 17)
Четыре чёрные коровы и три рыжие дают за 5 дней столько молока, сколько три чёрные коровы и пять рыжих дают за 4 дня. У каких коров больше удои, у чёрных или у рыжих? Подсказка:
Заметьте, из условия следует, что за день 20 чёрных коров и 15 рыжих дают столько же молока, сколько 12 чёрных и 20 рыжих.
Решение:
Наше условие, по существу, означает, что 20 чёрных коров и 15 рыжих дают за день столько же молока, сколько 12 чёрных и 20 рыжих. А это значит, что 8 чёрных коров дают молока столько же, сколько 5 рыжих. Отсюда заключаем, что у рыжих коров удои больше.
Ответ: у рыжих.
Задача 20. (Слайд 18)
Заполните свободные клетки "шестиугольника" (см. рисунок) целыми числами от 1 до 19, чтобы во всех вертикальных и диагональных рядах сумма чисел, стоящих в одном ряду, была бы одна и та же.
Подсказка:
Попробуйте определить сумму чисел в ряду, тогда вы сможете расставить по местам несколько чисел. Затем попробуйте определить, какое число стоит в центральной клетке.
Р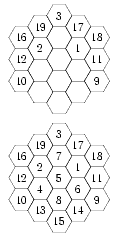 ешение:
ешение:
Поскольку один из рядов таблицы заполнен, то можно определить сумму ряда - она равна 38. Теперь можно расставить числа во многих клетках. Осталось 7 пустых клеток, в которых должны быть расположены числа 4, 5, 6, 8, 13, 14, 15. Рассмотрим диагональ, на которой расположены числа 10, 1, 18.
Две пустые клетки на ней должны занимать два числа с суммой 9. Это могут быть только 4 и 5. Теперь рассмотрим ту диагональ, на которой расположены числа 16, 2, 9. Две пустые клетки на ней должны занимать два числа с суммой 11. Это могут быть только 5 и 6. Значит, в центре стоит 5, а вторые числа на диагоналях - соответственно 4 и 6. Теперь уже можно однозначно заполнить всю таблицу.
Задача 21. (Слайд 19)
В коробке синие, красные и зелёные карандаши. Всего 20 штук. Синих в 6 раз больше, чем зелёных, красных меньше, чем синих. Сколько в коробке красных карандашей? Подсказка:
Подумайте, сколько может быть синих карандашей.
Решение:
Значит, синих и зелёных вместе - 7 или 14. Синих, соответственно, 6 или 12, а зелёных - 1 или 2. Поскольку всего карандашей 20, то для красных осталось две возможности: либо их 20 - 7 = 13, либо 20 - 14 = 6. Но красных меньше, чем синих, значит, единственный возможный ответ: 12 синих карандашей, 2 зелёных и 6 красных.
Ответ: 6 красных карандашей.
Задача 22. (Слайд 19)
Если Аня идёт в школу пешком, а обратно едет на автобусе, то всего на дорогу она тратит 1,5 ч. Если же она едет на автобусе в оба конца, то весь путь у неё занимает 30 мин. Сколько времени потратит Аня на дорогу, если и в школу и из школы она будет идти пешком?
Подсказка:
Сколько времени займёт путь в один конец на автобусе? А сколько - путь в один конец пешком?
Решение:
Путь в оба конца на автобусе занимает 30 мин, следовательно, путь в один конец на автобусе займёт 15 мин. На дорогу в один конец пешком понадобится 1,5 ч-15 мин, т.е. 1 ч 15 мин. Значит, на дорогу пешком в оба конца Аня тратит 2, 5 ч.
Ответ: 2,5 ч.
Задача 23. (Слайд 20)
Волк и заяц бежали наперегонки. Заяц весь путь бежал с одной и той же скоростью, а волк первую половину пути бежал вдвое быстрее, чем заяц, а вторую половину - вдвое медленней, чем заяц. Кто победил?
Подсказка:
Заметьте, на вторую половину пути волк потратил ровно столько времени, сколько заяц потратил на весь.
Решение:
На вторую половину пути волк потратил ровно столько времени, сколько заяц на весь путь. А ведь сколько-то времени у волка ушло и на первую половину пути. Так что победил заяц.
Ответ: заяц
Задача 24. (Слайд 21)
Шрек сел в поезд. Проехав половину всего пути, он лёг спать и спал до тех пор, пока не осталось проехать половину того пути, который он проспал. Какую часть всего пути Шрек проехал бодрствующим? Шрек сел в поезд. Проехав половину всего пути, он лёг спать и спал до тех пор, пока не осталось проехать половину того пути, который он проспал. Какую часть всего пути Шрек проехал бодрствующим?
Подсказка:
Можно, конечно, представить условие задачи в виде уравнения, но лучше обойтись без этого.
Решение:
Обозначим через s отрезок пути, который Буратино проехал от того момента, как проснулся, до конца. Тогда путь, который Буратино проспал, составит 2s. Всего же от момента, как Буратино заснул, он проехал путь 2s + s = 3s. Но известно, что это - половина всего пути. Значит, длина всего пути 6s. Поскольку же бодрствующим Буратино проехал путь 4s, то по отношению ко всему пути эта часть составит ![]() =
= ![]() .
.
Ответ: 2/3 пути.
Задача 25. (Слайд 22)
У Пятачка и Вини-Пуха был велосипед, на котором они отправились в соседнюю деревню. Ехали по очереди, но всякий раз, когда один ехал, другой шёл пешком, а не бежал. При этом они ухитрились прибыть в деревню почти в 2 раза быстрее, чем если бы оба шли пешком. Как им это удалось?
Подсказка:
Попробуйте организовать путешествие так, чтобы и Буратино и Пьеро ровно полдороги проехал на велосипеде.
Решение:
Вини-Пух проехал на велосипеде полдороги, слез с него и дальше пошёл пешком. А Пятачок первую половину пути прошёл пешком, затем дошёл до велосипеда, сел на него и поехал. Таким образом, они и сэкономили время.
Ответ: Вини-Пух проехал полдороги на велосипеде, и, оставив его, дальше пошёл пешком. Пятачок дошёл до велосипеда, сел на него и проехал вторую половину пути.
Задача 26. (Слайд 23)
На лужайке росли 35 жёлтых и белых одуванчиков. После того как 8 белых облетели, а 2 жёлтых побелели, жёлтых одуванчиков стало вдвое больше, чем белых. Сколько белых и сколько жёлтых одуванчиков росло на лужайке вначале?
Подсказка: Сколько одуванчиков осталось на лужайке после того, как 8 белых облетели?
Решение: Когда 8 белых одуванчиков облетели, на лужайке осталось 27 одуванчиков - 18 жёлтых и 9 белых. Значит, вначале на лужайке росли 18 + 2 = 20 жёлтых и 9 + 8 - 2 = 15 белых одуванчиков.
Ответ: 20 жёлтых и 15 белых одуванчиков.
Задача 27. (Слайд 24)
Руслан и Людмила. «Идет направо - песнь заводит, налево - сказку говорит». Чтобы рассказать сказку, ученому Коту требуется 5 минут, а чтобы спеть песню - 4 минуты. В десять часов утра Кот начал рассказывать сказку. Куда будет идти Кот в полдень? Подсказка:
Вспомните: «Идет направо - песнь заводит».
Решение:
Чтобы рассказать сказку и спеть песню ученому Коту требуется 4 + 5 = 9 мин. За 2 часа с 10 утра до полудня пройдет 120 мин. 120 = 9 · 13 + 3. Значит, за это время Кот успеет спеть 13 песен, рассказать 13 сказок, и у него останется 3 мин на то, чтобы начать (но не успеть кончить), рассказывать сказку. А это значит, что в полдень Кот будет идти налево.
Ответ: в полдень Кот будет идти налево
Задача 28. (Слайд 25)
Попробуйте быстро найти сумму всех цифр в этой таблице:
7
8
2
6
9
5
4
7
6
9
2
6
2
1
3
3
2
8
4
1
5
6
3
4
1
8
4
8
9
7
6
4
7
5
8
7
3
8
1
8
7
1
5
6
7
4
6
3
5
2
3
7
2
9
2
3
9
5
4
3
1
4
9
2
4
6
9
2
9
6
8
9
5
9
5
9
6
1
8
6
4
1
8
1
4
2
1
5
1
5
Подсказка:
Обратите внимание, ведь нигде не сказано, что нельзя изменить порядок суммирования.
Решение:Рассмотрим суммы чисел не по строкам, а по столбцам. Две последовательные цифры в столбцах дают в сумме 10, значит, сумма цифр в любом столбце будет 30. А всего столбцов 15. Значит, сумма всех цифр равна 450.
Ответ : Достаточно просчитать числа "по столбцам". Ответ: 450.
Задача 29. (Слайд 26)
Имеются двое песочных часов - на 7 минут и на 11 минут. Яйцо варится 15 минут. Как отмерить это время при помощи имеющихся часов?
Подсказка:
Заметьте, с помощью двух разных песочных часов можно отмерить не только время, равное их "сумме", но и время, равное их "разности".
Решение:
"Включим" одновременно двое часов. Когда 7минутные часы пересыпятся, перевернём их и дадим сыпаться 4 минуты, до окончания пересыпания 11минутных часов. Если теперь перевернуть 7 минутные часы, они будут сыпаться ровно 4 минуты, а всего часы "сыпались" 15 минут, что и требовалось.
Задача 30. (Слайд 26)
Отличник Поликарп заполнил клетки таблицы цифрами так, что сумма цифр, стоящих в любых трех соседних клетках, равнялась 15, а двоечник Колька стёр почти все цифры. Сможете ли вы восстановить таблицу?
![]()
Подсказка:Любые два числа, стоящие на расстоянии трех клеток друг от друга, равны между собой. Подумайте, почему.
Решение:
Поскольку сумма чисел, стоящих в любых трех соседних клетках, постоянна, значит, равны между собой все числа, стоящие на местах 1, 4, 7,..., т.е. на этих местах стоит 6. Также равны между собой все числа, стоящие на местах 3, 6, 9,..., значит, на всех этих местах стоит 4. Числа, стоящие на местах 2, 5, 8,... тоже равны между собой и должны быть равны 5, чтобы соблюдалось условие о сумме 15. Окончательное решение приведено в таблице.
![]()
Ответ 6, 5, 4, 6, 5, 4, 6, 5, 4, 6, 5, 4, 6, 5, 4.
Задача 31. (Слайд 27)
На поляну прилетело 35 ворон. Неожиданно вороны взлетели и разделились на две стаи: одна стая уселась на ветви старой берёзы, а другая - на ольху. Через некоторое время с берёзы на ольху перелетело 5 ворон, столько же ворон совсем улетело с берёзы, после чего на берёзе осталось вдвое больше ворон, чем на ольхе. Сколько ворон было в каждой из двух стай первоначально?
Подсказка:
Попробуйте представить условие задачи системой уравнений. Подумайте, как решить эту задачу, не составляя системы уравнений.
Решение:
С поляны улетели 5 ворон, а остались 30. Поскольку при этом на берёзе их стало в два раза больше, чем на ольхе, значит, на берёзе оказалось 20 ворон, а на ольхе - 10. Но до этого на ольху с берёзы перелетели 5 ворон, следовательно, сначала на ольхе было 5 ворон. А с берёзы 5 ворон улетели на ольху и 5 ворон улетели совсем, т.е. на берёзе было 30 ворон.
Ответ: 30 и 5 ворон.
Задача 32. (Слайд 28)
Два лесоруба, Иван и Прохор, работали вместе в лесу и сели перекусить. У Ивана было 4 лепешки, а у Прохора - 8. Тут к ним подошел охотник.
- Вот, братцы, заблудился в лесу, до деревни далеко, а есть очень хочется. Пожалуйста, поделитесь со мной хлебом-солью!
- Ну что ж, садись, чем богаты, тем и рады, - сказали лесорубы.
Двенадцать лепешек были разделены поровну на троих. После еды охотник пошарил в карманах, нашел гривенник и полтинник и сказал:
- Не обессудьте, братцы, больше ничего нет. Поделитесь, как знаете!
Охотник ушел, а лесорубы заспорили. Прохор говорит: - По-моему, деньги надо разделить поровну! А Иван ему возражает: - За 12 лепешек - 60 к., значит за каждую лепешку по 5 к. Раз у тебя было 8 лепешек - тебе 40 к., у меня 4 лепешки - мне 20 к.! А как бы Вы разделили эти деньги между лесорубами?
Подсказка: Обратите внимание, на каждого едока приходится по 4 лепешки.
Решение:
Ошибаются и Иван и Прохор. На каждого едока пришлось по 4 лепешки, следовательно, Иван съел все свои лепешки сам, а Прохор половину своих лепешек отдал охотнику. Это означает, что все 60 к. должен получить Прохор.
Задача 33. (Слайд 29)
В зоомагазине продают больших и маленьких птиц. Большая птица стоит вдвое дороже маленькой. Одна дама купила 5 больших птиц и 3 маленьких, а другая - 5 маленьких и 3 больших. При этом первая дама заплатила на 20 рублей больше. Сколько стоит каждая птица?
Подсказка: Попробуйте выразить разницу покупок двух дам «в маленьких птицах».
Решение:
Первая дама за свою покупку заплатила, как за 13 маленьких птиц (напомним, что большая птица в два раза дороже маленькой), а вторая - как за 11 маленьких. Т.е. разница в покупках - 2 маленькие птицы, а разница в цене - 20 руб. Значит, маленькая птица стоит 10 руб., а большая - 20 руб.
Задача 34. (Слайд 30)
7 волков съедают 7 баранов за 7 дней. За сколько дней 9 волков съедят 9 баранов? Подсказка:Подумайте, сколько времени нужно одному волку, чтобы съесть одного барана.
Решение:
Семь волков съедают семь баранов за семь дней, значит один волк съедает одного барана за семь дней. А девять волков съедят девять баранов за те же семь дней.
Задача 35. (Слайд 30)
Без ореха (от дупла до орешника) белка бежит со скоростью 4 м/сек, а с орехом (от орешника до дупла) - со скоростью 2 м/сек. На путь от дупла до орешника и обратно она тратит 54 секунды. Найдите расстояние от дупла до орешника. Ответ обоснуйте.
Решение:
Поскольку обратно белка бежит в два раза медленнее, то время, затраченное белкой на обратную дорогу, в два раза больше времени, которое она тратит на дорогу от дупла до орешника. Поэтому время, затраченное на дорогу от дупла до орешника, в три раза меньше времени, затраченного на всю дорогу, то есть равно 54 : 3 = 18 секунд. Следовательно, расстояние от дупла до орешника равно 18 * 4 = 72 метра.
Ответ: 72 метра.
Задача 36. (Слайд 31)
Петя и Вася участвовали в велогонке. Все участники стартовали одновременно и показали на финише различное время. Петя финишировал сразу после Васи и оказался на десятом месте. Сколько человек участвовало в гонке, если Вася был пятнадцатым с конца? Решение:
Так как Петя оказался на десятом месте, а Вася финишировал перед ним, то Вася занял девятое место. Вася был пятнадцатым с конца, значит за ним финишировало еще четырнадцать человек. Следовательно, в гонке участвовало 23 человека.
Ответ: 23 человека.
Задача 37. (Слайд 31)
Коля и его сестра Маша пошли в гости. Пройдя четверть пути, Коля вспомнил, что они забыли дома подарок и повернул обратно, а Маша пошла дальше. Маша пришла в гости через 20 минут после выхода из дома. На сколько минут позже пришел в гости Коля, если известно, что они все время шли с одинаковыми скоростями?
Решение:Так как Коля возвращался домой, то прошел "лишнюю" половину пути. Значит, время опоздания равно половине времени, потраченного на весь путь, то есть равно 10 минутам.
Ответ: на 10 минут.
Задача 38. (Слайд 32)
Волк с тремя поросятами написал детектив "Три поросёнка--2", а потом вместе с Красной Шапочкой и её бабушкой кулинарную книгу "Красная Шапочка-2". В издательстве выдали гонорар за обе книжки поросёнку Наф-Нафу. Он забрал свою долю и передал оставшиеся 2100 золотых монет Волку. Гонорар за каждую книгу делится поровну между её авторами. Сколько денег Волк должен взять себе?
Решение:
За книгу "Три поросёнка-2" каждый автор должен получить четверть гонорара. Но так как Наф-Наф свою долю уже забрал, Волку причитается 1/3 остатка. За книгу "Красная шапочка-2" ему также полагается 1/3 гонорара. Поэтому всего он должен получить треть переданной ему суммы.
Ответ: 700 золотых монет.
Задача 39. (Слайд 33)
Имеется квадратный пруд. По углам его близ воды растут 4 дерева. Пруд понадобилось увеличить, сохранив , однако, квадратную форму . Но деревья трогать не желают. Можно ли увеличить площадь пруда, сохранив квадратную форму? И причём так увеличить ,чтобы 4 дерева, оставаясь на своих местах ,не были затоплены водой ,а стояли у берегов нового пруда?
У
 словие: Решение:
словие: Решение:
Задача 40. (Слайд 34)
На узкой дороге встретились машины. Дорога была так узка, что разъехаться
невозможно. Однако в месте встречи есть заезд, где помещается только 1машина. Помоги разъехаться машинам, чтобы двигаться дальше в том же порядке.
Решение: на слайде.
Задача 41. (Слайд 35)
Почти 2 недели ходил охотник по лесу, проверяя капканы. В хижине
у него были керосиновая лампа, очаг и дровяная печурка, но у охотника
осталась всего 1 спичка. Как вы думаете, что он зажжет в
первую очередь?
Ответ: спичку
Задача 42. (Слайд 36)
У меня было 3 целых яблока, 4 половинки да 8 четвертинок.
Сколько всего яблок было у меня?
Ответ: 7 яблок
Литература:
Книга для учителя « Занимательные задания в обучении математике»
Год выпуска: 1994 Автор: Шуба М.Ю. Издательство: Просвещение