- Учителю
- Планирование математика 7 класс
Планирование математика 7 класс
Пояснительная записка
Рабочая программа по математике составлена на основе следующих нормативных документов:
-
Закона РФ «Об образовании»
-
Федеральный государственный компонент государственного образовательного стандарта начального общего, основного общего и среднего (полного) образования (Приложение к приказу Минобразования России от 5 марта 2004 года №1089).
-
Учебного плана МБОУ СОШ №11 г. Брянска на 2016-2017 учебный год.
-
Программы общеобразовательных учреждений. Алгебра 7-9 классы. Бурмистрова Т.А. М., «Просвещение», 2014.
-
Программы общеобразовательных учреждений. Геометрия 7-9 классы. Бурмистрова Т.А. М., «Просвещение», 2010.
Общая характеристика учебного предмета
Математика - единая наука: арифметика, алгебра, геометрия, тригонометрия, начала математического анализа и так далее являются зависимыми друг от друга дисциплинами. Единое изложение всего предмета подчеркивает широту математических идей и общность развиваемых методов. Математика тесно связана с различными науками. Моделирование окружающих нас явлений и изучение возникающих моделей позволяет предсказывать результаты, которые не всегда можно проверить экспериментально. В этом состоит одна из главных задач математики, а поэтому систематическое рассмотрение практических задач играет важную роль в процессе обучения.
Математика является важным элементом общей человеческой культуры и в значительной мере - одним из видов искусства. По словам Б. Рассела, «математика владеет не только истиной, но и высшей красотой - красотой холодной и суровой, подобной красоте скульптуры». Использование увлекательных задач позволяет подчеркнуть красоту математики и помогает сделать преподавание математики живым и менее формальным. Математика имеет свои законы развития и в силу того, что разрабатывает математический аппарат, который может применяться в различных сферах человеческой деятельности, носит абстрактный характер. Умение абстрактно мыслить вырабатывается постепенно, опираясь на конкретные реальные объекты. А так как восприятие мира в значительной степени зависит от психологических особенностей человека, то в процессе обучения математике приходится учитывать как образный, так и рациональный типы мышления. Многие математические понятия и методы не могут быть восприняты сразу. Необходим долгий и трудный путь к осознанному пониманию вопроса. Поэтому важное значение имеет обучение по «спирали», когда систематическое возвращение к фундаментальным математическим понятиям позволяет постепенно переходить от наблюдений и экспериментов к точным формулировкам и доказательствам.
В связи с природными различиями в склонностях и способностях целесообразно проводить преподавание математики по нескольким уровням требований к знаниям и умениям. Первый уровень - общегуманитарный - предполагает овладение таким минимумом знаний, который необходим каждому культурному человеку. Второй уровень - технологический - должен обеспечить умения и навыки, которые позволят успешно продолжить обучение в старшей школе, а в последующем и вузе. Третий уровень- специализированный. На этом уровне следует стремиться к воспитанию профессионального интереса к математике и сознательному овладению логикой рассуждений, что необходимо для обучения на математическом или близких к нему естественнонаучных профилях старшей школы, осуществляя тем самым подготовку к последующему обучению на математическом или близким к нему естественнонаучных фа культетах университетов.
Описание места учебного предмета в учебном плане
В соответствие с учебным планом школы (34 учебных недели), программа рассчитана на 170 часа в год (5 часов в неделю).
Цель и задачи учебного предмета
Цели:
формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей.
-
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
-
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;
-
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
-
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса;
-
развитие вычислительных и формально-оперативных алгебраических умений до уровня, позволяющего уверенно использовать их при решении задач математики и смежных предметов (физика, химия, основы информатики и вычислительной техники), усвоение аппарата уравнений и неравенств как основного средства математического моделирования прикладных задач, осуществление функциональной подготовки школьников. В ходе изучения курса, учащиеся овладевают приёмами вычислений на калькуляторе.
-
овладение системой геометрических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования.
Задачи:
-
развить логическое мышление и речь - умение логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контр примеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства.
В ходе освоения содержания курса учащиеся получают возможность:
-
развить представление о числе и роли вычислений в человеческой практике; сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;
-
овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;
-
изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
-
развить пространственные представления и изобразительные умения, освоить основные факты и методы планиметрии, познакомиться с простейшими пространственными телами и их свойствами;
-
получить представления о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;
-
развить логическое мышление и речь - умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контр примеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
-
сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.
-
овладение приемами аналитико-синтетической деятельности при доказательстве теории и решении задач;
-
обращение к примерам из практики, что развивает умения, учащихся вычленять геометрические факты, формы и отношения в предметах и явлениях действительности, использовали язык геометрии для их описания, приобретали опыт исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;
-
ясного, точного, грамотного изложения своих мыслей в устной и письменной речи; проведения доказательных рассуждений, аргументаций, выдвижения гипотез и их обоснования; поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.
Учебно-тематический план
-
Содержание тем учебного курса
1. Выражения, тождества, уравнения (22 ч)
Числовые выражения с переменными. Простейшие преобразования выражений. Уравнение, корень уравнения. Линейное уравнение с одной переменной. Решение текстовых задач методом составления уравнений. Статистические характеристики.
Основная цель: систематизировать и обобщить сведения о преобразованиях алгебраических выражений и решении уравнений с одной переменной.
Первая тема курса 7 класса является связующим звеном между курсом математики 5-6 классов и курсом алгебры. В ней закрепляются вычислительные навыки, систематизируются и обобщаются сведения о преобразованиях выражений и решении уравнений.
Нахождение значений числовых и буквенных выражений даёт возможность повторить с обучающимися правила действий с рациональными числами. Умения выполнять арифметические действия с рациональными числами являются опорными для всего курса алгебры. Следует выяснить, насколько прочно овладели ими учащиеся, и в случае необходимости организовать повторение с целью ликвидации выявленных пробелов. Развитию навыков вычислений должно уделяться серьезное внимание и в дальнейшем при изучении других тем курса алгебры.
В связи с рассмотрением вопроса о сравнении значений выражений расширяются сведения о неравенствах: вводятся знаки ≥ и ≤, дается понятие о двойных неравенствах.
При рассмотрении преобразований выражений формально-оперативные умения остаются на том же уровне, учащиеся поднимаются на новую ступень в овладении теорией. Вводятся понятия «тождественно равные выражения», «тождество», «тождественное преобразование выражений», содержание которых будет постоянно раскрываться и углубляться при изучении преобразований различных алгебраических выражений. Подчеркивается, что основу тождественных преобразований составляют свойства действий над числами.
Усиливается роль теоретических сведений при рассмотрении уравнений. С целью обеспечения осознанного восприятия обучающимися алгоритмов решения уравнений вводится вспомогательное понятие равносильности уравнений, формулируются и разъясняются на конкретных примерах свойства равносильности. Дается понятие линейного уравнения и исследуется вопрос о числе его корней. В системе упражнений особое внимание уделяется решению уравнений вида ах=b при различных значениях, а и b. Продолжается работа по формированию у обучающихся умения использовать аппарат уравнений как средство для решения текстовых задач. Уровень сложности задач здесь остается таким же, как в 6 классе.
Изучение темы завершается ознакомлением обучающихся с простейшими статистическими характеристиками: средним арифметическим, модой, медианой, размахом. Учащиеся должны уметь пользовать эти характеристики для анализа ряда данных в несложных ситуациях.
2. Начальные геометрические сведения (10 ч)
Простейшие геометрические фигуры: прямая, точка, отрезок, луч, угол. Понятие равенства геометрических фигур. Сравнение отрезков и углов. Измерение отрезков, длина отрезка. Измерение углов, градусная мера угла. Смежные и вертикальные углы, их свойства. Перпендикулярные прямые.
Основная цель - систематизировать знания учащихся о простейших геометрических фигурах и их свойствах; ввести понятие равенства фигур.
В данной теме вводятся основные геометрические понятия и свойства простейших геометрических фигур на основе наглядных представлений, учащихся путем обобщения очевидных или известных из курса математики 1-6 классов геометрических фактов. Понятие аксиомы на начальном этапе обучения не вводится, и сами аксиомы не формулируются в явном виде. Необходимые исходные положения, на основе которых изучаются свойства геометрических фигур, приводятся в описательной форме. Принципиальным моментом данной темы является введение понятия наложения. Определенное внимание должно уделяться практическим приложениям геометрических понятий.
3. Функции (11 ч)
Функция, область определения функции. Вычисление значений функции по формуле. График функции. Прямая пропорциональность и ее график. Линейная функция и её график.
Основные цели: ознакомить обучающихся с важнейшими функциональными понятиями и с графиками прямой пропорциональности и линейной функции общего вида.
Данная тема является начальным этапом в систематической функциональной подготовке обучающихся. Здесь вводятся такие понятия, как функция, аргумент, область определения функции, график функции. Функция трактуется как зависимость одной переменной от другой. Учащиеся получают первое представление о способах задания функции. В данной теме начинается работа по формированию у обучающихся умений находить по формуле
значение функции по известному значению аргумента, выполнять ту же задачу по графику и решать по графику обратную задачу. Функциональные понятия получают свою конкретизацию при изучении линейной функции и ее частного вида - прямой пропорциональности. Умения строить и читать графики этих функций широко используются как в самом курсе алгебры, так и в курсах геометрии и физики. Учащиеся должны понимать, как влияет знак коэффициента на расположение в координатной плоскости графика функции у=кх, где к
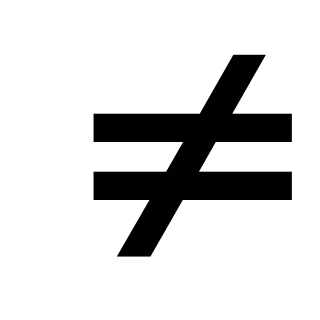 0, как зависит от значений к
и b взаимное расположение графиков двух функций вида у=кх+b.
0, как зависит от значений к
и b взаимное расположение графиков двух функций вида у=кх+b.
Формирование всех функциональных понятий и выработка соответствующих навыков, а также изучение конкретных функций сопровождаются рассмотрением примеров реальных зависимостей между величинами, что способствует усилению прикладной направленности курса алгебры.
4. Треугольники (17ч)
Треугольник. Признаки равенства треугольников. Перпендикуляр к прямой. Медианы, биссектрисы и высоты треугольника. Равнобедренный треугольник и его свойства. Задачи на построение с помощью циркуля и линейки.
Основная цель - ввести понятие теоремы; выработать умение доказывать равенство треугольников с помощью изученных признаков; ввести новый класс задач - на построение с помощью циркуля и линейки.
Признаки равенства треугольников являются основным рабочим аппаратом всего курса геометрии. Доказательство большей части теорем курса и также решение многих задач проводится по следующей схеме: поиск равных треугольников - обоснование их равенства с помощью какого-нибудь признака - следствия, вытекающего из равенства треугольников. Применение признаков равенства треугольников при решении задач дает возможность постепенно накапливать опыт проведения доказательных рассуждений. На начальном этапе изучения и применения признаков равенства треугольников целесообразно использовать задачи с готовыми чертежами.
5. Степень с натуральным показателем (11ч)
Степень с натуральным показателем и ее свойства. Одночлен. Функции у=х2, у=х3 и их графики.
Основная цель: выработать умение выполнять действия над степенями с натуральными показателями.
В данной теме дается определение степени с натуральным показателем. В курсе математики 6 класса учащиеся уже встречались с примерами возведения чисел в степень. В связи с вычислением значений степени в 7 классе дается представление о нахождении значений степени с помощью калькулятора; рассматриваются свойства степени с натуральным показателем: на примере доказательства свойств аm · аn = аm+n; аm : аn = аm-n, где m > n; (аm)n = аm·n; (ab)m = ambm учащиеся впервые знакомятся с доказательствами, проводимыми на алгебраическом материале. Указанные свойства степени с натуральным показателем находят применение при умножении одночленов и возведении одночленов в степень. При нахождении значений выражений содержащих степени, особое внимание следует обратить на порядок действий.
Рассмотрение функций у=х2, у=х3 позволяет продолжить работу по формированию умений строить и читать графики функций. Важно обратить внимание обучающихся на особенности графика функции у=х2:график проходит через начало координат, ось Оу является его осью симметрии, график расположен в верхней полуплоскости.
Умение строить графики функций у=х2 и у=х3 используется для ознакомления обучающихся с графическим способом решения уравнений.
6. Параллельные прямые (13 ч)
признаки параллельности прямых. Аксиома параллельных прямых. Свойства параллельных прямых.
Основная цель - ввести одно из важнейших понятий - понятие параллельных прямых; дать первое представление об аксиомах и аксиоматическом методе в геометрии; ввести аксиому параллельных прямых.
Признаки и свойства параллельных прямых, связанные с углами, образованными при пересечении двух прямых секущей (накрест лежащими, односторонними, соответственными), широко используются в дальнейшем при изучении четырехугольников, подобных треугольников, при решении задач, а также в курсе стереометрии.
7. Многочлены (17 ч)
Многочлен. Сложение, вычитание и умножение многочленов. Разложение многочленов на множители.
Основные цели: выработать умение выполнять сложение, вычитание, умножение многочленов и разложение многочленов на множители.
Данная тема играет фундаментальную роль в формировании умения выполнять тождественные преобразования алгебраических выражений. Формируемые здесь формально-оперативные умения являются опорными при изучении действий с рациональными дробями, корнями, степенями с рациональными показателями.
Изучение темы начинается с введения понятий многочлена, стандартного вида многочлена, степени многочлена. Основное место в этой теме занимают алгоритмы действий с многочленами - сложение, вычитание и умножение. Учащиеся должны понимать, что сумму, разность, произведение многочленов всегда можно представить в виде многочлена. Действия сложения, вычитания и умножения многочленов выступают как составной компонент в заданиях на преобразования целых выражений. Поэтому нецелесообразно переходить к комбинированным заданиям прежде, чем усвоены основные алгоритмы.
Серьезное внимание в этой теме уделяется разложению многочленов на множители с помощью вынесения за скобки общего множителя и с помощью группировки.
Соответствующие преобразования находят широкое применение как в курсе 7 класса, так и в последующих курсах, особенно в действиях с рациональными дробями.
В данной теме учащиеся встречаются с примерами использования рассматриваемых преобразований при решении разнообразных задач, в частности при решении уравнений. Это позволяет в ходе изучения темы продолжить работу по формированию умения решать уравнения, а также решать задачи методом составления уравнений. В число упражнений включаются несложные задания на доказательство тождества.
8. Соотношения между сторонами и углами треугольника (18 ч)
Сума углов треугольника. Соотношение между сторонами и углами треугольника. Неравенство треугольника. Прямоугольные треугольники, их свойства и признаки равенства. Расстояние от точки до прямой. Расстояние между параллельными прямыми. Построение треугольника по трем элементам.
Основная цель - рассмотреть новые интересные и важные свойства треугольников.
В данной теме доказывается одна из важнейших теорем геометрии - теорема о сумме углов треугольника. Она позволяет дать классификацию треугольников по углам (остроугольный, прямоугольный, тупоугольный), а также установить некоторые свойства и признаки равенства прямоугольных треугольников.
Понятие расстояния между параллельными прямыми вводится на основе доказанной предварительно теоремы о том, что все точки каждой из двух прямых параллельных прямых равноудалены от другой прямой. Это понятие играет важную роль, в частности используется в задачах на построение.
При решении задач на построение в 7 классе следует ограничиться только выполнением и описанием построения искомой фигуры. В отдельных случаях можно провести устно анализ и доказательство, а элементы исследования должны присутствовать лишь тогда, когда это оговорено условием задачи.
9. Формулы сокращенного умножения (19 ч)
Формулы (а - b )(а + b ) = а2 - b 2, (а ± b)2 = а2± 2а b + b2, (а ± b)3 = а3 ± За2b + За b2 ± b3, (а ± b) (а2
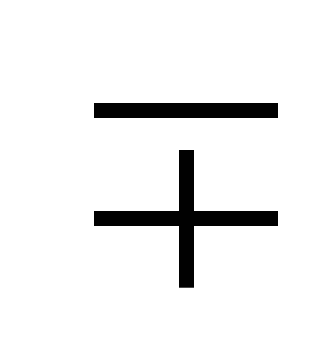 а
b + b2) = а3 ± b3. Применение
формул сокращённого умножения в преобразованиях выражений.
а
b + b2) = а3 ± b3. Применение
формул сокращённого умножения в преобразованиях выражений.
Основные цели: выработать умение применять формулы сокращенного умножения в преобразованиях целых выражений в многочлены и в разложении многочленов на множители.
В данной теме продолжается работа по формированию у обучающихся умения выполнять тождественные преобразования целых выражений. Основное внимание в теме уделяется формулам (а - b)(а + b) = а2 - b 2, (а ± b)2 = а2± 2а b + b2. Учащиеся должны знать эти формулы и соответствующие словесные формулировки, уметь применять их как «слева направо», так и «справа налево». Наряду с указанными рассматриваются также формулы (а ± b)3 = а3 ± За2b + За b2 ± b3, (а ± b) (а2
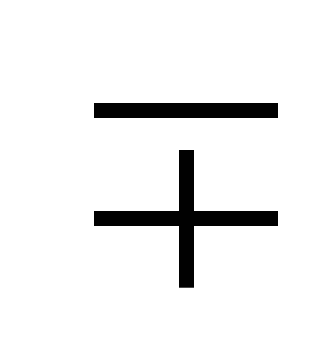 а b + b2) =
а3 ± b3. Однако они находят меньшее
применение в курсе, поэтому не следует излишне увлекаться
выполнением упражнений на их использование.
а b + b2) =
а3 ± b3. Однако они находят меньшее
применение в курсе, поэтому не следует излишне увлекаться
выполнением упражнений на их использование.
В заключительной части темы рассматривается применение различных приемов разложения многочленов на множители, а также использование преобразований целых выражений для решения широкого круга задач.
10. Системы линейных уравнений (16 ч)
Система уравнений. Решение системы двух линейных уравнений с двумя переменными и его геометрическая интерпретация. Решение текстовых задач методом составления систем уравнений.
Основные цели: ознакомить обучающихся со способом решения систем линейных уравнений с двумя переменными, выработать умение решать системы уравнений и применять их при решении текстовых задач.
Изучение систем уравнений распределяется между курсами 7 и 9 классов. В 7 классе вводится понятие системы и рассматриваются системы линейных уравнений.
Изложение начинается с введения понятия «линейное уравнение с двумя переменными». В систему упражнений включаются несложные задания на решение линейных уравнений с двумя переменными в целых числах.
Формируется умение строить график уравнения ах + bу=с, где а≠0 или b≠0, при различных значениях а, b, с. Введение графических образов даёт возможность наглядно исследовать вопрос о числе решений системы двух линейных уравнений с двумя переменными. Основное место в данной теме занимает изучение алгоритмов решения систем двух линейных уравнений с двумя переменными способом подстановки и способом сложения. Введение систем позволяет значительно расширить круг текстовых задач, решаемых с помощью аппарата алгебры. Применение систем упрощает процесс перевода данных задачи с обычного языка на язык уравнений.
11.Повторение по геометрии (10ч)
Основная цель - повторение и систематизация материала 7 класса
12. Повторение по алгебре (6 ч)
Основные цели: Повторение, обобщение и систематизация знаний, умений и навыков за курс алгебры 7 класса.
Требования к математической подготовке учащихся 7 класса
В результате изучения курса алгебры ученик должен:
знать/понимать
-
существо понятия математического доказательства; примеры доказательств;
-
существо понятия алгоритма; примеры алгоритмов;
-
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
-
как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
-
как потребности практики привели математическую науку к необходимости расширения понятия числа;
-
вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;
уметь
-
составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;
-
выполнять основные действия со степенями с натуральными показателями, с многочленами; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
-
решать линейные уравнения, решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;
-
изображать числа точками на координатной прямой;
-
определять координаты точки плоскости, строить точки с заданными координатами;
-
находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
-
применять графические представления при решении уравнений, систем, неравенств;
-
описывать свойства изученных функций (у=кх, где к
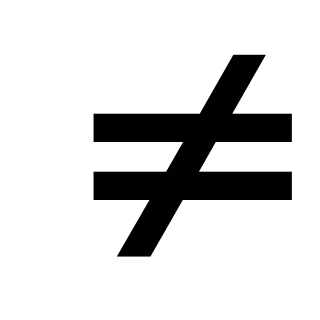 0,
у=кх+b, у=х2, у=х3), строить их
графики.
0,
у=кх+b, у=х2, у=х3), строить их
графики.
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных материалах;
-
описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;
-
интерпретации графиков реальных зависимостей между величинами.
-
выстраивания аргументации при доказательстве (в форме монолога и диалога);
-
распознавания логически некорректных рассуждений;
-
записи математических утверждений, доказательств;
-
анализа реальных числовых данных, представленных в виде диаграмм, графиков, таблиц;
-
решения практических задач в повседневной и профессиональной деятельности с использованием действий с числами, процентов, длин, площадей, объемов, времени, скорости;
-
решения учебных и практических задач, требующих систематического перебора вариантов;
-
понимания статистических утверждений.
В результате изучения курса геометрии ученик должен
знать/понимать:
-
существо понятия математического доказательства; приводить примеры доказательств;
-
каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждения о них, важных для практики;
уметь:
-
пользоваться языком геометрии для описания предметов окружающего мира;
-
распознавать геометрические фигуры, различать их взаимное расположение;
-
распознавать на чертежах и моделях геометрические фигуры (отрезки, углы, треугольники и их частные виды); изображать указанные геометрические фигуры;
-
выполнять чертежи по условию задачи;
-
владеть практическими навыками использования геометрических инструментов для изображения фигур, а также для нахождения длин отрезков и величин углов;
-
уметь решать несложные задачи на вычисление геометрических величин (длин, углов), опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, алгебраический аппарат;
-
проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования;
-
владеть алгоритмами решения основных задач на построение;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
описания реальных ситуаций на языке геометрии;
-
решения геометрических задач;
-
решения практических задач, связанных с нахождением геометрических величин (используя при необходимости справочники и технические средства);
-
построений геометрическими инструментами (линейка, угольник, циркуль, транспортир).
Литература.
Учебно-методический комплект:
-
Алгебра, учебник для 7 класса для общеобразовательных учреждений / Ю.Н. Макарычев, Н.Г. Миндюк, К.И.Нешков, С.Б. Суворова : Просвещение, 2006.
-
Геометрия, 7 - 9. Учебник для общеобразовательных учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.: Просвещение, 2010.
-
Алгебра. Дидактические материалы. 7 класс / Л. И. Звавич, Л. В. Кузнецова, С. Б. Суворова. - М.: Просвещение, 2015. - 159 с.: ил.
-
Дидактические материалы по геометрии для 7 класса / Б.Г. Зив, В.М. Мейлер: Просвещение, 2010.
Дополнительная учебно-методическая литература:
-
Алгебра: элементы статистики и теории вероятностей. Учебное пособие для учащихся 7 - 9 классов общеобразовательных учреждений / / Ю.Н. Макарычев, Н.Г. Миндюк: Просвещение, 2004.
-
Изучение алгебры в 7 - 9 классах. Книга для учителя. / Ю.Н. Макарычев, Н.Г. Миндюк: Просвещение, 2008.
-
Изучение геометрии в 7 - 9 классах. Методические рекомендации к учебнику. Книга для учителя / Л.С. Атанасян, В.Ф. Бутузов, Ю.А. Глазков: Просвещение, 2009.
-
Самостоятельные и контрольные работы по алгебре и геометрии для 7 класса / А.П. Ершова, В.В. Голобородько, А.С. Ершов: Илекса, 2010.
-
Задачи и упражнения на готовых чертежах. 7 - 9 классы. Геометрия / Е.М. Рабинович: Илекса, 2001.
-
Разноуровненвые дидактические материалы по алгебре. 7 класс / М.Б. Миндюк, Н.Г. Миндюк: Издательский Дом «Генжер», 2010.
Источники информации для учителя
-
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия, 7-9: учеб. для общеобразоват. учреждений. - М. : Просвещение, 2009. - 384 с. : ил.
-
Афанасьева Т. Л., Тапилина Л. А. Геометрия. 7 класс: поурочные планы по учебнику Л. С. Атанасяна и др. «Геометрия. 7-9 классы» - 3-е изд., исправлен. - Волгоград: Учитель, 2009. - 110 с.
-
Алтынов П. И. Тесты по алгебре: к учебнику под ред. С. А. Теляковского «Алгебра. 7 класс» - М.: ЭКЗАМЕН, 2008. - 94, [2] с.
-
Бурмистрова Т.А. Программы общеобразовательных учреждений. Алгебра. 7-9 классы. - М.: Просвещение, 2008 г.
-
Бурмистрова Т.А. Программы общеобразовательных учреждений. Геометрия. 7-9 классы. - М.: Просвещение, 2008 г.
-
Гаврилова Н.Ф. Поурочные разработки по геометрии: 7 класс. - М.: ВАКО, 2007. - 304 с. - (В помощь школьному учителю).
-
Ерина Т. М. Поурочное планирование по алгебре: 7 класс: к учебнику Ю. Н. Макарычева, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворовой «Алгебра: 7 класс» / Т. М. Ерина. - М.: Издательство «Экзамен», 2008. - 302, [2] с. (Серия «Учебно-методический комплект»)
8. Звавич Л. И. Алгебра. Дидактические материалы. 7 класс / Л. И. Звавич, Л. В. Кузнецова, С. Б. Суворова. - М.: Просвещение, 2009. - 159 с.: ил.
9. Звавич Л.И. Тестовые задания по геометрии. 7 класс: учебно-методическое пособие/ Л.И. Звавич, Е.В. Потоскуев. - Дрофа, 2006. - 253, [3] с.: ил.
-
Макарычев Ю.Н., Миндюк Н.Г. и др. Алгебра: Учеб. для 7 кл. общеобразоват. учреждений / под ред. С.А. Теляковского. М.: Просвещение, 2008-2009.
-
school-collection.edu.ru/ - единая коллекция цифровых образовательных ресурсов.
Источники информации для учащихся
-
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия, 7-9: учеб. для общеобразоват. учреждений - М. : Просвещение, 2009. - 384 с. : ил.
-
Зив Б.Г., Мейлер В.М. Дидактические материалы по геометрии для 7 класса. - 7-е изд. - М. : Просвещение, 2007. - 128 с. : ил.
-
Звавич Л. И. Алгебра. Дидактические материалы. 7 класс / Л. И. Звавич, Л. В. Кузнецова, С. Б. Суворова. - М.: Просвещение, 2009. - 159 с.: ил.
-
Макарычев Ю.Н., Миндюк Н.Г. и др. Алгебра: Учеб. для 7 кл. общеобразоват. учреждений / под ред. С.А. Теляковского. М.: Просвещение, 2013.
</

-