- Учителю
- Рабочая учебная программа по алгебре 7 класс Ю. Н. Макарычев
Рабочая учебная программа по алгебре 7 класс Ю. Н. Макарычев
АЛГЕБРА 7 КЛАСС
Алгебра: Учеб. для 7 кл. общеобразоват. учреждений / Ю. Н, Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского, 2006г
Пояснительная записка к рабочей учебной программе
Рабочая программа по алгебре составлена в соответствии с требованиями федерального компонента государственного стандарта основного общего образования.
Данная рабочая программа ориентирована на учащихся 7 классов и реализуется на основе следующих документов:
1. Программа для общеобразовательных школ, гимназий, лицеев:
Сборник "Программы для общеобразовательных школ, гимназий, лицеев: Математика. 5-11 кл."/ Сост. Г.М.Кузнецова, Н.Г. Миндюк. - 3-е изд., стереотип.- М. Дрофа, 2002; 4-е изд. - 2004г.
2. Стандарт основного общего образования по математике.
Стандарт основного общего образования по математике //Математика в школе. - 2004г,-№4, -с.4
Данный учебный предмет имеет своей целью:
-
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
-
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;
-
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
-
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.
Основные развивающие и воспитательные цели
Развитие:
-
Ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
-
Математической речи;
-
Сенсорной сферы; двигательной моторики;
-
Внимания; памяти;
-
Навыков само и взаимопроверки.
Формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов.
Воспитание:
-
Культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса;
-
Волевых качеств;
-
Коммуникабельности;
-
Ответственности.
Изучение математики на ступени основного общего образования способствует решению следующих задач:
-
повторить и закрепить знания, умения и навыки полученные в 5-6 классах: вычислительные навыки, умения решать линейные уравнения и неравенства, их системы, умения строить графики функций и др.
-
изучить квадратичную функцию и её график, решение квадратных неравенств графическим методом и методом интервалов;
-
научить решать уравнения и их системы разными способами;
-
изучить арифметическую и геометрическую прогрессии, научить решать задачи с прогрессиями;
-
ознакомить со степенной функцией, корнем n -ой степени, тригонометрическими функциями любого угла, основными тригонометрическими формулами, элементами теории вероятностей и комбинаторики;
-
качественно подготовиться к выпускным экзаменам.
Место предмета в федеральном базисном учебном плане
Согласно Федеральному базисному учебному плану на изучение математики в 7 классе отводится не менее 170 часов из расчета 5 ч в неделю, из школьного компонента выделен еще 1 час в неделю, итого 4 недельных часа или 136 часов в год.
В настоящей рабочей программе внесены изменения: увеличено количество часов на изучение тем, добавлены темы элементов статистики (подробнее расписано в Содержании тем учебного курса). Для более широкого знакомства с математикой введен курс «Элементы статистики и теории вероятностей» в количестве 5 часов. На этом этапе продолжается решение задач путем перебора возможных вариантов, изучается статистический подход к понятию вероятности. Дается классическое определение вероятности, формируются умения вычислять вероятности с помощью формул комбинаторики. Особое внимание уделяется правилу сложения вероятностей.
Внесение данных изменений позволит охватить весь изучаемый материал по программе, повысить уровень обученности учащихся по предмету, а также более эффективно осуществить индивидуальный подход к обучающимся.
Личностные, метапредметные и предметные результаты освоения учебного
предмета «Математика»
Личностными результатами изучения предмета «Математика» (в виде следующих учебных курсов 7 класс - «Математика» («Алгебра» и «Геометрия») являются следующие качества:
- независимость и критичность мышления;
- воля и настойчивость в достижении цели.
Средством достижения этих результатов является:
- система заданий учебников;
- представленная в учебниках в явном виде организация материала по принципу минимакса;
- использование совокупности технологий, ориентированных на развитие самостоятельности и критичности мышления: технология системно- деятельностного подхода в обучении, технология оценивания.
Метапредметными результатами изучения курса «Математика» является формирование универсальных учебных действий (УУД).
Регулятивные УУД:
- самостоятельно обнаруживать и формулировать проблему в классной и индивидуальной учебной деятельности;
- выдвигать версии решения проблемы, осознавать конечный результат, выбирать средства достижения цели из предложенных или их искать самостоятельно;
- составлять (индивидуально или в группе) план решения проблемы (выполнения проекта);
- подбирать к каждой проблеме (задаче) адекватную ей теоретическую модель;
- работая по предложенному или самостоятельно составленному плану, использовать наряду с основными и дополнительные средства (справочная литература, сложные приборы, компьютер);
- планировать свою индивидуальную образовательную траекторию;
- работать по самостоятельно составленному плану, сверяясь с ним и с целью деятельности, исправляя ошибки, используя самостоятельно подобранные средства (в том числе и Интернет);
- свободно пользоваться выработанными критериями оценки и самооценки, исходя из цели и имеющихся критериев, различая результат и способы действий;
- в ходе представления проекта давать оценку его результатам;
- самостоятельно осознавать причины своего успеха или неуспеха и находить способы выхода из ситуации неуспеха;
- уметь оценить степень успешности своей индивидуальной образовательной деятельности;
- давать оценку своим личностным качествам и чертам характера («каков я»), определять направления своего развития («каким я хочу стать», «что мне для этого надо сделать»).
Средством формирования регулятивных УУД служат технология системно- деятельностного подхода на этапе изучения нового материала и технология оценивания образовательных достижений (учебных успехов).
Познавательные УУД:
- анализировать, сравнивать, классифицировать и обобщать факты и явления;
- осуществлять сравнение, сериацию и классификацию, самостоятельно выбирая основания и критерии для указанных логических операций; строить классификацию путём дихотомического деления (на основе отрицания);
- строить логически обоснованное рассуждение, включающее установление причинно-следственных связей;
- создавать математические модели;
- составлять тезисы, различные виды планов (простых, сложных и т.п.). Преобразовывать информацию из одного вида в другой (таблицу в текст, диаграмму и пр.);
- вычитывать все уровни текстовой информации.
- уметь определять возможные источники необходимых сведений, производить поиск информации, анализировать и оценивать её достоверность.
- понимая позицию другого человека, различать в его речи: мнение (точку зрения), доказательство (аргументы), факты; гипотезы, аксиомы, теории. Для этого самостоятельно использовать различные виды чтения (изучающее, просмотровое, ознакомительное, поисковое), приёмы слушания.
- самому создавать источники информации разного типа и для разных аудиторий, соблюдать информационную гигиену и правила информационной безопасности;
- уметь использовать компьютерные и коммуникационные технологии как инструмент для достижения своих целей. Уметь выбирать адекватные задаче инструментальные программно-аппаратные средства и сервисы.
Средством формирования познавательных УУД служат учебный материал и прежде всего продуктивные задания учебника.
- Использование математических знаний для решения различных математических задач и оценки полученных результатов.
- Совокупность умений по использованию доказательной математической речи.
- Совокупность умений по работе с информацией, в том числе и с различными математическими текстами.
- Умения использовать математические средства для изучения и описания реальных процессов и явлений.
- Независимость и критичность мышления.
- Воля и настойчивость в достижении цели.
Коммуникативные УУД:
- самостоятельно организовывать учебное взаимодействие в группе (определять общие цели, договариваться друг с другом и т.д.);
- отстаивая свою точку зрения, приводить аргументы, подтверждая их фактами;
- в дискуссии уметь выдвинуть контраргументы;
- учиться критично относиться к своему мнению, с достоинством признавать ошибочность своего мнения (если оно таково) и корректировать его;
- понимая позицию другого, различать в его речи: мнение (точку зрения), доказательство (аргументы), факты; гипотезы, аксиомы, теории;
- уметь взглянуть на ситуацию с иной позиции и договариваться с людьми иных позиций.
Средством формирования коммуникативных УУД служат технология проблемного обучения, организация работы в малых группах, также использование на уроках технологии личностно- ориентированного и системно- деятельностного обучения.
Требования к уровню подготовки
В результате изучения курса алгебры 7 класса учащиеся должны:
Знать
-
какие числа являются целыми, дробными, рациональными, положительными, отрицательными и др.; свойства действий над числами; знать и понимать термины «числовое выражение», «выражение с переменными», «значение выражения», тождество, «тождественные преобразования».
-
что называется линейным уравнением с одной переменной, что значит решить уравнение, что такое корни уравнения.
-
определения функции, области определения функции, области значений, что такое аргумент, какая переменная называется зависимой, какая независимой; понимать, что функция - это математическая модель, позволяющая описывать и изучать разнообразные зависимости между реальными величинами, что конкретные типы функций (прямая и обратная пропорциональности, линейная) описывают большое разнообразие реальных зависимостей.
-
определение степени, одночлена, многочлена; свойства степени с натуральным показателем, свойства функций у=х2, у=х3.
-
определения абсолютной и относительной погрешностей;
-
определение многочлена, понимать формулировку заданий: «упростить выражение», «разложить на множители».
-
формулы сокращенного умножения: квадратов суммы и разности двух выражений.
-
различные способы разложения многочленов на множители.
-
, что такое линейное уравнение с двумя переменными, система уравнений,
-
различные способы решения систем уравнений с двумя переменными: способ подстановки, способ сложения;
Уметь
-
осуществлять в буквенных выражениях числовые подстановки и выполнять соответствующие вычисления; сравнивать значения буквенных выражений при заданных значениях входящих в них переменных; применять свойства действий над числами при нахождении значений числовых выражений.
-
применять изученную теорию при тождественных преобразованиях выражений.
-
решать линейные уравнения с одной переменной, а также сводящиеся к ним; правильно употреблять термины «уравнение», «корень уравнения», понимать их в тексте и в речи учителя, понимать формулировку задачи «решить уравнение»»; решать текстовые задачи с помощью составления линейных уравнений с одной переменной.
-
применять изученную теорию при решении уравнений с одной переменной, решать задачи с помощью уравнений.
-
правильно употреблять функциональную терминологию (значение функции, аргумент, график функции, область определение, область значений), понимать ее в тексте, в речи учителя, в формулировке задач; находить значения функций, заданных формулой, таблицей, графиком; решать обратную задачу; строить графики линейной функции, прямой и обратной пропорциональности; интерпретировать в несложных случаях графики реальных зависимостей между
-
применять изученную теорию при выполнении письменных заданий, строить графики.
-
находить значения функций, заданных формулой, таблицей, графиком; решать обратную задачу; строить графики функций у=х2, у=х3;
-
выполнять действия со степенями с натуральным показателем; преобразовывать выражения, содержащие степени с натуральным показателем; приводить одночлен к стандартному виду.
-
применять изученную теорию при построение графиков функций у=х2, у=х3, упрощать выражения, содержащие степени с натуральным показателем.
-
приводить многочлен к стандартному виду, выполнять действия с одночленом и многочленом; выполнять разложение многочлена вынесением общего множителя за скобки.
-
умножать многочлен на многочлен, раскладывать многочлен на множители способом группировки, доказывать тождества.
-
читать формулы сокращенного умножения, выполнять преобразование выражений применением формул сокращенного умножения: квадрата суммы и разности двух выражение, умножения разности двух выражений на их сумму; выполнять разложение разности квадратов двух выражений на множители.
-
применять различные способы разложения многочленов на множители; преобразовывать целые выражения; применять преобразование целых выражений при решении задач.
-
применять изученную теорию при выполнении письменных заданий по данной теме.
-
правильно употреблять термины: «уравнение с двумя переменными», «система»; понимать их в тексте, в речи учителя, понимать формулировку задачи «решить систему уравнений с двумя переменными»; строить некоторые графики уравнения с двумя переменными; решать системы уравнений с двумя переменными различными способами.
-
применять приобретенные знания, умения и навыки при выполнении письменных заданий.
Общеучебные умения, навыки и способы деятельности.
В ходе преподавания математики в основной школе, работы над формированием у учащихся перечисленных в программе знаний и умений, следует обращать внимание на то, чтобы они овладевали умениями общеучебного характера, разнообразными способами деятельности, приобретали опыт:
планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых алгоритмов;
решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;
исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;
ясного, точного, грамотного изложения своих мыслей в устной и письменной речи, использования различных языков математики (словесного, символического, графического), свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства;
проведения доказательных рассуждений, аргументации, выдвижения гипотез и их обоснования;
поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.
Результаты обучения
Результаты обучения представлены в Требованиях к уровню подготовки и задают систему итоговых результатов обучения, которых должны достигать все учащиеся, оканчивающие основную школу, и достижение которых является обязательным условием положительной аттестации ученика за курс основной школы. Эти требования структурированы по трем компонентам: «знать/понимать», «уметь», «использовать приобретенные знания и умения в практической деятельности и повседневной жизни
Учебно - тематический план
№
главы
Тема
Количество
часов
Контрольные работы
I
Выражения, тождества, уравнения
31
2
II
Функции
15
1
III
Степень с натуральным показателем
18
1
IV
Многочлены
20
2
V
Формулы сокращенного умножения
25
2
VI
Системы линейных уравнений
17
1
Повторение
10
1
Всего
136
10
Содержание тем учебного курса.
1. Выражения и их преобразования. Уравнения. Статистические характеристики. (31 ч)
Числовые выражения и выражения с переменными. Простейшие преобразования выражений. Уравнение с одним неизвестным и его корень, линейное уравнение. Решение задач методом уравнений. Среднее арифметическое, размах, мода. Медиана как статистическая характеристика. формулы
Цель - систематизировать и обобщить сведения о преобразовании выражений и решении уравнений с одним неизвестным, полученные учащимися в курсе математики 5,6 классов.
Знать какие числа являются целыми, дробными, рациональными, положительными, отрицательными и др.; свойства действий над числами; знать и понимать термины «числовое выражение», «выражение с переменными», «значение выражения», тождество, «тождественные преобразования».
Уметь осуществлять в буквенных выражениях числовые подстановки и выполнять соответствующие вычисления; сравнивать значения буквенных выражений при заданных значениях входящих в них переменных; применять свойства действий над числами при нахождении значений числовых выражений.
2. Функции (15 ч)
Функция, область определения функции, Способы задания функции. График функции. Функция y=kx+b и её график. Функция y=kx и её график.
Цель - познакомить учащихся с основными функциональными понятиями и с графиками функций y=kx+b, y=kx.
Знать определения функции, области определения функции, области значений, что такое аргумент, какая переменная называется зависимой, какая независимой; понимать, что функция - это математическая модель, позволяющая описывать и изучать разнообразные зависимости между реальными величинами, что конкретные типы функций (прямая и обратная пропорциональности, линейная) описывают большое разнообразие реальных зависимостей.
Уметь правильно употреблять функциональную терминологию (значение функции, аргумент, график функции, область определение, область значений), понимать ее в тексте, в речи учителя, в формулировке задач; находить значения функций, заданных формулой, таблицей, графиком; решать обратную задачу; строить графики линейной функции, прямой и обратной пропорциональности; интерпретировать в несложных случаях графики реальных зависимостей между величинами, отвечая на поставленные вопросы
3. Степень с натуральным показателем ( 18 ч)
Степень с натуральным показателем и её свойства. Одночлен. Функции y=x2, y=x3, и их графики.
Цель - выработать умение выполнять действия над степенями с натуральными показателями.
Знать определение степени, одночлена, многочлена; свойства степени с натуральным показателем, свойства функций у=х2, у=х3.
Уметь находить значения функций, заданных формулой, таблицей, графиком; решать обратную задачу; строить графики функций у=х2, у=х3; выполнять действия со степенями с натуральным показателем; преобразовывать выражения, содержащие степени с натуральным показателем; приводить одночлен к стандартному виду.
4. Многочлены (20 ч)
Многочлен. Сложение, вычитание и умножение многочленов. Разложение многочлена на множители.
Цель - выработать умение выполнять сложение, вычитание, умножение многочленов и разложение многочленов на множители.
Знать определение многочлена, понимать формулировку заданий: «упростить выражение», «разложить на множители».
Уметь приводить многочлен к стандартному виду, выполнять действия с одночленом и многочленом; выполнять разложение многочлена вынесением общего множителя за скобки; умножать многочлен на многочлен, раскладывать многочлен на множители способом группировки, доказывать тождества.
5. Формулы сокращённого умножения (25 ч)
Формулы ![]() . Применение формул сокращённого умножения к разложению на множители.
. Применение формул сокращённого умножения к разложению на множители.
Цель - выработать умение применять в несложных случаях формулы сокращённого умножения для преобразования целых выражений в многочлены и для разложения многочленов на множители.
Знать формулы сокращенного умножения: квадратов суммы и разности двух выражений; различные способы разложения многочленов на множители.
Уметь читать формулы сокращенного умножения, выполнять преобразование выражений применением формул сокращенного умножения: квадрата суммы и разности двух выражение, умножения разности двух выражений на их сумму; выполнять разложение разности квадратов двух выражений на множители; применять различные способы разложения многочленов на множители; преобразовывать целые выражения; применять преобразование целых выражений при решении задач.
6. Системы линейных уравнений (17 ч)
Система уравнений с двумя переменными. Решение систем двух линейных уравнений с двумя переменными. Решение задач методом составления систем уравнений..
Цель - познакомить учащихся со способами решения систем линейных уравнений с двумя переменными, выработать умение решать системы уравнений и прменять их при решении текстовых задач.
Знать, что такое линейное уравнение с двумя переменными, система уравнений, знать различные способы решения систем уравнений с двумя переменными: способ подстановки, способ сложения; понимать, что уравнение - это математический аппарат решения разнообразных задач из математики, смежных областей знаний, практики.
Уметь правильно употреблять термины: «уравнение с двумя переменными», «система»; понимать их в тексте, в речи учителя, понимать формулировку задачи «решить систему уравнений с двумя переменными»; строить некоторые графики уравнения с двумя переменными; решать системы уравнений с двумя переменными различными способами.
7. Повторение. Решение задач ( 10 ч)
Закрепление знаний, умений и навыков, полученных на уроках по данным темам (курс алгебры 7 класса).
Контроль уровня обученности
Текущий и промежуточный контроль осуществляется в ходе занятий при написании контрольных работ, самостоятельных работ, математических диктантов и тестирования. Итоговый контроль осуществляется в конце учебного года в виде итоговой контрольной работы или в виде теста (см приложение).
Литература и средства обучения
-
Алгебра: Учеб. для 7 кл. общеобразоват. учреждений / Ю. Н, Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского. - 15-е изд., дораб - М.: Просвещение, 2008. - 272 с.: ил.
-
Уроки алгебры в 7 классе. / В.И. Жохов, Л.Б. Крайнева. Пособие для учителей. / М.: Вербум - М, 2000. - 96 с.
-
Дидактические материалы по алгебре.7 класс. / Ю.Н. Макарычев, Н.Г. Миндюк, Л.М. Короткова. / М: Просвещение, 1997 - 160с.
-
Разноуровневые дидактические материалы по алгебре. 7 класс. / Н.Г. Миндюк, М.Б. Миндюк. / М.: Генжер, 1999. - 95 с.
-
-
Математика в таблицах. 5-11 классы. Справочные материалы.-Москва «АСТ.
-
Астрель» 2004
-
-
6. . Дидактические материалы по алгебре для 7 класса. Л.И. Звавич, Л.В. Кузнецова, С.Б. Суворова-Москва «Просвещение» 2001
-
7. Контрольные и зачетные работы по алгебре. 7 класс. П.И. Алтынов-Москва «Экзамен»
-
2007
-
Тесты по алгебре. 7 класс. П.И. Алтынов-Москва «Экзамен» 2008
-
Контрольные и проверочные работы по алгебре. 7 класс. Л.И. Звавич, Л.Я. Шляпочник,
-
Б.В. Козулин-Москва «Дрофа» 2005
Программы для общеобразовательных школ, гимназий, лицеев: Математика, 5 - 11 кл. / Сост. Г.М. Кузнецова, Н.Г. Миндюк. / 4-е изд., стереотип. М.: Дрофа, 2004. - 320 с -
-
Программы общеобразовательных учреждений Алгебра 7 - 9 классы. М:- Просвещение 2008 г..
Образовательные диски.
-
Математика 5 - 11 классы. Практикум. Под редакцией Дубровского. НФПК 2004 год.
-
Алгебра 7 - 9 классы. Дидактический и раздаточный материал. Под редакцией Афанасьевой Т. Л. Изд. «Учитель». 2009.
-
Математика 5 - 11 классы. Практикум. Дрофа. 2004.
-
Электронный учебник - справочник Алгебра 7 - 11 класс. ЗАО «Кудиц» 2000 г.
-
«Живая школа» Живая геометрия. Виртуальная лаборатория. Институт новых технологических образований.
-
Уроки алгебры Кирилла и Мефодия. 7 - 8 классы. Виртуальная школа Кирилла и Мефодия. ООО «Кирилл и Мефодий» 2004г
Интернет - ресурсы:
-
Министерство образования РФ: ;
-
Тестирование online: 5 - 11 классы:
-
Педагогическая Сеть «Методисты.ру»
-
Новые технологии в образовании:
-
Путеводитель «В мире науки» для школьников:
-
Мегаэнциклопедия Кирилла и Мефодия:
-
сайты «Энциклопедий»: ;
-
сайт для самообразования и он-лайн тестирования:
-
досье школьного учителя математики:
-
ПРИЛОЖЕНИЕ
Итоговая контрольная работа.
Вариант 1.
• 1. Упростите выражение:
а) 3а2b ∙ (-5а3b); б) (2х2у)3.
• 2. Решите уравнение:
3х - 5(2х + 1) = 3(3 - 2х).
• 3. Разложите на множители: а) 2ху - 6у2; б) а3 - 4а.
• 4. Периметр треугольника АВС равен 50 см. Сторона АВ на 2 см больше стороны ВС, а сторона АС в2 раза больше стороны ВС. Найдите стороны треугольника.
5. Докажите, что верно равенство:
(а + с) (а - с) - b(2а - b) - (a - b + c) (a - b - c) = 0.
6. На графике функции у = 5х - 8 найдите точку, абсцисса которой противоположна её ординате.
Вариант 2.
• 1. Упростите выражение:
а) -2ху2 ∙ 3х3у5; б) (-4аb3)2.
• 2. Решите уравнение:
4(1 - 5х) = 9 - 3(6х - 5).
• 3. Разложите на множители: а) а2b - ab2; б) 9х - х3.
• 4. Турист прошёл 50 км за 3 дня. Во второй день он прошёл на 10 км меньше, чем в первый день, и на 5 км больше, чем в третий. Сколько километров проходил турист каждый день?
5. Докажите, что при любых значениях переменных верно равенство:
(х - у)(х + у) - (а - х + у)(а - х - у) - а(2х - а) = 0.
6. На графике функции у = 3х + 8 найдите точку, абсцисса которой равна её ординате.
Итоговый тест за курс 7 класса.
Вариант 1.
1. Найдите значение выражения ![]() если а = 0,25.
если а = 0,25.
Ответ:______________.
2. Товар стоил 3200 р. Сколько стал стоить этот товар после снижения цены на 5%?
А. 3040 р. Б. 304 р. В. 1600 р. Г. 3100 р.
3. Учащиеся класса в среднем выполнили по 7,5 заданий из предложенного теста. Максим выполнил 9 заданий. На сколько процентов его результат выше среднего?
Ответ:______________.
4. Ряд состоит из натуральных чисел. Какая из следующих статистических характеристик не может выражаться дробным числом?
А. Среднее арифметическое Б. Мода В. Медиана
Г. Такой характеристики среди данных нет
5. Какое из уравнений не имеет корней?
А. ![]() Б.
Б. ![]() В.
В. ![]() Г.
Г. ![]()
![]()
6. На координатной прямой отмечены числа А и В (рис. 1).
Сравните числа -А и В.




А 0 В
Рис. 1
А. -А < В Б. -А > В В. -А = В
Г. Сравнить невозможно.
7. Упростите выражение: а(а - 2) - (а - 1)(а + 1).
Ответ:_________________.
8. Значения каких переменных надо знать, чтобы найти значение выражения
(5а - 2b)(5a + 2b) - 4b(3a - b) + 6a(2b - 1)?
А. а и b Б. а В. b
Г. Значение выражения не зависит от значений переменных.
9. Решите уравнение:
(х - 2)2 + 8х = (х - 1)(1 + х).
Ответ:________________.
10. Решите систему уравнений: 
Ответ:________________.
11. За 3 ч езды на автомобиле и 4 ч езды на поезде туристы проехали 620 км, причём скорость поезда была на 10 км/ч больше скорости автомобиля?
Обозначив через х км/ч скорость автомобиля и через у км/ч скорость поезда, составили системы уравнений. Какая из них составлена правильно?
А. 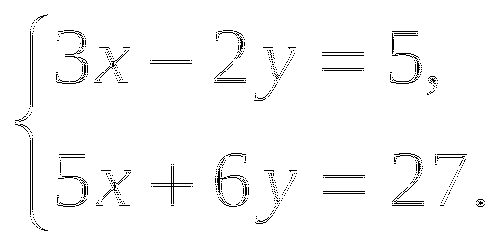 Б.
Б. 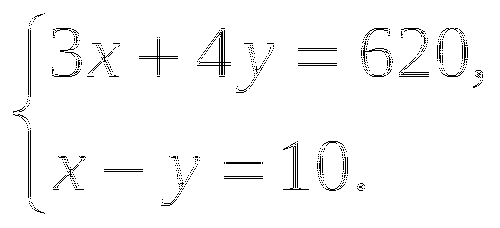
В. 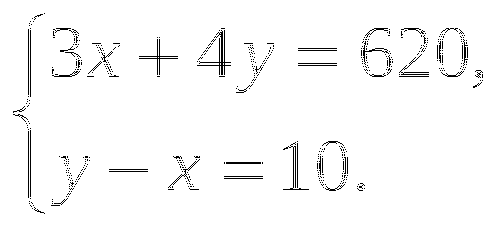 Г.
Г. 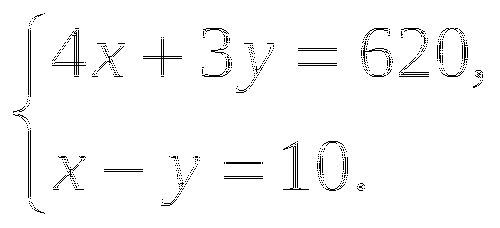
12. Какая из точек не принадлежит графику функции у = -0,6х + 1?
А. (3; -0,8) Б. (-3; 0,8) В. (2; -0,2) Г. (-2; 2,2)
13. В какой координатной четверти нет ни одной точки графика функции
у = -0,6х + 1,5?
Ответ:________________.
14. Задайте формулой линейную функцию, график которой пересекает ось х в точке (2; 0) и ось у в точке (0; 7).
Ответ:________________.
Вариант 2.
1. Найдите значение выражения ![]() если х = 2,25.
если х = 2,25.
Ответ:______________.
2. Товар стоил 1600 р. Сколько стал стоить этот товар после повышения цены на 5%?
А. 1760 р. Б. 1700 р. В. 1605 р. Г. 1680 р.
3. За смену токари цеха обработали в среднем по 12,5 деталей. Петров обработал за эту смену 15 деталей. На сколько процентов его результат выше среднего?
Ответ:______________.
4. В ряду данных все числа целые. Какая из следующих характеристик не может выражаться дробным числом?
А. Среднее арифметическое Б. Мода В. Медиана
Г. Такой характеристики среди данных нет
5. Какое из уравнений не имеет корней?
А. ![]() Б.
Б. ![]() В.
В. ![]() Г.
Г. ![]()
![]()
6. На координатной прямой отмечены числа В и С (рис. 2).
Сравните числа В и -С.




С 0 В
Рис. 2
А. В > -С Б. В < -С В. В = -С
Г. Сравнить невозможно.
7. Упростите выражение: х(х - 6) - (х - 2)(х + 2).
Ответ:________________.
8. Значения каких переменных надо знать, чтобы найти значение выражения
(3х - 4у)(3х + 4у) - 3х(3х - у) + 3у(1 - х)?
А. х Б. у В. х и у
Г. Значение выражения не зависит от значений переменных.
9. Решите уравнение:
(х + 3)2 - х = (х - 2)(2 + х).
Ответ:________________.
10. Решите систему уравнений: 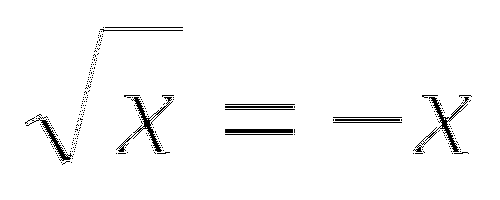
Ответ:________________.
11. Масса 5 см3 железа и 10 см3 меди равна 122 г. Масса 4 см3 железа больше массы 2 см3 меди на 14,6 г. Каковы плотность железа и плотность меди?
Обозначив через х г/см3 плотность железа и через у г/см3 плотность меди, составили системы уравнений. Какая из них составлена правильно?
А.  Б.
Б. 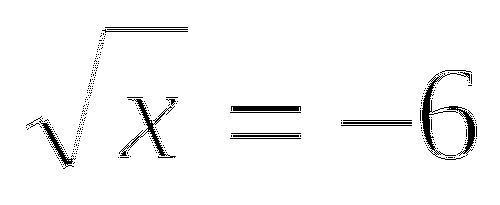
В.  Г.
Г. 
12. Какая из точек не принадлежит графику функции у = -1,2х - 1,4?
А. (-1; -0,2) Б. (-2; -1) В. (0; -1,4) Г. (-3; 2,2)
13. В какой координатной четверти нет ни одной точки графика функции
у = 1,8х - 7,2?
Ответ:________________.
14. Задайте формулой линейную функцию, график которой пересекает ось х в точке (-4; 0) и ось у в точке (0; 3).
Ответ:________________.
![]()