- Учителю
- Практическое пособие по математике для 7-9 классов «Основные алгоритмы алгебры»
Практическое пособие по математике для 7-9 классов «Основные алгоритмы алгебры»
Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа №32 г. Новочеркасска
Принято
методическим объединением учителей
математики и методическим советом
протокол №1 от «30» августа 2012 года
«Утверждаю»
Директор школы Салтыков С.А.
«31» августа 2012года
Основные алгоритмы алгебры
7 - 9 классов
Учитель Кручинина В.Б.
Алгоритм решения линейных уравнений
Уравнение вида ![]() , где a,b действительные числа, называется линейным.
, где a,b действительные числа, называется линейным.
-
Преобразовать левую и правую части уравнения к виду
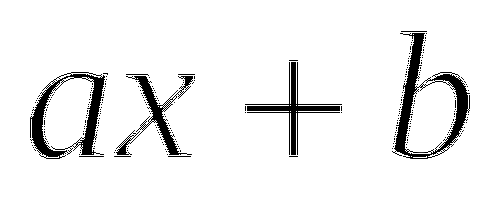 , для этого нужно раскрыть скобки (если они есть) или привести дробные слагаемые к общему знаменателю (если нужно).
, для этого нужно раскрыть скобки (если они есть) или привести дробные слагаемые к общему знаменателю (если нужно). -
Перенести все члены, содержащие неизвестную, влево, а все известные члены - вправо (при переносе членов из одной части в другую изменяем их знак на противоположный).
-
Приводим подобные члены в левой и правой частях уравнения.
-
Число, стоящее справа, делим на число, стоящее перед неизвестной.
-
Записываем ответ (результат деления - корень исходного уравнения).
Пример
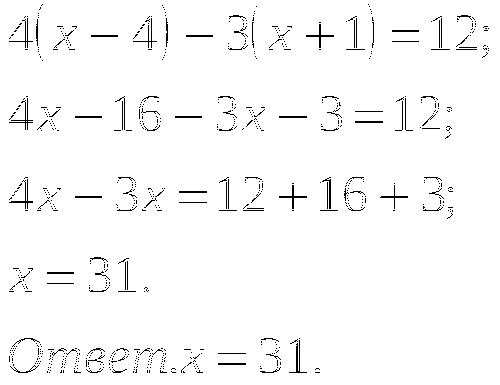
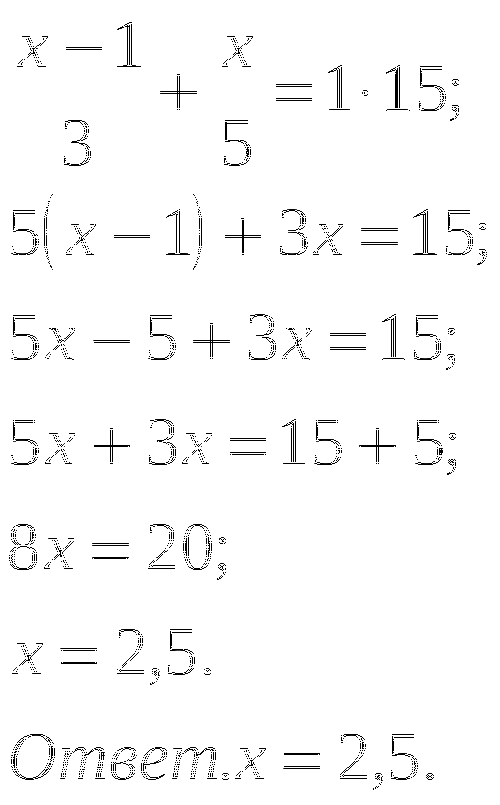
Решить самостоятельно
Алгоритм решения линейных неравенств
Неравенство вида ![]() , где a,b действительные числа, называется линейным.
, где a,b действительные числа, называется линейным.
-
Преобразовать левую и правую части неравенства к виду
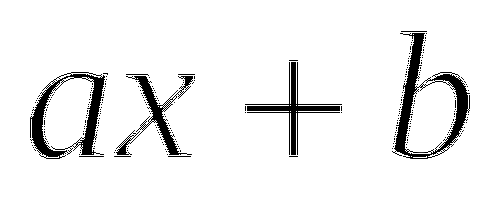 , для этого нужно раскрыть скобки (если они есть) или привести дробные слагаемые к общему знаменателю (если нужно).
, для этого нужно раскрыть скобки (если они есть) или привести дробные слагаемые к общему знаменателю (если нужно). -
Перенести все члены, содержащие неизвестную, влево, а все известные члены - вправо (при переносе членов из одной части в другую изменяем их знак на противоположный).
-
Приводим подобные члены в левой и правой частях неравенства.
-
Число, стоящее справа, делим на число, стоящее перед неизвестной (при делении на отрицательное число меняем знак неравенства).
-
Записываем ответ в виде неравенства или числового промежутка.
Пример
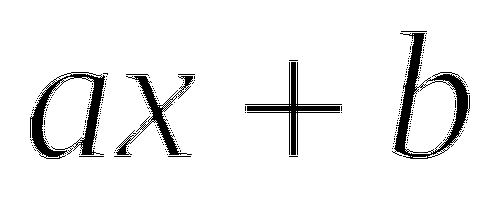
Решить самостоятельно
Алгоритм решения квадратных уравнений
Уравнение вида ![]() , где a,b,c действительные числа,
, где a,b,c действительные числа, ![]() называется квадратным.
называется квадратным.
-
Выпиши значения a,b,c и вычисли дискриминант
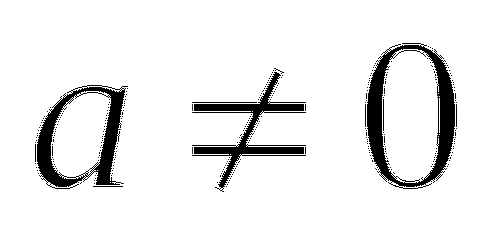 .
. -
Если
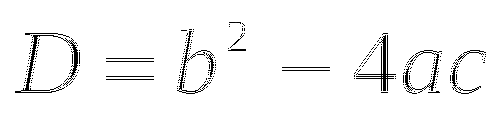 , то находим корни уравнения по формуле
, то находим корни уравнения по формуле  .
. -
Если
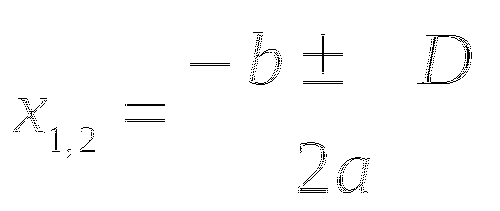 , то находим корни уравнения по формуле
, то находим корни уравнения по формуле 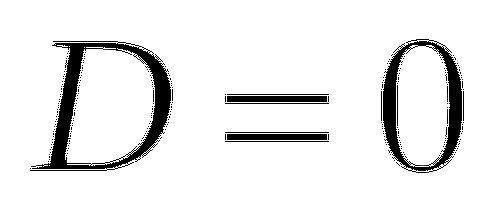 .
. -
Если
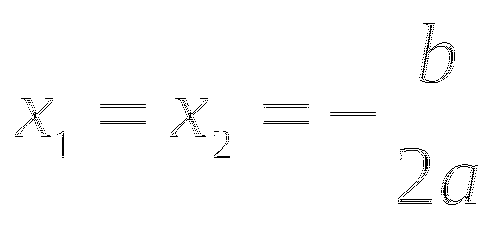 , то уравнение не имеет действительных корней.
, то уравнение не имеет действительных корней. -
Если в уравнении
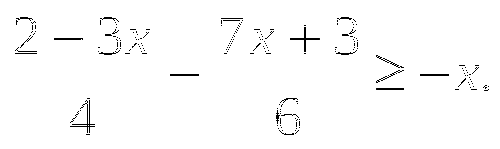 ,
, 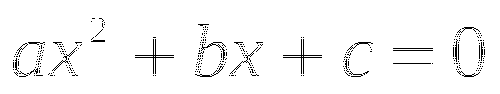 ,
, 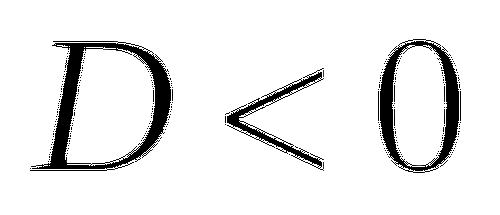 , то получим уравнение:
, то получим уравнение:
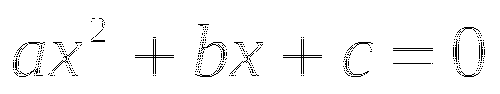
Пример
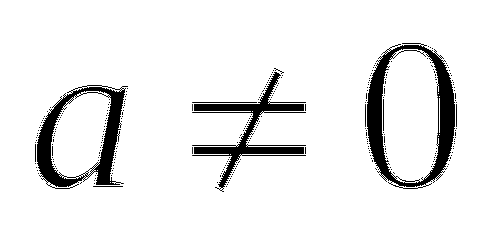
-
Если в уравнении
 ,
, 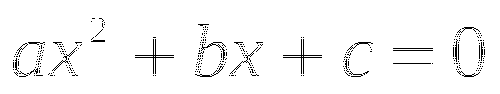 ,
, 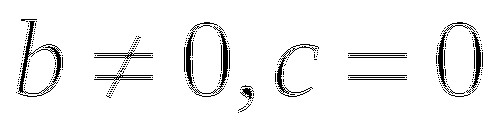 , то получим уравнение:
, то получим уравнение:
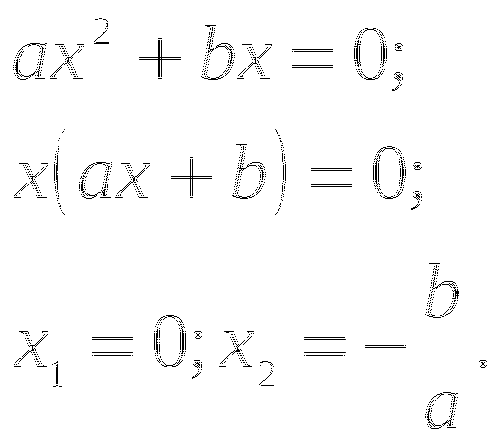
Если ![]() , то нет действительных корней.
, то нет действительных корней.
-
Если в уравнении
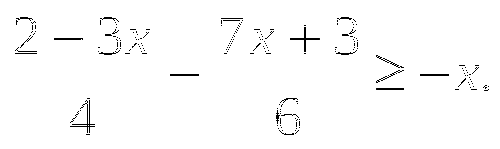 ,
, 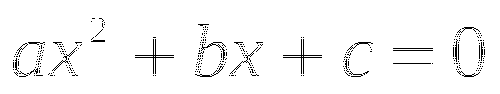 ,
, 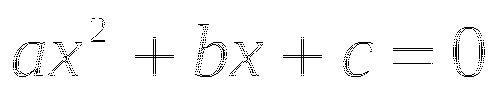 , то получим уравнение:
, то получим уравнение:
![]()
Решить самостоятельно
Алгоритм разложения квадратного трехчлена на множители
-
Реши квадратное уравнение
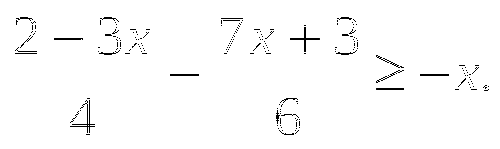 (если корней нет, то нельзя разложить на множители).
(если корней нет, то нельзя разложить на множители). -
Подставь
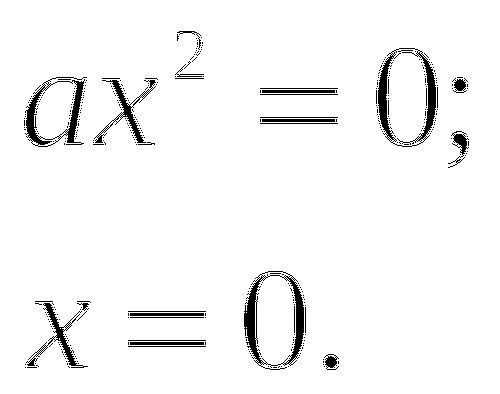 в формулу
в формулу 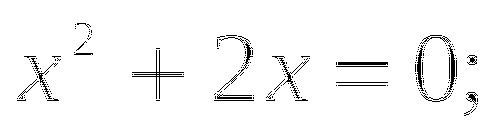
Пример. Разложить на множители ![]() .
.
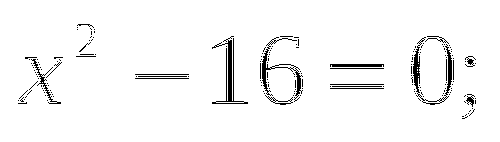
Ответ. ![]()
Решить самостоятельно
Разложить на множители квадратные трехчлены
-
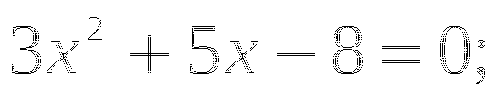 ;
; -
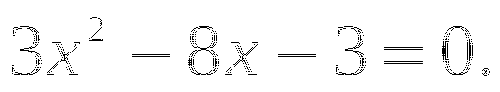 ;
; -
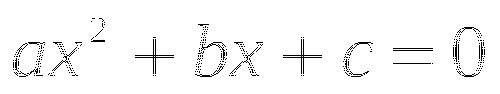 ;
; -
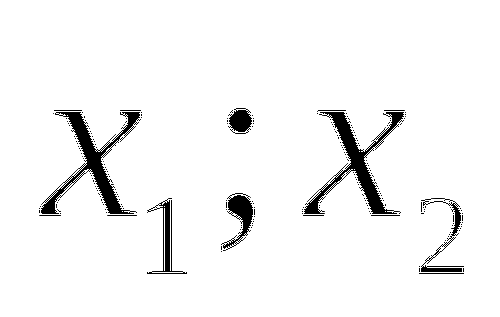 ;
; -
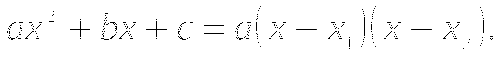 ;
; -
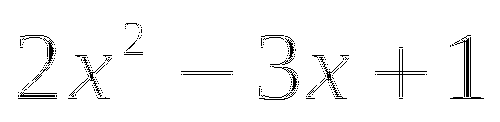 ;
; -
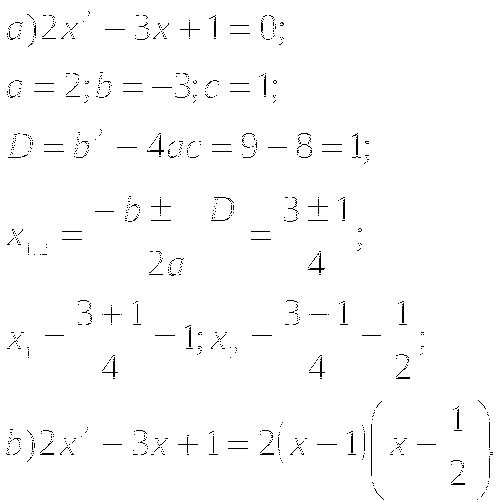 .
.
Сократить дробь
-
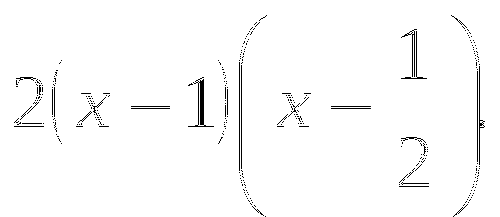 ;
; -
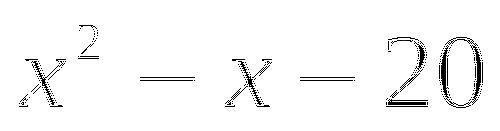 .
.
Алгоритм решения квадратных уравнений
![]() по теореме Виета.
по теореме Виета.
-
Выпиши p, q из уравнения
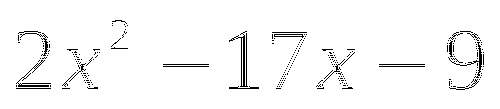 , используя условие, что
, используя условие, что
![]()
-
Подбери пары чисел, которые при умножении дадут число q.
-
Вычисли сумму каждой пары, чтобы получить - p.
Пример
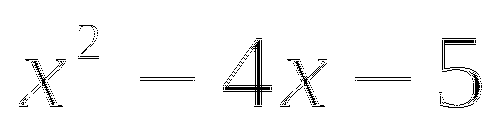
Ответ. ![]()
Решить самостоятельно
Алгоритм построения графика линейной функции
Функция вида ![]() , где
, где ![]() - постоянные, называется линейной.
- постоянные, называется линейной.
![]() - линейная функция, график прямая, не проходит через начало координат (так как
- линейная функция, график прямая, не проходит через начало координат (так как ![]() ), возрастает (если
), возрастает (если ![]() ) и убывает (если
) и убывает (если ![]() ).
).
-
Возьмем любое значение x и подставим его значение в уравнение
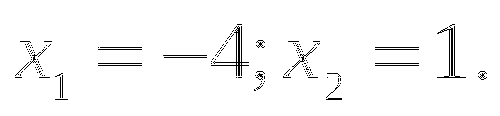 (вместо x). Получим точку с координатами
(вместо x). Получим точку с координатами 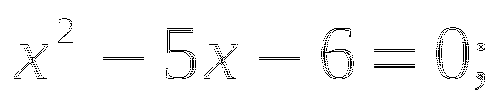 .
. -
Возьмем любое значение x и подставим его значение в уравнение
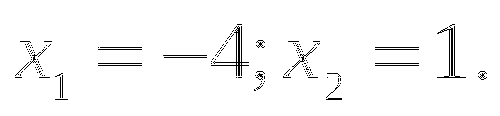 (вместо x). Получим точку с координатами
(вместо x). Получим точку с координатами 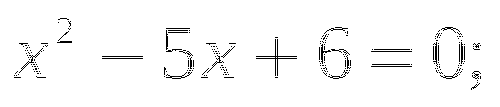 .
. -
Отметим полученные точки на координатной плоскости и проведем через них прямую.
Пример
Постройте график функции ![]() .
.
![]() - линейная функция, график прямая, не проходит через начало координат (так как
- линейная функция, график прямая, не проходит через начало координат (так как ![]() ), возрастает (т.к.
), возрастает (т.к. ![]() ).
).
-
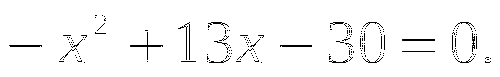 ;
; -
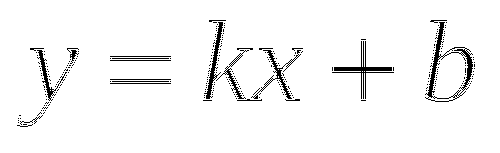 ;
; -
отметим полученные точки на координатной плоскости и проведем через них прямую
Решить самостоятельно
Построить графики данных функций и найти координаты точек пересечения графика с осями координат.
-
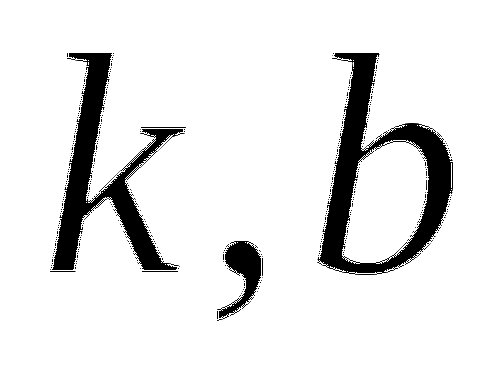 ;
; -
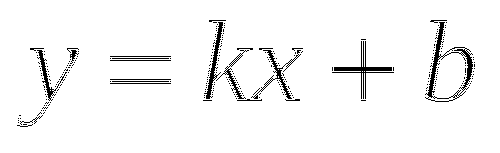 ;
; -
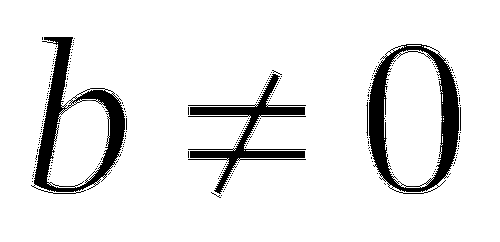 ;
; -
 ;
; -
 .
.
Алгоритм построения графика квадратичной функции
Функция вида ![]() называется квадратичной.
называется квадратичной.
![]() - квадратичная функция, график парабола, ветви которой направлены вверх (если
- квадратичная функция, график парабола, ветви которой направлены вверх (если ![]() ) или вниз (если
) или вниз (если ![]() ).
).
-
Находим координаты вершины параболы
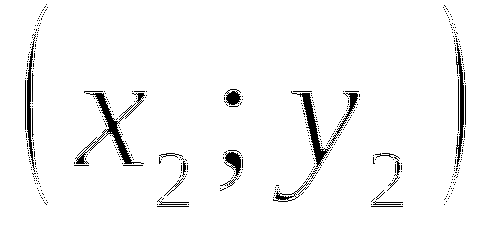 .
. -
Проводим ось симметрии
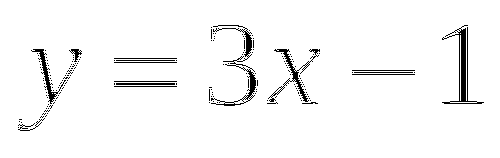 (прямую, параллельную оси Оу, проходящую через вершину параболы).
(прямую, параллельную оси Оу, проходящую через вершину параболы). -
Находим нули функции (абсциссы точек пересечения параболы с осью Ох), для этого решим уравнение
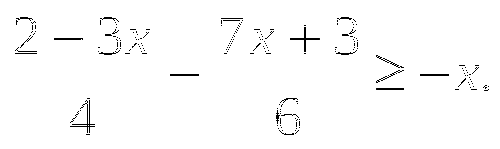 . Если уравнение не имеет действительных корней, то парабола не пересекает ось Ох.
. Если уравнение не имеет действительных корней, то парабола не пересекает ось Ох.
-
Находим дополнительные точки, для этого возьмем любое значение x и подставим его значение в уравнение
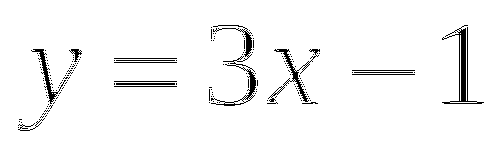 (вместо x). Получим точку с координатами
(вместо x). Получим точку с координатами 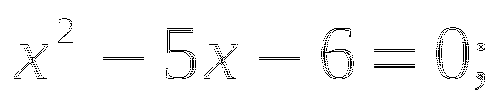 . Возьмем любое значение x и подставим его значение в уравнение
. Возьмем любое значение x и подставим его значение в уравнение 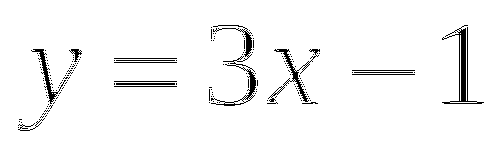 (вместо x). Получим точку с координатами
(вместо x). Получим точку с координатами 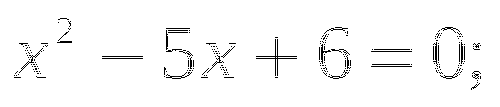 .
. -
Отметим полученные точки на координатной плоскости (точки, симметричные дополнительным точкам). Соединим полученные точки плавной линией и продолжим ветви параболы.
Пример. Построить график функции ![]() .
.
![]() - квадратичная функция, график парабола, ветви которой направлены вверх (если
- квадратичная функция, график парабола, ветви которой направлены вверх (если ![]() ).
).
-
Находим координаты вершины параболы
![]() - вершина параболы.
- вершина параболы.
-
Проводим ось симметрии
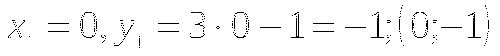 (прямую, параллельную оси Оу, проходящую через вершину параболы).
(прямую, параллельную оси Оу, проходящую через вершину параболы). -
Находим нули функции (абсциссы точек пересечения параболы с осью Ох), для этого решим уравнение
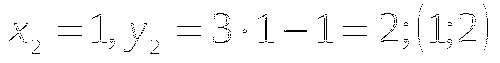 .
. -
Находим дополнительные точки: а)
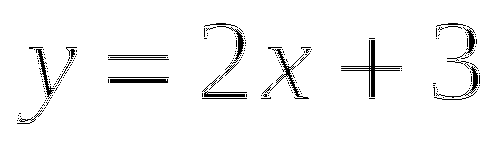 ; б)
; б) 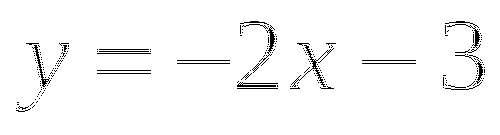 .
. -
Отметим полученные точки на координатной плоскости (точки, симметричные дополнительным точкам). Соединим полученные точки плавной линией и продолжим ветви параболы.
Решить самостоятельно
Построить графики следующих функций:
-
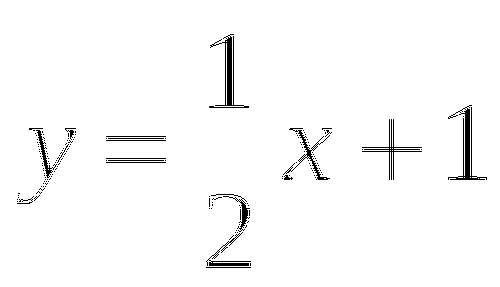 ;
; -
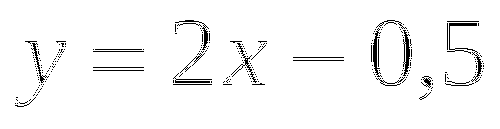 ;
; -
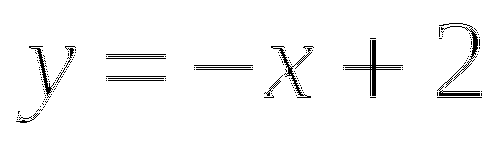 ;
; -
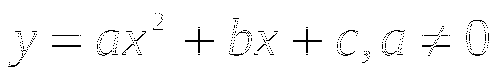 ;
; -
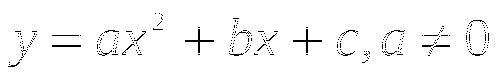 ;
; -
 .
.
Алгоритм построения графика обратно пропорциональной
зависимости
Функция вида ![]() называется обратно пропорциональной зависимостью.
называется обратно пропорциональной зависимостью.
![]() - обратно пропорциональная зависимость, график гипербола, состоит из двух ветвей, расположенных в 1 и 3 четвертях (если
- обратно пропорциональная зависимость, график гипербола, состоит из двух ветвей, расположенных в 1 и 3 четвертях (если ![]() ) и во 2 и 4 четвертях (если
) и во 2 и 4 четвертях (если ![]() ).
).
Убывает при ![]() , если
, если ![]() ; возрастает при
; возрастает при ![]() , если
, если ![]()
-
Возьмем любое положительное значение
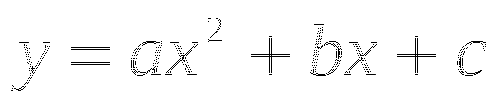 и подставим его значение в формулу
и подставим его значение в формулу 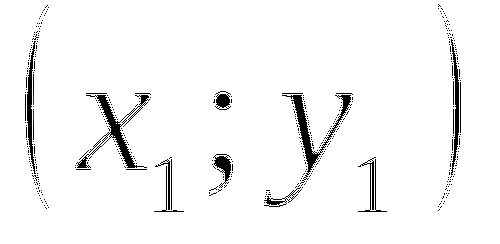 , получим точку
, получим точку 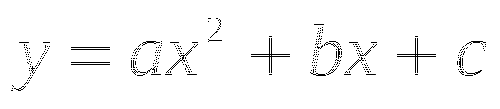 .
. -
Возьмем любое положительное значение
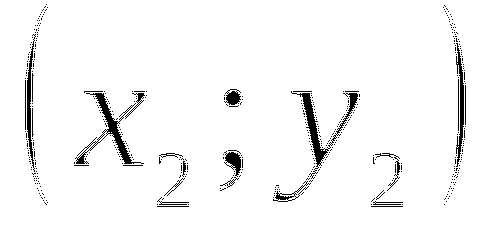 и подставим его значение в формулу
и подставим его значение в формулу 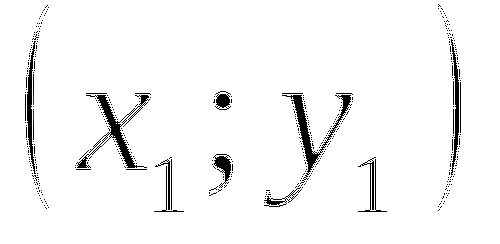 , получим точку
, получим точку 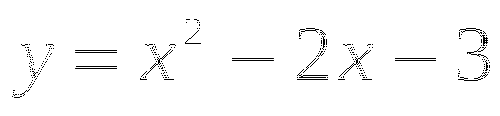 .
. -
Возьмем любое положительное значение
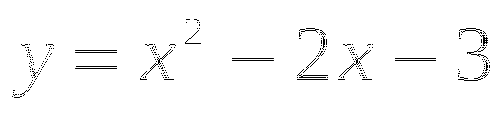 и подставим его значение в формулу
и подставим его значение в формулу 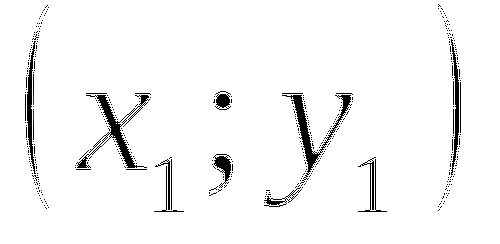 , получим точку
, получим точку  .
. -
При необходимости можно задать еще две точки.
-
Отметим заданные точки и точки, им симметричные, на координатной плоскости. Соединим плавной линией точки в 1 (2) четверти и в 3 (4) четверти.
Пример
Построить график функции ![]() .
.
![]() - обратно пропорциональная зависимость, график гипербола, состоит из двух ветвей, расположенных во 2 и 4 четвертях (
- обратно пропорциональная зависимость, график гипербола, состоит из двух ветвей, расположенных во 2 и 4 четвертях (![]() ), возрастает при
), возрастает при ![]() .
.
-
Область определения функции:
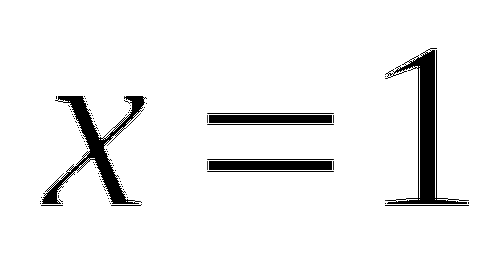 .
. -
Функция нечетная (график симметричен относительно начала координат).
-
Функция возрастает при
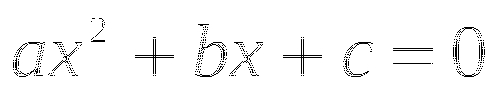 .
. -
Точки: а) (1;-4); б) (2;-2); в) (4;-1).
-
Отметим заданные точки и точки, им симметричные, на координатной плоскости. Соединим плавной линией точки в 2 и в 4 четвертях.
Требования к рабочей тетради
-
Рабочая тетрадь по математике в 5 и 6 классах должна быть 12 листов в клетку с полями, отведенными красной пастой.
-
Все записи должны вестись аккуратно, ручкой с синей пастой.
-
Работа в тетради начинается с записи «Классная работа» или «Домашняя работа», дата записывается на полях, например, 21.09.
-
Указывается тема урока.
-
Записи с доски или под диктовку учителя.
-
Выполнение самостоятельных заданий.
При записи заданий необходимо выполнение следующих требований:
-
Расстояние между работами 4 клетки.
-
Расстояние от полей или от края страницы 1 клетка.
-
Записи ведутся в столбик, с соблюдением размерности, аккуратно, при перечислении ставятся запятые.
-
Задания выделяются номером из учебника или порядковым номером.
-
Выполнение задания начинается со слова «Решение» и заканчивается словом «Ответ».
-
Цифры пишутся в каждой клетке.
-
Исправления нужно выполнять аккуратно, зачеркивая неверное решение одной чертой.
-
Использование корректора недопустимо.
-
При написании математических терминов (в случае затруднения) используйте терминологический словарь.
Алгоритм решения геометрических задач
-
Прочитай внимательно условие задачи.
-
Выбери главную ключевую геометрическую фигуру, повторите ее определение и свойства. Из них выделите те свойства, которые будут использованы при решении задачи.
-
Условно разделите лист тетради на две части. Справа запишите краткое условие задачи, начиная с ключевой фигуры (допускаются условные обозначения и символы).
-
Устно проанализируйте условие задачи.
-
Слева выполните чертеж по условию задачи.
-
Задачи на вычисление геометрических величин начинаем со слова «Решение»; задачи на доказательство начинаем со слова «Доказательство»; задачи на построение начинаем со слова «Построение».
-
При решении любой геометрической задачи выделяем этапы решения, каждый этап решения сопровождаем теоретическим обоснованием геометрических фактов.
-
При решении задач на вычисление, сначала записываются равенства в геометрической форме, а затем в алгебраической форме.
-
Проверьте результат вычислений на соответствие геометрическим фактам.
-
Запишите ответ.
Алгоритм решения систем уравнения
Решение систем уравнений 1 степени с двумя переменными способом сложения
-
Умножим обе части каждого уравнения на такое число, чтобы коэффициенты при одной из неизвестных стали противоположными числами в двух уравнениях.
-
Сложим уравнения почленно, получим уравнение с одной переменной.
-
Решим полученное уравнение.
-
Подставим корень уравнения в любое уравнение системы и найдем значение второй переменной.
-
Ответ записываем в виде
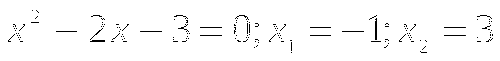 .
.
Пример
![]()
-
Умножим обе части второго уравнения на 3 и сложим уравнения почленно:
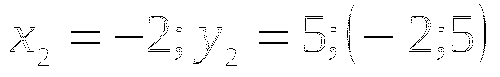
-
Подставим
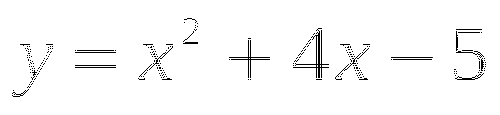 во второе уравнение, найдем y:
во второе уравнение, найдем y: 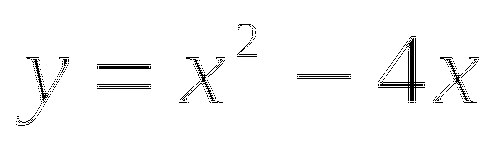
Ответ. ![]() .
.
Решение систем уравнений с двумя переменными способом подстановки
-
Из уравнения первой степени выразим одну переменную через другую.
-
Подставим полученное выражение вместо переменной в другое уравнение.
-
Решаем полученное уравнение.
-
Каждый корень подставим в выражение из п.1 и найдем вторую переменную.
-
Ответ записываем в виде
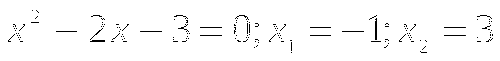 .
.
Пример
![]()
-
Выразим из первого уравнения у через х:
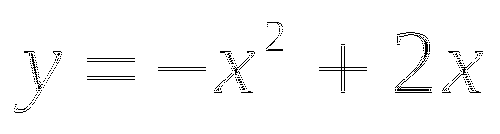 .
. -
Подставим выражение
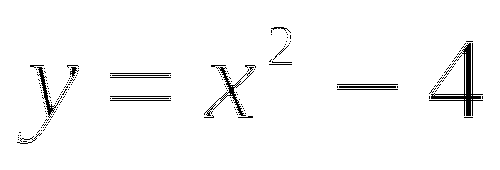 вместо у во второе уравнение:
вместо у во второе уравнение:
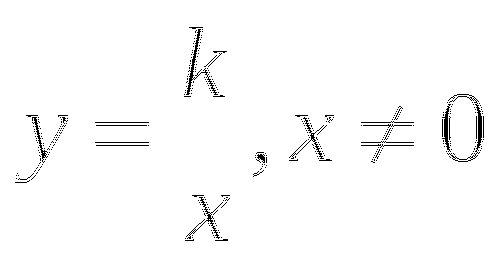
-
Найдем у: если
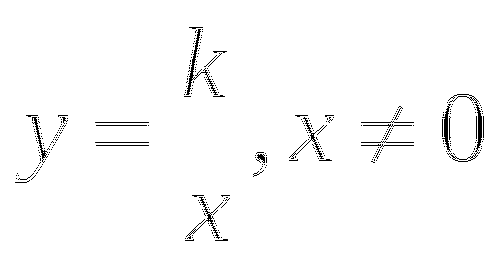 , то
, то  ; если
; если  , то
, то 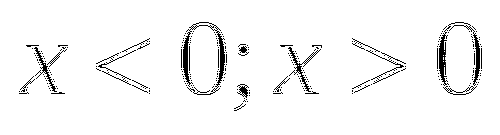 .
.
Ответ. ![]() .
.
Решите самостоятельно а) ![]() б)
б) ![]() в)
в) ![]() г)
г) ![]()
Алгоритм решения систем неравенств
-
Решаем каждое неравенство отдельно.
-
Изображаем решение каждого неравенства системы на одной числовой прямой (штриховкой). Промежуток на оси, где штриховки «пересекутся» и будет решением системы; если общих точек нет, то система не имеет решения.
-
Ответ записываем в виде неравенства или в виде числового промежутка.
Пример
![]()
а) 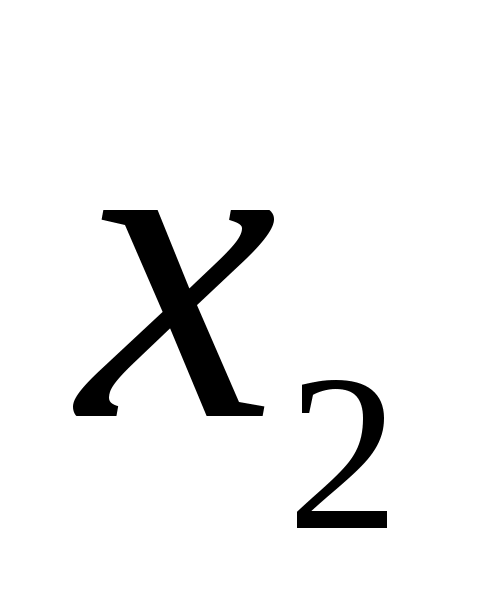 б)
б) 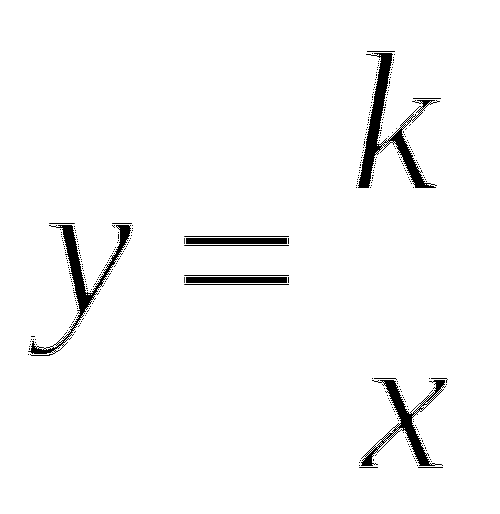 в)
в) ![]()
Ответ. (-5; 1) или ![]() .
.
Пример
![]()
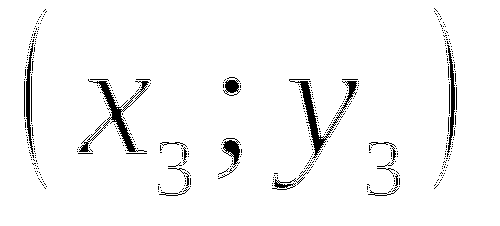
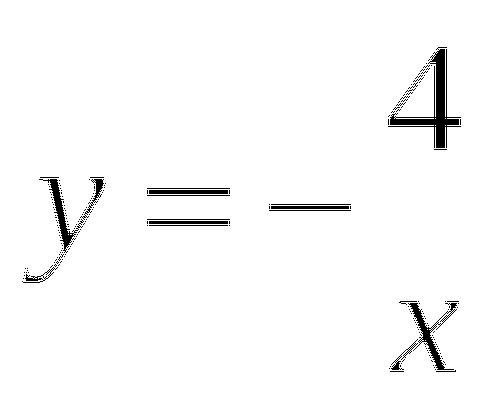
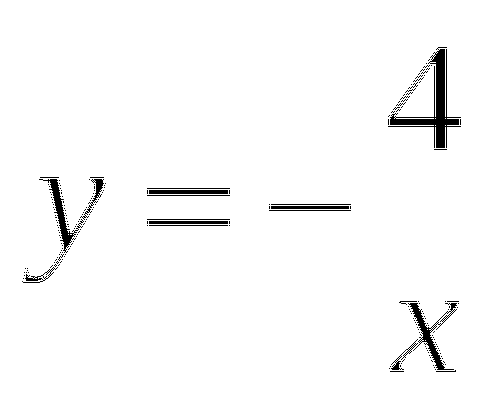
Ответ. ![]() или
или ![]() .
.
Решить самостоятельно
а) ![]() б)
б) ![]() в)
в) ![]() г)
г) ![]() д)
д) ![]()
Алгоритм решения квадратных неравенств ![]() .
.
Графический метод решения квадратных неравенств
-
Рассмотрим функцию
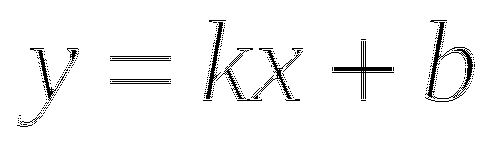 и построим эскиз ее графика, для этого определим направление ветвей параболы и найдем нули функции (если они есть).
и построим эскиз ее графика, для этого определим направление ветвей параболы и найдем нули функции (если они есть). -
По графику определяем, при каких значениях
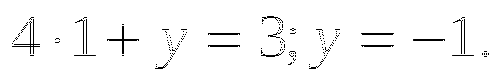 функция принимает положительные и отрицательные значения.
функция принимает положительные и отрицательные значения. -
Решением неравенства являются такие значения
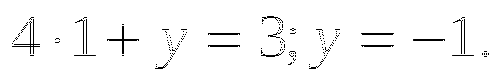 , при которых знак неравенства совпадает со знаком функции.
, при которых знак неравенства совпадает со знаком функции.
Пример
Решить неравенство ![]() .
.
-
Рассмотрим функцию
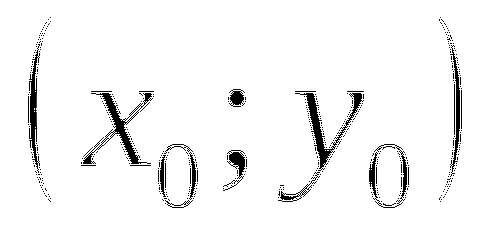 и построим эскиз ее графика: а) ветви параболы направлены вверх, так как
и построим эскиз ее графика: а) ветви параболы направлены вверх, так как 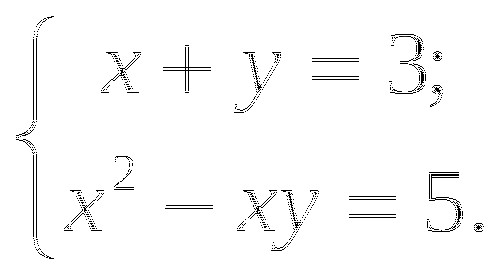 ; б) найдем нули функции
; б) найдем нули функции 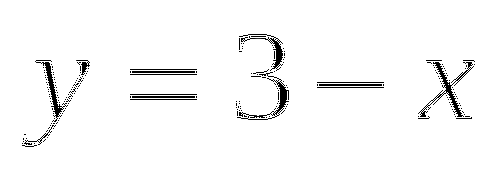 .
. -
По графику определяем, что при
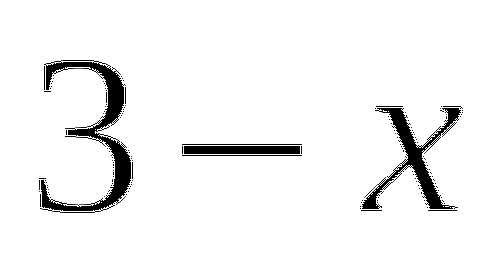 функция принимает положительные значения и при
функция принимает положительные значения и при 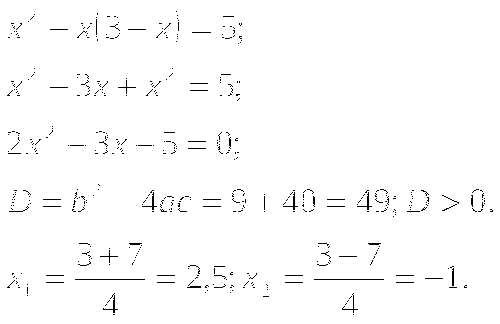 функция принимает отрицательные значения.
функция принимает отрицательные значения. -
Решением неравенства являются такие значения
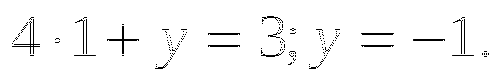 , при которых знак неравенства совпадает со знаком функции, то есть
, при которых знак неравенства совпадает со знаком функции, то есть 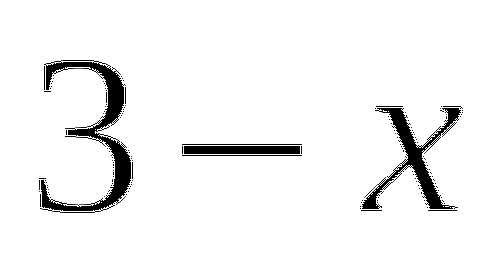 .
.
Ответ. ![]() .
.
Решение квадратных неравенств методом интервалов (применяем при решении квадратных неравенств, для которых ![]() имеет действительные корни)
имеет действительные корни)
-
Найдем такие значения
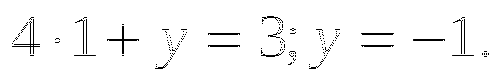 , при которых выражение
, при которых выражение 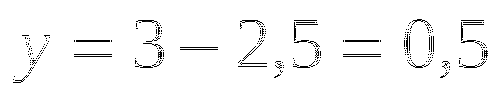 равно нулю.
равно нулю. -
Разложим левую часть неравенства на множители (используем способы разложения многочленов на множители)
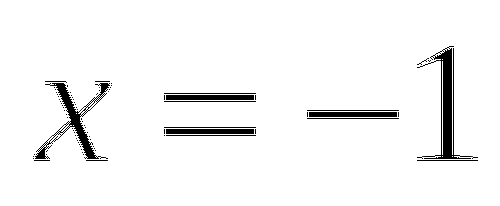 и решаем неравенство
и решаем неравенство 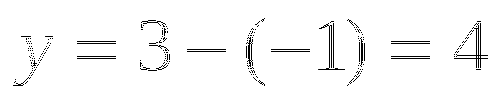 методом интервалов.
методом интервалов. -
Отметим полученные числа на числовой прямой и определим знак выражения
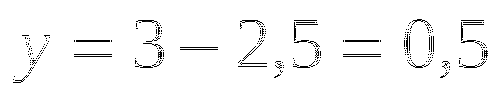 на каждом числовом промежутке (методом пробной точки или с помощью теоремы о старшем коэффициенте квадратного трехчлена).
на каждом числовом промежутке (методом пробной точки или с помощью теоремы о старшем коэффициенте квадратного трехчлена). -
Выбираем решение по знаку неравенства: а)
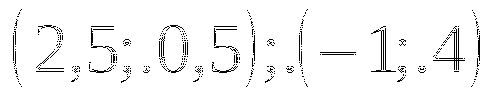 там где «+»; б)
там где «+»; б) 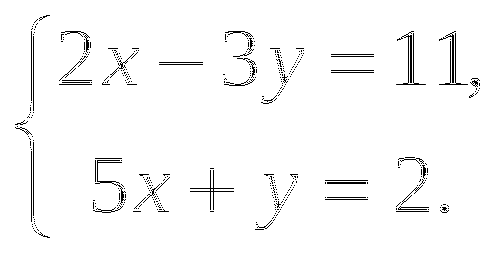 там где «-».
там где «-».
Пример
Решить неравенство ![]() .
.
-
Найдем такие значения
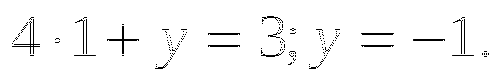 , при которых выражение
, при которых выражение 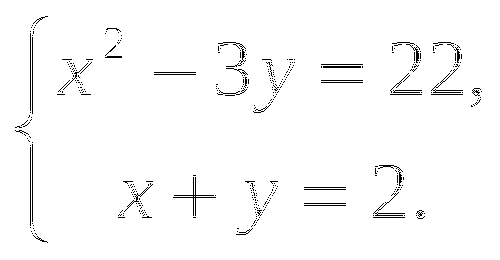 равно нулю:
равно нулю: 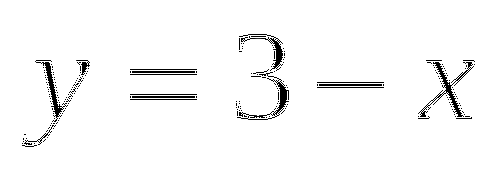 .
. -
Разложим левую часть неравенства на множители:
![]() и решаем неравенство
и решаем неравенство ![]() методом
методом
интервалов.
-
Отметим полученные числа -1 и 3 на числовой прямой и определим знак выражения
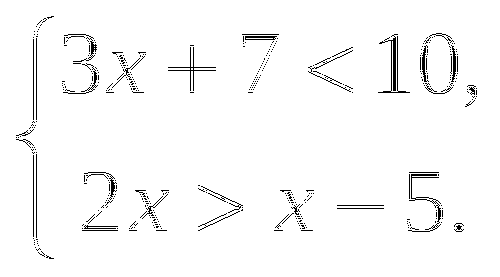 на каждом числовом промежутке.
на каждом числовом промежутке. -
Выбираем решение по знаку неравенства: а)
 .
.
Ответ. ![]() .
.