Проект Мир натуральных чисел учеников 5 класса

Конкурс учебных, учебных и социальных проектов

«ПРОЕКТИРУЕМ БУДУЩЕЕ»

среди учащихся 5-11 классов общеобразовательных учреждений Ульяновской области

Направление работы: Знаки и знаковые системы

Тема проекта:

«Путешествие в мир натуральных чисел»

Выполнили: Гишян Лилит

Коваленко Лера

Степанюк Данила

Шманатова Марина

Хабибуллина Алина

учащиеся 5 А класса

МБОУ «Гимназия №13»

г. Ульновск

Руководитель:

Уланова Юлия Анатольевна

учитель математики высшей категории

Ульяновск 2014

Содержание:

1Введение……………………………………………………………………3

2 Числа…………………………………………………………………….....8

2.1 Как люди научились считать? .................................................................9

3 Приборы для вычисления………………………………………………...11

3.1 Абак………………………………………………………………………13

4 Мера………………………………………………………………………..19

4.1 Древнерусские меры длины…………………………………………….20

4.2 Исследования …………………………………………………………....24

5 Арифметика………………………………………………………………...25

5.1 Л.Ф. Магницкий…………………………………………………………26

5.2 С.А. Рачинский…………………………………………………………..30

5.3 Л.Н. Толстой……………………………………………………………...32

5.4. Решение задач из учебника «Арифметика» А. Пчёлко 1967 год……..35

6 Литература…………………………………………………………………..41

Авторы проекта

Степанюк Данила, Коваленко Лера, Гишян Лилит, Хабибуллина Алина

Предмет и класс

Математика 5 класс

Тема

"Натуральные числа»

Аннотация проекта

Учебный проект рассчитан на учащихся 5 классов, и предназначен для организации и проведения занятий по теме «Натуральные числа», а также для развития интереса к математике, расширения кругозора учащихся, повторения понятий цифра и число.

Цель проекта

Нас очень заинтересовала данная тема. Мы хотели узнать много нового о числах. Ведь мир чисел очень загадочен и интересен. Эта тема является актуальной, потому что числа очень важны в нашем мире. Если бы не было в мире чисел, то мы не знали бы, сколько нам лет, в каком веке или году мы живём. Мы спросили у учителя: « Как люди научились считать, записывать числа?» Она посоветовала самим разыскать необходимый материал. Поэтому и возник этот проект.

Направляющие вопросы

Все ли мы знаем о натуральных числах?

Натуральные числа: что мы о них еще не знаем?

Основополагающий вопрос:

Что есть число?

Проблемные вопросы:

1. Как люди научились считать?

2. Где мы используем числа в повседневной жизни?

Учебные вопросы:

1.1. Как люди считали в древности?

1.2. Когда появилось первое число?

1.3. Какие способы счета вы знаете?

1.4. Как можно записать число?

1.5. Сколько чисел используют для записи цифр?

2.1. Какие инструменты для вычисления мы знаем?

2.2. Где мы их использует в повседневной жизни?

2.3. Какие приборы для вычисления мы используем в повседневной жизни?

3.1. Какие меры измерения длины мы знаем?

3.2. Какие инструменты измерения длины мы знаем?

Ход работы над проектом

1. Подготовительный этап.

Занятие 1.

• Презентация проекта

• Определение темы и цели

• Обсуждение информации

2. Основной этап

Занятие 2.

• Выявление тем для исследования

• Формирование проблемных вопросов

• Отбор желающих заниматься проектом

• Распределение задач между учениками

Занятие 3

• Определение источника информации

• Определение способа сбора информации

• Определение представления результатов исследования

• Ознакомление учащихся с критериями оценивания итоговых работ

Занятие 4

• Предварительный просмотр информации

• Исследования учащихся

3. Заключительный этап.

Занятие 5

• Представление и защита проекта

• оценивание проделанной работы

• Награждение

Лист планирования по теме:

«Числа»

Основополагающий вопрос: что есть число?

Проблемный вопрос: как люди научились считать?

Гипотеза: возможен ли счёт без чисел?

Цель : показать этапы возникновения чисел.

Что я знаю: что такое натуральные числа и какие арифметические действия можно выполнять с ними.

Что найти:

• Как люди считали в древности?

• Когда появилось первое число?

• Какие способы счёта были?

• Как записывались числа?

Ответственный: Степанюк Д.

Лист планирования по теме:

«Приборы для вычисления»

Основополагающий вопрос: что есть число?

Проблемный вопрос: где используют числа в повседневной жизни?

Гипотеза: были ли другие приборы для выполнения арифметических действий?

Что я знаю: для вычисления используют компьютер и калькулятор

Что найти:

• Какие ещё приборы используют для выполнения арифметических действий?

• Как давно они появились?

• Люди каких профессий их использовали?

Ответственный: Хабибуллина А.

Лист планирования по теме:

«Мера»

Основополагающий вопрос: что есть число?

Проблемный вопрос: почему величина измерения -мера?

Гипотеза: были ли другие приборы для вычисления длины?

Что я знаю: для измерения используют линейку

Что найти:

• Какие меры длины мы знаем?

• Какие инструменты для измерения длины мы знаем?

• Как измеряли длину в древней Руси?

Ответственный : Гишян Л.

Лист планирования по теме:

«Арифметика»

Основополагающий вопрос: что есть число?

Проблемный вопрос: что такое арифметика?

Гипотеза: когда и кем издавался учебник «Арифметика» в России?

Что я знаю: арифметика- раздел математики.

Что найти:

• Кто издал учебник «Арифметика» в России?

• С.А. Рачинский и Л.Н. Толстой- авторы учебника арифметики в России?

• Представление учебника «Арифметика» А Пчёлко 1967 года и решение задач из него

Ответственный: Коваленко Л.

«Числа»

Как люди научились считать?

Счет появился тогда, когда человеку потребовалось информировать своих сородичей о количестве обнаруженных им предметов. Сначала люди просто различали один предмет перед ними или нет. Если предмет был не один, то говорили «много». Первыми понятиями математики были "меньше", "больше" и "столько же".

Пальцы сыграли немалую роль в истории счета, особенно когда люди начали обмениваться друг с другом предметами своего труда. Так, например, желая обменять сделанное им копье с каменным наконечником на пять шкурок для одежды, человек клал на землю свою руку и показывал, что против каждого пальца его руки нужно положить шкурку. Одна пятерня означала 5, две- 10. Когда рук не хватало, в ход шли и ноги. Две руки и одна нога - 15, две руки и две ноги - 20. Следы счета на пальцах сохранились во многих странах. Так, в Китае и Японии предметы домашнего обихода (чашки, тарелки и др.) считают не дюжинами(по12 штук) и полудюжинами, а пятерками и десятками. Во Франции и в Англии и поныне в ходу счет двадцатками.

Специальные названия чисел имелись поначалу только для одного и двух. Числа же больше двух называли с помощью сложения: 3 - это два и один, 4 - это два да два, 5 - это два, еще два и один.

Названия чисел у многих народов указывают на их происхождение. Так, у индейцев -два - глаза,у тибетцев -два - крылья, у других народов один - луна, пять - рука.

Название цифр у австралийских племен

1 - энэа, 2 - петчевал, 3 - петчевал-энэа 4 - петчевал-петчевал

1 - мал, 2 - булан, 3 - гулиба, 4 - булан-булан, 5 - булан-гулиба,

6 - гулиба-гулиба

А на берегах реки Амазонки было обнаружено племя, которое знало только три числа- 1, 2 и 3, причем число 3 называлось"поэттаррароринкоароак".

Вот как трудно было людям научиться считать!

Для записи чисел древние египтяне употребляли иероглифы, означающие (последовательно): единицу, десять, сто, тысячу, десять тысяч, сто тысяч (лягушка), Полагают, что иероглиф для сотни изображает измерительную веревку, для тысячи - цветок лотоса, для десяти тысяч - поднятый кверху палец, а для десяти миллионов - всю Вселенную. Все остальные числа составлялись из основных с помощью только одной операции - сложения. При этом запись производилась не слева направо, как у нас, а справа налево.

Самые древние из дошедших до нас математических записей высечены на камне, но наиболее важные свидетельства древнеегипетской математической деятельности запечатлены на гораздо более хрупком и недолговечном материале - папирусе. Два таких документа - папирус Ринда, или египетского писца Ахмеса (ок. 1650 до н.э.)

А вот система нумерации и вычислений, которая сложилась в Индии примерно к VI веку нашей эры, оказалась такой удобной и удачной, что ею сейчас пользуются во всем мире. Европейцы познакомились с ней в X - XIII веках через арабов, которые первыми оценили достоинства этого способа записи чисел, усвоили и перенесли в Европу, поэтому новые цифры в Европе стали называть арабскими.

Форма индийских цифр претерпевала многообразные изменения. Та форма, в которой мы их пишем, установилась в 16 веке.

Арабы были первыми «чужими», которые заимствовали цифры у индийцев и привезли их в Европу. Чуть позже арабы упростили эти значки, они стали выглядеть вот так: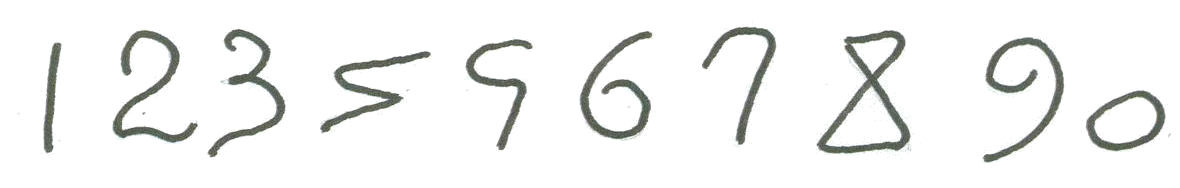

Вот, оказывается, какая длинная история у этих знакомых значков!

Значительно позднее цифры стали изображать иначе.

Из арабского языка заимствовано и слово «цифра» (по-арабски «сыфр»), означающее буквально «пустое место» (перевод санскритского слова «сунья», имеющего тот же смысл).

«Приборы для вычисления»

Аба́к (др.-греч. ἄβαξ, ἀβάκιον, лат. abacus - доска) - счётная доска, применявшаяся дляарифметических вычислений приблизительно с V века до н. э. в Древней Греции, Древнем Риме.

Доска абака была разделена линиями на полосы, счёт осуществлялся с помощью размещённых на полосах камней или других подобных предметов. Камешек для греческого абака назывался псифос; от этого слова было произведено название для счёта - псифофория, «раскладывание камешков» (заглавие книги об индийской арифметике Максима Плануда, умершего в 1310 году, «Псифофория индийцев»)^[1].

Древний Вавилон

Впервые абак появился, вероятно, в Древнем Вавилоне. 3 тыс. лет до н. э. Первоначально представлял собой доску, разграфлённую на полосы или со сделанными углублениями. Счётные метки (камешки, косточки) передвигались по линиям или углублениям. В 5 в. до н. э. в Египте вместо линий и углублений стали использовать палочки и проволоку с нанизанными камешками.

Древняя Индия

Абаком пользовались и народы Индии. Арабы знакомились с абаком у подчинённых ими народов. В заглавиях многих арабских руководств по арифметике фигурируют слова от корня «пыль».

Западная Европа, VIII-X века

У восточных арабов, как и у индийцев, абак был скоро вытеснен индийской нумерацией, но он крепко держался у западных арабов, захвативших в конце VIII века и Испанию. В X веке здесь познакомился со счётом на абаке француз Герберт (940-1003), написавший об этом книгу (980-982) и пропагандировавший сам и через своих учеников употребление абака^[2]. Вместо камешков при счёте на абаке употреблялись и жетоны с начертанными на них числовыми знаками, или римскими цифрами, или особыми числовыми знаками - апексами. Апексы Герберта по форме близки к цифрам гобар западных арабов. Апексы Герберта и его 27-колонный абак, предмет удивления его современников (воспроизведены в реставрированном виде по различным рукописям профессором Н. М. Бубновым, профессором истории Киевского университета, начало XX века). Усилиями многочисленных учеников и последователей Герберта и благодаря его влиянию как папы римского (Сильвестра II, 999-1003) абак получил широкое распространение в Европе. Следы этого распространения удержались, между прочим, в различных языках. Английский глагол to checker, или chequer, означает графить - словом от этого же корня называется клетчатая материя^[1], the cheque, или check - банковый чек, exchequer - казначейство. Последний термин происходит от того, что в банке расчёты велись на абаке, основа которого заключалась в разграфлённой доске. Английское государственное казначейство до последнего времени называлось Палатой шахматной доски - по клетчатому сукну, которым был покрыт стол заседаний. Клетчатая скатерть служила абаком при вычислениях. Возникшая в XII веке Палата шахматной доски была верховным финансовым управлением и высшим судом по финансовым вопросам до 1873 года

В Европе абак применялся до XVIII века. В Средние века сторонники производства арифметических вычислений исключительно при помощи абака - абацисты - в течение нескольких столетий вели ожесточённую борьбу с алгоритмиками - приверженцами возникших тогда методов алгоритмизации арифметических действий.

Мезоамерика, X век

Ацтекские счёты возникли приблизительно в X веке и изготавливались из зёрен кукурузы, нанизанных на струны, установленные в деревянной раме.

Центральные Анды, XVI век

В Империи инков применялось счётное устройство юпана (в паре с кипу), имевшая разновидности: арифметическая юпана, геоюпана и др. В юпане, по-видимому, использовалась фибоначчиева система счисления.

Дальний Восток

В странах Востока распространены китайский аналог абака - суаньпань и японский - соробан. Конструкции принципиально аналогичны, используют десятичную систему счисления, хотя японский вариант несколько экономичнее (в китайском, как и в русских счётах, используются «лишние» с точки зрения математики косточки). Для китайского и японского абака существует скрупулёзно разработанный набор алгоритмов, позволяющих механически (то есть не занимаясь дополнительными вычислениями в уме или на бумаге) выполнять все четыре арифметических действия и даже извлекать квадратные и кубические корни.

Японский соробан по сей день активно применяется, несмотря на повсеместное распространение электронных калькуляторов. В Японии использование соробана является элементом школьной программы обучения счёту в младших классах. Также в Японии и странах, имеющих значительную японскую диаспору, счёт на соробане популярен как вид развлечения или своеобразный спорт.

Россия

Десятичный абак, или русские счеты, в которых используется десятичная система счисления и возможность оперировать четвертями, десятыми и сотыми дробными долями появились в России на рубеже XV - XVI веков и активно применялись в торговле вплоть до последнего десятилетия XX века. От классического абака счеты отличаются увеличением разрядности каждого числового ряда и конструкцией. Ещё одна характерная особенность русских счёт - специально выделенный разряд для счёта в четвертях. С момента своего возникновения счеты практически не изменились.

С появлением дешёвых электронных калькуляторов счёты практически полностью вышли из употребления. Ещё раньше, в начале 1980-х годов, обучение пользованию счётами было исключено в СССР из школьной программы.

«Мера»

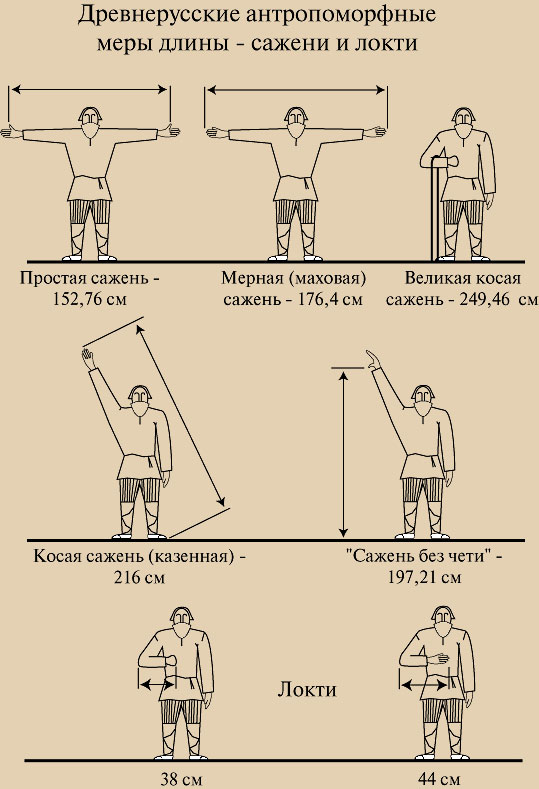
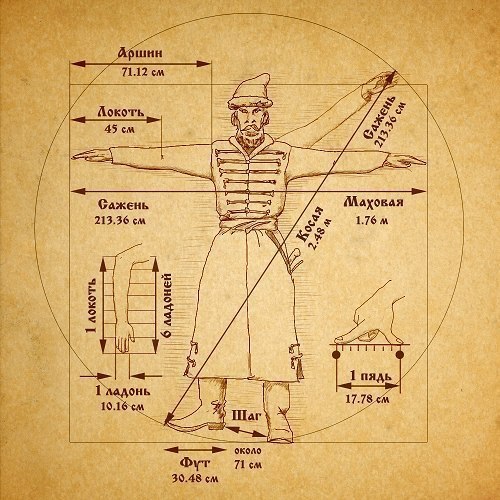
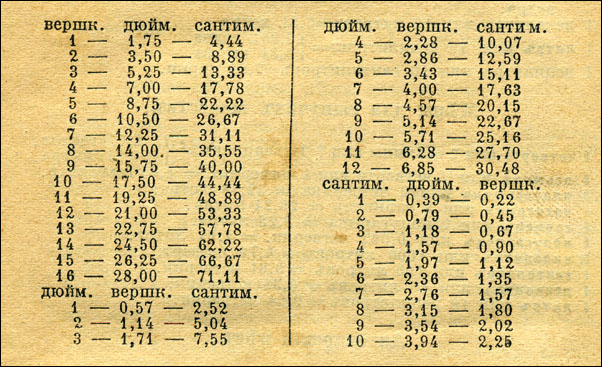
«Арифметика»

Л.Ф.Магницкий

Магницкий - выдающийся педагог-математик первой половины XVIII века, автор «Арифметики», одной из самых замечательных книг XVIII века, Магницкий первый познакомил наших предков с математикой в редком для своего времени объёме и показал её большое практическое значение. В этом главная заслуга Магницкого перед историей математического образования в России. Не менее важна его заслуга как первого учителя русских моряков, преодолевшего с успехом громадные затруднения, которые встретились ему при изложении на русском языке основ мореходной науки.

Сведения о жизни и деятельности Магницкого очень скудны. Магницкий родился 9 (10) июня 1669 года в Москве. Родители Магницкого были русские люди, но к какому сословию они принадлежали и чем занимались - до последних дней оставалось неизвестным. Ничего не известно также о том, учился ли Магницкий, где или у кого, или он был в полном смысле этого слова самородком и самоучкой.

Тридцати двух лет Магницкий стал учителем математики первой русской школы, в которой изучению этой науки было отведено видное место, а именно, математико-навигацкой школы, учрежденной в 1701 году. В этой школе русских юношей обучали арифметике, геометрии, тригонометрии с приложением к геодезии и астрономии, навигации плоской и меркаторской, математической географии, ведению вахтенного журнала Учителями математико-навигацкой школы были назначенные еще в 1698 году англичане: для «науки математической» - Андрей Фархварсон, для «науки навигацкой» - Стефан Гвин и Ричард Грейс. Помощники Фархватсона в 1702 году был назначен Магницкий, известный руководству математико-навигацкой школы как лучший математик Москвы того времени. Тогда же были отпущены средства на составление и печатание учебника Магницкого по математике.

Преподавание в этой школе шло в следующем порядке: ученики, обучающиеся арифметике, после экзамена у Магницкого переводились в следующий класс, класс геометрии; обучавшиеся геометрии переводились в класс тригонометрии и т.д. Магницкий, обучавший арифметике, геометрии и тригонометрии, вначале преподавал также и навигацию. Но после ссоры с англичанами излагал ученикам только одну тригонометрию, и ученики переводились от него к иноземным учителям. По окончании курса Фархватсон и Магницкий подавали списки «окончивших обучение и готовых к практике» сначала в оружейную палату, а потом в приказ военно-морского флота.

В 1715 году последовал указ Петра I об учреждении в Петербурге морской академии. С этого года математико-навигацкая школа несколько изменила свой характер: обучение военным наукам было перенесено во вновь открывшуюся морскую академию, а в московской школе стали учить только арифметике, геометрии и тригонометрии.

С момента открытия морской академии Магницкий стал старшим учителем математико-навигацкой школы и заведующим его учебной частью. С 1832 года Магницкий заведовал распорядительной и хозяйственной частью математико-навигацкой школы

Магницкий руководил математико-навигацкой школой до последних дней своей жизни. Он умер 19 (30) октября 1739 года и погребен в Москве.

«Арифметика» Л.Ф. Магницкого

Магницкий представил свою «Арифметику» 21 ноября 1701 года для публикации. «Арифметика» Магницкого была написана на славянском языке.

Учебник состоит из двух книг: « Арифметики политики, или гражданской» и «Арифметики логистики, не ко гражданству токмо, но и к движению небесных кругов принадлежащей».

Первая книга разделена на пять частей, вторая на три части. В первой части первой книги излагаются правила нумерации, четыре действия над целыми числами и способы их проверки. Далее идут именованные числа, которым предпосылается обширный трактат о древних еврейских, греческих и римских деньгах, мерах и весах Голландии и Пруссии, мерах и деньгах Московского государства, три сравнительные таблицы мер, веса и денег. Этот трактат, отличающийся замечательными подробностями, ясностью и точностью, свидетельствует о глубокой эрудиции и начитанности Магницкого.

Даже и теперь указанный раздел «Арифметики» Магницкого может принести известную пользу при историческом исследовании, так как дает сведения о том, как наши предки измеряли землю, сыпучие вещества, какие у них были деньги и т.д.

Во второй части подробно излагаются дроби, в третьей и четвертой - «задачи на правила», очень остроумно составленные и имевшие для того времени практическое значение, в пятой части излагаются основные правила алгебраических действий, прогрессии и корни. Эта часть содержит множество примеров приложения алгебраического материала к военному и морскому делу.

Главное достоинство «Арифметики» Магницкого - в полноте содержания. Это не просто арифметика, а целый курс математики с приложением ее к мореплаванию. Правда, арифметику Магницкий считал краеугольным камнем математического образования и обработал ее в своей книге исключительно тщательно. Он использовал новинки в области арифметики, ввел новые наименования; «миллион», «биллион» и т.д., сделав тем самым крупный шаг вперед, возвел нуль в ранг числа, причислив его к «перстам» (первым десяти числам) и тем самым на много опередил свое время; поместил множество объяснительных примеров («прикладов»), включая примеры «неких увеселительных действий, через арифметику употребляемых», обнаружил большой педагогический талант при изложении действий над целыми числами и обыкновенными дробями.

Несмотря на эти недостатки, алгебраические и арифметические сведения в «Арифметике» Магницкого сыграли свою роль как впервые приведенные в некоторую систему общедоступные математические сведения, выходящие за пределы собственно арифметики.

Учебник математики Магницкого был труден для понимания не только учеников, но и учителей того времени. Более доступной его частью была арифметика; но даже и эта часть нуждалась в значительной переработке, чтобы быть широко использованной в цифирных школах и в домашнем ученье.

В предисловии к «Арифметике» Магницкий писал: «будет сей труд добре пользовать русский весь люд». Это желание вполне сбылось. Его книга помогла ученикам математико-навигацкой школы дать в 1726-1734 годах материал для первой «генеральной карты всея Руси» и первого географического атласа. Его же книга стимулировала М. В. Ломоносова к естественно-научному образованию.

Сергей Александрович Рачинский

(1833-1902)

Сергей Александрович Рачинский - российский учёный, педагог, просветитель, профессор Московского университета, ботаник и математик.

C 1875 года, несмотря на то что Рачинские - дворянский род, всецело посвятил себя народной школе в селе Татеве Бельского уезда Смоленской губернии. Переселясь из барского дома в школу, он начал жить одною жизнью со своими учениками.

Рачинский весьма интересен как педагог практик, поднявший в своей сельской школе преподавание арифметики на очень высокую ступень, особенно это относится к устному счету и решению задач.

Сергей Рачинский оставил в наследие свой знаменитый задачник «1001 задача для умственного счета», а также книги «Арифметические забавы» и «Геометрические забавы».

«Устный счёт. В народной школе С. А. Рачинского». Это картина русского художника Николая Петровича Богданова-Бельского была написана в 1895 году, а сейчас висит в Третьяковской галерее.

</

Лев Николаевич Толстой

Родился 28 августа 1828 года в имении матери Ясной Поляне Крапивенского уезда Тульской губернии. Семья Толстого принадлежала к богатому и знатному графскому роду. К моменту рождения Льва в семье уже было три сына- Николай(1823-1860), Сергей( 1826-1904) и Дмитрий (1827-1856), а в 1830 году родилась младшая сестра Мария.

Спустя несколько лет умерла мать. После смерти матери, осиротевших детей, взяла на воспитание дальняя родственница Т. А. Ергольская. В 1837 году семья переехала в Москву, т.к. старшему брату Николаю необходимо было готовиться к поступлению в университет. Но в семье внезапно произошла трагедия- скончался отец., оставив дела в плохом состоянии. Трое младших детей были вынуждены вернуться в ясную поляну под воспитание Т.А. Ергольской и тётки отца, графини А.М. Остен-Сакен. Здесь Лев Толстой оставался до 1840 года. В этом году умерла графиня А.М. Остен-Сакен и детей переселили в Казань к сестре отца П.И. Юшковой.

Толстой на первом этапе получал образование под руководством грубоватого гувернёра- француза Сен-Тома. В дальнейшем его заменил добродушный немец Р ессельман.

В 1843 Толстой поступил в Казанский университет на отделение восточных языков философского факультета, затем перевелся на юридический факультет, где проучился неполных два года: занятия не вызывали у него живого интереса и он со страстью предался светским развлечениям. Весной 1847, подав прошение об увольнении из университета "по расстроенному здоровью и домашним обстоятельствам", Толстой уехал в Ясную Поляну с твердым намерением изучить весь курс юридических наук (чтобы сдать экзамен экстерном), "практическую медицину", языки, сельское хозяйство, историю, географическую статистику, написать диссертацию и "достигнуть высшей степени совершенства в музыке и живописи".

В 1851 старший брат Николай, офицер действующей армии, уговорил Толстого ехать вместе на Кавказ. Почти три года Толстой прожил в казачьей станице на берегу Терека, выезжая в Кизляр, Тифлис, Владикавказ и участвуя в военных действиях (сначала добровольно, потом был принят на службу). В 1854 Толстой получил назначение в Дунайскую армию, в Бухарест. Скучная штабная жизнь вскоре заставила его перевестись в Крымскую армию, в осажденный Севастополь, где он командовал батареей на 4-м бастионе, проявив редкую личную храбрость (награжден орденом св. Анны и медалями). После штурма 27 августа 1855 года Лев Николаевич Толстой был отправлен в Петербург. Там он знакомится с сотрудниками журнала «Современник» с Н.А. Некрасовым, И.С. Тургеневым, И.А. Гончаровым,Н.Г. Чернышевским.

Осенью 1856 Толстой, выйдя в отставку, уехал в Ясную Поляну, а в начале 1857 - за границу. Он побывал во Франции, Италии, Швейцарии, Германии Затем вернулся в Москву, а потом - в Ясную Поляну.

В сентябре 1862 Толстой женился на восемнадцатилетней дочери врача Софье Андреевне Берс и сразу после венчания увез жену из Москвы в Ясную Поляну, где полностью отдался семейной жизни и хозяйственным заботам. За 17 лет совместной жизни у них родилось 13 детей.

В начале 70-х Толстой снова проявляет интерес к педагогике, пишет «Азбуку», сочиняет басни и рассказы, которые составили четыре «Русские книги для чтения». Лев Николаевич Толстой писал детские рассказы для крестьянских детей, которые обучались в школе Ясной Поляны. Работа Л.Н. Толстого, как педагога, началась в 1859 году. Его школу посещало небольшое количество крестьянских детей. Это были и мальчики, и девочки. Школа обучала детей абсолютно бесплатно. Лев Николаевич Толстой специально для школы написал «Азбуку » и «Арифметику». На них выросло не одно поколение. Л.Н. Толстой считал что в книге ребёнок должен черпать не только знания, но и учиться доброте, правильному поведению с себе подобными и природой.

В начале 1900 г он увлекается простым физическим трудом, становится вегетарианцем, отдаёт семье всё своё состояние, отказывается от прав литературной собственности

10 ноября 1910 гола Толстой тайно покинул Ясную Поляну, но по дороге сильно заболел. 20 ноября 1910 года на станции Астапово Рязано- Уральской железной дороги Лев Николаевич Толстой умер.

\

Решение задач из учебника «Арифметика»

А.Пчёлко 1967 год

ЛИТЕРАТУРА

1. Депман И.Я., Виленкин Н.Я. За страницами учебника матема ики. - М.: Просвещение, 1989.

2. Крейг А. и Росни К. Наука. Энциклопедия. - М.: «Росмэн», 1994.

3. Математика: Учебник-собеседник для 5-6 классов средней школы / Шаврин Л.Н., Гейн А.Г., Коряков И.О., М.В. Волков М.В. - М.: Просвещение, 1989.

4. Ризванова Х.Я. Книга для внеклассного чтения по математике. - Уфа: Китап, 1998.

5. Шпорер З. Ох, эта математика! - М.: педагогика, 1985.

6. Энциклопедический словарь юного математика / Сост. Савин А.П. - М.: Педагогика, 1989.