Разработка урока математики в 7 классе по теме 'Теоремы об углах, образованных двумя параллельными прямыми и секущей'

Технологическая карта открытого урока

Предмет: Геометрия Класс: 7

Базовый учебник: Геометрия. 7-9 классы: учебник для общеобразовательных учреждений/ Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. - М.: Просвещение, 2010.

Дата проведения урока: 20.01.2015

Тема: Теоремы об углах, образованных двумя параллельными прямыми и секущей.

Цель: сформулировать и доказать теоремы об углах, образованных двумя параллельными прямыми и секущей.

Задачи урока:

• повторить признаки параллельности прямых;

• узнать, какая теорема называется обратной данной;

• сформулировать и доказать теоремы, обратные теоремам о признаках параллельности прямых;

• апробировать алгоритм доказательства методом от противного

Тип урока: урок «открытия нового знания»

Оборудование: экран, мультимедийный проектор, стационарный и мобильный компьютер, видеоурок, презентации, тесты по теме урока, карточки для работы в паре, листы самооценки и рефлексии

СТРУКТУРА И ХОД УРОКА

№

Этап урока

Цель этапа

Деятельность учителя

Деятельность обучающихся

Формируемые

УУД

1

2

3

4

5

6

1.

Мотивация к учебной деятельности (организационный момент.)

1) включение учащихся в учебную деятельность;

2) организовать деятельность учащихся по установке тематических рамок

3) создать условия для возникновения у ученика внутренней потребности включения в учебную деятельность

Приветствие, проверка подготовленности к учебному занятию, организация внимания детей, мотивация детей на познавательную деятельность под девизом «Величие человека в его способности мыслить» (Паскаль)

Включаются в деловой ритм урока, психологически настраиваются на познание нового, отвечают на вводные вопросы учителя, дают первоначальную формулировку темы и цели урока

-организация своей учебной деятельности (Р);

-самоопределение, мотивация учения (Л)

2.

Актуализация опорных знаний

1) организовать актуализацию знаний и изученных способов действий, достаточных для построения нового знания: 2) зафиксировать актуализированные знания в речи;

3) зафиксировать актуализированные знания в знаках;

4) мотивировать к выполнению пробного действия;

5) организовать самостоятельное выполнение пробного учебного действия;

Организует устный опрос и работу с таблицей в парах,

направленную на актуализацию знаний, самоконтроль и самооценку знаний понятий «определение», «аксиома», «теорема», теорем о признаках параллельности прямых, умение выделять условие и заключение теоремы;

пробное учебное действие по формулированию свойств параллельных прямых

Устно отвечают на вопросы учителя, приводят примеры определений, аксиом, теорем;

В парах работают с таблицами «Признаки и свойства параллельных прямых». Работают с листами самооценки (оценивают себя по критерию «знание признаков параллельности прямых»)

- подведение под понятие (П);

- выражение своих мыслей с достаточной полнотой и точностью (К);

- учет разных мнений (К);

самоконтроль и самооценка (Р);

- выполнение пробного учебного действия (Р);

- фиксирование индивидуального затруднения в пробном действии, самооценка (Р);

3

Выявление места и причины затруднения

1) организовать восстановление выполненных операций;

2) организовать фиксацию места (шага, операции), где возникло затруднение;

3) организовать соотнесение своих действий с используемыми эталонами (алгоритмом, понятием и т.д.);

4) на этой основе организовать выявление и фиксацию во внешней речи причины затруднения - тех конкретных знаний, умений или способностей, которых недостает для решения исходной задачи и задач такого класса или типа вообще.

Организует выявление причины затруднения

Отвечают на вопросы учителя, пошагово восстанавливают свои действия во внешней речи и устанавливают причину затруднений: незнание, что такое обратная теорема

умение вступать в диалог, участвовать в коллективном обсуждении вопроса (К);

логические УУД (П);

4.

Построение проекта выхода из затруднения

организовать построение проекта выхода из затруднения

Организует постановку цели и учебных задач, выбор способов их достижения

Ставят цель и задачи деятельности, выбирают средства и способы её достижения

-самоопределение (Л);

-целеполагание, планирование, прогнозирование (предвосхищение) результата деятельности (Р)

5.

Реализация построенного проекта

Физкультминутка

1) организовать реализацию построенного проекта в соответствии с планом;

2) организовать фиксацию нового знания в речи;

3) организовать фиксацию нового знания в знаках (с помощью эталона);

4) организовать фиксацию преодоления затруднения;

5) организовать уточнение общего характера нового знания (возможность применения нового способа действий для решения всех заданий данного типа)

Организует работу, направленную на «открытие» нового:

понятие «обратная теорема»; формулировка и доказательство обратных теорем, метод доказательства от противного

Организует зарядку для глаз

«Открывают» новое знание с помощью фрагмента видеоурока;

продолжают работу с таблицей: формулируют обратные теоремы, доказывают их в микрогруппах

Выполняют упражнения для глаз

-учебное сотрудничество с учителем и сверстниками (К);

-аргументация своего мнения и позиции в коммуникации (К);

-разрешение конфликтов (К);

- поиск и выделение необходимой информации (П);

анализ, синтез, сравнение, обобщение (П);

контроль и коррекция полученного результата (Р), -здоровьесбереже-ние (Л)

6.

Первичное закрепление с проговариванием во внешней речи

организовать усвоение нового при доказательстве теорем на доске, решении задач на их применение

Организует индивидуальный опрос на доказательство теорем и фронтальную работу с задачами

Представитель группы доказывает свою теорему на доске.

Обучающиеся применяют знания при решении задач

- аналогия (П),

- использование знаково-символических средств (П);

- выполнение действий по алгоритму (П);

- выражение своих мыслей с достаточной полнотой и точностью (К);

7.

Самостоятельная работа с самопроверкой по образцу

1) организовать самостоятельное выполнение учащимися типовых заданий на знание свойств параллельных прямых;

2) организовать соотнесение работы с эталоном для самопроверки;

3) по результатам выполнения самостоятельной работы организовать рефлексию деятельности по применению новых знаний

Организует работу с электронным и печатными тестами по теме урока, самооценку

1 ученица выполняет тест по теме «Параллельные прямые» на компьютере (CD «Уроки геометрии Кирилла и Мефодия»), остальные работают с печатными вариантами тестов («VIDEOUROKI.

NET»)

- самоконтроль и самооценка (Р);

- коррекция (Р);

8

Включение в систему знаний и повторение

1. тренировать навыки использования нового содержания совместно с ранее изученным:

2. выход за рамки программы (знакомство с софизмами)

Предлагает доказать утверждения методом от противного.

Организует беседу об использовании метода в жизни.

Знакомит с софизмами

В минигруппах доказывают утверждения новым методом.

Высказывают предположения о том, где может пригодиться метод в жизни.

Знакомятся с софизмами, пытаются найти ошибки…

- выполнение действий по алгоритму (П);

- выражение своих мыслей с достаточной полнотой и точностью (К);

анализ, синтез, сравнение, обобщение (П);

9.

Рефлексия. Домашнее задание

Цель:

1) организовать фиксацию нового содержания, изученного на уроке;

2) организовать оценивание обучающимися собственной деятельности на уроке;

3) организовать фиксацию неразрешённых затруднений на уроке как направлений будущей учебной деятельности;

4) организовать обсуждение и запись домашнего задания.

Организует подведение итогов урока, дает комментарий к домашнему заданию

Делают вывод о достижении поставленных целей и задач, оценивают свою работу на уроке, высказывают своё отношение к прошедшему уроку, записывают домашнее задание

- рефлексия (Р);

- самооценка на основе критерия успешности (Л);

- адекватное понимание причин успеха/неуспеха в учебной деятельности (Л);

- выражение своих мыслей с достаточной полнотой и точностью (К);

«Величие человека в его способности мыслить»

Б.Паскаль

1. Оргмомент. Мотивация к учебной деятельности.

Приветствие.

-Назовите, пожалуйста, тему нашего урока. Откуда вы её узнали? (прочитали)

- Большую часть информации мы получаем с помощью глаз, зрения. Но не могут ли наши глаза обманывать нас? Я предлагаю вам рассмотреть несколько рисунков. Слайды:

Сравните на глаз длины отрезков АВ и ВС на первых двух рисунках, и определите на глаз прямые или кривые длины на рисунках 3-6.

А теперь воспользуйтесь линейкой и ответьте на эти вопросы еще раз.

Выводы: зрение человека дает не точную, а иногда ошибочную информацию. Что же делать? Измерять?

Самые тщательные измерения оставляют повод для сомнения, так как в них неизбежны ошибки. Кроме того, под рукой может не оказаться измерительных инструментов, да и для всех фигур данного вида невозможно проделать измерения.

Надо учиться рассуждать.

«Искусство рассуждать» - так бы можно было переформулировать тему сегодняшнего урока. Но овладеть этим искусством непросто.

Есть такая наука, которая учит, как нужно рассуждать, чтобы наше мышление было определенным связным, последовательным, доказательным и непротиворечивым. Кто знает, что это за наука? (Логика). Я не сомневаюсь, что в голове у вас много разных мыслей, но эти мысли надо упорядочить, направить в русло полезной работы.

Математика поможет вам справиться с этой задачей. Недаром говорят, что математика это гимнастика для ума.

В Древней Греции всех ораторов учили геометрии. На дверях школы было написано: «Незнающий геометрии да не войдет сюда». Это объясняется тем, что геометрия учит рассуждать и доказывать. Речь человека убедительна, когда он доказывает свои выводы.

Считается, что первыми стали применять доказательство древние грехи (6 век до н.э.) Фалес первым начал игру в «Докажи», которая и продолжается уже 2,5 тысячелетия и конца которой не видно.

Доказательство любой теоремы - это цепочка логических умозаключений, сводящих доказываемую теорему к ранее доказанным теоремам, аксиомам и определениям.

2. Актуализация опорных знаний.

1) Фронтальная работа:

А знаете ли вы, что такое определение? Аксиома? Теорема?

Определение - это предложение, в котором разъясняется смысл того или иного выражения или названия.

Аксиома - это утверждение, устанавливающее некоторое свойство и принимаемое без доказательств.

Теорема - это утверждение, справедливость которого устанавливается путём рассуждений.

- Какие аксиомы вы знаете? А теоремы?

2) Работа в парах (3 мин.):

Вставьте недостающие слова и числа в таблицу:

№ п/п

Признаки

параллельных прямых

Свойства параллельных прямых (обратные теоремы)

1

Формулировка теоремы

Если при пересечении двух прямых секущей накрест____________________углы_______________, то прямые параллельны

Если

то

Чертёж

а с

1

в 2

а с

1

в 2

Условие (Дано)

прямые а, в; с - их секущая;

ے1, ے 2 - накрест лежащие;

ے1= ے 2

прямые а, в; с - их секущая;

ے1, ے 2 - накрест лежащие;

__________

Заключение (Доказать)

а // в

__________

2

Формулировка теоремы

Если при пересечении двух прямых секущей соответственные углы____________, то прямые __________________________

Если

то

Чертёж

а с 2

3

в 1

а с 2

3

в 1

Условие (Дано)

прямые а, в; с - их секущая;

ے1, ے 2 - соответственные ;

ے1= ے 2

прямые а, в; с - их секущая;

ے1, ے 2 - соответственные ;

Заключение (Доказать)

______________

_______________

Формулировка теоремы

Если при пересечении двух прямых секущей сумма ________________________ углов равна ___________, то прямые___________________

Если

то

Чертёж

а с

3 2

в 1

а с

3 2

в 1

Условие (Дано)

прямые а, в; с - их секущая;

ے1, ے 2 - односторонние ;

ے1+ ے 2=________

прямые а, в; с - их секущая;

ے1, ے 2 - односторонние ;

Заключение (Доказать)

____________

_______________

3. Выявление места и причины затруднений

-Какой столбик таблицы было легко заполнить? Почему?

-Проверим, как вы справились с этим.

Самооценка.

-Какой столбик пока заполнить трудно? Почему?

4. Построение проекта выхода из затруднения.

-Как вы думаете, какова основная цель нашего урока? (сформулировать и доказать теоремы).

-Для достижения этой цели какую задачу мы уже решили?

-Какие задачи предстоит решить? (Слайд)

-Что может облегчить решение поставленных задач?

5. Реализация построенного проекта.

1. Видеоурок «Теорема о накрест лежащих углах».

Уточнение понимания, что такое «обратная теорема» с опорой на презентацию.

2. Работа в группах.

Задача: сформулировать и доказать обратные теоремы (2 и 3). При затруднении можно использовать презентацию.

6. Первичное закрепление с проговариванием во внешней речи.

Проверка самостоятельной работы. Самооценка.

Решение задач на применение новых теорем (слайд).

7. Самостоятельная работа с самопроверкой по эталону (тест)

1 ученица решает тест на компьютере, остальные распечатанные варианты с проверкой по слайду.

Ответы:

1) Верный ответ: "равны".

2) Верный ответ: "равны".

3) Верные ответы: 3;

4) Верный ответ: 1;

5) Верный ответ: 4;

6) Верный ответ: 3;

7) Верный ответ: 1;

8) Верные ответ: 2;

Самооценка.

8. Включение в систему знаний.

- Сегодня вы встретились с методом доказательства от противного.

-Может ли этот метод пригодиться вам в жизни? В каких профессиях?

- Попробуйте доказать методом от противного (используют памятку):

1) Если в школе 400 учеников, то есть ученики, у которых дни рождения совпадают.

2) Два смежных угла не могут быть тупыми.

Занимательная математика:

- Я хочу вас познакомить с одним математическим понятием - софизмом. Софизм - это заведомо ложное умозаключение, имеющее видимость правила. То есть в доказательстве намеренно допускается ошибка, которая приводит к абсурду.

Так, например, можно доказать, что 1=2.

Слайды:

Найдите ошибку в рассуждениях.

9. Итог урока. Рефлексия. Домашнее задание

- Вспомните, какую цель мы ставили сегодня на урок? Достигли ли мы её? Все ли задачи выполнили?

Заполните лист рефлексии. Оцените свою работу на уроке.

Домашнее задание: Обязательно: вопросы 12-15 на стр. 684

На выбор: Р.Т. № 109, 110. Учебник: №203(а), 209. Дополнительный материал о Фалесе из Милета.

Приложение 1

Лист самооценки ____________________________

Критерий

Справился без ошибок - 3 б.

Допустил не более 1 ошибки - 2 б.

Справился с помощью других или допустил 2-3 ошибки - 1 б.

Не справился - 0 б.

Итоговая отметка:

8-9 б. - «5»,

5-7 б. - «4»,

3-4 б. - «3»

Знание признаков параллельности прямых

Формулировка обратных теорем

Применение знаний (тест)

Приложение 2

Лист рефлексии

1. На уроке я работал

активно / пассивно

2.Своей работой на уроке я

доволен / не доволен

3.Урок для меня показался

коротким / длинным

4. За урок я

не устал / устал

5. Мое настроение

стало лучше / стало хуже

6. Материал урока мне был

понятен / не понятен

полезен / бесполезен

интересен / скучен

Приложение 3.

Тест

Теоремы об углах, образованных двумя параллельными прямыми и секущей

1. Если две параллельные прямые пересечены секущей, то накрест лежащие углы_______________

2. Если две параллельные прямые пересечены секущей, то соответственные углы ______________

3. Если две параллельные прямые пересечены секущей, то ...

Выберите один из 3 вариантов ответа:

1) односторонние углы равны

2) односторонние углы не могут быть равными

3) сумма односторонних углов равна 180°

4. Верно ли утверждение: "Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой"?

Выберите один из 2 вариантов ответа:

1) Верно

2) Неверно

5. На рисунке прямая p параллельна стороне АС треугольника АВС. Чему равен угол ВАС, если градусная мера угла 1 равна 130°?

Изображение:

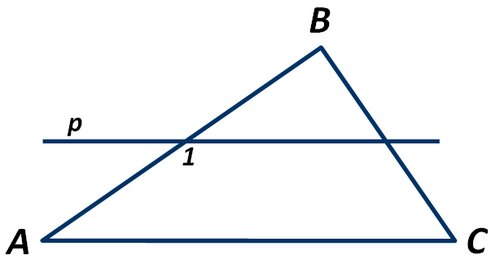
Выберите один из 4 вариантов ответа:

1) 130°

2) 100°

3) 60°

4) 50°

6. На рисунке прямая p параллельная стороне АС треугольника АВС. Чему равна градусная мера угла 1, если угол ВАС равен 30°?

Изображение:

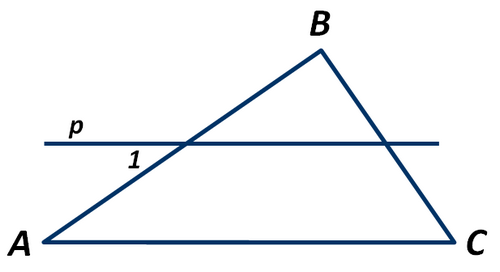
Выберите один из 4 вариантов ответа:

1) 130°

2) 60°

3) 30°

4) 90°

7. На рисунке прямая p параллельна стороне АС треугольника АВС. Чему равен угол 1, если градусная мера угла АСВ равна 65°?

Изображение:

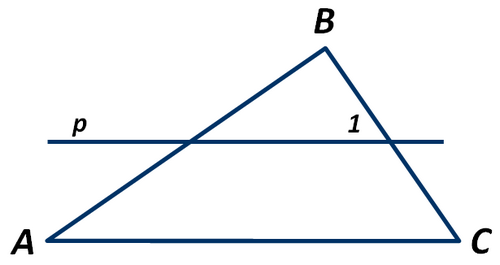
Выберите один из 4 вариантов ответа:

1) 65°

2) 25°

3) 115°

4) 105°

8. Даны две параллельные прямые и секущая. Могут ли быть равными внутренние односторонние углы?

Выберите один из 3 вариантов ответа:

1) Не могут.

2) Могут, если секущая перпендикулярна этим параллельным прямым.

3) Внутренние односторонние углы всегда равны.