- Учителю
- Исследовательский реферат на тему В мире многогранников
Исследовательский реферат на тему В мире многогранников
МБОУ « Средняя общеобразовательная школа № 3»
В мире многогранников
Исследовательский реферат.
Выполнил: ученик 10 «Б» класса
Касумов Рамиз
Научные руководители:
Ханаша Любовь Николаевна,
Лянтор
Содержание
1. Введение...............................................................................................................................
2. История развития многогранников....................................................................................
3.Определение многогранника, его элементы..................................................................
4. Классификация многогранников.......................................................................................
5. Тела Платона.........................................................................................................................
6. Тела Архимеда.....................................................................................................................
7. Звездчатые многогранники................................................................................................
8. Многогранники в искусстве...............................................................................................
9. Многогранники в архитектуре...........................................................................................
10. Музей плодов в Яманаши.................................................................................................
12. Многогранники в природе ..............................................................................................
13. Заключение........................................................................................................................
16. Список используемой литературы……………………………………………………..
17. Приложение 1 …………………………………………………………………………...
18. Приложение 2 …………………………………………………………………………...
19. Приложение 3……………………………………………………………………………
20.Приложение 4…………………………………………………………………….………
Аннотация
Касумов Рамиз
г. Лянтор, МБОУ «СОШ №3», 10 б класс
«В мире многогранников»
руководители: Ханаша Любовь Николаевна, учитель математики
Гороховик Татьяна Георгиевна, учитель математики
Цель работы: изучить мир многогранников, выяснить проявление в природе и применение в искусстве и архитектуре.
Задачи:
-
изучить литературу по выбранной теме;
-
ознакомиться с различными видами многогранников, их свойствами;
-
выяснить, где они встречаются в природе и окружающем нас мире;
-
изготовить модели многогранников для кабинета математики.
Методы исследований: анализ научной литературы, сравнение, моделирование, исторический, фотофиксация.
Основные результаты исследований: изучил историю многогранников, рассмотрел различные виды многогранников, выяснил, где они встречаются в природе и окружающем нас мире, изготовил с одноклассниками модели многогранников для кабинета математики.
Введение
«Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Все вокруг - геометрия». Эти слова, сказанные великим французским архитектором Ле Карбюзье в начале 20 века, очень точно характеризуют и наше время. Мир, в котором мы живем, наполнен геометрией домов и улиц, гор и полей, творениями природы и человека.
Стереометрия довольно сложный раздел геометрии для многих учеников школ, ведь пространственное воображение развито далеко не у всех. К тому же, сам предмет геометрии не вызывает особого энтузиазма у учащихся. «Предмет математики настолько серьезен, что полезно не упускать случая, делать его немного занимательным», говорил Блез Паскаль. Это и послужило причиной выбора темы моей работы: «Мир многогранников». Трудно найти человека, который не имел бы какого-либо представления о многогранниках. С многогранниками мы встречаемся везде - в природе, технике, искусстве, науке, архитектуре. Применение разнообразных геометрических форм придает строениям особый колорит, поднимает человечество на более высокую ступень развития.
Тема работы: «В мире многогранников».
Творческое название: «Глядя на мир нельзя не удивляться!»
Проблема: Существует ли гармония между красотой и многогранностью?
-
Цель работы: систематизация знаний и получение новой информации о многогранниках.
Задачи:
![]() Изучить
литературу о многогранниках.
Изучить
литературу о многогранниках.
![]() Показать
влияние правильных многогранников на возникновение философских
теорий и гипотез.
Показать
влияние правильных многогранников на возникновение философских
теорий и гипотез.
![]() Ознакомиться
с различными видами многогранников, их свойствами.
Ознакомиться
с различными видами многогранников, их свойствами.
![]() Показать
связь геометрии и природы.
Показать
связь геометрии и природы.
![]() Познакомиться с примерами применения многогранников в архитектуре и
искусстве.
Познакомиться с примерами применения многогранников в архитектуре и
искусстве.
![]() Систематизировать найденную информацию.
Систематизировать найденную информацию.
![]() Изготовить модели многогранников для кабинета математики.
Изготовить модели многогранников для кабинета математики.
![]() Создать
презентацию к работе.
Создать
презентацию к работе.
Объект исследования: Математика
Предмет исследования: Многогранники
Гипотеза: Без многообразия геометрических форм окружающий нас мир был бы скучен и однообразен.
История развития многогранников
Первые упоминания о многогранниках известны еще за три тысячи лет до нашей эры в Египте и Вавилоне. Достаточно вспомнить знаменитые египетские пирамиды. Великая пирамида была построена как гробница Хуфу, известного грекам как Хеопс. Он был одним из фараонов, или царей древнего Египта, а его гробница была завершена в 2580 году до н.э. Позднее в Гизе было построено еще две пирамиды, для сына и внука Хуфу, а также меньшие по размерам пирамиды для их цариц. Пирамида Хуфу, самая дальняя на рисунке, является самой большой.

Это правильная пирамида, в основании которой квадрат со стороной 233 м и высота которой достигает 146,5 м. Не случайно говорят, что пирамида Хеопса - немой трактат по геометрии. Пирамида его сына находится в середине и смотрится выше, потому что стоит на более высоком месте.
Наше знакомство с многогранниками начинается уже в начальных классах (куб, прямоугольный параллелепипед) и продолжается до окончания школы. Многогранником называется тело, граница которого является объединением конечного числа многоугольников. [3]
Элементы многогранника
Грань многогранника - это некоторый многоугольник (многоугольником называется ограниченная замкнутая область, граница которой состоит из конечного числа отрезков).
Стороны граней называются ребрами многогранника, а вершины граней - вершинами многогранника. К элементам многогранника, кроме его вершин, ребер и граней, относятся также плоские углы его граней и двугранные углы при его ребрах. Двугранный угол при ребре многогранника определяется его гранями, подходящими к этому ребру. [1]
Классификация многогранников
Выпуклый многогранник - это многогранник, любые две точки которого соединимы в нем отрезком. Выпуклые многогранники обладают многими замечательными свойствами.
Теорема Эйлера: Для любого выпуклого многогранника В-Р+Г=2,
Где В - число его вершин, Р - число его ребер, Г - число его граней.
Теорема Коши: Два замкнутых выпуклых многогранника, одинаково составленные из соответственно равных граней равны.
Выпуклый многогранник считается правильным, если все его грани - равные правильные многоугольники и в каждой его вершине сходиться одно и то же число ребер.
Многогранники имеют красивые формы, например, правильные, полуправильные и звездчатые многогранники. [4]
«Математика владеет не только истиной, но и высшей красотой - красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства.»
Бертран Рассел
Тела Платона
Ни одни геометрические тела не обладают таким совершенством и красотой, как правильные многогранники. "Правильных многогранников так мало, - написал когда-то Л. Кэрролл, - но это весьма скромный по численности отряд сумел пробраться в самые глубины различных наук".
Многогранник, все грани которого представляют собой правильные и равные многоугольники, называют правильными. .
История правильных многогранников уходит в глубокую древность. Начиная с 7 века до нашей эры в Древней Греции создаются философские школы, в которых происходит постепенный переход от практической к философской геометрии.. Большое значение в этих школах приобретают рассуждения, с помощью которых удалось получать новые геометрические свойства.
Одной из первых и самых известных школ была Пифагорейская, названная в честь своего основателя Пифагора. Отличительным знаком пифагорейцев была пентаграмма, на языке математики - это правильный не выпуклый или звездчатый пятиугольник. Пентаграмме присваивалось способность защищать человека от злых духов. Пифагорейцы полагали, что материя состоит из четырех основных элементов: огня, земли, воздуха и воды. Существование пяти правильных многогранников они относили к строению материи и Вселенной. Согласно этому мнению, атомы основных элементов должны иметь форму различных тел:
Вселенная - додекаэдр
Земля - куб
Огонь - тетраэдр
Вода - икосаэдр
Воздух - октаэдр
Почему правильные многогранники получили такие имена? Это связано с числом их граней. Тетраэдр имеет 4 грани, в переводе с греческого "тетра" - четыре, "эдрон" - грань, гексаэдр (куб) имеет 6 граней, "гекса" - шесть, октаэдр - восьмигранник, "окто" - восемь, додекаэдр - двенадцатигранник, "додека" - двенадцать, икосаэдр имеет 20 граней, "икоси" - двадцать.
Позже учение пифагорейцев о правильных многогранниках изложил в
своих трудах другой древнегреческий ученый, философ - идеалист
Платон. С тех пор правильные многогранники стали называться
платоновыми телами. [4] Этим красивым телам посвящена 13-я книга
"Начал" Евклида. Их еще называют телами Платона, т.к. они занимали
важное место в философской концепции Платона об устройстве
мироздания. Четыре многогранника олицетворяли в ней четыре сущности
или "стихии". Тетраэдр символизировал огонь, т.к. его вершина
устремлена вверх. Икосаэдр - воду, т.к. он самый "обтекаемый. Куб
-
землю, как самый "устойчивый. Октаэдр - воздух, как самый
"воздушный". Пятый многогранник, додекаэдр, воплощал в себе "все
сущее", символизировал все мироздание, считался главным.
Гармоничные отношения древние греки считали основой мироздания,
поэтому четыре стихии у них были связаны такой пропорцией:
земля/вода = воздух/огонь. Атомы "стихий" настраивались Платоном в
совершенных консонансах, как четыре струны лиры. Консонансом
называется приятное созвучие. Надо сказать, что своеобразные
музыкальные отношения в Платоновых телах являются чисто
умозрительными и не имеют под собой никакой геометрической основы.
Этими отношениями не связаны ни число вершин Платоновых тел, ни
объемы правильных многогранников, ни число ребер или граней. В
связи с этими телами уместно будет сказать, что первая система
элементов, включавшая четыре элемента - землю, воду, воздух и
огонь, - была канонизирована Аристотелем. Эти элементы оставались
четырьмя краеугольными камнями мироздания в течение многих веков.
Вполне возможно отождествить их, с известными нам, четырьмя
состояниями вещества - твердым, жидким, газообразным и плазменным.
Важное место занимали правильные многогранники в системе гармоничного устройства мира И. Кеплера. Все та же вера в гармонию, красоту и математически закономерное устройство мироздания привела И. Кеплера к мысли о том, что поскольку существует пять правильных многогранников, то им соответствуют только шесть планет. По его мнению, сферы планет связаны между собой вписанными в них Платоновыми телами. Поскольку для каждого правильного многогранника центры вписанной и описанной сфер совпадают, то вся модель будет иметь единый центр, в котором будет находиться Солнце. Проделав огромную вычислительную работу, в 1596 г. И. Кеплер в книге "Тайна мироздания" опубликовал результаты своего открытия. В сферу орбиты Сатурна он вписывает куб, в куб - сферу Юпитера, в сферу Юпитера - тетраэдр, и так далее последовательно вписываются друг в друга сфера Марса - додекаэдр, сфера Земли - икосаэдр, сфера Венеры - октаэдр, сфера Меркурия. Тайна мироздания кажется открытой. Сегодня можно с уверенностью сказать, что расстояния между планетами не связаны ни с какими многогранниками. Впрочем, возможно, что без "Тайны мироздания", "Гармонии мира" И. Кеплера, правильных многогранников не было бы трех знаменитых законов И. Кеплера, которые играют важную роль в описании движения планет.
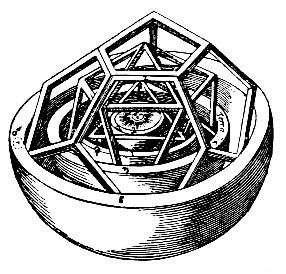
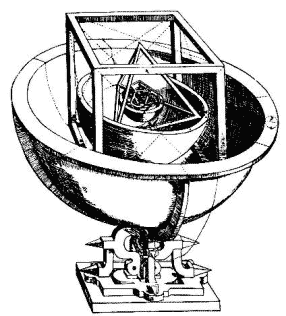
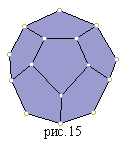
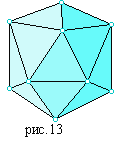
Правильный икосаэдр составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти треугольников.
Все пять правильных многогранников перечислены в таблице, приведенной ниже. В трех последних столбцах указаны N0 - число вершин, N1 - число ребер и N2 - число граней каждого многогранника.0
(число вершин)
N1
(число ребер)
N2
(число граней)
Тетраэдр
4
6
4
Куб
8
12
6
Октаэдр
6
12
8
Икосаэдр
12
30
20
Додекаэдр
20
30
12
Тела Архимеда
Но есть и такие многогранники, у которых все многогранные углы равны, а грани - правильные, но разноименные правильные многоугольники. Многогранники такого типа называются равноугольно-полуправильными многогранниками. Впервые многогранники такое типа открыл Архимед. Им подробно описаны 13 многогранников, которые позже в честь великого ученого были названы телами Архимеда. Это усеченный тетраэдр, усеченный оксаэдр, усеченный икосаэдр, усеченный куб, усеченный додекаэдр, кубооктаэдр, икосододекаэдр, усеченный кубооктаэдр, усеченный икосододекаэдр,



ромбокубооктаэдр, ромбоикосододекаэдр, "плосконосый" (курносый)
куб, "плосконосый" (курносый) додекаэдр. [2]
усеченный тетраэдр усеченный октаэдр усеченный икосаэдр



усеченный гексаэдр усеч додекаэдр ромбоусеченный
кубооктаэдр



ромбоусеченный
икосододекаэдр ромбокубо-октаэдр ромбоикосо-додекаэдр



курносый додекаэдр кубо-октаэдр конусный куб
икосо-додекаэдр 
Конструирование архимедова усеченного икосаэдра из платонова икосаэдра
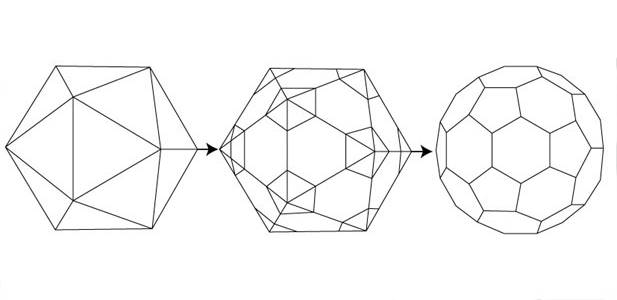
Звездчатые многогранники
Кроме правильных многогранников красивые формы имеют звёздчатые многогранники. Звёздчатый многогранник (звёздчатое тело) - это невыпуклый многогранник, грани которого пересекаются между собой. У звёздчатых многогранников грани попарно соединяются в ребрах, при этом внутренние линии пересечения не считаются рёбрами. Их всего четыре. Первые два были открыты И. Кеплером (1571 - 1630), а два других почти 200 лет спустя построил Л. Пуансо (1777 - 1859). Именно поэтому правильные звёздчатые многогранники называются телами Кеплера - Пуансо.
Все они получаются «озвездыванием» Платонова
т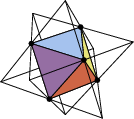 ела, то
есть продлением его граней до пересечения друг с другом, и потому
называются звездчатыми. Куб и тетраэдр не порождают новых фигур -
грани их, сколько ни продолжай, не пересекаются.
ела, то
есть продлением его граней до пересечения друг с другом, и потому
называются звездчатыми. Куб и тетраэдр не порождают новых фигур -
грани их, сколько ни продолжай, не пересекаются.
Если же продлить все грани октаэдра до
пересечения их друг с другом, то получится фигура, что возникает
при взаимопроникновении двух тетраэдров - «стелла октангула»,
которая называется «продолженным о ктаэдром».
ктаэдром».
Икосаэдр и додекаэдр дарят миру сразу четыре «почти правильных многогранника». Один из них - малый звездчатый додекаэдр, полученный впервые Иоганном Кеплером.
Столетиями математики не признавали за всякого
рода звездами права называться многоугольниками из-за того, что
стороны их пересекаются. Людвиг Шлефли не изгонял геометрическое
тело из семейства многогранников только за то, что его грани
самопересекаются, тем не менее, оставался непреклонным, как только
речь заходила про малый звездчатый додекаэдр. Довод его был прост и
весом: это кеплеровское животное не подчиняется формуле Эйлера! Его
колючки образованы д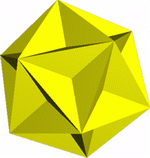 венадцатью
гранями, тридцатью ребрами и двенадцатью вершинами, и,
следовательно, В+Г-Р вовсе не равняется двойке.
венадцатью
гранями, тридцатью ребрами и двенадцатью вершинами, и,
следовательно, В+Г-Р вовсе не равняется двойке.
Ш лефли был
и прав, и не прав. Конечно же, геометрический ежик не настолько уж
колюч, чтобы восстать против непогрешимой формулы. Надо только не
считать, что он образован двенадцатью пересекающимися звездчатыми
гранями, а взглянуть на него как на простое, честное геометрическое
тело, составленное из 60 треугольников, имеющее 90 ребер и 32
вершины.
лефли был
и прав, и не прав. Конечно же, геометрический ежик не настолько уж
колюч, чтобы восстать против непогрешимой формулы. Надо только не
считать, что он образован двенадцатью пересекающимися звездчатыми
гранями, а взглянуть на него как на простое, честное геометрическое
тело, составленное из 60 треугольников, имеющее 90 ребер и 32
вершины.
Тогда В+Г-Р=32+60-90 равно, как и положено, но зато тогда к этому многограннику неприменимо слово «правильный» - ведь грани его теперь не равносторонние, а всего лишь равнобедренные треугольники. Кеплер не додумался, что у полученной им фигуры есть двойник.
М ногогранник,
который называется «большой додекаэдр» - построил французский
геометр Луи Пуансо спустя двести лет после кеплеровских звездчатых
фигур.
ногогранник,
который называется «большой додекаэдр» - построил французский
геометр Луи Пуансо спустя двести лет после кеплеровских звездчатых
фигур.
Большой икосаэдр был впервые описан Луи Пуансо в 1809 году. И опять Кеплер, увидев большой звездчатый додекаэдр, честь открытия второй фигуры оставил Луи Пуансо. Эти фигуры также наполовину подчиняются формуле Эйлера. [2]
Многогранники в искусстве
«Поистине, живопись - наука и законная дочь природы,
ибо она порождена природой»
(Леонардо да Винчи)
В эпоху Возрождения большой интерес к формам правильных многогранников проявили скульпторы, архитекторы, художники. Леонардо да Винчи (1452-1519) например, увлекался теорией многогранников и часто изображал их на своих полотнах. Он проиллюстрировал правильными и полуправильными многогранниками книгу Монаха Луки Пачоли «О божественной пропорции».
Знаменитый художник, увлекавшийся геометрией, Альбрехт Дюрер (1471-1528гг.), в известной гравюре «Меланхолия» на переднем плане изобразил додекаэдр.
Голландский художник Мориц Корнилис Эшер, родившийся в 1989 году в Леувардене, создал уникальные и очаровательные работы, в которых использованы или показаны широкий круг математических идей.
Правильные геометрические тела - многогранники - имели особое очарование для Эшера. В его многих работах многогранники являются главной фигурой и в еще большем количестве работ они встречаются в качестве вспомогательных элементов. На гравюре «Четыре тела» Эшер изобразил пересечение основных правильных многогранников, расположенных на одной оси симметрии, кроме этого многогранники выглядят полупрозрачными, и сквозь любой из них можно увидеть остальные.
Большое количество различных многогранников может быть получено объединением правильных многогранников, а также превращением многогранника в звезду. Для преобразования многогранника в звезду необходимо заменить каждую его грань пирамидой, основанием которой является грань многогранника.
Изящный пример звездчатого додекаэдра можно найти в работе «Порядок и хаос». В данном случае звездчатый многогранник помещен внутрь стеклянной сферы. Аскетичная красота этой конструкции контрастирует с беспорядочно разбросанным по столу мусором. Заметим также, что анализируя картину можно догадаться о природе источника света для всей композиции - это окно, которое отражается левой верхней частью сферы.
Фигуры, полученные объединением правильных многогранников, можно встретить во многих работах Эшера. Наиболее интересной среди них является гравюра «Звезды», на которой можно увидеть тела, полученные объединением тетраэдров, кубов и октаэдров. Если бы Эшер изобразил в данной работе лишь различные варианты многогранников, мы никогда бы не узнали о ней. Но он поместил внутрь центральной фигуры хамелеонов, чтобы затруднить восприятие всей фигуры. Таким образом, необходимо отвлечься от привычного восприятия картины и попытаться взглянуть на нее свежим взором, чтобы представить ее целиком. Этот аспект данной картины является еще одним предметом восхищения математиков творчеством Эшера. [2]
Многогранники в архитектуре
Наука геометрия возникла из практических задач, ее предложения выражают реальные факты и находят многочисленные применения.
Геометрия появляется всюду, где нужна хотя бы малейшая точность в определении формы и размеров.
Страна
Архитектурные сооружения
Геометрические
фигуры
Применение в современной
архитектуре
Древний Египет
Мастаба
Ступенчатая пирамида
( фараона Джосера)
Классическая пирамида
Погребальные комплексы
Храм богу Амону-Ра
Обелиск
Усеченная пирамида
Четырехугольная пирамида
Параллелепипед
Цилиндры
Пирамиды в Лувре, Франция, 20 в.
Мавзолей Ленина,
Россия 20 в.
-
высотных зданий
-
в Москве 20 в.
Башни «Петронас»
в Малайзии
Древняя Греция
Храм
Ордера
Параллелепипед
Призма
Цилиндр
Усеченный конус
Колоннада театров,
дворцов, парковых
ансамблей
Древний Рим
Триумфальные арки
Триумфальные колонны
Купол
Амфитеатр (Колизей)
Термы
Арки
Мосты
Параллелепипед
Цилиндр
Сфера
Триумфальные арки и колонны в Москве,
Санкт - Петербурге
Цирк
Стадион
Арочные мосты
Сауны и бани
Средние века
Замки-крепости
Параллелепипед
Пирамида
Конус
Усеченный конус
Цилиндр
Дома-коттеджи
Являются элементами жилых домов
Музей Плодов в Яманаши
Этот музейно-развлекательный комплекс, созданный с помощью трехмерного моделирования, продолжает тему музеев без произведений искусств.Как объясняет создатель Музея Ицуко Хасегава, одна из немногих преуспевающих японских женщин-архитекторов, "геометрия трех оболочек" была проанализирована с помощью объемных компьютерных построений. Каждая форма была образована путем вращения простых геометрических форм до получения сложных объемов.[2]

Многогранники в природе
Правильные многогранники - самые выгодные фигуры. И природа этим широко пользуется. Кристаллы некоторых знакомых нам веществ имеют форму правильных многогранников. Например, кристаллы поваренной соли имеют форму куба.
При производстве алюминия пользуются
алюминиево-калиевыми кварцами, монокристалл которых имеет форму
правильного октаэдра. Получение серной кислоты, железа, особых
сортов цемента не обходится без сернистого колчедана. Кристаллы
этого химического вещества имеют форму додекаэдра. В разных
химических реакциях применяется сурьменистый сернокислый натрий -
вещество, синтезированное учёными. Кристалл сурьменистого
сернокислого натрия имеет форму тетраэдра. Последний правильный
многогранник - икосаэдр передаёт форму кристаллов бора.
Алмаз (октаэдр)

Шеелит (пирамида)

Хрусталь (призма)

Поваренная соль (куб)
Звездчатые многогранники очень декоративны, что позволяет широко применять их в ювелирной промышленности при изготовлении всевозможных украшений. Применяются они и в архитектуре. Многие формы звездчатых многогранников подсказывает сама природа. Снежинки - это звездчатые многогранники. С древности люди пытались описать все возможные типы снежинок, составляли специальные атласы. Сейчас известно несколько тысяч различных типов снежинок.
П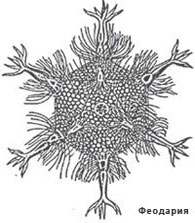 равильные
многогранники встречаются так же и в живой природе. Например,
скелет одноклеточного организма феодарии (Circjgjnia icosahtdra) по
форме напоминает икосаэдр. Большинство феодарий живут на морской
глубине и служат добычей коралловых рыбок. Но простейшее животное
защищает себя двенадцатью иглами, выходящими из 12 вершин скелета.
Оно больше похоже на звёздчатый многогранник. [2] Из всех
многогранников с тем же числом граней икосаэдр имеет наибольший
объём при наименьшей площади поверхности. Это свойство помогает
морскому организму преодолевать давление толщи воды.
равильные
многогранники встречаются так же и в живой природе. Например,
скелет одноклеточного организма феодарии (Circjgjnia icosahtdra) по
форме напоминает икосаэдр. Большинство феодарий живут на морской
глубине и служат добычей коралловых рыбок. Но простейшее животное
защищает себя двенадцатью иглами, выходящими из 12 вершин скелета.
Оно больше похоже на звёздчатый многогранник. [2] Из всех
многогранников с тем же числом граней икосаэдр имеет наибольший
объём при наименьшей площади поверхности. Это свойство помогает
морскому организму преодолевать давление толщи воды.
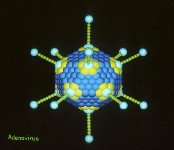
 Вирусы,
построенные только из нуклеиновой кислоты и белка, могут походить
на жесткую палочкообразную или гибкую нитевидную спираль, точнее на
правильный двадцатигранник, или икосаэдр. Есть вирусы,
размножающиеся в клетках животных (позвоночных и беспозвоночных),
другие облюбовали растения, третьи (их называют бактериофагами или
просто фагами) паразитируют в микробах, но икосаэдрическая форма
встречается у вирусов всех этих трех групп.
Вирусы,
построенные только из нуклеиновой кислоты и белка, могут походить
на жесткую палочкообразную или гибкую нитевидную спираль, точнее на
правильный двадцатигранник, или икосаэдр. Есть вирусы,
размножающиеся в клетках животных (позвоночных и беспозвоночных),
другие облюбовали растения, третьи (их называют бактериофагами или
просто фагами) паразитируют в микробах, но икосаэдрическая форма
встречается у вирусов всех этих трех групп.
Где еще можно увидеть эти удивительные тела? В очень красивой книге немецкого биолога начала нашего века Э. Геккеля "Красота форм в природе" можно прочитать такие строки: "Природа вскармливает на своем лоне неисчерпаемое количество удивительных созданий, которые по красоте и разнообразию далеко превосходят все созданные искусством человека формы". Cлайд№20
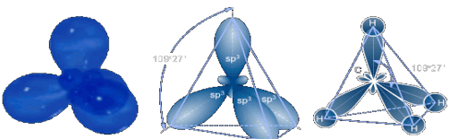
В молекуле метана, который удается очень точно измерить в эксперименте, а поскольку ни один атом водорода в молекуле СН4, очевидно, ничем не выделен, то разумно предположить, что эта молекула имеет форму правильного тетраэдра. Этот факт подтверждается фотографиями молекулы метана, полученными при помощи электронного микроскопа.
Идеи Пифагора, Платона, И. Кеплера о связи правильных
многогранников с гармоничным устройством мира уже в наше время
нашли свое продолжение в интересной научной гипотезе, авторами
которой (в начале 80-х годов) явились московские инженеры В.
Макаров и В. Морозов. Они считают, что ядро Земли имеет форму и
свойства растущего кристалла,
оказывающего воздействие на развитие всех природных процессов,
идущих на планете. Лучи этого кристалла, а точнее, его силовое
поле, обусловливают икосаэдро-додекаэдрическую структуру Земли ,
проявляющуюся в том, что в земной коре как бы проступают проекции
вписанных в земной шар правильных многогранников: икосаэдра и
додекаэдра.
Их 62 вершины и середины ребер, называемых авторами узлами, обладают рядом специфических свойств, позволяющих объяснить некоторые непонятные явления.
В трехмерном пространстве деления сферы ведут к созданию пяти правильных многогранников, так называемых пяти тел Платона. Формы Платона связаны с человеческим телом и природой сознания, раскрытие которой ведет не только к понимание интеллекта Вселенной, но и к эмпирическому восприятию Бога, даруя ощущение глубокой всеобщей взаимосвязи элементов бытия. Здесь особую роль играет число 5. Оно связано с зарождением жизни на земле и в то же время с бессмертием.
Первичные многоугольники и многогранники - фундаментальные образцы творения, представляющие творческие силы самоорганизации, которые формируют и определяют мир. Все в природе может быть описано в терминологии математических принципов, которые свойственны этим формам.
Какую форму могло бы иметь первое творение? Каковы изначально сотворенные объемные формы? Существует пять таких творений, которые являются наиболее существенными, потому что они - единственные тела, у которых все грани и все внутренние углы равны. Это тетраэдр, октаэдр, куб, додекаэдр и икосаэдр; производные от треугольника, квадрата и пятиугольника; воплощение чисел 3, 4 и 5. Все другие тела представляют собой только модификации эти пяти.
Заключение
Каков он, наш мир? Мы говорим: огромный, прекрасный, разнообразный…Мир, в котором мы живём, наполнен геометрией домов и улиц, гор и полей, творениями природы и человека. Если посмотреть вокруг, то можно заметить в обычных вещах такое, как что самая популярная форма современного здания, радиоприёмников, телевизоров, шкафов это-параллелепипед. Или в природе: цветах, бактериях, камнях и т.д. мы можем увидеть формы пространственных фигур. Эти формы фигур кажутся очень красивыми. Нас поражает красота, совершенство, гармония пространственных фигур.
Подбирая материал для своей работы, я познакомился с различными видами многогранников (правильные, неправильные, звездчатые) и их свойствами, узнал, где они встречаются в природе (кристаллы, соты, снежинки, феодария) и окружающем нас мире (головоломки, пирамиды, картины).
Решая поставленную проблему, я увидел, что многогранники окружают меня везде - это крупинки сахара и соли, камень в кольце мамы, форма зданий и деревьев и многое другое. Гармония между красотой и многогранностью существует.
Эта работа была для меня интересна. Думаю, что собранный материал будет полезен мне и моим одноклассникам.
Список использованной литературы
-
Атанасян Л.С.. Бутузов В.Ф. Геометрия 10-11; М. ; «Просвещение». 2000.
-
Интернет сайт www.уаndeх.ru
3 . Крайнева Л.Б. Построение правильных многогранников с использованием куба //Математика в школе.-1994.-2.-54-57
4. Смирнова И.М. Учебное пособие для10-11 классов гуманитарного профиля; «Просвещение» 1997.
5. Смирнова И.М. Уроки стереометрии в гуманитарных классах. Изучение многогранников//Математика в школе.-1934.- 4 .-41-47
Приложение 1
Архитектурные сооружения Древнего Египта, Древней Греции
 «Ложная
пирамида» Снефру
«Ложная
пирамида» Снефру

Пирамида Хефрена

Ступенчатая пирамида фараона Джосера
Приложение 2
Ф
ото архитектурных сооружений города Лесосибирска


Приложение 3
Многогранники в деталях автомобиля

двигатель
капот 
Приложение 4
Модели для изготовления многогранников
у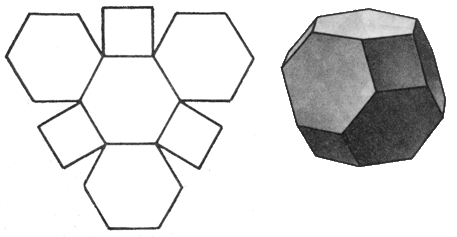
сеченный октаэдр
Октаэдр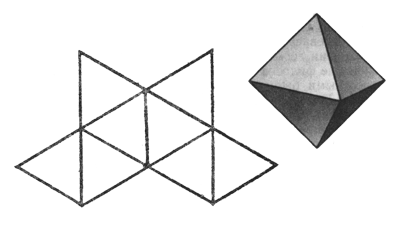
т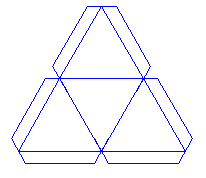
етраэдр
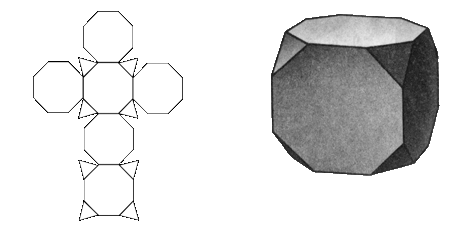
</ усеченный гексаэдр