- Учителю
- 'Функция мәндерінің жиынын табу' ҰБТ есептері
'Функция мәндерінің жиынын табу' ҰБТ есептері
ҰБТ есептері
Функция мәндерінің жиынын табу
Тайжанова Қ
Функция мәндерінің жиынын табу
Функция мәндерінің жиынын табу көп жағдайда теңдеудің шешімін табумен байланысты болады. ![]() саны f функциясының мәндер жиынына кіру үшін
саны f функциясының мәндер жиынына кіру үшін ![]() = f (x) теңдеуінің x
= f (x) теңдеуінің x ![]() шешімінің болуы қажетті және жеткілікті. Бұл теңдеудің
шешімінің болуы қажетті және жеткілікті. Бұл теңдеудің ![]() - дің мәніне байланысты бір түбірі, бірнеше түбірі немесе түбірі болмауы да мүмкін.
- дің мәніне байланысты бір түбірі, бірнеше түбірі немесе түбірі болмауы да мүмкін.
Функция мәндерінің жиынын табуда әртүрлі тәсілдерді қолдануға болады.
-
Параметр енгізу арқылы ;
-
Берілген функцияның E (y) мәндері облысын кері ф - ң D (x) анықталу облысымен алмастыру ;
-
Квадраттық ф - ң қасиетін пайдалану ;
-
Сыртқы ф - ң монотондылық қасиетін пайдалану ;
-
Туынды көмегімен ;
-
Бағалау әдісі арқылы ;
-
Тікелей есептеу арқылы ;
-
Графиктік әдіс арқылы ;
-
Ақиқат теңсіздіктер көмегімен .
№ 1 есеп. Квадраттық функцияның қасиетін пайдалану
y= a![]() + bx + c Парабола төбесінің координатасын табу, онда m = -
+ bx + c Парабола төбесінің координатасын табу, онда m = - ![]() , n = -
, n = - ![]()
Егер а ![]() 0 болса, онда E (y) =
0 болса, онда E (y) = 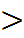 ; +
; + ![]() ,
,
ал а ![]() болса, онда E (y) = ( -
болса, онда E (y) = ( - 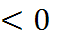
y = ![]() - 2x + 10 E (y) - ?
- 2x + 10 E (y) - ?
n = - ![]() = -
= - 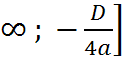 = 9
= 9
а ![]() 0 E (y) =
0 E (y) = ![]() .
.
№ 2 Бағалау әдісі
-
1
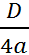
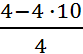
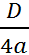 1
1 -
1
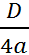
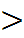 1
1 -
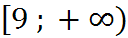
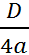 arc
arc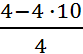
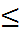
0 ![]() arc
arc![]()
![]()
![]()
-
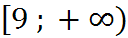
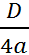 arctg x
arctg x 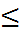
0 ![]() arcctg x
arcctg x ![]()
![]()
![]() 0
0
![]()
![]() 0, n
0, n ![]() N
N
![]()
![]() 0
0
![]()
![]() 0, n
0, n ![]() N
N
y= ![]() - 2
- 2
![]() - 2 =
- 2 = ![]()
![]() =
= ![]() + 2
+ 2
![]()
![]() 0 б / тан,
0 б / тан, ![]() + 2
+ 2 ![]() 0 болу керек.
0 болу керек.
![]()
![]() - 2
- 2
E (y) = (-2 ; + ![]() ) .
) .
№ 3
y= ![]() E (y) - ?
E (y) - ?
Анықталу облысы
![]()
![]() 0
0 ![]()
![]() 0, онда E (y) =
0, онда E (y) = ![]() .
.
№ 4
y=1 - (![]() E (y) - ?
E (y) - ?
(![]()
![]() 0 - (
0 - (![]()
![]() 0 1 - (
0 1 - (![]()
![]() 1
1
E (y) = (- ![]() )
)
№ 5
Туынды көмегімен мәндер жиынын табу.
y=![]() +
+ ![]() E (y) - ?
E (y) - ?
Шешуі : фун - ң анықталу облысын табамыз
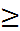
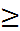
x + 4 ![]() 0 x
0 x![]() - 4
- 4
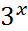
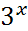
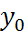
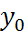
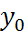
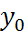
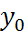
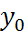
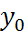
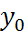
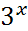
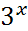
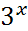
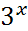
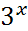
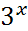
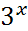
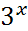
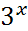
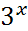
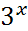
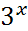
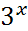 2 - x
2 - x ![]() 0 x
0 x ![]() 2
2
4 2
![]() 4
4 ![]() x
x ![]() 2 осы аралықтағы фун - ң ең үлкен, ең кіші мәнін табамыз
2 осы аралықтағы фун - ң ең үлкен, ең кіші мәнін табамыз
y![]() =
= ![]()
![]()
![]() =
= 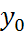
Кризистік нүктесін табу
y![]() = 0
= 0 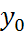 = 0
= 0
![]() -
- ![]() = 0
= 0
![]() =
= ![]()
2 - x = x + 4
2x = - 2
x = - 1 ![]() D (y)
D (y)
y(- 4) = ![]() +
+ ![]() =
= ![]()
y(-1) = ![]() +
+ ![]() =
= ![]() +
+ ![]() = 2
= 2![]()
y(2) = ![]() +
+ ![]() =
= ![]()
Ең үлкен мәні 2![]() , ең кіші мәні
, ең кіші мәні ![]()
E (y) = ![]()
№ 6
y = arc![]() + 3 E (y) - ?
+ 3 E (y) - ?
![]()
![]() arc
arc![]()
![]() 3 - ті қосамыз
3 - ті қосамыз
![]()
![]() arc
arc![]() + 3
+ 3 ![]() + 3
+ 3
E (y) = 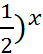
№ 7
f (x) = ![]()
E (y) ; ![]() = a x - 2 =
= a x - 2 = ![]() x =
x = ![]() + 2
+ 2
x = 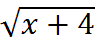 a
a ![]() 0
0
Жауабы : (- ![]() )
) ![]() (0; +
(0; + ![]() )
)
№ 8
y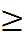
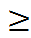 = a
= a
x = ax + a
x - ax = a
x (1 - a) = a
x = ![]()
E (y) = (- ![]() )
) ![]() (1; +
(1; + ![]() )
)
№ 9
y= 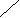
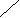 = a
= a
![]() + 1 = ax
+ 1 = ax
![]() - ax + 1 = 0
- ax + 1 = 0
D = ![]() - 4
- 4 ![]() 0
0
(a - 2) (a + 2) ![]() 0
0
+ - +
 -2 2
-2 2
E (y) = ( - ![]()
![]()
![]()
№ 10
f (x) = 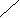
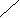 = a
= a
x = ![]() + a
+ a
![]() + a = 0
+ a = 0
D = 1 - 4 ![]()
![]() 0
0
(1 - 2a) (1 + 2a) ![]() 0
0
- + -
 -
-![]()
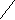
Жауабы :
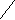
№ 11
f(x) = ![]() +
+ ![]()
![]() =
=
көмекші бұрыштарды пайдаланамыз
= 2 (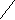 ) = 2
) = 2 ![]() (
(![]() )
)
![]()
![]() =
= ![]()
![]()
![]() =
= ![]()
![]()
![]()
![]()
![]() 1
1
![]()
![]()
![]() 2
2
E(y) = ![]()
№ 12
y =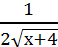 x =
x =
![]() +1 =
+1 = ![]()
![]() =
= ![]() - 1
- 1
![]() =
= ![]()
y =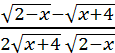
![]()
![]() 0
0
![]()
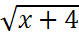 0 2
0 2
Жауабы : E(y) = (0; ![]()
№ 13
f(x) = 6 ![]()
туынды көмегімен шығару
f(x) = 6 ![]() = 2 cos2x - 1 + 6
= 2 cos2x - 1 + 6![]() =
=
= 2 cos2x + 6![]() - 1
- 1
![]() = t
= t
![]()
![]() 1 болғандықтан t
1 болғандықтан t ![]()
![]()
g (t) = 2![]() + 6t - 1 ф - ң
+ 6t - 1 ф - ң ![]() аралығындағы ең үлкен, ең кіші мәндерін табайық.
аралығындағы ең үлкен, ең кіші мәндерін табайық.
Төбесі жоғары қараған парабола
m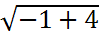 = -
= - ![]() = -
= - ![]() = -
= - ![]()
![]()
![]()
g (-1) = 2 - 6 - 1 = - 5
g (1) = 2 + 6 - 1 = 7
ең үлкен мән : 7, ең кіші мән : - 5
Жауабы : ![]()
№ 14
f(x) = 2![]() + cos2x E(y) - ?
+ cos2x E(y) - ?
f(x) = 2![]() + cos2x = 2
+ cos2x = 2![]() + 1 - sin2x
+ 1 - sin2x
![]() = t
= t
![]()
m = - ![]() =
= 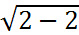 = 1 1
= 1 1 ![]()
![]()
g (-1) = ![]()
g (1) = ![]()
E(y) = ![]()
№ 15
y =![]()
![]()
![]() 0
0
![]()
![]() 0
0
![]()
![]() 0
0
E(y) = (0; + ![]() )
)
№ 16
y= ![]() =
= ![]()
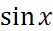
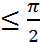
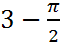
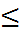 y y=
y y=![]()
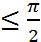 y=
y=![]()
1
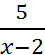
![]()
-1 1 x
Жауабы : 
№ 17 y
17 y
y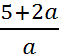
 = -
= - ![]() = -
= - ![]() 1 y=-
1 y=-![]()
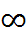
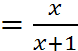 x
x
![]() 1
1
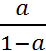 y=-
y=-![]()
x
-1
0
1
y
-1
-![]()
-1
E(y) = (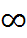
№ 18
Ақиқат теңсіздіктер көмегімен
(Коши теңсіздігі арқылы)
f(x) = ![]() +
+ ![]()
![]()
![]()
![]() a,b
a,b ![]() (Коши теңсіздігі)
(Коши теңсіздігі)
![]()
![]() 0 болғандықтан
0 болғандықтан ![]() +
+ ![]()
![]() 2
2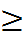 = 6
= 6
![]() +
+ ![]()
![]() 6
6
E(y) = ![]()
Қызылорда облысы
Қармақшы ауданы
Ақжар ауылы
№ 28 орта мектептің математика пәнінің мұғалімі Тайжанова Қалдыгүл