Урок по математике (алгебра) для 8 класса по теме «Квадратные уравнения»

Многоуровневая система математических задач, проектирование и использование в условиях профильного обучения»

Выполнила

учитель математики

МБУ лицея № 6

г.о. Тольятти

Корнилова Любовь

Александровна

Тольятти - 2013

Пояснительная записка

Главной целью работы учителя является повышение уровня знаний учащихся, развитие у них аналитического и логического мышления с перспективой применения их в дальнейшей практической деятельности, и воспитание в конечном итоге конкурентоспособного выпускника.

Одним из методов обучения решению задач является многоуровневый метод. Основной принцип работы заключается в разделении метода обучения на три основных уровня: ЗЗ ( знакомая задача), МЗ (модернизированная задача) и НЗ (незнакомая) задача.

На первом уровне обучения решению задач учителем подбирается условие типовой задачи. Первый уровень обучения, как правило, предполагает обучение решению задач, содержащих в своём решении одно или два действия.

Второй уровень обучения решению задач отличается тем, что задачи модернизированные. При закреплении задач, обучение решению которых соответствует второй уровень, может быть предложена задача с другим условием, отличным от первоначального.

На третьем уровне обучения предложены задачи нетиповые, которые имеют как правило несколько решений.

Выработка данных навыков в решении задач должна приучить учащихся, как в учебной, так и в дальнейшей профессиональной деятельности проводить предварительный анализ предстоящей работы, строить её по рациональному плану, определив предварительно этапы работы, порядок их выполнения, необходимые элементы и материалы.

Многоуровневый метод позволяет повысить уровень мышления отстающих учащихся и научить их самостоятельно решать любые задачи.

Безусловно, учитель играет ведущую роль в формировании УУД. Подбор содержания, разработка конкретного набора наиболее эффективных учебных заданий (в рамках каждой предметной области), определение планируемых результатов - всё это требует от педагога грамотного подхода.

Перечень базовых задач

1. Определение квадратного уравнения

2. Неполные квадратные уравнения

3. Решение квадратного уравнения по формуле

4. Решение квадратного уравнения с четным вторым коэффициентом

5. Теорема Виета

6. Решение дробных рациональных уравнений

7. Решение уравнений сводящихся к квадратным

Тема «Квадратные уравнения»

8 класс

№ п/п

Название задачи

Тип задачи

Содержание задачи

Задания

(Алгебра, 8 класс,

Автор Мордкович А. Г.)

1

Определение квадратного уравнения

ЗЗ

Преобразуйте уравнение к виду ax²+bx+c=0 и укажите старший коэффициент, второй коэффициент и свободный член

№24.2 - 24.6

МЗ

Составьте квадратное уравнение

№24.7, №24.8, №24.13

НЗ

При каких значениях а уравнение является квадратным?

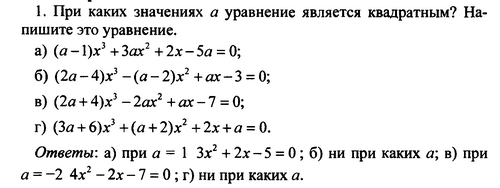
2

Неполные квадратные уравнения

ЗЗ

Решите уравнение:

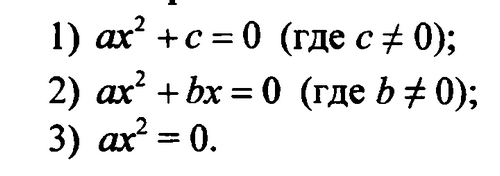
№24.16 - №24.20

МЗ

Решить неполное уравнение

№24.21 - №24.22

НЗ

Решить неполное уравнение с параметром

№24.31 - №24.32

3

Решение квадратного уравнения по формуле

ЗЗ

Решите уравнение

№25.5 - №25.19

МЗ

Решить квадратное уравнение

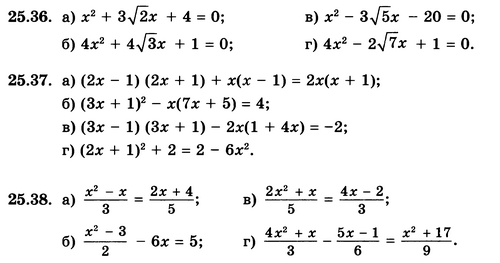
НЗ

Решить квадратное уравнение с параметром

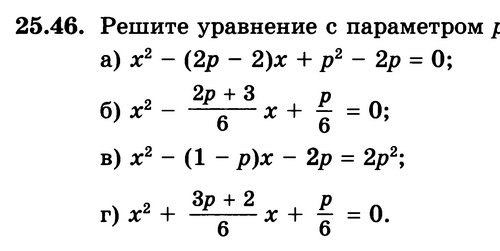
4

Решение квадратного уравнения с четным вторым коэффициентом

ЗЗ

Решите уравнение

с четным вторым коэффициентом

№28.1 - №28.6

МЗ

Решить квадратное уравнение

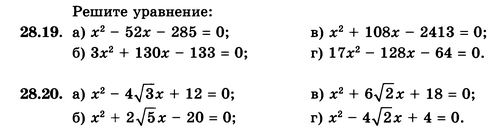
НЗ

Решить квадратное уравнение с параметром

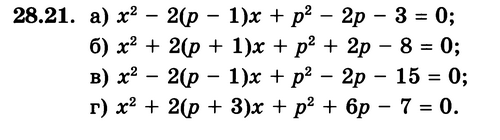
5

Теорема Виета

ЗЗ

Найдите сумму и произведение корней квадратного уравнения

№29.2 - №29.5

МЗ

Не используя формулу корней, найти корни квадратного уравнения

№29.6 - №29.8

НЗ

Использование теоремы Виета при решении различных упражнений

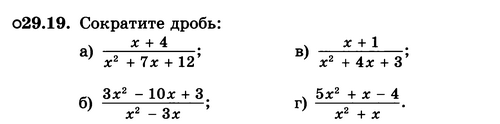
6

Решение дробных рациональных уравнений

ЗЗ

Найдите корни уравнения

№26.1 - №26.5

МЗ

Решение упражнений, приводящих к составлению дробного рационального уравнения

НЗ

Решение более сложных дробных рациональных уравнений

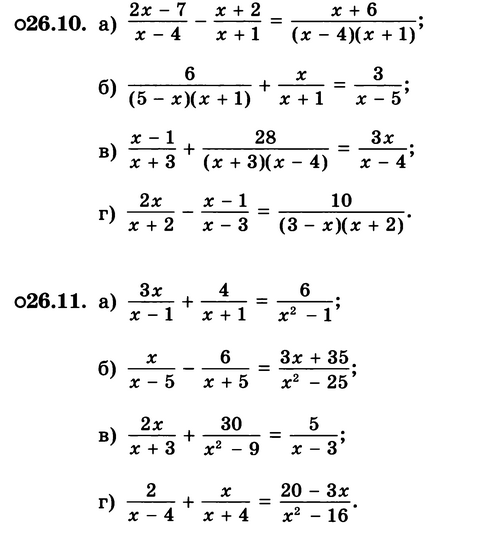
7

Решение уравнений сводящихся к квадратным

ЗЗ

Биквадратные уравнения

МЗ

Уравнения с модулем

НЗ

Иррациональные уравнения

№30.1 - №30.4, 30.11 - №30.13

Литература:

1. Алгебра. Сборник рабочих программ. 7-9 классы: пособие для учителей общеобразоват. учреждений-(сост. Т. А. Бурмистрова) - М.: Просвещение, 2011.

2. Учебник Мордкович А. Г. . Алгебра 8 класс. М.: Мнемозина, 2012

3. «Сборник заданий для подготовки к итоговой аттестации в 9 классе». Авторы: Л.В. Кузнецова и другие.

4. «Дидактические материалы по алгебре для 8 класса».

Автор Л. А. Александрова. М.: Мнемозина, 2012

5. «Галицкий М.Л., Гольдман А.М., Звавич Л.И., Сборник задач по алгебре для 8-9 классов. М.: Просвещение, 2008