Урок по алгебре для 11 класса «Понятие корня n-й степени из действительного числа»

Технологическая карта урока-консультации по теме: «Понятие корня n-й степени из действительного числа»

(по А.Г.Мордковичу, 11 класс)

Тип урока: Урок открытия нового знания

Цель: систематизировать знания учащихся по теме «Понятие корня n-й степени из действительного числа»

Формы работы: индивидуальная, работа в парах, фронтальная

За несколько дней до урока-консультации учащимся дается задание самостоятельно изучить тему: «Понятие корня n-й степени из действительного числа» стр. 200-204 и составить план-конспект, ориентируясь на следующие вопросы.

Теоретические вопросы:

1. Корень n-й степени из неотрицательного числа а. Извлечение корня.

2. Количество корней уравнения xⁿ = a при n - четном и n - нечетном

3. Корень нечетной степени n из отрицательного числа а. Извлечение корня.

Практические вопросы:

Задачи №№4.6-4.8(а, б), 4.10-4.11(а, б)

Ученик в процессе выполнения предложенных учителем заданий составляет вопросы, в которых не смог разобраться, фиксирует те задачи, которые не смог решить, записывает их и отдает учителю за день до урока-консультации. На основе этих вопросов учитель планирует урок-консультацию.

Этапы урока

Деятельность учителя

Деятельность учащихся

Формируемые УУД

1. Самоопределение к учебной деятельности

Цели: 1) включить учащихся в учебную деятельность;

2) сформулировать цель урока.

Выясняет на сколько учащиеся усвоили тему для самостоятельного изучения: какие вопросы возникли при написании конспекта; что вызвало затруднение.

Предлагает каждому учащемуся, исходя из трудностей, с которыми каждый столкнулся сформулировать для себя цель, которую хотели бы достичь к концу урока.

Отмечают трудности, с которыми столкнулись при написании конспекта и решении задач.

Формулирует цель и фиксируют у себя в тетради.

Л: самоопределение

П: построение речевого высказывания; формулирование цели.

Р: целеполагание.

К: планирование учебного сотрудничества

2. Актуализация знаний и фиксация затруднений

Цели: 1) актуализировать учебное содержание, необходимое для восприятия нового материала: графическое решение уравнений вида х² = а, х³ = а; извлечение квадратного и кубического корней; а также мыслительные операции, необходимые для восприятия нового материала: сравнение, аналогия, анализ, обобщение;

3) зафиксировать все повторяемые понятия в таблицу 1;

4) зафиксировать индивидуальные затруднения в деятельности, демонстрирующее недостаточность имеющихся знаний: нахождение корней уравнения xⁿ = a при n - четном и n- нечетном

Решите графически уравнения х² = 4, х³ = 8, х⁴ = 5, х⁵ = 5. Результаты решения занесите в таблицу 1

Что у вас вызвало затруднение?

Пытаются самостоятельно выполнить индивидуальное задание на актуализацию старых знаний и применение нового знания: заполняют таблицу 1, результаты выносят на доску.

Фиксируют возникшее затруднение при нахождении корней уравнения х⁴ = 5, х⁵ = 5

П: анализ, сравнение, аналогия, подведение под понятие, представление информации в графическом и табличном виде.

Р: выполнение пробного учебного действия; фиксация индивидуального затруднения; волевая саморегуляция в ситуации затруднения.

3. Выявление места и причины затруднения

Цель: организовать коммуникативное взаимодействие, в ходе которого выявляется и фиксируется задание, вызвавшее затруднение в учебной деятельности

Почему именно в этих уравнениях не получается найти корни? Чем они отличаются от предыдущих двух?

Сравнивают решения уравнений и делают вывод о том, что в отличие от уравнений х² = 4, х³ = 8 в уравнениях х⁴ = 5, х⁵ = 5 нельзя подобрать такое число, которое при возведении в 4-ю и 5-ю степень дает число 5.

П: анализ, сравнение, аналогия, подведение под понятие, постановка и формулирование проблемы, построение речевого высказывания

Р: волевая саморегуляция в ситуации затруднения

К: выражение своих мыслей; аргументация своего мнения.

4. Построение проекта выхода из затруднения

Цели: 1) организовать коммуникативное взаимодействие для построения нового способа действия, устраняющего причину выявленного затруднения;

2) зафиксировать новый способ действия в знаковой, вербальной форме и с помощью эталона.

Предлагает учащимся, справившимся с этим заданием, объяснить, как можно записать корни уравнения, проследить аналогию с предыдущими решениями.

Сформулируйте определение корня n-й степени из неотрицательного числа а и на основании результатов таблицы, сделайте вывод о количестве корней уравнения xⁿ = a при n - четном и n- нечетном

Два ученика по очереди выходят к доске, заполняют две последние строки таблицы, объясняя каждое выполненное действие.

Прослеживают аналогию при решении уравнений

х² = 4

х³

= 8

х⁴ = 5

х⁵ = 5

х =

х = 2

Не извл.

Не извл.

Формулируют определение: корнем n-й степени из неотрицательного числа а называется такое неотрицательное число, при возведении которого в степень n получается а. Это число обозначают , число а называют подкоренным числом, n - показателем корня

Сравнивая результаты, полученные в третьем столбце таблицы 3, делают вывод о том, что при n - четном уравнения xⁿ = a имеет два корня при n- нечетном один корень .

П: анализ, синтез, обобщение, аналогия, поиск и выделение необходимой информации; выдвижение гипотез и их обоснование; построение логической цепи рассуждений; создание способа решения проблемы.

Р: волевая саморегуляция в ситуации затруднения

К: выражение своих мыслей; аргументация своего мнения; учет разных мнений.

5. Первичное закрепление во внешней речи

Цель: зафиксировать изученное учебное содержание во внешней речи.

Заполните таблицу 2 по образцу, данному в первой строке (приложение 1).

Организовывает работу в парах: 1-й ученик выполняет №4.6(в), 4.8(в), 2-й ученик выполняет №4.6(г), 4.8(г). Затем объясните друг другу решение своих заданий.

Заполняют таблицу 2, проговаривают по очереди ответы.

Выполняют задания индивидуально, затем работают в парах: по очереди комментируют решения своих заданий, в случае затруднений помогают друг другу справиться с заданием, исправить ошибки.

П: выполнение действия по алгоритму; построение логической цепи рассуждений; обобщение; подведение под понятие.

К: выражение своих мыслей; достижение договоренности и согласование общего решения

6. Самостоятельная работа с проверкой по эталону.

Цель: проверить умение извлекать корень n-й степени, а также представлять информацию в виде схемы.

По аналогии с определением корня n-й степени из неотрицательного числа а, сформулируйте определение корня нечетной степени n из числа а и заполните схему:

Корень n-й степени

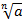
Если а ≥ 0, n = 2, 3, 4, 5, …, то

Если а < 0, n = 3, 5, 7,…, то

Самостоятельно решите №4.10(в, г), 4.11 (в, г). Признак того, что вы закончили работу - поднятая рука. Получите ключ для самопроверки.

Формулируют определение: корнем нечетной степени n из числа а называют такое отрицательное число, при возведении которого в степень n получается а. Заполняют схему, результаты выносят на доску:

Корень n-й степени

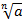
Если а ≥ 0, n = 2, 3, 4, 5, …, то

Если а < 0, n = 3, 5, 7,…, то

Решают номера. После выполнения работы учащиеся проверяют свои ответы и отмечают правильно решенные примеры, анализируют и исправляют допущенные ошибки.

П: анализ, синтез, аналогия, классификация, подведение под понятие; построение речевого высказывания; выполнение действий по алгоритму.

Р: контроль, коррекция, самооценка.

7. Рефлексия деятельности на уроке

Цели: 1) оценить свою деятельность на уроке;

2) проверить достижение поставленной цели;

3) обсудить и записать домашнее задание.

- Какую цель вы поставили в начале урока?

- Достигли ли вы своей цели?

- Что вам помогло справиться с затруднениями, возникшими дома?

- Оцените свою работу на уроке?

Постановка д/з: еще раз посмотрите №№4.6-4.8(а, б), 4.10-4.11(а, б). Какие ошибки были допущены при решении. Выполните эти задания, если не смогли справиться с ними до урока-консультации.

Несколько учащихся по очереди проговаривают свою цель и отмечают на сколько достигли ее к концу урока, со всеми ли трудностями смогли справиться. Анализируют и оценивают свою работу на уроке.

Записывают домашнее задание.

Р: рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности, адекватное понимание причин успеха и неуспеха.

К: выражение своих мыслей; аргументация своего мнения

Рабочие таблицы к уроку

Таблица 3

Уравнение

Геометрическая иллюстрация

Количество корней уравнения

Корни уравнения

х² = 4

х³ = 8

х⁴ = 5

х⁵ = 5

Таблица 4

Возведение в степень

Извлечение корня

5²

25

5

8

2

0,4⁴