Сценарий урока по геометрии

Муниципальное общеобразовательное учреждение Красноярская средняя школа

Урок по геометрии , 11 класс

Учебник А.С. Атанасяна

Учитель высшей категории Макарова Т.Д.

Тема « Векторы. Метод координат в пространстве »

Цель урока:

Обобщить и систематизировать знания и навыки решения задач учащихся по данной теме

Задачи урока:

• Обучающие: систематизировать знания учащихся по теме

• Развивающие: развивать навыки самостоятельной работы при работе на ПК

• Воспитательные: воспитание культуры оформления задач и умения работать с ПК

Ход урока.

- Сегодня у нас заключительный урок по теме «Векторы. Метод координат в пространстве ». Это зачетный урок, на котором мы должны повторить основные определения и формулы по данной теме, выполнить тест и решить индивидуальные задачи.

Итак, план нашего урока.

1. Устная работа на основные определения и формулы, необходимые при выполнении теста - минимум обязательных знаний и умений по данной теме (составление шифра)

2. Решение тренировочных задач (использование мультипроектора, диск « Геометрия 10-11 класс»)

3. Тест - зачет с индивидуальным использованием ПК

4. Решение разноуровневых задач

5. Итоги урока

1. Устная работа (составление шифра с использованием презентации).

- ? Дать определение вектора в пространстве.

- ? Как обозначается вектор в пространстве.

Задание 1. На каком из рисунков правильное изображение вектора?

А Б В Г

a

C

СD

- Вектор характеризуется двумя величинами: длиной (модулем) и направлением. Поговорим о каждой из данных характеристик вектора.

Задание 2. Среди предложенных формул укажите формулу нахождения длины вектора, если известны координаты его начала и конца А(х₁;у_1,z₁) и В (х₂;у_2,z₂)

А) |АВ|=

Б) |АВ|=

В) |АВ|=

Г) |АВ|=

- Рассматривая векторы в пространстве, мы выделяем понятие коллинеарности векторов.

- ? Какие вектора называются коллинеарными?

- ? На какие две группы они делятся?

Задание 3. Как установить коллинеарность векторов через их координаты?

Выберите верное утверждение.

Векторы и коллинеарные, если

А) их соответствующие координаты равны: х₁ = х₂; у₁ = у₂ , z₁=z₂

Б) их соответствующие координаты противоположны: х₁ = -х₂; у₁= -у₂; z₁ = -z₂

В) их соответствующие координаты пропорциональны: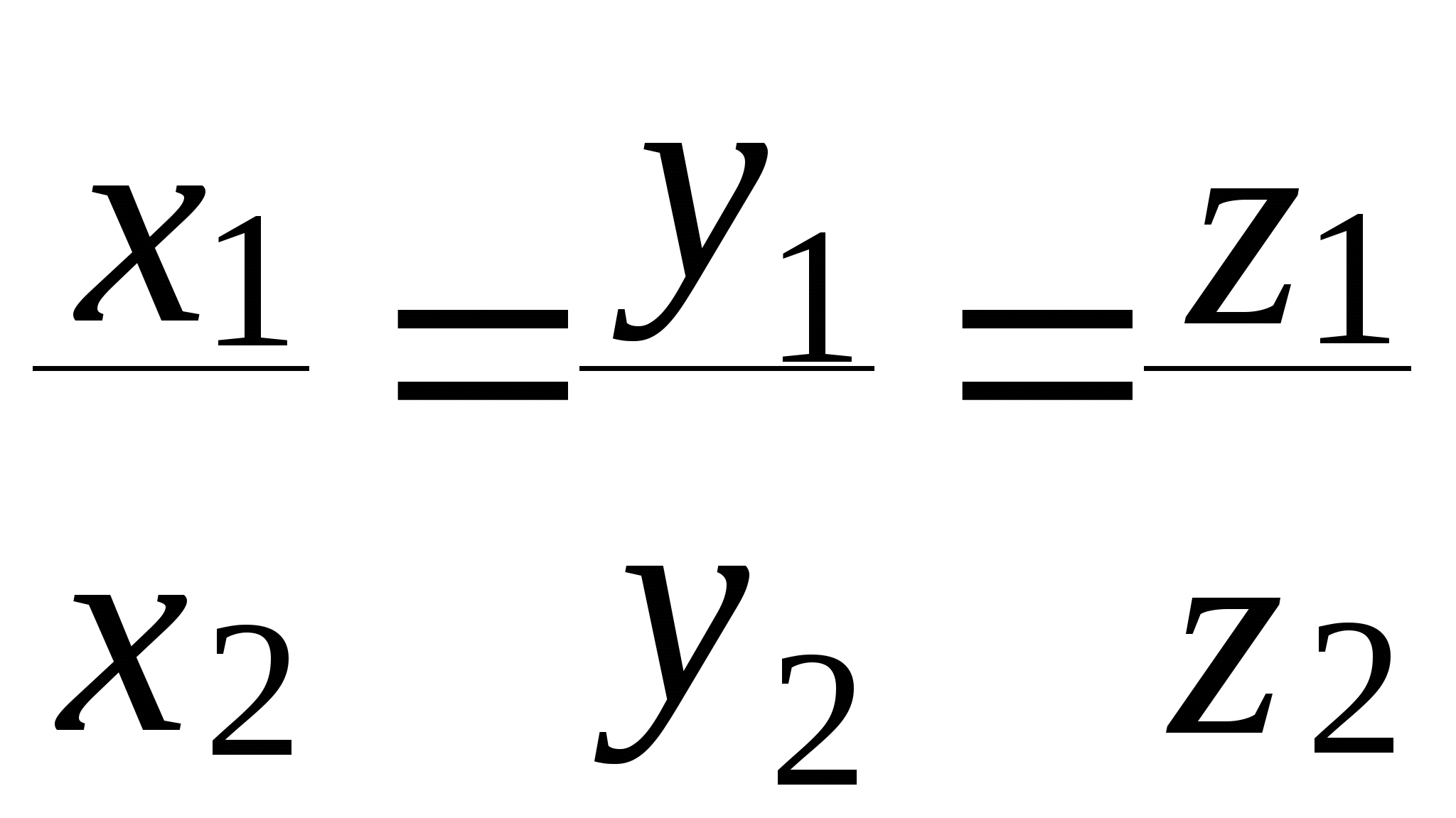

Г) сумма произведений соответствующих координат равна нулю: х₁х₂+у₁у₂+z₁z₂=0

Задание 4. Выясните, какой угол образуют вектора и , если их скалярное произведение =5

А) острый Б) прямой В) тупой Г) развернутый

Задание 5. Какое из данных утверждений неверно:

А)

Б)

В)

Г)

На доске выписываются некоторые шифры учащихся, сверяются с правильным кодом, выясняются вопросы, по которым допущены ошибки.

2. Решение тренировочных задач.

Решение задач на повторение основных формул и методов решения задач по данной теме с использованием CD «Геометрия 10-11»

(раздел - задачи; тема - векторы в пространстве; задачи № 4.5.6.10; воспроизвести - звук- до решения)

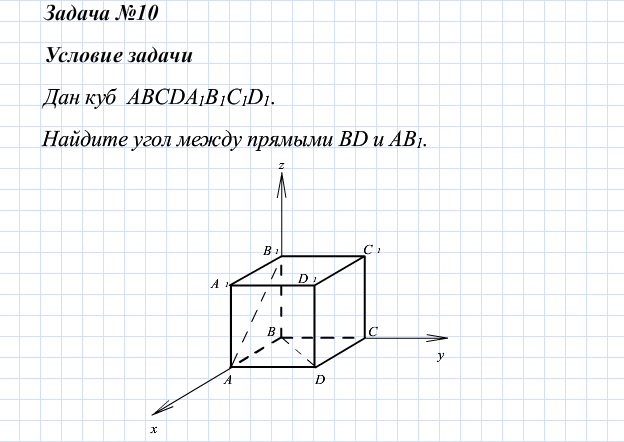
Условия задач для учащихся зачитываются компьютером, решение выполняется на доске для всего класса.

Для задачи №10 можно предложить учащимся найти другое решение задачи.

3. Тест - зачет индивидуально выполняется каждым учащимся класса на компьютере; при выполнении теста звучит музыка; см. приложение Test!\mytest.exe</</u>F11t-01(1).tst F11t-01(2).tst

- При выполнении всех заданий компьютер оценит ваши знания по данной теме, выставив вам оценку. Получив отметку, поднимаем руку, чтобы учитель зафиксировал ее в журнале. И, исходя из полученной оценки и реально оценивая свои знания, выбираем задачи разного уровня для индивидуального выполнения (можно работать в классе или для домашней работы).

В каждом задании указан сайт для индивидуальных решений

упражнений

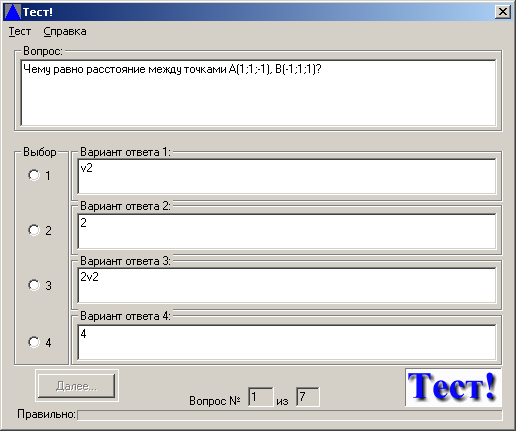
Тест №1.вариант 2. Геометрия,11 класс

Чему равно расстояние между точками А (-1;1;-1), В(-1;1;1)?

v2

2

2v2

4

Какая из указанных точек М является серединой отрезка АВ, где А(-1;-1;1), В(1;-1;-1)?

М(0;-2;0)

М(0;2;0)

М(0;-1;0)

М(0;1;0)

Какая из указанных точек М является проекцией точки А(2;3;6) на плоскость Оzу?

М(2;0;0)

М(0;3;0)

М(0;3;6)

М(2;0;6)

Даны точки А(-1;0;1) и В(1;-1;0). Чему равны координаты вектора ВА?

(0;-1;1)

(2;-1;-1)

(-2;1;1)

(2;1;1)

При каких значениях m векторы а (-1;1; m) и b (-1;1;2m) коллинеарны?

Ни при каких

При m=2

При m=1

При m=-1

4. Индивидуальное решение разноуровневых задач

(выбор домашнего задания)

« Незнакомые задачи»

( «5»)

www.school-tests.ru/online-math_10_11.html

• Найдите координаты вектора 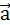, коллинеарного вектору 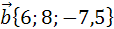и образующим тупой угол с координатным вектором 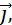если

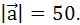
• Дана правильная треугольная призма АВСА₁В₁С₁ , в которой АА₁ =√2АВ. Найдите угол между прямыми АС₁ и А₁В.

« Малознакомые задачи»

«4»

www.school-tests.ru/online-math_10_11.html

• В кубе ABCDA₁B₁C₁D₁ точка М лежит на ребре BB₁, причем ВМ: МB₁=3: 2, а точка N лежит на ребре АD, причем AN: ND=2: 3. Вычислите косинус угла между прямыми MN и AB.

• Точки А(1;1;5), В(4;7;5),С(8;5;5),D(5;-1;5) являются вершинами прямоугольника АВСD. Найдите косинус большего угла между диагоналями прямоугольника.

« Знакомые задачи»

«3»

www.school-tests.ru/online-math_10_11.html

Вычислите косинус между прямыми АВ и СD, если А(1;1;0),

В(3;-1;0), С(4;-1;2), D(0;1;0).

5. Итоги урока.

Отметить основные этапы изученного материала,

выставление оценок.