Задания 17 для подготовки к ЕГЭ профильного уровня.

Вариант 10

Задание 17. В июле планируется взять кредит в банке на сумму 16 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:

- каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;

- с февраля по июнь каждого года необходимо выплатить часть долга;

- в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.

На сколько лет планируется взять кредит, если известно, что общая сумма выплат после его полного погашения составит 38 млн рублей?

Решение.

Взятый в первый год кредит в сумме 16 млн рублей, на следующий год сначала увеличивается на 25%, т.е. становится равный млн рублей, а затем, идет погашение таким образом, чтобы выплаты были равными каждый год. Предположим, что долг выплачивается лет, тогда после первого года выплата составит и сумма долга будет равна

млн рублей.

После второго года следует сделать выплату в размере и сумма долга будет равна

.

Таким образом, после лет сумма долга будет равна

,

а размер выплат составит

или в виде

,

так как по условию задачи общая сумма выплат составила 38 млн рублей. Учитывая, что

,

получим

То есть на 10 лет.

Ответ: 10.

Вариант 7

Задание 17. 15 января планируется взять кредит в банке на 19 месяцев. Условия его возврата таковы:

- 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца;

- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

- 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.

Известно, что общая сумма выплат после полного погашения кредита на 30% больше суммы, взятой в кредит. Найдите r.

Решение.

Обозначим через сумму кредита, взятого в банке на 19 месяцев. Каждый месяц долг возрастает на %, следовательно, долг на второй месяц составит

,

После увеличения долга, следует выплата в размере рублей. Получаем размер долга на конец второго месяца:

и после упрощения получаем выражение

.

В следующий месяц сумма долга будет равна

с размером выплаты в

после чего сумма долга составит

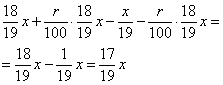
Таким образом, сумма выплат через 19 месяцев составит

или в виде

По условию задачи сумма выплат на 30% больше суммы взятой в кредит, т.е. составляет , то есть получаем равенство

.

Отсюда находим :

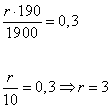
Ответ: 3% в месяц.

Вариант 8

Задание 17. 15 января планируется взять кредит в банке на сумму 1,8 млн рублей на 24 месяца. Условия его возврата таковы:

- 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;

- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

- 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.

Какую сумму нужно вернуть банку в течение первого года кредитования?

Решение.

Взят кредит на сумму 1,8 млн рублей. В следующий месяц кредит возрастает на 2%, что составит рублей. Чтобы долг уменьшался на равную величину каждый месяц в первый месяц нужно заплатить рублей. Таким образом, на конец второго месяца долг будет равен

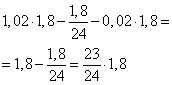
Аналогично для следующего месяца. Долг увеличивается на 2%:

и выплачивается сумма в размере :

.

Таким образом, через 12 месяцев (1 год) будем иметь суммы выплат равные

или в виде

Таким образом, в первый год нужно будет выплатить 1,233 млн. руб.

Ответ: 1233000.

Вариант 11

Задание 17. В июле планируется взять кредит в банке на сумму 4,5 млн рублей на срок 9 лет. Условия его возврата таковы:

- каждый январь долг возрастает на r% по сравнению с концом предыдущего года;

- с февраля по июнь каждого года необходимо выплатить часть долга;

- в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.

Найдите r, если известно, что наибольший годовой платёж по кредиту составит не более 1,4 млн рублей, а наименьший - не менее 0,6 млн рублей.

Решение.

Обозначим через размер кредита, т.е. млн рублей. По условию задачи каждый год кредит увеличивается на r%, т.е. становится равный , а затем, делается платеж так, чтобы сумма долга уменьшалась на одну и ту же величину, т.е. в первый раз платеж должен быть равен и долг становится

.

На следующий год осуществляются подобные действия, долг увеличивается на r%, а платеж вносится в размере :

.

В последний год сумма платежа будет равна

.

Из этих выражений видно, что максимальная сумма платежа приходится на 1-й год, а минимальная - на последний. Следовательно, получаем два неравенства:

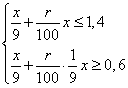
Выражаем неизвестное r, подставляем вместо , получим

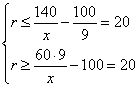
Следовательно, % годовых.

Ответ: 20.

Вариант 12

Задание 17. 31 декабря 2014 года Алексей взял в банке 9282000 рублей в кредит по 10% годовых. Схема выплаты следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Алексей переводит в банк Х рублей. Какой должна быть сумма Х, чтобы Алексей выплатил долг четырьмя равными платежами (то есть за четыре года)?

Решение:

Пусть сумма кредита равна А₀=9282000 рублей, а годовые обозначим через р%. Тогда 31 декабря каждого года оставшаяся сумма долга будет: А_n=А_n-1 + *А_n-1 =А₀*(1 + )ⁿ

Рассмотрим подробней:

Пусть n=1, т.е. рассмотрим первый год. Тогда сумма долга составит А₁=А₀ + *А₀ =А₀*(1 + ).

Для упрощения повторяющуюся часть формулы (1 + ) обозначим через b=(1 + )=(1+0,01*p).

Тогда А₁=А₀*(1 + )=А₀*b.После первой выплаты сумму долга cоставит:

А₁¹= А₀*b-Х.

После второй выплаты сумма долга составит:

А₂¹=А₁¹*b-X= (А₀*b-Х)*b-X= А₀*b²-X*b-X= А₀*b²-(1+b)*X

После третьей выплаты сумма долга составит:

А₃¹=А₂¹*b-X= (А₀*b²-(1+b)*Х)*b-X= А₀*b³-X*b²-X*b-X= А₀*b³-(1+b+b²)*X= А₀*b³-*X= А₀*b³- *X.

Аналогично рассуждая, получим что:

А₄¹= А₀*b⁴- *X

По условию Алексей должен погасить долг за 4 года, поэтому А₀*b⁴- *X=0. Следовательно, X=

Очевидно, что b=(1+0,1)=1,1

X=(928000*1,4641*0,1)/0,4641=2928200

Ответ: 2928200

Вариант 13

Задание 17. 15 января планируется взять кредит в банке на 21 месяц. Условия его возврата таковы:

- 1-го числа каждого месяца долг возрастает на 1 % по сравнению с концом предыдущего месяца;

- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

- 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.

Известно, что на 11-й месяц кредитования нужно выплатить 44,4 тыс. рублей. Какую сумму нужно вернуть банку в течение всего срока кредитования?

Решение.

Пусть тыс. рублей сумма взятого кредита в банке. В первый месяц сумма долга увеличивается на 1%, что составит тыс. рублей. Долг выплачивается в течение 21 месяца так, чтобы долг на одну и ту же величину был меньше долга на 15-е число предыдущего месяца. То есть, после первого месяца нужно выплатить тыс. рублей. Оставшаяся сумма долга будет равна

тыс. рублей.

После второго месяца сумма долга будет равна , а выплата составит . Сумма долга будет равна

.

Таким образом, на 11-й месяц нужно выплатить

или в виде

По условию задачи выплата на 11-й месяц кредитования составила 44,4 тыс. рублей. Получаем уравнение

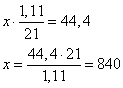
Имеем кредит, равный 840 тыс. рублей. Тогда общая сумма выплат в течение 21 месяца составит

или в виде

То есть 932,4 тыс. рублей или 932400 рублей.

Ответ: 932400.

Вариант 14

Задание 17. 15 января планируется взять кредит в банке на 24 месяца. Условия его возврата таковы:

- 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;

- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

- 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.

Известно, что в течение первого года кредитования нужно вернуть банку 466,5 тыс. рублей. Какую сумму планируется взять в кредит?

Решение.

Пусть тыс. рублей требуется взять в кредит. В начале второго месяца сумма кредита увеличивается на 3%, т.е. становится равной . После этого идет погашение части кредита так, чтобы долг уменьшался на одну и ту же величину, т.е. во втором месяце погашается тыс. рублей. Таким образом, сумма долга в конце второго месяца составляет

.

По аналогии в третьем месяце сумма кредита увеличивается на 3%, т.е. равна и уменьшается на величину . Сумма долга становится равной

.

Таким образом, через 12 месяцев (1 год) выплаченная сумма долга составит

или в виде

которая по условию задачи равна 466,5 тыс. рублей. Получаем уравнение

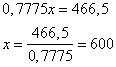
То есть кредит составлял 600 тыс. рублей.

Ответ: 600 000.

Вариант 17

Задание 17. 31 декабря 2014 года Арсений взял в банке 1 млн рублей в кредит. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на определённое количество процентов), затем Арсений переводит очередной транш. Арсений выплатил кредит за два транша, переведя в первый раз 550 тыс. рублей, во второй 638,4 тыс. рублей. Под какой процент банк выдал кредит Арсению?

Решение.

Пусть процентная ставка, под которую был выдан кредит Арсению. Сначала долг 1000 тыс. рублей увеличивается на процентную ставку, т.е. становится равным

,

а, затем, погашается в размере 550 тыс. рублей:

.

Данная сумма долга вновь увеличивается на процентную ставку и погашается в размере 638,4 тыс. рублей:

.

Раскрываем скобки, упрощаем:

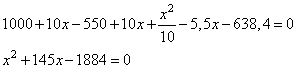
Решаем квадратное уравнение, получаем

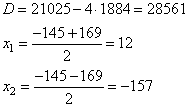
Так как процентная ставка не может быть отрицательным значением, имеем ответ , т.е. 12% годовых.

Ответ: 12.

Транш - доля займа, кредита какой-л. платёжной суммы, передаваемая в виде одной порции.