- Учителю
- Рабочая программа по алгебре для 7 класса по учебнику Макарычева Ю. Н.
Рабочая программа по алгебре для 7 класса по учебнику Макарычева Ю. Н.
Рабочая программа учебного курса Алгебра для 7 класса
Пояснительная записка
Рабочая программа учебного курса Алгебра для 7 класса составлена на основе:
- Федерального компонента государственного образовательного стандарта, утвержденного Приказом Минобразования РФ от 05.03.2004 года № 1089;
- Федерального базисного учебного плана общеобразовательных учреждений РФ, утвержденного приказом Министерства образования РФ № 1312 от 09.03.2004;
- Программы общеобразовательных учреждений, Алгебра 7-9 классы. Составитель: Т.А. Бурмистрова. Москва «Просвещение», 2009 год.
Данная рабочая программа составлена для изучения алгебры по учебнику Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б., под редакцией Теляковского С.А. «Алгебра 7 класс» - М.: Просвещение, 2013.
Содержание программы направлено на освоение учащимися знаний, умений и навыков на базовом уровне. Она включает все темы, предусмотренные федеральным компонентом государственного образовательного стандарта основного общего образования по математике.
Программа рассчитана на 123 часа: 5 ч в неделю в I четверти, 3 ч в неделю во II-IV четвертях. 10 часов отведено для проведения текущих контрольных работ.
Промежуточная аттестация проводится в форме тестов, контрольных и самостоятельных работ. Итоговая аттестация - согласно Уставу образовательного учреждения.
Цель программы обучения:
- овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
- интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;
- формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
- воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.
Задачи программы обучения:
-развитие и углубление вычислительных навыков и умений до уровня, позволяющего уверенно применять знания при решении задач математики, физики и химии:
-ввести понятие функции и научить правильно применять знания о функции в старших классах;
-систематизировать и обобщить сведения о преобразовании выражений, решении линейных уравнений;
-изучить формулы умножения и научить уверенно, применять эти формулы при преобразовании выражений и решении уравнений;
-научить решать системы уравнений и текстовые задачи с помощью систем;
-ввести понятие степени с натуральным показателем и научить упрощать выражения со степенями, находить значения выражений со степенями.
-изучить начальный курс статистики и теории вероятностей.
Формы организации учебного процесса:
индивидуальные, групповые, индивидуально-групповые, фронтальные, классные и внеклассные.
Формы контроля:
Самостоятельная работа, контрольная работа, наблюдение, зачёт, работа по карточке.
Технические средства обучения:
компьютер, медиапроектор.
Учебно-тематический план
-
№ п/п
Название раздела
Количество
часов
Формы контроля
Выражения. Тождества. Уравнения.
25
Контрольные работы - 2
Текущий контроль
Функции.
15
Контрольные работы - 1
Текущий контроль
Степень с натуральным показателем.
19
Контрольные работы - 1
Текущий контроль
Многочлены.
21
Контрольные работы - 2
Текущий контроль
Формулы сокращенного умножения.
21
Контрольные работы - 2
Текущий контроль
Системы линейных выражений.
16
Контрольные работы - 1
Текущий контроль
Повторение
6
Контрольные работы - 1
Итого
123
10
СОДЕРЖАНИЕ КУРСА
1. Выражения, тождества, уравнения (25часов)
Числовые выражения с переменными. Простейшие преобразования выражений. Уравнение, корень уравнения. Линейное уравнение с одной переменной. Решение текстовых задач методом составления уравнений. Статистические характеристики.
Цель: систематизировать и обобщить сведения о преобразованиях алгебраических выражений и решении уравнений с одной переменной.
Первая тема курса 7 класса является связующим звеном между курсом математики 5-6 классов и курсом алгебры. В ней закрепляются вычислительные навыки, систематизируются и обобщаются сведения о преобразованиях выражений и решении уравнений.
Нахождение значений числовых и буквенных выражений даёт возможность повторить с обучающимися правила действий с рациональными числами. Умения выполнять арифметические действия с рациональными числами являются опорными для всего курса алгебры. Следует выяснить, насколько прочно овладели ими учащиеся, и в случае необходимости организовать повторение с целью ликвидации выявленных пробелов. Развитию навыков вычислений должно уделяться серьезное внимание и в дальнейшем при изучении других тем курса алгебры.
В связи с рассмотрением вопроса о сравнении значений выражений расширяются сведения о неравенствах: вводятся знаки ≥ и ≤, дается понятие о двойных неравенствах.
При рассмотрении преобразований выражений формально-оперативные умения остаются на том же уровне, учащиеся поднимаются на новую ступень в овладении теорией. Вводятся понятия «тождественно равные выражения», «тождество», «тождественное преобразование выражений», содержание которых будет постоянно раскрываться и углубляться при изучении преобразований различных алгебраических выражений. Подчеркивается, что основу тождественных преобразований составляют свойства действий над числами.
Усиливается роль теоретических сведений при рассмотрении уравнений. С целью обеспечения осознанного восприятия обучающимися алгоритмов решения уравнений вводится вспомогательное понятие равносильности уравнений, формулируются и разъясняются на конкретных примерах свойства равносильности. Дается понятие линейного уравнения и исследуется вопрос о числе его корней. В системе упражнений особое внимание уделяется решению уравнений вида ах=b при различных значениях а и b. Продолжается работа по формированию у обучающихся умения использовать аппарат уравнений как средство для решения текстовых задач. Уровень сложности задач здесь остается таким же, как в 6 классе.
Изучение темы завершается ознакомлением обучающихся с простейшими статистическими характеристиками: средним арифметическим, модой, медианой, размахом. Учащиеся должны уметь пользовать эти характеристики для анализа ряда данных в несложных ситуациях.
2. Функции (15часов)
Функция, область определения функции. Вычисление значений функции по формуле. График функции. Прямая пропорциональность и ее график. Линейная функция и её график.
Цель: ознакомить обучающихся с важнейшими функциональными понятиями и с графиками прямой пропорциональности и линейной функции общего вида.
Данная тема является начальным этапом в систематической функциональной подготовке обучающихся. Здесь вводятся такие понятия, как функция, аргумент, область определения функции, график функции. Функция трактуется как зависимость одной переменной от другой. Учащиеся получают первое представление о способах задания функции. В данной теме начинается работа по формированию у обучающихся умений находить по формуле значение функции по известному значению аргумента, выполнять ту же задачу по графику и решать по графику обратную задачу.
Функциональные понятия получают свою конкретизацию при изучении линейной функции и ее частного вида - прямой пропорциональности. Умения строить и читать графики этих функций широко используются как в самом курсе алгебры, так и в курсах геометрии и физики. Учащиеся должны понимать, как влияет знак коэффициента на расположение в координатной плоскости графика функции у=кх, где к
0, как зависит от значений к и b взаимное расположение графиков двух функций вида у=кх+b.
Формирование всех функциональных понятий и выработка соответствующих навыков, а также изучение конкретных функций сопровождаются рассмотрением примеров реальных зависимостей между величинами, что способствует усилению прикладной направленности курса алгебры.
3. Степень с натуральным показателем (19 часов)
Степень с натуральным показателем и ее свойства. Одночлен. Функции у=х2, у=х3 и их графики.
Цель: выработать умение выполнять действия над степенями с натуральными показателями.
В данной теме дается определение степени с натуральным показателем. В курсе математики 6 класса учащиеся уже встречались с примерами возведения чисел в степень. В связи с вычислением значений степени в 7 классе дается представление о нахождении значений степени с помощью калькулятора; Рассматриваются свойства степени с натуральным показателем: На примере доказательства свойств аm · аn = аm+n; аm : аn = аm-n, где m > n; (аm)n = аm·n; (ab)m = ambm учащиеся впервые знакомятся с доказательствами, проводимыми на алгебраическом материале. Указанные свойства степени с натуральным показателем находят применение при умножении одночленов и возведении одночленов в степень. При нахождении значений выражений содержащих степени, особое внимание следует обратить на порядок действий.
Рассмотрение функций у=х2, у=х3 позволяет продолжить работу по формированию умений строить и читать графики функций. Важно обратить внимание обучающихся на особенности графика функции у=х2:график проходит через начало координат, ось Оу является его осью симметрии, график расположен в верхней полуплоскости.
Умение строить графики функций у=х2 и у=х3 используется для ознакомления обучающихся с графическим способом решения уравнений.
4. Многочлены (21 часов)
Многочлен. Сложение, вычитание и умножение многочленов. Разложение многочленов на множители.
Цель: выработать умение выполнять сложение, вычитание, умножение многочленов и разложение многочленов на множители.
Данная тема играет фундаментальную роль в формировании умения выполнять тождественные преобразования алгебраических выражений. Формируемые здесь формально-оперативные умения являются опорными при изучении действий с рациональными дробями, корнями, степенями с рациональными показателями.
Изучение темы начинается с введения понятий многочлена, стандартного вида многочлена, степени многочлена. Основное место в этой теме занимают алгоритмы действий с многочленами - сложение, вычитание и умножение. Учащиеся должны понимать, что сумму, разность, произведение многочленов всегда можно представить в виде многочлена. Действия сложения, вычитания и умножения многочленов выступают как составной компонент в заданиях на преобразования целых выражений. Поэтому нецелесообразно переходить к комбинированным заданиям прежде, чем усвоены основные алгоритмы.
Серьезное внимание в этой теме уделяется разложению многочленов на множители с помощью вынесения за скобки общего множителя и с помощью группировки. Соответствующие преобразования находят широкое применение как в курсе 7 класса, так и в последующих курсах, особенно в действиях с рациональными дробями.
В данной теме учащиеся встречаются с примерами использования рассматриваемых преобразований при решении разнообразных задач, в частности при решении уравнений. Это позволяет в ходе изучения темы продолжить работу по формированию умения решать уравнения, а также решать задачи методом составления уравнений. В число упражнений включаются несложные задания на доказательство тождества.
5. Формулы сокращенного умножения (21 час)
Формулы (а - b )(а + b ) = а2 - b 2, (а ± b)2 = а2± 2а b + b2, (а ± b)3 = а3 ± За2b + За b2 ± b3, (а ± b) (а2 
а b + b2) = а3 ± b3. Применение формул сокращённого умножения в преобразованиях выражений.
Цель: выработать умение применять формулы сокращенного умножения в преобразованиях целых выражений в многочлены и в разложении многочленов на множители.
В данной теме продолжается работа по формированию у обучающихся умения выполнять тождественные преобразования целых выражений. Основное внимание в теме уделяется формулам (а - b)(а + b) = а2 - b 2, (а ± b)2 = а2± 2а b + b2. Учащиеся должны знать эти формулы и соответствующие словесные формулировки, уметь применять их как «слева направо», так и «справа налево».
Наряду с указанными рассматриваются также формулы (а ± b)3 = а3 ± За2b + За b2 ± b3, (а ± b) (а2 а b + b2) = а3 ± b3. Однако они находят меньшее применение в курсе, поэтому не следует излишне увлекаться выполнением упражнений на их использование.
В заключительной части темы рассматривается применение различных приемов разложения многочленов на множители, а также использование преобразований целых выражений для решения широкого круга задач.
6. Системы линейных уравнений (16 часов)
Система уравнений. Решение системы двух линейных уравнений с двумя переменными и его геометрическая интерпретация. Решение текстовых задач методом составления систем уравнений.
Цель: ознакомить обучающихся со способом решения систем линейных уравнений с двумя переменными, выработать умение решать системы уравнений и применять их при решении текстовых задач.
Изучение систем уравнений распределяется между курсами 7 и 9 классов. В 7 классе вводится понятие системы и рассматриваются системы линейных уравнений.
Изложение начинается с введения понятия «линейное уравнение с двумя переменными». В систему упражнений включаются несложные задания на решение линейных уравнений с двумя переменными в целых числах.
Формируется умение строить график уравнения ах + bу=с, где а≠0 или b≠0, при различных значениях а, b, с. Введение графических образов даёт возможность наглядно исследовать вопрос о числе решений системы двух линейных уравнений с двумя переменными.
Основное место в данной теме занимает изучение алгоритмов решения систем двух линейных уравнений с двумя переменными способом подстановки и способом сложения. Введение систем позволяет значительно расширить круг текстовых задач, решаемых с помощью аппарата алгебры. Применение систем упрощает процесс перевода данных задачи с обычного языка на язык уравнений.
7. Повторение (6 часов)
Цель: повторение, обобщение и систематизация знаний, умений и навыков за курс алгебры 7 класса.
Итоговая контрольная работа.
Календарно - тематическое планирование уроков алгебры в 7 классе.
№ урока
Дата
Содержание учебного материала
Кол-во часов
Тип урока
по плану
фактически
1 четверть ( 43 урока)
Глава 1. Выражения, тождества, уравнения
25
§ 1. Выражения.
5
1
Числовые выражения.
1
Изучение нов материала.
2
Нахождение значений числовых выражений.
1
Закрепление знаний, выработка умений и нав
3
Выражение с переменной и его числовое значение
1
Изучение ново материала.
4
Решение задач по теме «Выражения с переменными»
1
Закрепление знаний, выработка умений и нав
5
Сравнение значений выражений.
1
Изучение нов материала.
§ 2. Преобразование выражений.
6
6
Основные свойства сложения и умножения чисел
1
Изучение нов материала, закрепление знаний.
7
Решение задач по теме «Свойства действий над числами»
1
Закрепление знаний, выработка умений и нав
8
Понятие тождества. Доказательство тождеств
1
Изучение нов материала, закрепление знаний
9
Тождественные преобразование выражений.
1
Закрепление знаний, выработка умений и нав
10
Выражения. Тождества
1
Обобщение и систематиз изученного
11
Контрольная работа № 1. Преобразование выражений.
1
Проверка умений и навыков
§ 3. Уравнения с одной переменной.
8
12
Уравнение и его корни.
1
Изучение нов материала.
13
Понятие линейного уравнения с одной переменной.
1
Закрепление знаний, выработка умений и нав
14
Решение уравнений, сводящихся к линейным
1
Закрепление знаний, выработка умений и нав
15
Решение задач по теме «Линейное уравнение с одной переменной»
1
Закрепление знаний, выработка умений и нав
16
Составление уравнения по условию задачи
1
Изучение нов материала.
17
Решение задач с помощью уравнений, сводящихся к линейным
1
Закрепление знаний, выработка умений и нав
18
Уравнения с одной переменной
1
Обобщение и систематиз изученного
Статистические характеристики.
6
19
Среднее арифметическое, размах и мода.
1
Изучение нов материала.
20
Использование средних статистических характеристик при решении различных задач
Закрепление знаний, выработка умений и нав
21
Медиана упорядоченного ряда
1
Изучение нов материала, закрепление знаний.
22
Использование средних статистических характеристик при решении задач.
1
Закрепление знаний, выработка умений и нав
23
Решение задач по теме «Уравнения с одной переменной»
1
Обобщение и систематиз знаний.
24
Контрольная работа № 2. Уравнения с одной переменной.
1
Проверка умений и нав
25
Формулы
1
Изучение нов материала, закрепление знаний.
Глава 2. Функции.
15
§ 4. Функции и их графики.
5
26
Понятие функции. Область определения.
1
Изучение нов материала.
27
Аналитический способ задания функции
1
Закрепление знаний, выработка умений и нав
28
Вычисление значений функции, заданной формулой
1
Изучение нов материала, закрепление знаний.
29
График функции.
1
Изучение нов материала.
30
График функции. Решение задач.
1
Закрепление знаний, выработка умений и нав
§ 5. Линейная функция.
10
31
Понятие прямой пропорциональности
1
Изучение нов материала, закрепление знаний
32
График прямой пропорциональности
1
Изучение нов материала, закрепление знаний.
33
Прямая пропорциональность.
1
Закрепление знаний, выработка умений и нав
34
Понятие линейной функции и ее график
1
Изучение нов материала.
35
Взаимное расположение графиков линейных функций.
1
Изучение нов материала, закрепление знаний.
36
Решение задач по теме «Линейная функция и ее график»
1
Закрепление знаний, выработка умений и нав
37
Построение графиков функций
1
Закрепление знаний, выработка умений и нав
38
Линейная функция
1
Обобщение и систематиз изученного
39
Контрольная работа № 3. Функции и их графики.
1
Проверка умений и нав
40
Задание функции несколькими формулами
1
Закрепление знаний, выработка умений и нав
Глава 3. Степень с натуральным показателем.
19
§ 6. Степень и его свойства.
10
41
Определение степени с натуральным показателем
1
Изучение нов материала.
42
Нахождения значения степени.
1
Закрепление знаний, выработка умений и нав
43
Умножение и деление степеней с одинаковыми основаниями
1
Изучение нов материала, закрепление знаний.
2 четверть ( 23 урока)
44
Умножение и деление степеней
1
Закрепление знаний, выработка умений и нав
45
Решение задач по теме «Умножение и деление степеней»
1
Закрепление знаний, выработка умений и нав
46
Возведение в степень произведения
1
Изучение нов материала, закрепление знаний
47
Возведение степени в степень
1
Изучение нов материала, закрепление знаний
48
Упрощение выражений, содержащих степень
1
Закрепление знаний, выработка умений и нав
49
Степень с натуральным показателем
1
Закрепление знаний, выработка умений и нав
50
Решение задач по теме «Возведение в степень произведения и степени»
1
Обобщение и систематиз изученного
§ 7. Одночлены.
9
51
Одночлен и его стандартный вид.
1
Изучение нов материала.
52
Умножение одночленов.
1
Изучение нов материала, закрепление знаний.
53
Возведение одночлена в степень.
1
Закрепление знаний, выработка умений и нав
54
Умножение одночленов. Возведение одночлена в степень.
1
Обобщение и систематиз изученного
55
Функция у=х2 и у=х3 и их графики
1
Изучение нов материала, закрепление знаний.
56
Графическое решение уравнений вида у=х2 и у=х3
1
Изучение нов материала, закрепление знаний
57
Степень с натуральным показателем
1
Обобщение и систематиз изученного
58
Контрольная работа № 4. Степень и его свойства. Одночлены.
1
Проверка умений и нав
59
О простых и составных числах
1
Изучение нов материала, закрепление знаний
Глава 4. Многочлены.
21
§ 9. Сумма и разность многочленов.
5
60
Многочлен и его стандартный вид.
1
Изучение нов материала.
61
Нахождение значений многочлена
1
Закрепление знаний, выработка умений и нав
62
Правило сложения и вычитания многочленов
1
Изучение нов материала
63
Решение упражнений на сложение и вычитание многочленов
1
Выработка умений и нав
64
Заключение многочлена в скобки
1
Изучение нов материала
§ 10. Произведение одночлена и многочлена.
7
65
Умножение одночлена на многочлен
1
Изучение нов материала, закрепление знаний.
66
Решение уравнений.
1
Закрепление знаний, выработка умений и нав
3 четверть ( 30 уроков)
67
Решение задач с помощью уравнений
1
Закрепление знаний, выработка умений и нав
68
Разложение многочлена на множители способом вынесения общего множителя за скобки.
1
Закрепление знаний, выработка умений и нав
69
Вынесение общего множителя за скобки при решении различных задач
1
Закрепление знаний, выработка умений и нав
70
Подготовка к контрольной работе.
1
Обобщение и систематиз изученного
71
Контрольная работа № 5. Сумма и разность многочленов.
1
Проверка умений и нав
§ 11. Произведение многочленов.
9
72
Умножение многочлена на многочлен.
1
Изучение нов материала, закрепление знаний.
73
Применение правила умножения многочлена на многочлен
1
Закрепление знаний, выработка умений и нав
74
Доказательство тождеств и утверждений
1
Закрепление знаний, выработка умений и нав
75
Решение уравнений и задач на составление уравнений
1
Изучение нов материала, закрепление знаний.
76
Способ группировки разложения многочлена на множители
1
Изучение нов материала, закрепление знаний
77
Применение способа группировки разложения многочлена на множители.
1
Закрепление знаний, выработка умений и нав
78
Доказательство тождеств.
1
Изучение нов материала, закрепление знаний
79
Контрольная работа № 6. Произведение многочленов.
1
Проверка умений и нав
80
Деление с остатком
1
Изучение нов материала, закрепление знаний
Глава 5. Формулы сокращенного умножения.
21
§ 12. Квадрат суммы и квадрат разности.
5
81
Формулы квадрата суммы и разности двух выражений.
1
Изучение нов материала, закрепление знаний.
82
Преобразование выражений с использованием формул квадрата суммы и разности.
1
Закрепление знаний, выработка умений и нав
83
Применение формул квадрата суммы и квадрата разности.
1
Закрепление знаний, выработка умений и нав
84
Изучение способа разложения на множители с помощью формул квадрата суммы и разности
1
Изучение нов материала, закрепление знаний.
85
Применение способа разложения на множители с помощью квадрата суммы и разности
1
Проверка умений и нав
§ 13. Разность квадратов. Сумма и разность кубов.
8
86
Умножение разности двух выражений на их сумму.
1
Изучение нов материала, закрепление знаний.
87
Применение формулы умножения разности двух выражений на их сумму
1
Закрепление знаний, выработка умений и нав
88
Применение формул сокращенного умножения к преобразованию выражений
1
Закрепление знаний, выработка умений и нав
89
Изучение формулы разности квадратов
1
Изучение нов материала, закрепление знаний.
90
Применение формулы разности квадратов для разложения многочлена на множители
1
Закрепление знаний, выработка умений и нав
91
Применение формулы разности квадратов при решении задач
1
Закрепление знаний, выработка умений и нав
92
Контрольная работа № 7. Формулы сокращенного умножения.
1
Проверка умений и нав
93
Разложение на множители суммы и разности кубов
1
Изучение нов материала, закрепление знаний.
§ 14. Преобразование целых выражений.
8
94
Понятие целого выражения
1
Изучение нов материала, закрепление знаний.
95
Преобразование целых выражений.
1
Закрепление знаний, выработка умений и нав
96
Три способа разложения многочлена на множители
1
Закрепление знаний, выработка умений и нав
4 четверть (27уроков)
97
Разложение многочлена на множители разными способами
1
Проверка умений и нав
98
Разложение многочлена на множители при решении задач
1
Закрепление знаний, выработка умений и нав
99
Применение преобразований целых выражений.
1
Обобщение и систематизац изученного
100
Контрольная работа № 8. Преобразование целых выражений.
1
Проверка умений и нав
101
Возведение двучлена в степень
1
Изучение нов материала, закрепление знаний.
Глава 6. Системы линейных уравнений.
16
§ 15. Линейные уравнения с двумя переменными и их системы.
6
102
Линейное уравнение с двумя переменными.
1
Изучение нов материала.
103
Решение линейных уравнений с двумя переменными.
1
Изучение нов материала, закрепление знаний.
104
Понятие графика линейного уравнения с двумя переменными
1
Изучение нов материала, закрепление знаний.
105
Построение графика линейного уравнения с двумя переменными
1
Закрепление знаний, выработка умений и нав
106
Понятие системы уравнений с двумя переменными
1
Изучение нов материала, закрепление знаний.
107
Графическое решение систем линейных уравнение с двумя переменными
1
Изучение нов материала, закрепление знаний.
§ 16. Решение систем линейных уравнений.
10
108
Способ подстановки.
1
Изучение нов материала, закрепление знаний.
109
Решение систем линейных уравнений способом подстановки.
1
Закрепление знаний, выработка умений и нав
110
Решение примеров. Способ подстановки.
1
Проверка умений и нав
111
Способ сложения.
1
Изучение нов материала, закрепление знаний.
112
Решение систем линейных уравнений способом сложения.
1
Закрепление знаний, выработка умений и нав
113
Составление уравнений прямой, проходящей через две заданные точки
1
Закрепление знаний, выработка умений и нав
114
Составление системы уравнений по условию задачи
1
Изучение нов материала, закрепление знаний.
115
Решение задачи «на движение» с помощью систем уравнений
1
Закрепление знаний, выработка умений и нав
116
Решение задач
1
Обобщение и систематизац изученного
117
Контрольная работа № 9. Системы двух линейных уравнений с двумя переменными.
1
Проверка умений и нав
Повторение
6
118
Степень с натуральным показателем. Одночлен
1
Обобщение и систематизац изученного
119
Многочлены и действия с ними
1
Обобщение и систематизац изученного
120
Формулы сокращенного умножения
1
Обобщение и систематизац изученного
121
Линейная функция и ее график
1
Обобщение и систематизац изученного
122
Системы линейных уравнений с двумя переменными
1
Обобщение и систематизац изученного
123
Итоговая контрольная работа
1
Проверка умений и навыков
Требования к уровню подготовки учащихся
В результате изучения курса алгебры 7 класса обучающиеся должны:
знать/понимать
-
существо понятия математического доказательства; примеры доказательств;
-
существо понятия алгоритма; примеры алгоритмов;
-
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
-
как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
-
как потребности практики привели математическую науку к необходимости расширения понятия числа;
-
примеры статистических закономерностей и выводов;
-
каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики.
Алгебра
уметь
-
составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;
-
выполнять основные действия со степенями с натуральными показателями, с многочленами; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
-
решать линейные уравнения решать линейные решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;
-
изображать числа точками на координатной прямой;
-
определять координаты точки плоскости, строить точки с заданными координатами;
-
находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
-
применять графические представления при решении уравнений, систем, неравенств;
-
описывать свойства изученных функций (у=кх, где к
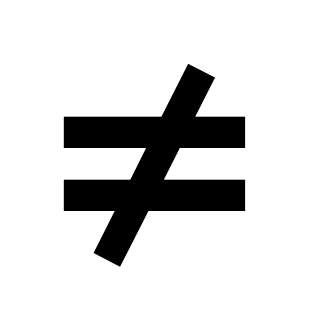0, у=кх+b, у=х2, у=х3), строить их графики.
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных материалах;
-
моделирования практических ситуаций и исследовании построенных моделей с использованием аппарата алгебры;
-
описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;
-
интерпретации графиков реальных зависимостей между величинами.
Элементы логики, комбинаторики, статистики и теории вероятностей
уметь
-
проводить несложные доказательства, получать простейшие следствия из известных или ранее полученных утверждений, оценивать логическую правильность рассуждений, использовать примеры для иллюстрации и контрпримеры для опровержения утверждений;
-
решать комбинаторные задачи путем систематического перебора возможных вариантов, вычислять средние значения результатов измерений;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
выстраивания аргументации при доказательстве (в форме монолога и диалога);
-
распознавания логически некорректных рассуждений;
-
записи математических утверждений, доказательств;
-
анализа реальных числовых данных, представленных в виде диаграмм, графиков, таблиц;
-
решения практических задач в повседневной и профессиональной деятельности с использованием действий с числами, процентов, длин, площадей, объемов, времени, скорости;
-
решения учебных и практических задач, требующих систематического перебора вариантов;
-
понимания статистических утверждений.
Программно-методическое обеспечение
Для реализации рабочей программы используется
учебно-методический комплект учителя:
1. Алгебра: учеб. для 7 кл/ Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С. Б. Суворова; под ред. С.А. Теляковского. - М.: Просвещение, 2013.
2. Программы общеобразовательных учреждений, Алгебра 7-9 классы. Составитель: Т.А. Бурмистрова. - М.: Просвещение, 2009.
3. Макарычев Ю.Н. Алгебра: элементы статистики и теории вероятностей: учеб. пособие для 7-9 кл. / Ю.Н. Макарычев, Н.Г. Миндюк. - М.: Просвещение, 2009.
4. Звавич Л.И. Алгебра: дидактические материалы для 7 кл./ Л.И. Звавич, Л.В. Кузнецова, С.Б. Суворова.- М.: Просвещение, 2012.
5. Дидактические материалы по алгебре 7 класс к учебнику Ю.Н. Макарычева «Алгебра 7 класс»/ Л.И. Звавич, Н.В. Дьяконова. - М.: Экзамен, 2013
6. Контрольные работы по алгебре 7 класс/ Ю.П. Дудницын, В.Л. Кронгауз.-М.:
Экзамен, 2013
7. Макарычев Ю.Н. Изучение алгебры в 7-9 классах/ Ю.Н. Макарычев, Н.Г. Миндюк, С.Б. Суворова. - М.: Просвещение, 2011.
учебно-методический комплект ученика:
1. Алгебра: учеб. для 7 кл/ Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С. Б. Суворова; под ред. С.А. Теляковского. - М.: Просвещение, 2013.
2. Макарычев Ю.Н. Алгебра: элементы статистики и теории вероятностей: учеб. пособие для 7-9 кл. / Ю.Н. Макарычев, Н.Г. Миндюк. - М.: Просвещение, 2009.
3. Звавич Л.И. Алгебра: дидактические материалы для 7 кл./ Л.И. Звавич, Л.В. Кузнецова, С.Б. Суворова.- М.: Просвещение, 2012.
Критерии и нормы оценки знаний, умений и навыков обучающихся
1. Оценка письменных контрольных работ обучающихся
Ответ оценивается отметкой «5», если:
- работа выполнена полностью;
- в логических рассуждениях и обосновании решения нет пробелов и ошибок;
- в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
- работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
- допущены одна ошибка или есть два - три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
- допущено более одной ошибки или более двух - трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
- допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.
Отметка «1» ставится в следующих случаях:
- работа показала полное отсутствие у обучающегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.
Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других задании.
2. Оценка устных ответов обучающихся
Ответ оценивается отметкой «5», если ученик:
- полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
- изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
- правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
- показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
- продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
- отвечал самостоятельно, без наводящих вопросов учителя;
- возможны одна - две неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
- в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
- допущены один - два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
- допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
- неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала;
- имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
- ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
- при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
- не раскрыто основное содержание учебного материала;
- обнаружено незнание учеником большей или наиболее важной части учебного материала;
- допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Отметка «1» ставится в следующих случаях:
- ученик обнаружил полное незнание и непонимание изучаемого учебного материала или не смог ответить ни на один из поставленных вопросов по изученному материалу.
3. Общая классификация ошибок.
При оценке знаний, умений и навыков учащихся следует учитывать все ошибки (грубые и негрубые) и недочёты.
Грубыми считаются ошибки:
- незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;
- незнание наименований единиц измерения;
- неумение выделить в ответе главное;
- неумение применять знания, алгоритмы для решения задач;
- неумение делать выводы и обобщения;
- неумение читать и строить графики;
- неумение пользоваться первоисточниками, учебником и справочниками;
- потеря корня или сохранение постороннего корня;
- отбрасывание без объяснений одного из них;
- равнозначные им ошибки;
- вычислительные ошибки, если они не являются опиской;
- логические ошибки.
К негрубым ошибкам следует отнести:
- неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;
- неточность графика;
- нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);
- нерациональные методы работы со справочной и другой литературой;
- неумение решать задачи, выполнять задания в общем виде.
Недочетами являются:
- нерациональные приемы вычислений и преобразований;
- небрежное выполнение записей, чертежей, схем, графиков.
Список литературы
1. Алгебра: учеб. для 7 кл/ Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С. Б. Суворова; под ред. С.А. Теляковского. - М.: Просвещение, 2013.
2. Программы общеобразовательных учреждений, Алгебра 7-9 классы. Составитель: Т.А. Бурмистрова. - М.: Просвещение, 2009.
3. Макарычев Ю.Н. Алгебра: элементы статистики и теории вероятностей: учеб. пособие для 7-9 кл. / Ю.Н. Макарычев, Н.Г. Миндюк. - М.: Просвещение, 2009.
4. Звавич Л.И. Алгебра: дидактические материалы для 7 кл./ Л.И. Звавич, Л.В. Кузнецова, С.Б. Суворова.- М.: Просвещение, 2012.
5. Дидактические материалы по алгебре 7 класс к учебнику Ю.Н. Макарычева «Алгебра 7 класс»/ Л.И. Звавич, Н.В. Дьяконова. - М.: Экзамен, 2013
5. Макарычев Ю.Н. Изучение алгебры в 7-9 классах/ Ю.Н. Макарычев, Н.Г. Миндюк, С.Б. Суворова. - М.: Просвещение, 2011.
6. Алгебра. Тематические тесты. 7 класс/ Ю.П. Дудницын, В.Л. Кронгауз.-М.: Просвещение, 2011.
7. Контрольные работы по алгебре 7 класс/ Ю.П. Дудницын, В.Л. Кронгауз.-М.:
Экзамен, 2013
18