Урок геометрии в 7 классе по теме Медиана, биссектриса, высота треугольника

Урок геометрии в 7 классе

Тема: Медиана, биссектриса, высота треугольника.

Автор: Григорян Жанна Виктори,

учитель математики высшей квалификационной категории

2016г.

Тема: Медиана, биссектриса, высота треугольника.

Тип урока: «Исследовательская работа»

Цели урока:

- дидактическая:

сформировать понятия «медиана треугольника», «биссектриса треугольника», «высота треугольника»;

- психологическая:

обучать умению математически грамотно проводить рассуждения; развивать творческое мышление учащихся;

- воспитательная:

активизировать умственную деятельность учащихся.

Оборудование:

1. Интерактивная доска

2. Компьютеры у учащихся

3. Линейка, транспортир, угольник.

4. Карточки для работы готовыми чертежами.

5. Бланк практической работы.

План урока.

1. Мотивация. Постановка учебной задачи.

2. Решение учебной части.

Задание 1.

Установить понятие «высота треугольника».

Задание 2.

Установить понятие «биссектриса треугольника».

Задание 3.

Установить понятие «медиана треугольника».

Задание 4.

Сформулировать свойства высот, биссектрис, медиан треугольника.

1. Обобщение урока. Домашнее задание.

Содержание урока.

1. Ориентировочно-мотивационный этап. 10 минут.

   1. Выравнивание знаний.

Что такое треугольник?

Из каких элементов он состоит?

Первый признак равенства треугольников?

Что такое отрезок?

Что такое середина отрезка?

Что такое биссектриса угла?

2. Постановка цели урока.

Кроме названных вами элементов треугольника в этой фигуре есть еще линии, которые очень важны для дальнейшего изучения геометрии. Важны до такой степени, что их даже называют Замечательные линии треугольника. Какая у нас сегодня цель на уроке? (Формулировка учащимися цели урока)

3. Задание на формулировку темы урока

Распределить треугольники на три группы.

Почему так распределили. В первой группе в треугольнике проведен отрезок, который называется медианой треугольника, во второй группе - биссектриса треугольника. И в третьей группы - высота треугольника.

Историческая справка.

Эти слова пришли к нам из латинского языка. Например, слово «биссектриса» означает «бис» - дважды и «сектио» - рассечение, т.е.«рассекающая надвое». Слово «перпендикуляр» означает «пендула» - маятник, отвес. Таким образом, перпендикуляром называли когда-то просто вертикальное направление. Оно образует прямой угол с земной поверхностью.

Сегодня мы сформулируем определения: «высота треугольника», «медиана треугольника», «биссектриса треугольника» и совместно составим алгоритмы их построения.

2. Операционально-исполнительский этап.

Попробуйте дать определение медианы, глядя на рисунок. Давайте дадим определение медианы треугольника, биссектрисы треугольника, высоты треугольника.

Запоминалки:

Биссектриса - это крыса, которая бегает по углам и делит угол пополам.

Медиана - обезьяна, она идет по сторонам и делит стороны пополам.

Выстота похожа на кота, который выгнет спину и под прямым углом соединит вершину со стороной хвостом.

Задание 1.

Построить отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Сформулировать определение медианы треугольника. Составить алгоритм ее построения.

Самооценка.

Алгоритм построения медианы треугольника.

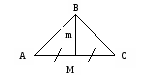
1. Построить ∆АВС.

2. Построить середину стороны АС и обозначить буквой М.

3. Соединить вершину треугольника В с построенной точкой М.

4. Считать отрезок BМ медианой треугольника.

Медиана может быть обозначена буквой m.

Поочередно вывешиваются алгоритмы построения медианы, биссектрисы, высоты треугольника.

Задание 2.

Построить отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны. Сформулировать определение биссектрисы треугольника. Составить алгоритм ее построения.

Самооценка.

Алгоритм построения биссектрисы треугольника.

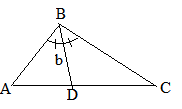
1. Построить ∆АВС.

2. Провести биссектрису угла треугольника при вершине В.

3. Обозначить точку пересечения биссектрисы угла с противолежащей стороной буквой D.

4. Считать отрезок BD биссектрисой треугольника.

Биссектриса может быть обозначена буквой b.

Задание 3.

Провести перпендикуляр из вершины треугольника к прямой, содержащей противоположную сторону. Сформулировать определение высоты треугольника. Составить алгоритм ее построения.

Самооценка.

Алгоритм построения высоты треугольника.

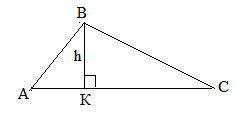
1. Построить ∆АВС.

2. Опустить перпендикуляр из вершины В к прямой, содержащей противоположную сторону АС.

3. Основание перпендикуляра обозначить точкой К.

4. Считать отрезок ВК высотой треугольника.

Высота может быть обозначена буквой h.

Задание 4. Компьютерная лаборатория

Учащиеся выполняют практическую работу в среде «Живая математика» (задание1, задание 2).

На основании полученных результатов делают вывод:

• Медианы любого треугольника пересекаются в одной точке, расположенной внутри треугольника.

• Биссектрисы любого треугольника пересекаются в одной точке, расположенной внутри треугольника.

Учащиеся на листах с готовыми чертежами остроугольного, прямоугольного, тупоугольного треугольников, пользуясь алгоритмом, проводят высоты в каждом треугольнике.

Возникает проблемная ситуация: В тупоугольном треугольнике высоты не пересекаются внутри треугольника. Обращаются к программе «Живая математика». Провот эксперимент.

На основании полученных результатов делают вывод:

• Высоты в остроугольном треугольнике пересеклись в точке, находящейся внутри треугольника.

• Высоты в прямоугольном треугольнике пересеклись в вершине прямого угла.

• Высоты в тупоугольном треугольнике пересеклись в точке, расположенной вне треугольника.

Озвучивание выводов

• Медианы любого треугольника пересекаются в одной точке, расположенной внутри треугольника. Эта точка называется центром тяжести треугольника.

• Биссектрисы любого треугольника пересекаются в одной точке, расположенной внутри треугольника. Эта точка называется центром вписанной окружности.

• Высоты любого треугольника пересекаются в одной точке. Эта точка называется ортоцентром треугольника.

• Высоты в остроугольном треугольнике пересеклись в точке, находящейся внутри треугольника.

• Высоты в прямоугольном треугольнике пересеклись в вершине прямого угла.

• Высоты в тупоугольном треугольнике пересеклись в точке, расположенной вне треугольника.

Историческая справка.

В «Началах» Евклида указывается, что три биссектрисы внутренних углов треугольника пересекаются в одной точке - центре вписанной окружности, но не говорится о том, что высоты пересекаются водной точке (ортоцентре). «Ортос» - греческое слово (прямой, правильный).

Об этом знали Архимед, Прокл. Архимед доказал, что точка пересечения медиан треугольника является центром тяжести (барицентр). На эти точки было обращено внимание, начиная с XVIII века они были названы «замечательными» или «особенными» точками треугольника. Исследование свойств треугольника, связанных с этими точками и другими, послужило началом для создания новой ветви элементарной математики «геометрии треугольника», родоначальником которой был Леонард Эйлер. В 1765 году Эйлер доказал, что в любом треугольнике ортоцентр, барицентр, центр описанной окружности лежат на одной прямой, названной «прямой Эйлера».

Задание 5.

Составить графическую модель усвоенного материала.

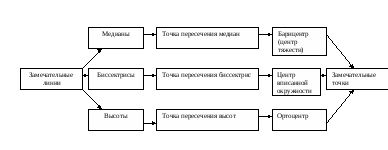
III. Рефлексивно - оценочный этап.

1) Какие цели были поставлены на уроке?

2) Что узнали на уроке?

3) Какие выводы сделали на уроке?

4) Закрыть записи. Проговорить вслух и про себя понятия медианы, биссектрисы, высоты треугольника. Проговорить алгоритмы построения этих элементов треугольника.

5) А сейчас каждый из вас подойдет к доске и покажет свое настроение после урока.

1. Домашнее задание.

1) По учебнику: п. 17, №103, №104;

2) На творческое применение знаний:

• «Головоломка со спичками».

Шесть спичек образуют два равных треугольника. Нужно эти спички расположить так, чтобы они образовали четыре таких же треугольника.

• Подготовить реферат на тему «Замечательные линии и точки треугольника».