- Учителю
- Контрольная работа по комбинаторике
Контрольная работа по комбинаторике
Контрольная работа по комбинаторике.
Вариант 1
-
Вычислите
 .
.
-
Вычислите
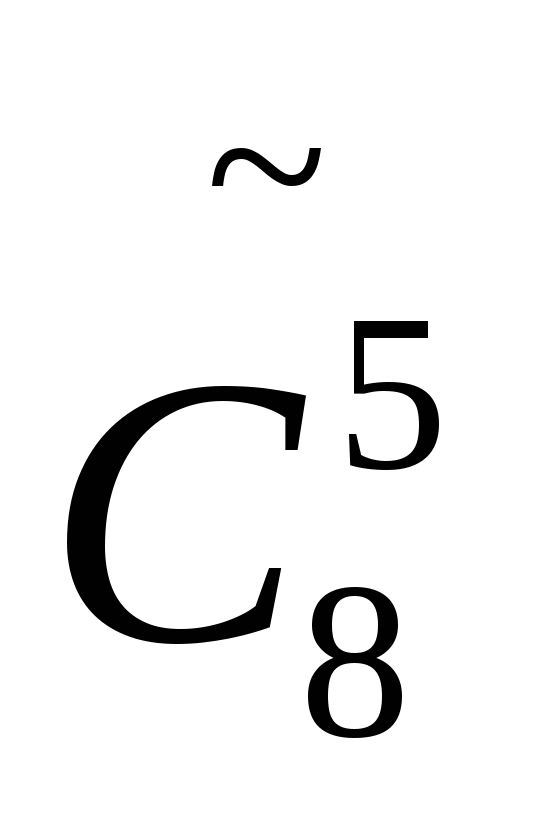 .
.
-
Девять лиц в этот обед сели как попало. Каждый следующий обед они решили пересаживаться на другое место. Сколько раз им придется обедать?
-
В чемпионате по футболу участвуют 16 команд. Сколько имеется вариантов распределения золотых, серебряных и бронзовых медалей?
-
Команда некоторой ЭВМ, записывается в виде набора из восьми цифровых знаков - нулей и единиц. Каково максимальное число различных команд?
-
Сколькими способами тренер баскетбольной команды может из десяти человек, включенных в заявку, составить стартовую пятерку? В баскетболе порядок, в котором тренер называет игроков, выходящих на площадку, роли не играет.
-
Сколькими способами можно 7 одинаковых предметов пронумеровать цифрами 2, 4, 6 и 8.
-
С помощью треугольника Паскаля найдите третий коэффициент в разложении многочлена
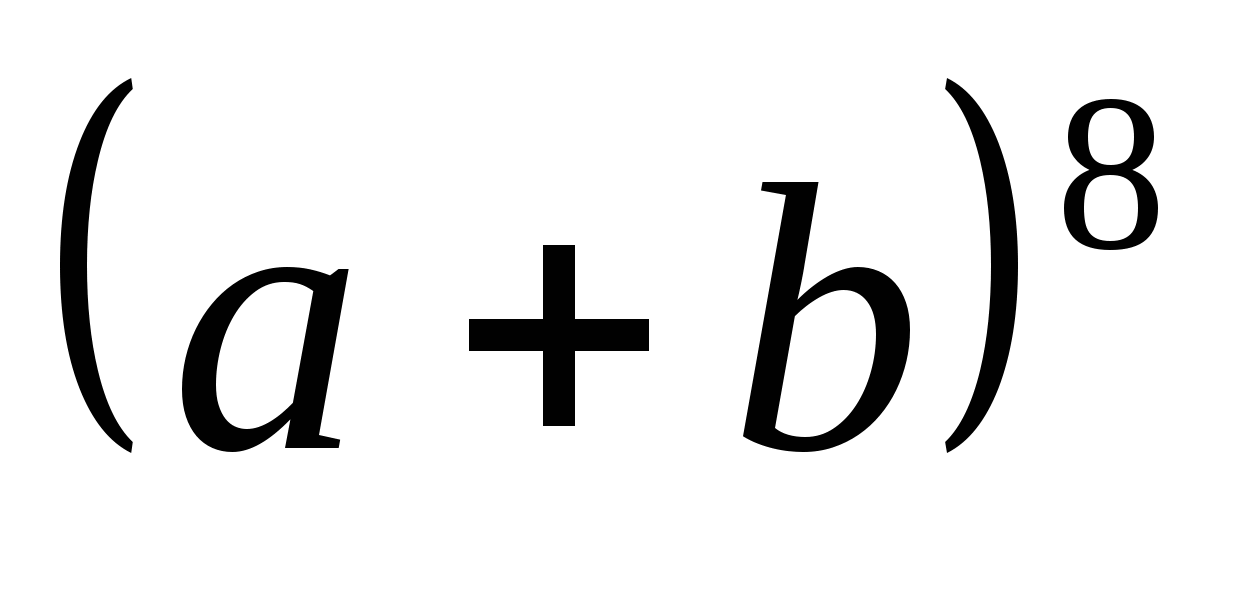 .
.
9. В разложении ![]() седьмой член равен 2,268. Найти значение
седьмой член равен 2,268. Найти значение ![]() , если сумма биномиальных
коэффициентов равна 512.
, если сумма биномиальных
коэффициентов равна 512.
________________________________________________________________
Вариант 2
-
Вычислите
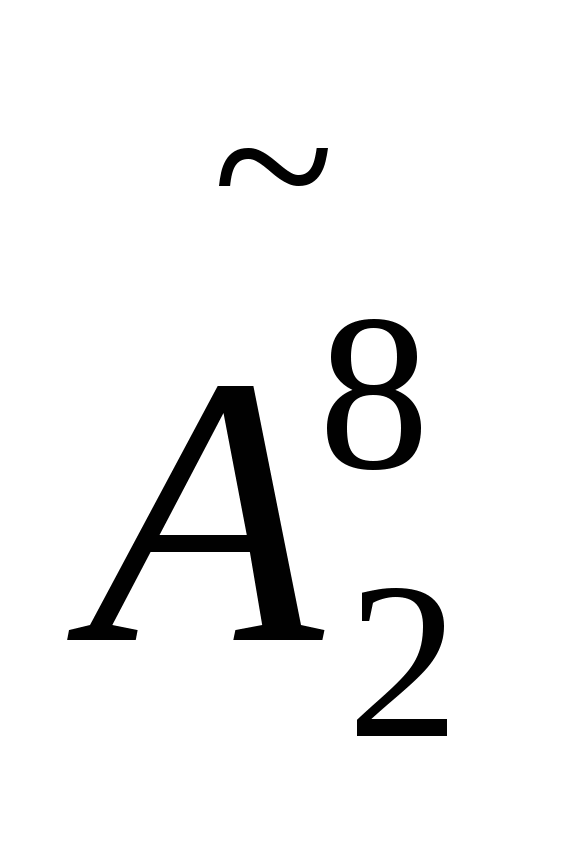 .
.
-
Вычислите
 .
.
-
Сколькими способами можно рассадить 30 учеников в классе?
-
Сколько можно составить сигналов из 9 флажков различного цвета, взятых по 3?
-
Сколькими способами можно 7 различных предметов пронумеровать цифрами 1, 3, 5 и 7?
-
В алфавите племени 4 буквы. Сколько различных трехбуквенных слов может быть в словаре?
-
Сколькими способами можно 10 яблок разложить на 3 тарелки? Яблоки считаются одинаковыми.
-
С помощью треугольника Паскаля найдите четвертый коэффициент в разложении многочлена
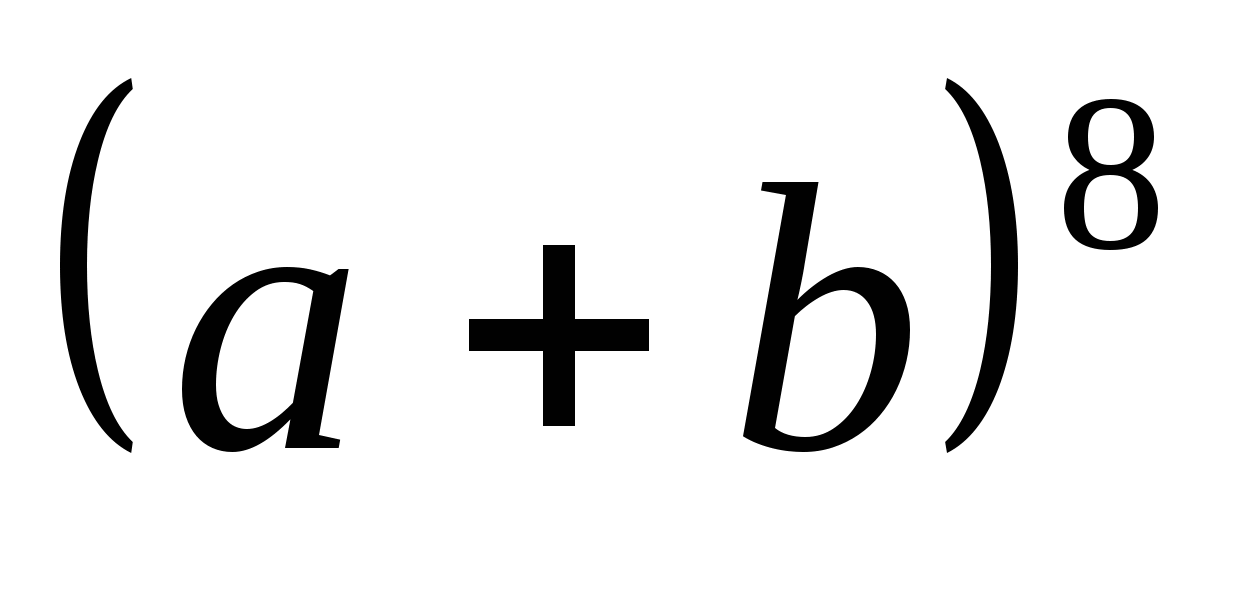 .
.
9. В разложении ![]() пятый член равен 0,336. Найти значение
пятый член равен 0,336. Найти значение ![]() , если сумма биномиальных
коэффициентов равна 1024.
, если сумма биномиальных
коэффициентов равна 1024.
Вариант 3
-
Вычислите
 .
.
-
Вычислите
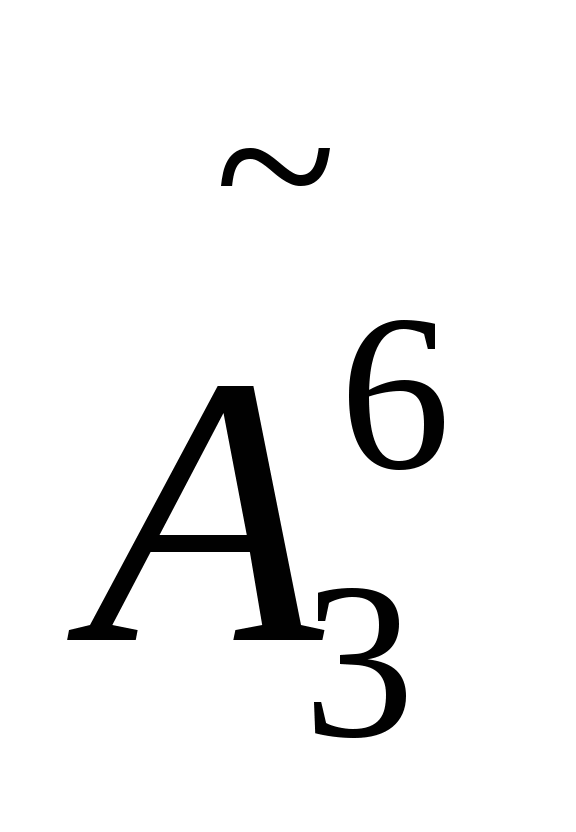 .
.
-
Слово «игрушка» хотят зашифровать, переставляя в нем буквы. Сколькими способами это можно сделать?
-
Набирая номер телефона, абонент забыл последние 3 цифры и, помня лишь, что они различны, решил набрать все возможные варианты. Сколько существует таких комбинаций?
5. Бросают 4 игральные кости. Сколькими способами они могут раскрыться?
6. Сколькими способами из колоды в 36 карт можно выбрать 4 карты так, чтобы среди них не было ни одного туза?
-
Собрание, где присутствуют 30 человек, должно избрать одного делегата из 5 альтернативных кандидатур. Сколькими способами могут распределиться голоса, если каждый подает голос за одного и только одного претендента?
-
С помощью треугольника Паскаля найдите пятый коэффициент в разложении многочлена
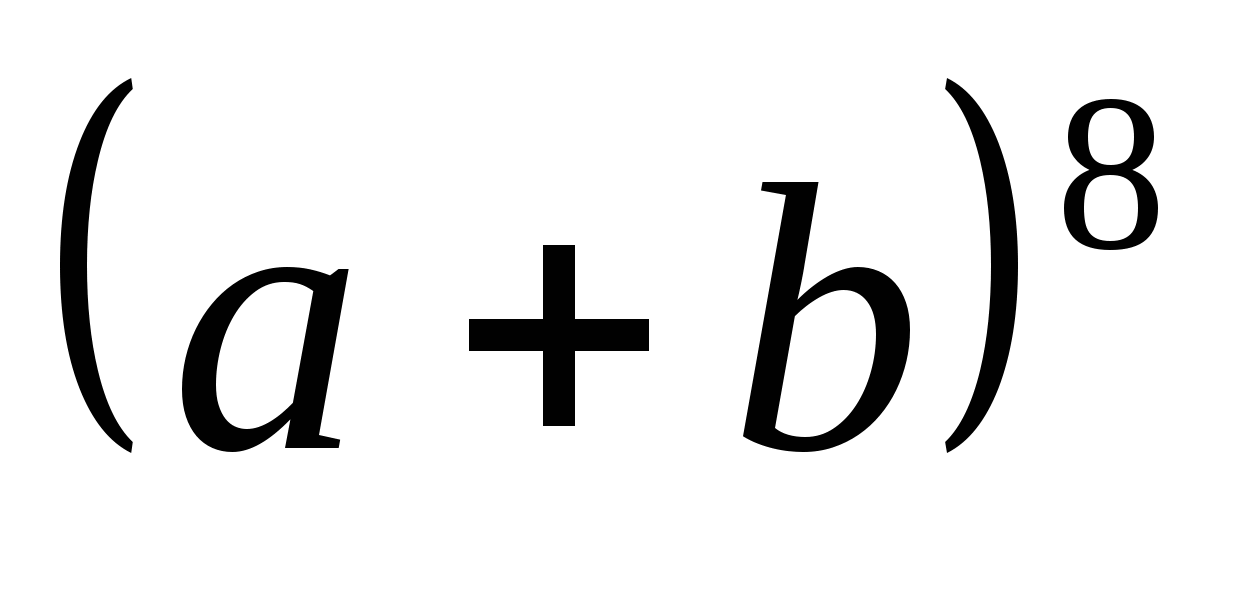 .
.
9. В разложении ![]() десятый член равен 27,5. Найти значение
десятый член равен 27,5. Найти значение ![]() , если сумма биномиальных
коэффициентов равна 4096.
, если сумма биномиальных
коэффициентов равна 4096.
_______________________________________________________________
Вариант 4
-
Вычислите
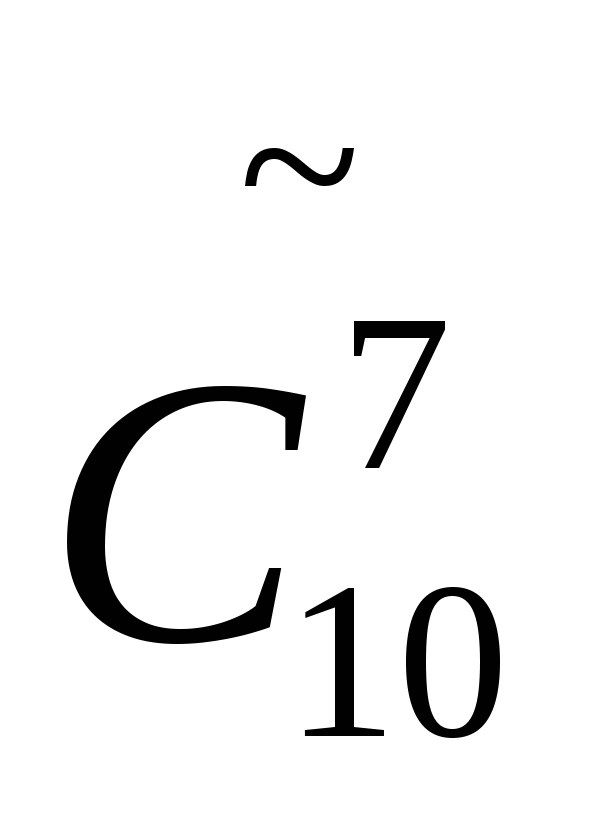 .
.
-
Вычислите
 .
.
3. Сколько различных восьмизначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6, 7 и 8 так, чтобы каждая цифра повторялась 1 раз?
4. Сколькими способами тренер волейбольной команды может из десяти человек, включенных в заявку, составить стартовую шестерку? В волейболе порядок игроков на площадке фиксируется, и его изменение означает изменение стартовой шестерки.
5. Каждую клетку таблицы ![]() можно покрасить в синий или
голубой цвет. Сколько существует способов окраски этой таблицы?
можно покрасить в синий или
голубой цвет. Сколько существует способов окраски этой таблицы?
6. Из 12 солдат требуется назначить патруль в составе 8 солдат. Сколькими способами это можно сделать?
7. Сколькими способами учащиеся 9, 10 и 11 классов могут составить футбольную команду (11 человек) при условии участия в ней представителей каждого класса?
8. С помощью треугольника Паскаля найдите
восьмой коэффициент в разложении многочлена ![]() .
.
9. В разложении ![]() третий член равен 1,89. Найти значение
третий член равен 1,89. Найти значение ![]() , если сумма биномиальных
коэффициентов равна 128.
, если сумма биномиальных
коэффициентов равна 128.