Конспект открытого урока на тему ' Введение декартовых координат в пространстве. Расстояние между точками' (10 класс)

Тема: Введение декартовых координат в пространстве. Расстояние между точками.

Цели урока:

Образовательные: Рассмотреть понятие системы координат и координаты точки в пространстве; вывести формулу расстояния в координатах;

Развивающие: Способствовать развитию пространственного воображения учащихся; способствовать выработке решения задач и развития логического мышления учащихся.

Воспитательные: Воспитание познавательной активности, чувства ответственности, культуры общения, культуры диалога.

Оборудование: Чертежные принадлежности, проектор.

Тип урока: Урок изучения нового материала (2 часа).

Структура урока:

1. Организационный момент.

2. Введение.

3. Сообщение целей урока.

4. Мотивация.

5. Изучение нового материала.

6. Закрепление полученных знаний.

7. Итог урока. Оценивание.

8. Домашнее задание.

9. Литература.

Ход урока

1. Организационный момент. Приветствие.

2. Введение. Сообщение темы урока.

(Слайд 1) Сегодня на уроке мы начинаем изучать четвертый параграф курса геометрии 10 класса "Декартовы координаты и векторы в пространстве".

Какую тему созвучную с темой нашего урока мы изучали в 8 классе? Какое ключевое слово определяют эти две темы? (Координаты).

Координаты на плоскости и в пространстве можно вводить бесконечным числом различных способов.

Решая геометрическую, физическую, химическую задачу можно использовать различные координатные системы: прямоугольную, полярную, цилиндрическую, сферическую. (Показ моделей кристаллической решётки поваренной соли)

(Слайд 2) В общеобразовательном курсе изучается прямоугольная система координат на плоскости и в пространстве. Иначе её называют Декартовой системой координат по имени французского ученого философа Рене Декарта (1596 - 1650) впервые введшего координаты в геометрию.

(Слайд 13) Рене Декарт родился в 1596 г. в городе Лаэ на юге Франции, в дворянской семье. Отец хотел сделать из Рене офицера. Для этого в 1613 г. он отправил Рене в Париж. Много лет пришлось Декарту пробыть в армии, участвовать в военных походах в Голландии, Германии, Венгрии, Чехии, Италии, в осаде крепости гугенотов Ла-Рошали. Но Рене интересовала философия, физика и математика. Вскоре по приезде в Париж он познакомился с учеником Виета, видным математиком того времени - Мерсеном, а затем и с другими математиками Франции. Будучи в армии, Декарт все свое свободное время отдавал занятиям математикой. Он изучил алгебру немецких, математику французских и греческих ученых.

После взятия Ла-Рошали в 1628 г. Декарт уходит из армии. Он ведет уединенный образ жизни с тем, чтобы реализовать намеченные обширные планы научных работ.

Философские взгляды Декарта не соответствовали требованиям католической церкви. Поэтому он переселился в Голландию, где прожил 20 лет, с 1629 по 1649 г., но из-за гонений протестантской церкви в 1649 г. переехал в Стокгольм. Но суровый северный климат Швеции оказался для Декарта губительным, и он умер от простуды в 1650 г.

Декарт был крупнейшим философом и математиком своего времени. В основе его философии лежал материализм. Самым известным трудом Декарта является его "Геометрия". Декарт ввел систему координат, которой пользуются все и в настоящее время. Он установил соответствие между числами и отрезками прямой и таким образом ввел алгебраический метод в геометрию. Эти открытия Декарта дали огромный толчок развитию как геометрии, так и другим разделам математики, оптики. Появилась возможность изображать зависимость величин графически на координатной плоскости, числа - отрезками и выполнять арифметические действия над отрезками и другими геометрическими величинами, а также различными функциями. Это был совершенно новый метод, отличавшийся красотой, изяществом и простотой.

Р. Декарт - французский ученый (1596- 1650)

3. Сообщение цели урока.

(Слайд 3) Сегодня на уроке мы продолжим изучение декартовой системы координат, и покажем, что координаты в пространстве вводятся также просто, как и координаты на плоскости.

4. Мотивация.

В своё время Рене Декарт сказал: "… потомки будут благодарны мне не только за то, что я сказал, но и за то, что я не сказал и тем самым дал им возможность и удовольствие додуматься до этого самостоятельно". Я предоставлю вам возможность и удовольствие разобраться с декартовой системой координат самостоятельно.

5. Изучение нового материала.

(Слайд 4) На основе известного вам материала за 8 класс, мы с вами заполним таблицу. Сделаем сравнительную характеристику.

(На доске нарисована таблица, её необходимо заполнить вместе с учениками.) Рассмотреть основные понятия декартовых координат, формулу расстояния между точками, и попытаться учащимся самим сформулировать основные понятия и формулы в пространстве.

( слайд 5) Для беседы используются рисунки:

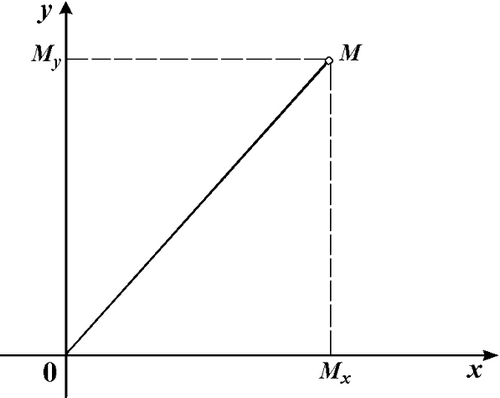
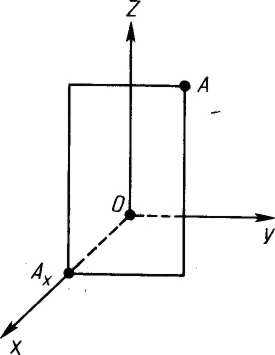
Вопросы для заполнения первой части таблицы.

1. Вспомните и сформулируйте определение известной вам прямоугольной системы координат?

2. Попробуйте сформулировать определение декартовой системы координат в пространстве? (Слайд 6)

3. Назовите оси координат на плоскости? Назовите оси координат в пространстве? Название, какой оси мы не изучали? (Знакомство с новым словом "аппликата") ( Слайд 7)

4. Какие плоскости рассматриваются в планиметрии (в пространстве)?

5. Назовите координату начала координат на плоскости (в пространстве)?(Слайд 8)

6. Какие еще компоненты должна иметь система координат на плоскости и в пространстве? (Направление и единичный отрезок)

7. Как задается координата точки на плоскости и в пространстве? (Слайд 9,10)

Вывод:

Расскажите, как вводится, декартова система координат в пространстве и из чего она состоит?

При беседе построить рисунок фронтально-диметрической проекции осей.

Задания для закрепления

В одной и той же системе координат:

1. Построить точку с заданными координатами А (2; -3).

2. Построить точку с заданными координатами А (1; 2; 3 ).

Рассмотреть построение на доске.

8. Вопросы для заполнения последней строки таблицы.

1. Вспомним и запишем формулу расстояния между точками на плоскости. (Слайд 11)

2. Как бы вы записали формулу расстояния между точками в пространстве? (Слайд 12)

Задания для закрепления

Найти длину отрезка:

1. А (1;2;3;) и В (-1; 0; 5)

2. А (1;2;3) и В (9; 2 ;-3)

6. Закрепление полученных знаний

1. Даны точки A(1; -2; -3), B(2; -3; 0), C(3; 1; -9), D(-1; 1; -12). Вычислить расстояние между 1). А и С, 2). B и D, 3). C и D.

2. Вычислить расстояния от начала координат О до точек A(4; -2; -4), B(-4; 12; 6), C(12; -4; 3), D(12; 16; -15).

3. Доказать, что треугольник с вершинами A(3; -1; 2), B(0; -2; 2), C(-3; 2; 1) равнобедренный.

Во время решения задач - опрос учащихся по предыдущим темам и вновь изученному материалу.

7. Итог урока. Оценивание.

1. Как вводится, декартова система координат? Из чего она состоит?

2. Как определяются координаты точки в пространстве?

3. Чему равна координата начала координат?

4. Назовите формулу расстояния между точками в пространстве.

8. Домашнее задание:

- учить п. 23, 24 стр. 39- 41

- вопросы 1 - 2, задачи 2, 4 стр. 54,

- подготовиться к геометрическому диктанту.

9. Литература.

1. А.В. Погорелов. Учебник 10-11. М. "Просвещение", 2005г.

2. И.С. Петраков. Математические кружки в 8-10 классах. М, "Просвещение", 1987 г.