Учителю
Рабочая программа по алгебре для 8 класса

Рабочая программа по алгебре для 8 класса

Автор публикации: Вассимирская Л.Г.

Дата публикации: 14.11.2014

Краткое описание: Предлагаю вашему вниманию рабочую программу по алгебре для 8 класса, составленную в соответствие с требованиями ФГОС. Реализация данной программы осуществляется с помощью УМК "Алгебра, 8 класс" авторов Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков для 8 класса общеобразоват

предварительный просмотр материала

Муниципальное бюджетное общеобразовательное учреждение Средняя общеобразовательная школа села Шелканово муниципального района Бирский район Республики Башкортостан

СОГЛАСОВАНО

Руководитель РМО учителей математики

______________ / /

СОГЛАСОВАНО

Заместитель директора по УВР

____________/ /

УТВЕРЖДАЮ

Директор МБОУ СОШ с. Шелканово ______________ / /

Приказ от « » 2014 г.

Рабочая программа

по алгебре для 8 класса

на 2014-2015 учебный год

Составила учитель математики

Вассимирская Лилиана Геннадьевна

Рассмотрено на заседании ШМО учителей естественно - математического цикла МБОУ СОШ с. Шелканово

Протокол № от « » 2014 года

Руководитель ШМО ___________ / ./

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Нормативные документы, в соответствии с которыми составлена рабочая программа

- Федеральный компонент государственных образовательных стандартов основного общего образования (приказ Минобрнауки РФ от 05.03.2004г. № 1089)

-Приказ Минобрнауки РФ от 31 марта 2014 года № 253 «Об утверждении федерального перечня учебников, рекомендованных к использованию при реализации имеющих государственную аккредитацию образовательных программ начального общего, основного общего, среднего общего образования»;

-Приказ МБОУ СОШ с. Шелканово от 09.08.2014 г. №83 о перечне учебников, используемых в образовательном процессе в 2014-2015 учебном году;

-Гигиенические требования к условиям обучения в общеобразовательных учреждениях СанПиН 2.4.2.2821 - 10;

-Основная образовательная программа основного (или среднего) общего образования МБОУ СОШ с. Шелканово

-Учебный план МБОУ СОШ с. Шелканово на 2014-2015 учебный год;

-Годовой учебный календарный график с. Шелканово на 2014-2015 учебный год;

-Положение о разработке и утверждении рабочей программы МБОУ СОШ с. Шелканово Муниципального района Бирский район Республики Башкортостан

Сведения о примерной программе по учебному предмету, на основе которой разработана рабочая программа с указанием наименования, автора и года издания

Алгебра. Программы общеобразовательных учреждений, 7 - 9 классы/ Бурмистрова Т.А. - М.: Просвещение, 2010
Алгебра. Рабочие программы. Предметная линия учебников Ю.Н. Макарычева и других,7 - 9 классы/ Н.Г. Миндюк - М.: «Просвещение», 2014 г.

Сведения об УМК

Реализация данной программы осуществляется с помощью УМК «Алгебра, 8 класс» (М.: «Просвещение», 2014) авторов Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова для 8 класса общеобразовательных учреждений

Цель и задачи учебного предмета

Обучение математике в основной школе направлено на достижение следующих целей:

1. В направлении личностного развития:

• развитие логического и критического мышления, культуры речи, способности к умственному эксперименту;

• формирование у учащихся интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта;

• воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;

• формирование качеств мышления, необходимых для адаптации в современном информационном обществе;

• развитие интереса к математическому творчеству и математических способностей.

2. В метапредметном направлении:

• формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества;

• развитие представлений о математике как форме описания и методе познания действительности, создание условий для приобретения первоначального опыта математического моделирования;

• формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности.

3. В предметном направлении:

• овладение математическими знаниями и умениями, необходимыми для продолжения обучения в старшей школе или иных общеобразовательных учреждениях, изучения смежных дисциплин, применения в повседневной жизни;

• создание фундамента для математического развития, формирования механизмов мышления, характерных для математической деятельности.

Общая характеристика учебного предмета

Алгебра нацелена на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира. Одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и др.), для формирования у учащихся представлений о роли математики в развитии цивилизации и культуры. Элементы логики, комбинаторики, статистики и теории вероятностей становятся обязательным компонентом школьного образования, усиливающим его прикладное и практическое значение. Этот материал необходим, прежде всего, для формирования функциональной грамотности - умений воспринимать и анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчеты. Изучение основ комбинаторики позволит учащемуся осуществлять рассмотрение случаев, перебор и подсчет числа вариантов, в том числе в простейших прикладных задачах.

При изучении статистики и теории вероятностей обогащаются представления о современной картине мира и методах его исследования, формируется понимание роли статистики как источника социально значимой информации и закладываются основы вероятностного мышления.

Таким образом, в ходе освоения содержания курса учащиеся получают возможность:

• развить представления о числе и роли вычислений в человеческой практике; сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;

• овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;

• изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;

• развить пространственные представления и изобразительные умения, освоить основные факты и методы планиметрии, познакомиться с простейшими пространственными телами и их свойствами;

• получить представления о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;

• развить логическое мышление и речь - умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;

• сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.

Ценностные ориентиры содержания учебного предмета

Математическое образование играет важную роль как в практической, так и в духовной жизни общества. Практическая сторона математического образования связана с формированием способов деятельности, духовная - с интеллектуальным развитием человека, формированием характера и общей культуры.

Практическая полезность математики обусловлена тем, что ее предметом являются фундаментальные структуры реального мира: пространственные формы и количественные отношения - от простейших, усваиваемых в непосредственном опыте, до достаточно сложных, необходимых для развития научных и технологических идей. Без конкретных математических знаний затруднено понимание принципов устройства и использования современной техники, восприятие и интерпретация разнообразной социальной, экономической, политической информации, малоэффективна повседневная практическая деятельность. Каждому человеку в своей жизни приходится выполнять достаточно сложные расчеты, находить в справочниках нужные формулы и применять их, владеть практическими приемами геометрических измерений и построений, читать информацию, представленную в виду таблиц, диаграмм, графиков, понимать вероятностный характер случайных событий, составлять несложные алгоритмы и др.

Без базовой математической подготовки невозможно стать образованным современным человеком. В школе математика служит опорным предметом для изучения смежных дисциплин. В послешкольной жизни реальной необходимостью в наши дни является непрерывное образование, что требует полноценной базовой общеобразовательной подготовки, в том числе и математической. И наконец, все больше специальностей, где необходим высокий уровень образования, связано с непосредственным применением математики (экономика, бизнес, финансы, физика, химия, техника, информатика, биология, психология и др.). Таким образом, расширяется круг школьников, для которых математика становится значимым предметом.

Для жизни в современном обществе важным является формирование математического стиля мышления, проявляющегося в определенных умственных навыках. В процессе математической деятельности в арсенал приемов и методов человеческого мышления естественным образом включаются индукция и дедукция, обобщение и конкретизация, анализ и синтез, классификация и систематизация, абстрагирование и аналогия. Объекты математических умозаключений и правила их конструирования вскрывают механизм логических построений, вырабатывают умения формулировать, обосновывать и доказывать суждения, тем самым развивают логическое мышление. Ведущая роль принадлежит математике в формировании алгоритмического мышления и воспитании умений действовать по заданному алгоритму и конструировать новые. В ходе решения задач - основной учебной деятельности на уроках математики - развиваются творческая и прикладная стороны мышления.

Обучение математике дает возможность развивать у учащихся точную, экономную и информативную речь, умение отбирать наиболее подходящие языковые (в частности, символические, графические) средства.

Математическое образование вносит свой вклад в формирование общей культуры человека. Необходимым компонентом общей культуры в современном толковании является общее знакомство с методами познания действительности, представление о предмете и методе математики, его отличия от методов естественных и гуманитарных наук, об особенностях применения математики для решения научных и прикладных задач.

Изучение математики способствует эстетическому воспитанию человека, пониманию красоты и изящества математических рассуждений, восприятию геометрических форм, усвоению идеи симметрии.

История развития математического знания дает возможность пополнить запас историко-научных знаний школьников, сформировать у них представления о математике как части общечеловеческой культуры. Знакомство с основными историческими вехами возникновения и развития математической науки, с историей великих открытий, именами людей, творивших науку, должно войти в интеллектуальный багаж каждого культурного человека.

Место учебного предмета в учебном плане в решении общих целей и задач на конкретной ступени общего образования

Согласно Федеральному базисному учебному плану на изучение математики в 8 классе отводится 175 часов из расчета 5 ч в неделю, при этом разделение часов на изучение алгебры и геометрии следующее:

3 часа в неделю алгебры, итого 102 часа; 2 часа в неделю геометрии, итого 68 часов.

Результаты изучения учебного предмета (личностные, метапредметные, предметные)

Изучение математики в основной школе дает возможность обучающимся достичь следующих результатов развития:

1. В направлении личностного развития:

• умение ясно, точно, грамотно излагать свои мысли в устной и письменной форме, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;

• критичность мышления, умения распознавать логически некорректные высказывания, отличать гипотезу от факта;

• представление о математической науке как сфере человеческой деятельности, об этапах ее развития, о ее значимости для развития цивилизации;

• креативность мышления, инициатива, находчивость, активность при решении математических

задач;

• умение контролировать процесс и результат учебной математической деятельности;

• способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений.

2. В метапредметном направлении:

• умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;

• умение находить в различных источниках информацию, необходимую для решения математических проблем, и представлять ее в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации;

• умение понимать и использовать математические средства наглядности (графики, диаграммы, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации;

• умение выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки;

• умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач;

• понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом;

• умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;

• умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера;

• первоначальные представления об идеях и о методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов.

3. В предметном направлении:

предметными результатами изучения предмета «Алгебра» в 8 классе» являются следующие умения:

использовать при решении математических задач, их обосновании и проверке найденного решения знание о:

алгебраической дроби; основном свойстве дроби;
правилах действий с алгебраическими дробями;
степенях с целыми показателями и их свойствах;
стандартном виде числа;
функциях 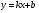, , 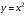, 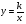их свойствах и графиках;
понятии квадратного корня и арифметического квадратного корня;
свойствах арифметических квадратных корней;
функции 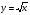, её свойствах и графике;
формуле для корней квадратного уравнения;
теореме Виета для приведённого и общего квадратного уравнения;
основных методах решения целых рациональных уравнений: методе разложения на множители и методе замены неизвестной;
методе решения дробных рациональных уравнений;
основных методах решения систем рациональных уравнений.
сокращать алгебраические дроби;
выполнять арифметические действия с алгебраическими дробями;
использовать свойства степеней с целыми показателями при решении задач;
записывать числа в стандартном виде;
выполнять тождественные преобразования рациональных выражений;
строить графики функций 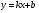, , 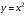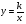и использовать их свойства при решении задач;
вычислять арифметические квадратные корни;
применять свойства арифметических квадратных корней при решении задач;
строить график функции 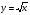и использовать его свойства при решении задач;
решать квадратные уравнения;
применять теорему Виета при решении задач;
решать целые рациональные уравнения методом разложения на множители и методом замены неизвестной;
решать дробные уравнения;
решать системы рациональных уравнений;
решать текстовые задачи с помощью квадратных и рациональных уравнений и их систем;
находить решения «жизненных» (компетентностных) задач, в которых используются математические средства;

создавать продукт (результат проектной деятельности), для изучения и описания которого используются математические средства

Предпочтительные формы контроля

Формами контроля учащихся являются, как традиционные - самостоятельные работы, тестирование, контрольные работы, так и современные - творческие работы, самоанализ и самооценка, наблюдения, проекты, а также внеурочная деятельность учащихся (участие в олимпиадах, творческих конкурсах).

Педагогические технологии, средства обучения, используемые учителем

Данная программа реализуется с помощью разнообразных форм организации учебного процесса, внедрения современных методов обучения и педагогических технологий. Программа предусматривает такую систему организации учебного процесса, основу которой являет собой современный урок с использованием интернет технологий, развивающего обучения, проблемного обучения, обучение развитию критического мышления, личностно - ориентированного обучения. В поддержку современному уроку выступает система консультаций, а также самостоятельная работа учащихся с использованием современных компьютерных технологий.

Осуществление целей данной программы обусловлено использованием в образовательном процессе информационных технологий, диалоговых технологий, программированного обучения, проблемного обучения, личностно-ориентированного обучения. Программа направлена на создание оптимальных условий обучения, исключение психотравмирующих факторов, сохранение психосоматического здоровья учащихся, развитие положительной мотивации к освоению программы, развитие индивидуальности и одарённости каждого ребёнка.

Этнокультурные особенности региона

Стержнем нового ФГОС стали темы: Родины, малой Родины, этнокультурные особенности, которые раскрываются не через конкретные дисциплины, а рассматриваются на каждом предмете и во всех частных темах, где это представляется целесообразным. Чтобы соответствующая работа была успешной, необходимо систематически применять на уроках материал, основанный на этнокультурных особенностях своего региона. Так на уроках математики можно рассматривать задачи, связанные со своим регионом, городом, селом; включать задачи на различные даты, названия природных объектов, растительного и животного мира края. Например, решить пример и, расположив ответы в порядке возрастания, узнать фамилию известного башкирского поэта или писателя; решив задачу, узнать дату основания города и т.д.

Основное содержание учебного предмета

Содержание предмета

Глава 1. Рациональные дроби (24 часа)

Рациональная дробь. Основное свойство дроби, сокращение дробей. Тождественные преобразования рациональных выражений. Функция у =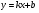 и её график.

Цель: выработать умение выполнять тождественные преобразования рациональных выражений.

Так как действия с рациональными дробями существенным образом опираются на действия с многочленами, то в начале темы необходимо повторить с обучающимися преобразования целых выражений.

Главное место в данной теме занимают алгоритмы действий с дробями. Учащиеся должны понимать, что сумму, разность, произведение и частное дробей всегда можно представить в виде дроби. Приобретаемые в данной теме умения выполнять сложение, вычитание, умножение и деление дробей являются опорными в преобразованиях дробных выражений. Поэтому им следует уделить особое внимание. Нецелесообразно переходить к комбинированным заданиям на все действия с дробями прежде, чем будут усвоены основные алгоритмы. Задания на все действия с дробями не должны быть излишне громоздкими и трудоемкими.

При нахождении значений дробей даются задания на вычисления с помощью калькулятора. В данной теме расширяются сведения о статистических характеристиках. Вводится понятие среднего гармонического ряда положительных чисел.

Изучение темы завершается рассмотрением свойств графика функции у =.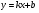

Глава 2. Квадратные корни (19 часов)

Понятие об иррациональных числах. Общие сведения о действительных числах. Квадратный корень. Понятие о нахождении приближенного значения квадратного корня. Свойства квадратных корней. Преобразования выражений, содержащих квадратные корни. Функция у = 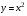, её свойства и график.

Цель: систематизировать сведения о рациональных числах и дать представление об иррациональных числах, расширив тем самым понятие о числе; выработать умение выполнять преобразования выражений, содержащих квадратные корни.

В данной теме учащиеся получают начальное представление о понятии действительного числа. С этой целью обобщаются известные обучающимся сведения о рациональных числах. Для введения понятия иррационального числа используется интуитивное представление о том, что каждый отрезок имеет длину и потому каждой точке координатной прямой соответствует некоторое число. Показывается, что существуют точки, не имеющие рациональных абсцисс.

При введении понятия корня полезно ознакомить обучающихся с нахождением корней с помощью калькулятора.

Основное внимание уделяется понятию арифметического квадратного корня и свойствам арифметических квадратных корней. Доказываются теоремы о корне из произведения и дроби, а также тождество 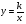=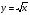, которые получают применение в преобразованиях выражений, содержащих квадратные корни. Специальное внимание уделяется освобождению от иррациональности в знаменателе дроби в выражениях вида 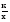, 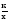. Умение преобразовывать выражения, содержащие корни, часто используется как в самом курсе алгебры, так и в курсах геометрии, алгебры и начал анализа.

Продолжается работа по развитию функциональных представлений обучающихся. Рассматриваются функция у=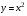, её свойства и график. При изучении функции у=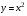, показывается ее взаимосвязь с функцией у = х², где х ≥ 0.

Глава 3. Квадратные уравнения (21 часа)

Квадратное уравнение. Формула корней квадратного уравнения. Решение рациональных уравнений. Решение задач, приводящих к квадратным уравнениям и простейшим рациональным уравнениям.

Цель: выработать умения решать квадратные уравнения и простейшие рациональные уравнения и применять их к решению задач.

В начале темы приводятся примеры решения неполных квадратных уравнений. Этот материал систематизируется. Рассматриваются алгоритмы решения неполных квадратных уравнений различного вида.

Основное внимание следует уделить решению уравнений вида ах² + bх + с = 0, где а 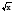0, с использованием формулы корней. В данной теме учащиеся знакомятся с формулами Виета, выражающими связь между корнями квадратного уравнения и его коэффициентами. Они используются в дальнейшем при доказательстве теоремы о разложении квадратного трехчлена на линейные множители.

Учащиеся овладевают способом решения дробных рациональных уравнений, который состоит в том, что решение таких уравнений сводится к решению соответствующих целых уравнений с последующим исключением посторонних корней.

Изучение данной темы позволяет существенно расширить аппарат уравнений, используемых для решения текстовых задач.

Глава 4. Неравенства (19 часов)

Числовые неравенства и их свойства. Почленное сложение и умножение числовых неравенств. Погрешность и точность приближения. Линейные неравенства с одной переменной и их системы.

Цель: ознакомить обучающихся с применением неравенств для оценки значений выражений, выработать умение решать линейные неравенства с одной переменной и их системы.

Свойства числовых неравенств составляют ту базу, на которой основано решение линейных неравенств с одной переменной. Теоремы о почленном сложении и умножении неравенств находят применение при выполнении простейших упражнений на оценку выражений по методу границ. Вводятся понятия абсолютной Погрешности и точности приближения, относительной погрешности.

Умения проводить дедуктивные рассуждения получают развитие как при доказательствах указанных теорем, так и при выполнении упражнений на доказательства неравенств.

В связи с решением линейных неравенств с одной переменной дается понятие о числовых промежутках, вводятся соответствующие названия и обозначения. Рассмотрению систем неравенств с одной переменной предшествует ознакомление обучающихся с понятиями пересечения и объединения множеств.

При решении неравенств используются свойства равносильных неравенств, которые разъясняются на конкретных примерах. Особое внимание следует уделить отработке умения решать простейшие неравенства вида ах > b, ах < b, остановившись специально на случае, когда а<0.

В этой теме рассматривается также решение систем двух линейных неравенств с одной переменной, в частности таких, которые записаны в виде двойных неравенств.

Глава 5. Степень с целым показателем. Элементы статистики (10 часов)

Степень с целым показателем и ее свойства. Стандартный вид числа. Начальные сведения об организации статистических исследований. Сбор и группировка статистических данных. Наглядное представление статистической информации. Круговые диаграммы, полигон, гистограмма.

Цель: выработать умение применять свойства степени с целым показателем в вычислениях и преобразованиях, сформировать начальные представления о сборе и группировке статистических данных, их наглядной интерпретации.

В этой теме формулируются свойства степени с целым показателем. Метод доказательства этих свойств показывается на примере умножения степеней с одинаковыми основаниями. Дается понятие о записи числа в стандартном виде. Приводятся примеры использования такой записи в физике, технике и других областях знаний.

Учащиеся получают начальные представления об организации статистических исследований. Они знакомятся с понятиями генеральной и выборочной совокупности. Приводятся примеры представления статистических данных в виде таблиц частот и относительных частот. Обучающимся предлагаются задания на нахождение по таблице частот таких статистических характеристик, как среднее арифметическое, мода, размах. Рассматривается вопрос о наглядной интерпретации статистической информации. Известные обучающимся способы наглядного представления статистических данных с помощью столбчатых и круговых диаграмм расширяются за счет введения таких понятий, как полигон и гистограмма.

6. Повторение ( 9 часов)

Цель: Повторение, обобщение и систематизация знаний, умений и навыков за курс алгебры 8 класса.

Количество часов, на которое рассчитана рабочая программа, график контрольных и лабораторных работ

Четверть

Количество недель в четверти

Количество часов в неделю

Количество часов в четверти

Количество контрольных работ

I четверть

II четверть

III четверть

IV четверть

Итого в год

102

Особенности класса

Общеобразовательный ( с наличием учащихся по программе VII-го вида)

Внесенные изменения в примерную (авторскую) программу и их обоснование

Требования к уровню подготовки учащихся

В результате изучения курса алгебры в 8 классе учащиеся должны

знать/понимать:

значение математической науки для решения задач, возникающих в теории и на практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа, создания математического анализа, возникновения и развития геометрии;
универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности; вероятностный характер различных процессов окружающего мира;

должны уметь:

выполнять арифметические действия, сочетая устные и письменные приемы; находить значение корня натуральной степени, степени с рациональным показателем, используя при необходимости вычислительные устройства, пользоваться оценкой и прикидкой при практических расчетах;

составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;
выполнять основные действия со степенями с целыми показателями, с многочленами и алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
применять свойства арифметических квадратов корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные уравнения;
решать линейные и квадратные неравенства с одной переменой и их системы;
решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;
изображать числа точками на координатной прямой;
определять координаты точки плоскости, строить точки с заданными координатами; изображать множество решений линейного неравенства;
находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значения аргумента по значению функции, заданной графиком или таблицей;
определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;
описывать свойства изученных функций, строить их графики;
извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы и графики;
решать комбинаторные задачи путем систематического перебора возможных вариантов и с использованием правила умножения;
вычислять средние значения результатов измерений;
находить вероятности случайных событий в простейших случаях;

решать следующие жизненно-практические задачи:

самостоятельно приобретать и применять знания в различных ситуациях;
работать в группах;
аргументировать и отстаивать свою точку зрения;
уметь слушать других; извлекать учебную информацию на основе сопоставительного анализа объектов;
пользоваться предметным указателем энциклопедий и справочников для нахождения информации;
самостоятельно действовать в ситуации неопределенности при решении актуальных для них проблем

Оценка достижения планируемых результатов освоения учебной программы

Оценка письменных контрольных работ обучающихся по математике.

Ответ оценивается отметкой «5», если:

работа выполнена полностью;
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).

Отметка «4» ставится в следующих случаях:

работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
допущены одна ошибка или есть два - три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).

Отметка «3» ставится, если:

допущено более одной ошибки или более двух - трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.

Отметка «2» ставится, если:

допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.

Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.

2.Оценка устных ответов обучающихся по математике

Ответ оценивается отметкой «5», если ученик:

полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
отвечал самостоятельно, без наводящих вопросов учителя;
возможны одна - две неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.

Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:

в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
допущены один - два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.

Отметка «3» ставится в следующих случаях:

неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке обучающихся» в настоящей программе по математике);
имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.

Отметка «2» ставится в следующих случаях:

не раскрыто основное содержание учебного материала;
обнаружено незнание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.

Общая классификация ошибок.

При оценке знаний, умений и навыков обучающихся следует учитывать все ошибки (грубые и негрубые) и недочёты.

3.1. Грубыми считаются ошибки:

незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;
незнание наименований единиц измерения;
неумение выделить в ответе главное;
неумение применять знания, алгоритмы для решения задач;
неумение делать выводы и обобщения;
неумение читать и строить графики;
неумение пользоваться первоисточниками, учебником и справочниками;
потеря корня или сохранение постороннего корня;
отбрасывание без объяснений одного из них;
равнозначные им ошибки;
вычислительные ошибки, если они не являются опиской;
логические ошибки.

3.2. К негрубым ошибкам следует отнести:

неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;
неточность графика;
нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);
нерациональные методы работы со справочной и другой литературой;
неумение решать задачи, выполнять задания в общем виде.

3.3. Недочетами являются:

нерациональные приемы вычислений и преобразований;
небрежное выполнение записей, чертежей, схем, графиков.

Уровневые контрольные работы оцениваются:

«3» - выполнено задание репродуктивного уровня;

«4» - выполнено задание репродуктивного уровня + задание конструктивного уровня;

«5» - выполнено задание репродуктивного уровня + задание конструктивного уровня + задание творческого уровня.

Тестовые работы оцениваются по критериям данного теста.

Календарно-тематический план

№

урока

Сроки проведения

Раздел программы

Тема урока

Кол-во ча-

сов

Характеристика деятельности учащихся*

Примечания

План

Факт

Глава 1. Рациональные дроби

03.09

Рациональные выражения

Объяснять, что такое рациональная дробь; различать целые выражения и дробные; находить область определения дробного выражения

06.09

Рациональные выражения. Допустимые значения переменных

Находить область допустимы

08.09

Основное свойство дроби. Сокращение дробей.

Формулировать основное свойство рациональной дроби и применять его для преобразования дробей.

10.09

Сокращение дробей

Понимать, что значит сократить дробь; знать и применять алгоритм сокращения дроби

13.09

Приведение дробей к новому знаменателю

Применять основное свойство дроби, приводить дроби к новому знаменателю

15.09

Сложение и вычитание дробей с одинаковыми знаменателями.

Выполнять сложение и вычитание рациональных дробей с одинаковыми знаменателями

17.09

Сложение и вычитание дробей с одинаковыми знаменателями.

Выполнять сложение и вычитание рациональных дробей с одинаковыми знаменателями; представлять дробь в виде суммы или разности дробей

20.09

Сложение и вычитание дробей с разными знаменателями.

Выполнять сложение и вычитание дробей с разными знаменателями; уметь находить наименьший общий знаменатель; применять формулы сокращенного умножения

22.09

Сложение и вычитание дробей с разными знаменателями.

Выполнять сложение и вычитание дробей с разными знаменателями; уметь находить наименьший общий знаменатель; применять формулы сокращенного умножения; упрощать выражения

24.09

Сложение и вычитание дробей с разными знаменателями.

Упрощать выражения, применяя правило сложения и вычитания дробей с разными знаменателями

27.09

Обобщение изученного по теме «Сокращение, сложение и вычитание дробей».

Выполнять действия с рациональными дробями, представлять целое выражение в виде многочлена, дробное - в виде отношения многочленов, доказывать тождества.

29.09

Контрольная работа №1 по теме «Сокращение, сложение и вычитание дробей».

Научиться применять приобретенные знания, умения, навыки на практике.

01.10

Анализ контрольной работы. Умножение дробей.

Анализировать ошибки, допущенные в контрольной работе. Выполнять умножение дробей с разными знаменателями, применять формулы сокращенного умножения

04.10

Умножение дробей.

Выполнять умножение дробей с разными знаменателями, применять формулы сокращенного умножения

06.10

Возведение дроби в степень.

Возводить дроби в степень; вывести правило возведения дроби в степень

08.10

Деление дробей.

Выполнять деление дробей с разными знаменателями

11.10

Деление дробей.

Выполнять деление дробей с разными знаменателями

13.10

Деление дробей.

Выполнять деление дробей с разными знаменателями

15.10

Преобразование рациональных выражений.

Выполнять различные преобразования рациональных выражений, доказывать тождества.

18.10

Преобразование рациональных выражений.

Выполнять различные действия с рациональными дробями; представлять ответ в виде несократимой дроби

20.10

Преобразование рациональных выражений.

Доказывать тождества; представлять выражения вв виде дробей; выполнять преобразования рациональных выражений

22.10

Функция y = k/х и её график.

Знать свойства функции y = k/х и уметь строить ее график; использовать компьютер для исследования положения графика в координатной плоскости в зависимости от k

25.10

Задание формулой обратной пропорциональности

Уметь задавать формулой обратную пропорциональность по ее графику или по точке, через которую проходит график обратной пропорциональности

27.10

Контрольная работа №2 по теме «Умножение и деление дробей».

Научиться применять приобретенные знания, умения, навыки на практике.

Глава 2. Квадратные корни

29.10

Анализ контрольной работы. Рациональные числа.

Сравнивать и упорядочивать рациональные числа, выполнять вычисления с рациональными числами; представлять рациональные числа в виде бесконечных периодических дробей и наоборот

05.11

Иррациональные числа.

Знают определение иррационального числа. Иррациональность числа и несоизмеримость стороны и диагонали квадрата. Десятичные приближения иррациональных чисел.

08.11

Квадратные корни. Арифметический квадратный корень.

Находить квадратные корни из неотрицательных чисел

10.11

Нахождение значений арифметического корня

Находить значения арифметических корней; решать простейшие иррациональные уравнения

12.11

Уравнение х² = а.

Решать уравнения x²=a; с помощью графика функции у = х² объяснять количество решений данного уравнения

15.11

Решение уравнений вида х² = а.

Решать уравнения вида х² = а; понимать, от чего зависит количество решений этого уравнения и когда оно не имеет решений

17.11

Нахождение приближённых значений квадратного корня.

Находить приближенные значения квадратного корня

19.11

Функция у = 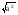и её график.

Строить график функции у = 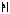и иллюстрировать на графике ее свойства; сравнивать квадратные корни из чисел, используя графическую интерпретацию; располагать числа (кв. корни) в порядке возрастания или убывания

24.11

Квадратный корень из произведения

Доказывать теоремы о корне из произведения и дроби, тождество 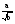= |а|, применять их в преобразованиях выражений

26.11

Квадратный корень из дроби

Доказывать теоремы о корне из произведения и дроби, тождество 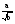= |а|, применять их в преобразованиях выражений

29.11

Квадратный корень из степени.

Применять теоремы о квадратном корне из произведения, дроби и степени при вычислениях

01.12

Контрольная работа №3 по теме «Определение и свойства арифметического корня».

Научиться применять приобретенные знания, умения, навыки на практике.

03.12

Анализ контрольной работы. Вынесение множителя из-под знака корня.

Выносить множитель за знак корня и вносить множитель под знак корня

06.12

Внесение множителя под знак корня

Вносить множитель под знак корня; сравнивать значения выражений, используя данное свойство; располагать числа в порядке возрастания или убывания

08.12

Вынесение множителя из-под знака корня. Внесение множителя под знак корня

Выносить множитель за знак корня и вносить множитель под знак корня. Вносить множитель под знак корня; сравнивать значения выражений, используя данное свойство; располагать числа в порядке возрастания или убывания

10.12

Преобразование выражений, содержащих квадратные корни.

Применение свойств арифметических квадратных корней для преобразования числовых выражений и вычислений

13.12

Преобразование выражений, содержащих квадратные корни.

Применение свойств арифметических квадратных корней для преобразования числовых выражений и вычислений; сокращать дроби

15.12

Освобождение от иррациональности в знаменателе дроби

Освобождаться от иррациональности в знаменателе

17.12

Контрольная работа №4 по теме «Преобразование выражений, содержащих квадратные корни».

Научиться применять приобретенные знания, умения, навыки на практике.

Глава 3. Квадратные уравнения

20.12

Анализ контрольной работы. Определение квадратного уравнения.

Неполные квадратные уравнения.

Работа над ошибками в контрольной работе. Формирование представлений о квадратном уравнении, о старшем коэффициенте, о свободном члене, о приведенном квадратном уравнении, полном квадратном уравнении, неполном квадратном уравнении ,о корне квадратного уравнения

22.12

Решение неполных квадратных уравнений

24.12

Решение квадратных уравнений выделением квадрата двучлена.

Решать квадратные уравнения выделением квадрата двучлена

27.12

Формула корней квадратного уравнения

Формирование представления о дискриминанте квадратного уравнения, о зависимости корней квадратного уравнения от знака дискриминанта; находить корни по формуле

29.12

Решение квадратных уравнений по формуле

Формирование умений решать квадратные уравнения по формуле

17.01

Решение квадратных уравнений по формуле II

Формирование умений решать квадратные уравнения по формуле II (через четверть дискриминанта)

19.01

Решение квадратных уравнений по формуле

Формирование умений решать квадратные уравнения по формуле

21.01

Решение задач с помощью квадратных уравнений.

Решать текстовые задачи, используя в качестве алгебраической модели квадратные уравнения

24.01

Решение задач с помощью квадратных уравнений.

Решать текстовые задачи, используя в качестве алгебраической модели квадратные уравнения

26.01

Теорема Виета.

Находить подбором корни квадратного уравнения; исследовать квадратные уравнения по дискриминанту и коэффициентам

28.01

Применение теоремы, обратной теореме Виета

Формулировать теорему, обратную теореме Виета, применять ее для нахождения корней квадратного уравнения подбором

31.01

Контрольная работа №5 по теме «Квадратные уравнения».

Научиться применять приобретенные знания, умения, навыки на практике.

02.02 04.02

07.02

Решение дробных рациональных уравнений.

Решать дробные рациональные уравнения, сводя решение таких уравнений к решению линейных и квадратных уравнений с последующим исключением посторонних корней.

09.02

Решение задач на движение с помощью рациональных уравнений.

Решать текстовые задачи, используя в качестве алгебраической модели дробные рациональные уравнения

11.02

Решение задач на движение по течению и против течения с помощью рациональных уравнений.

Решать текстовые задачи, используя в качестве алгебраической модели дробные рациональные уравнения

14.02

Решение задач на работу с помощью рациональных уравнений.

Решать текстовые задачи, используя в качестве алгебраической модели дробные рациональные уравнения

16.02

Решение задач на сплавы и растворы с помощью рациональных уравнений.

Решать текстовые задачи, используя в качестве алгебраической модели дробные рациональные уравнения

18.02

Уравнения с параметром.

Формирование представлений о параметре в уравнении и решении таких уравнений

21.02

Контрольная работа №6 по теме «Дробные рациональные уравнения».

Научиться применять приобретенные знания, умения, навыки на практике.

Глава 4. Неравенства

23.02

Анализ контрольной работы. Числовые неравенства.

Работа над ошибками. Уметь проверять неравенства и доказывать их

25.02

Доказательство неравенств

Доказывать неравенства, используя универсальный способ сравнения

28.02

Свойства числовых неравенств.

Формулировать свойства числовых неравенств, обосновывать их, опираясь на координатную прямую, и доказывать алгебраических. Применять свойства неравенств в ходе решений задач

02.03

Применение свойств числовых неравенств

Применять свойства неравенств в ходе решений задач

04.03

Сложение числовых неравенств.

Складывать числовые неравенства.

07.03

Умножение числовых неравенств.

Умножать числовые неравенства

09.03

Применение сложения и умножения числовых неравенств для оценивания выражений

Оценивать выражения, складывая или умножая числовые неравенства

11.03

Погрешность и точность приближения

Использовать аппарат неравенств для оценки погрешности и точности приближения

14.03

Контрольная работа №7 по теме «Свойства числовых неравенств».

Научиться применять приобретенные знания, умения, навыки на практике.

16.03

Анализ контрольной работы. Пересечение и объединение множеств.

Работа над ошибками в контрольной работе. Находить пересечение и объединение множеств.

18.03

Числовые промежутки.

Научится обозначать промежутки, находить их пересечение и объединение

21.03

Решение неравенств с одной переменной.

Решать линейные неравенств; изображать множество решений на координатной прямой

01.04

Решение неравенств с одной переменной.

Решать линейные неравенства; находить целые решения неравенств, его наибольшее или наименьшее решение

04.04

Решение неравенств с одной переменной.

Решать линейные неравенства; находить область определения выражений

06.04

Решение систем неравенств с одной переменной.

Решать системы линейных неравенств; изображать решения на координатной прямой

08.04

Решение систем неравенств с одной переменной.

Решать системы линейных неравенств; находить допустимые значения переменной, составляя системы неравенств

11.04

Решение двойных неравенств

Решать двойные неравенства, уметь записывать их в виде системы линейных неравенств

13.04

Доказательство неравенств.

Уметь доказывать неравенства

15.04

Контрольная работа №8 по теме «Решение линейных неравенств и их систем».

Научиться применять приобретенные знания, умения, навыки на практике.

Глава 5. Степень с целым показателем. Элементы статистки

18.04

Анализ контрольной работы. Определение степени с целым отрицательным показателем.

Знать определение степени с целым отрицательным показателем; находить значение таких степеней

20.04

Вычисление степеней с целым отрицательным показателем

Возводить числа в степень с целым отрицательным показателем

22.04

Свойства степени с целым показателем

Знать свойства степени с целым отрицательным показателем

25.04

Применение свойств степени с целым показателем

Применять свойства степеней с целым отрицательным показателем при выполнении вычислений и преобразовании выражений

27.04

Применение свойств степени с целым показателем

29.05

Стандартный вид числа.

Уметь записывать числа в стандартном виде; использовать запись числа в стандартном виде для выражения и сопоставления размеров объектов, длительности процессов в окружающем мире.

02.05

Контрольная работа №9 по теме «»Степень с целым показателем».

Научиться применять приобретенные знания, умения, навыки на практике.

04.05, 06.05

Анализ контрольной работы. Сбор и группировка статистических данных.

Работа над ошибками в контрольной работе. Приводить примеры репрезентативной и нерепрезентативной выборки; извлекать информацию из таблиц частот и организовывать информацию в виде таблиц частот, строить интервальный ряд

11.05

Наглядное представление статистической информации.

Повторение

13.05

Повторение. Рациональные дроби

Приводить дроби к общему знаменателю; складывать, умножать, и делить рациональные дроби

18.05

Повторение. Квадратные корни и квадратные уравнения.

Применять формулу корней квадратного уравнения и теорему Виета.

16.05

Повторение. Решение задач с помощью квадратных уравнений.

Решать задачи с помощью квадратных уравнений

18.05

Повторение. Решение неравенств и систем неравенств

Знать свойства числовых неравенств.

Решать числовые неравенства и с переменной

20.05

Итоговая контрольная работа

Научиться применять приобретенные знания, умения, навыки на практике.

23.05

Повторение. Решение текстовых задач.

Решать задачи на движение и работу

100

25.05

Повторение. Решение уравнений.

Решать уравнения

101

27.05

Повторение. Преобразование корней

Вносить и выносить множитель под знак корня; преобразовывать корни

102

30.05

Повторение. Элементы статистики

Извлекать информацию из таблиц частот и организовывать информацию в виде таблиц частот, строить интервальный ряд

Перечень учебно-методического обеспечения

Учебный комплект: концепция и программа, учебник, учебное пособие, рабочая тетрадь, учебно-справочное издание, книга для учителя и т.д.

Рабочая программа по алгебре, 7 - 9 классы. Предметная линия учебников Ю.Н. Макарычева и других / Н.Г. Мидюк. - М.: Просвещение, 2014.
Алгебра 8 класс: учеб. для общеобразоват. учреждений / Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова; под ред. С.А. Теляковского. - М.: Просвещение, 2014 г.
Изучение алгебры в 7-9 классах: пособие для учителей. Макарычев Ю.Н., Миндюк Н.Г., Суворова С.Б., Шлыкова И.С. 4-е изд. - М.: «Просвещение» 2011. - 304 с Жохов, В. И. Уроки алгебры в 7 классе : кн. для учителя / В. И. Жохов, Г. Д. Карташева. - М.: Просвещение, 2009.
Элементы статистики и теории вероятностей: Учеб пособие для обучающихся 7-9 кл. общеобразоват. учреждений / Ю.Н. Макарычев, Н.Г. Миндюк; под ред. С.А. Теляковского. -- М.: Просвещение,2001 -2011.

Учебно-практические издания

КИМ. Алгебра (к учебнику Ю.Н. Макарычева и др.) 8 класс/ Мартышова Л.И. - М.: «Вако», 2010
Тесты по алгебре 8 класс: к учебнику Ю.Н. Макарычева и др. /Ю.А. Глазков, М.Я. Гаиашвили. - М.: Издательство «Экзамен», 2011.

Контрольно-диагностические материалы, тесты и т.д

Алгебра: дидакт. материалы для 8 кл. / Л. И. Звавич, Л. В. Кузнецова, С. Б» Суворова. - М.: Просвещение, 2007-2011.
Алгебра. Математические диктанты, 7 - 9 классы/ Конте А.С. - Волгоград: «Учитель», 2007
Алгебра: дидактические материалы для 8 кл. / Ю.Н.Макарычев, Н.Г.Миндюк, Л.Б.Крайнева. - М.: Просвещение, 2010

Учебно-наглядные издания и пособия

Живая математика. Учебно-методический комплект. Версия 4.3. Программа.

Учебно-методические пособия

Уроки алгебры в 8 классе (пособие для учителей к учебнику «Алгебра, 9»), В.И. Жохов, Л.Б. Крайнева, М.: Вербум - М, 2001
Изучение алгебры в 7-9 классах: пособие для учителей. Макарычев Ю.Н., Миндюк Н.Г., Суворова С.Б., Шлыкова И.С. 4-е изд. - М.:

Научно-популярная литература, словари и справочники, атласы, развивающие и дидактические игры и т.д.

Сборник формул по математике (карманный справочник). - М.: Астрель: ACT, 2003.
Наглядный справочник по алгебре и началам анализа, 7-11 класс, Генденштейн Л.Э., Ершова А.П., Ершова А.С., 1997.

Аудио- и видеоприложения

Приложение на электронном носителе к учебнику «Алгебра, 8 класс»

цифровые образовательные ресурсы: Интернет-поддержка, электронные приложения и т.д.)

Сайт ФИПИ;
Сайт газеты «Первое сентября»;
Педсовет, математика
Учительский портал. Математика
Уроки. Нет. Для учителя математики, алгебры, геометрии
Видеоуроки по математике - 6 класс , UROKIMATEMAIKI.RU ( Игорь Жаборовский )
Сайт «Цифровые образовательные ресурсы».
Сайт «Мастерская Савченко Е.М»
http://metaschool.ru/internet-olympiada.php

Перечень материально-технического обеспечения образовательного процесса

Библиотечный фонд, печатные пособия

Журнал «Математика в школе»
Подшивка газеты «Первое сентября», «Математика»
Журнал «Учитель Башкортостана»

Компьютерные и ИКТ средства

Презентации
Операционная система Windows XP
Adobe Reader
Программа «Живая математика»

Технические средства обучения

Компьютер (ноутбук)

Демонстрационные пособия

Демонстрационные таблицы по темам
Портреты известных математиков

Экранно-звуковые пособия

Учебно-практическое и учебно-лабораторное оборудование

Линейка (метровая)
Чертежные угольники (30⁰, 60⁰) и (45⁰, 45⁰)
Транспортиры
Циркули
Доска с магнитной поверхностью и набором приспособлений для крепления таблиц

Учебные игры

Список литературы

Литература, рекомендованная для учителя

Рабочая программа по алгебре, 7 - 9 классы. Предметная линия учебников Ю.Н. Макарычева и других / Н.Г. Мидюк. - М.: Просвещение, 2014.
Алгебра. 8 класс: учеб. для общеобразоват. учреждений / Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова; под ред. С.А. Теляковского. - М.: Просвещение, 2014 г.
Изучение алгебры в 7-9 классах: пособие для учителей. Макарычев Ю.Н., Миндюк Н.Г., Суворова С.Б., Шлыкова И.С. 4-е изд. - М.: «Просвещение» 2011. - 304 с Жохов, В. И. Уроки алгебры в 7 классе : кн. для учителя / В. И. Жохов, Г. Д. Карташева. - М. : Просвещение, 2009.
Элементы статистики и теории вероятностей: Учеб пособие для обучающихся 7-9 кл. общеобразоват. учреждений / Ю.Н. Макарычев, Н.Г. Миндюк; под ред. С.А. Теляковского. -- М.: Просвещение,2001 -2011.
Уроки алгебры в 8 классе (пособие для учителей к учебнику «Алгебра, 9»), В.И. Жохов, Л.Б. Крайнева, М.: Вербум - М, 2001
Алгебра: дидакт. материалы для 7 кл. / Л. И. Звавич, Л. В. Кузнецова, С. Б» Суворова. - М.: Просвещение, 2007-2011.

Литература, рекомендованная для учащихся

Алгебра. 8 класс: учеб. для общеобразоват. учреждений / Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова; под ред. С.А. Теляковского. - М.: Просвещение, 2014 г.
Дидактические материалы по алгебре для 8 класса, Ю.Н.Макарычев, Н.Г.Миндюк, Л.М.Короткова, М.: Просвещение, 2008 год.
Элементы статистики и теории вероятностей: Учеб пособие для обучающихся 7-9 кл. общеобразоват. учреждений / Ю.Н. Макарычев, Н.Г. Миндюк; под ред. С.А. Теляковского. -- М.: Просвещение,2001 -2011.

Дополнительная литература

Миндюк М.Б. Разноуровневые дидактические материалы по алгебре 8 класс. Издательство Дом «Генжер».
КИМы для подготовки к ГИА.
Ганенкова И.С. Математика 8-9 классы «Многоуровневые самостоятельные работы в форме тестов». Издательство Учитель.
Лаппо Л.Д., Попов М.А. Математика. ГИА. Методическое пособие для подготовки. Сборник заданий. М.: Издательство Экзамен.

⇧

⇩