- Учителю
- Разработка занятия кружка по математике для 10 класса
Разработка занятия кружка по математике для 10 класса
Разработка занятия кружка по математике для 10 класса
Тема: « Решение задач для нахождения наибольшего и наименьшего значения некоторых выражений»
Цель: совершенствовать навыки составления и решения уравнений по условию задачи.
Учебная задача: научить учащихся по одному или нескольким условиям задачи получить либо дополнительное уравнение, либо выделить единственное решение из многих возможных.
Развивающие задачи:
-развивать творческую сторону мышления, сообразительность и наблюдательность
- учить школьников самостоятельно осуществлять исследовательскую деятельность
Воспитательная задача: формировать навыки умственного труда - поиск рациональных путей решения.
План занятия:
-
Информационный ввод.
Сообщить учащимся тему занятия, цель
-
Актуализация ЗУН.
Повторение:
1) признаки возрастания и убывания функции;
2) критические точки и экстремумы функции
-
Решение задач.
-
Итог занятия.
Ход занятия:
-
Информационный ввод
Сообщается тема занятия и цель
-
Актуализация ЗУН
Устные упражнения:
-
Укажите промежутки возрастания функции
А) f(x) = 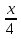 - 2, б) f(x) =
- 2, б) f(x) = 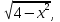 в) f(x) =
в) f(x) = 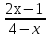 . г) f(x) = х3 + х2 + х
. г) f(x) = х3 + х2 + х
-
Укажите промежутки убывания функции
А) f(x) = -2х2 + 5х -3, б) f(x) = 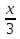 - х3 .
- х3 .
-
При каком значении а функция f(x) = х2 - ах + 3 убывает на промежутке (-
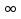 ; 7], возрастает на промежутке [7; +
; 7], возрастает на промежутке [7; +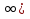 ?
? -
Укажите наибольшее целое отрицательное число, принадлежащее промежутку возрастания функции f(x) = х +
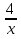
-
Дана функция f(x) = х3 - (а2 - 4)х2. При каких значениях а точка х = 0 является точкой максимума этой функции?
-
Точка х =-2 является точкой максимума функции f(x0) = - х3 - х2 - ах. Найдите значение а и определите в этом случае точку минимума этой функции.
-
Решение задач
На первом этапе учащиеся делятся на 2 группы. Каждой группе предлагается разобрать условие задачи 1
Задача 1. Автомобиль выезжает из пункта А и едет с постоянной скоростью v км/ч до пункта В, отстоящего от пункта А на расстояние 24,5 км/ч . В пункте В автомобиль переходит на равнозамедленное движение, причем за каждый час его скорость уменьшается на 54 км/ч , и движется так до полной остановки. Затем автомобиль сразу же поворачивает обратно и возвращается в А с постоянной скоростью v км/ч. Какова должна быть скорость v, чтобы автомобиль за наименьшее время проехал путь от А до полной остановки и обратно до пункта А указанным выше способом?
И записать в виде выражения:
-
время, за которое автомобиль проезжает расстояние в 24,5 км
-
время в течении которого автомобиль двигался до полной остановки с ускорением 54 км/ч2
-
время, затраченное на обратный путь
-
полное время движения
Затем идет обсуждение выполненного задания, выбирается верное; и учащиеся приходят к заключению, что: «время движения автомобиля от пункта А до полной остановки и обратно является функцией одной переменной 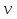 - его скорости на первом участке». После этого оформляется в тетрадях учащихся решение задачи 1:
- его скорости на первом участке». После этого оформляется в тетрадях учащихся решение задачи 1:
Решение:
Подсчитаем время, которое затрачивает автомобиль на весь путь от А до полной остановки и обратно:
-
Расстояние 24,5 км автомобиль проезжает за время t1 =
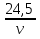 .
. -
Вслед за этим он двигался до полной остановки с ускорением 54 км/ч2 в течение времени t2 =
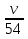 , пройдя при этом расстояние, которое можно определить по формуле для равноускоренного движения: S =
, пройдя при этом расстояние, которое можно определить по формуле для равноускоренного движения: S = 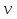 ·t2 -
·t2 - 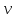 , S =
, S = 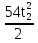 -
- 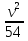 =
= 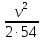 .
. -
Время t3? затраченное на обратный путь, равно t3 =
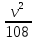 =
= 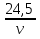 +
+ 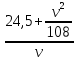 .
.
Поэтому полное время движения автомобиля T = t1 + t2 +t3 = 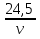 +
+ 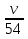 + (
+ (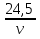 +
+ 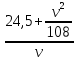 ) =
) = 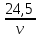 +
+ 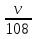
Таким образом, время движения автомобиля от пункта А до полной остановки и обратно является функцией одной переменной 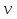 - его скорости на первом участке: T = T(
- его скорости на первом участке: T = T(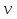 ) =
) =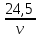 +
+ 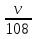
Определим, при каком значении 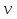 эта функция достигает своего минимума:
эта функция достигает своего минимума:
T'(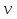 ) =
) = 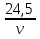 -
- 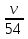 .
.
Необходимым условием экстремума дифференцируемой функции является равенство нулю ее производной 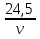 -
- 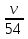 = 0. Находим корни данного уравнения v = ± 42, но учитываем, что
= 0. Находим корни данного уравнения v = ± 42, но учитываем, что 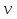 > 0. Получается, что при
> 0. Получается, что при 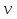 = 42 функция T(
= 42 функция T(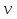 ) имеет минимум, поскольку T'(
) имеет минимум, поскольку T'(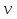 ) > 0 при
) > 0 при 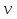 > 42 и T'(
> 42 и T'(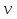 )< 0 при
)< 0 при 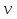 < 42.
< 42.
Итак, при скорости 42 км/ч автомобиль, двигаясь указанным выше способом, затратит на весь путь минимально возможное время.
Ответ: 42 км/ч
На втором этапе каждая группа решает предложенную задачу (1 группа получает задачу 2, 2 группа получает задачу 3).
Решение задач записываются на доске и обсуждаются всем классом.
Задача 2. Три бригады должны выполнить работу. Первая бригада делает в день 200 деталей, вторая - на m деталей меньше, чем первая ( 0< m<200), а третья - на 5 m деталей больше, чем первая. Сначала первая и вторая бригады, работая вместе, выполняют 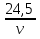 всей работы, а затем все три бригады, работая вместе, выполняют оставшиеся
всей работы, а затем все три бригады, работая вместе, выполняют оставшиеся 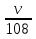
Работы. На сколько деталей в день меньше должна делать вторая бригада, чем первая, чтобы вся работа была выполнена указанным способом как можно скорее?
Решение:
Из условия задачи понятно, что вторая бригада делает в день 200 - m деталей, а третья бригада - 200 + 5 m деталей. Обозначим общее количество деталей, которое нужно сделать через Q. Тогда время всей работы (T) слагается из двух частей:
t1 = 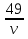 - время работы отдельно первой и второй бригад и t2 =
- время работы отдельно первой и второй бригад и t2 = 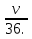 - время совместной работы всех трех бригад. Итак, T = t1 + t2 =
- время совместной работы всех трех бригад. Итак, T = t1 + t2 = 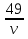 +
+ 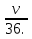 =
= 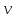 .
.
Таким образом, время всей работы T является функцией (t(m)) только одной переменной m.
Найдем, при каком значении m функция t(m) достигает минимума. Решим уравнение t'(m) = 0. t'(m) = 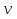 = 0.
= 0.
Откуда m = 125 и при m 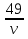 t'(m)
t'(m) 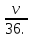 m
m 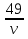 t'(m)
t'(m) 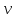
Итак, при m = 125 функция t(m) действительно достигает минимума.
Значит, работа будет выполнена за наименьшее время, если вторая бригада будет делать на 125 деталей в день меньше, чем первая.
Ответ: на 125 деталей меньше.
Задача 3. Между двумя портами, удаленными друг от друга на расстояние 1200 км, с постоянной скоростью курсирует теплоход. Затраты на рейс в одном направлении слагаются из двух частей. Первая часть, связанная с обслуживанием пассажиров, пропорциональна времени нахождения теплохода в пути, а другая, обусловленная стоимостью топлива, пропорциональна кубу скорости движения. Найти скорость, с которой должен идти теплоход, чтобы затраты на рейс были минимальны, если известно, что при скорости 90 км/ч затраты равны 11,61 тыс. руб., причем стоимость обслуживания пассажиров составляет 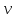 стоимости топлива.
стоимости топлива.
Решение: Обозначим искомую скорость теплохода через 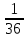 а затраты на рейс через Q. Выразим время движения теплохода в одном направлении : t =
а затраты на рейс через Q. Выразим время движения теплохода в одном направлении : t = 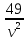 (ч)
(ч)
Из условия задачи имеем : Q = k1t + k2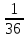 = k1 ·
= k1 ·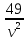 + k2
+ k2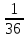 , где k1 и k2 - коэффициенты пропорциональности. Получается, что Q -является функцией только одной переменной
, где k1 и k2 - коэффициенты пропорциональности. Получается, что Q -является функцией только одной переменной 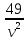
Для определения k1 и k2 используем остальные условия задачи, согласно которым Q(90) = k1 ·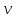 + k2·
+ k2· 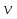 = 11610 и k1 ·
= 11610 и k1 ·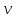 =
= 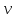 · k2·
· k2· 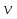 . Получаем систему двух линейных уравнений:
. Получаем систему двух линейных уравнений: 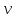
Решая которую, получаем: k1 = 324, k2 = 0,01.
Таким образом, затраты на рейс теплохода при скорости движения 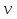 определяются выражением Q(
определяются выражением Q(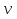
Найдем, при каком значении 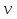 > 0 эта функция достигает минимума. Для этого решим уравнение: Q'(
> 0 эта функция достигает минимума. Для этого решим уравнение: Q'(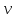 = 0.
= 0.
Q'(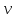 = -
= - 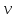 = 0.
= 0.
Получаем, что 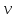 Кроме того, Q'(
Кроме того, Q'(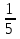 при
при 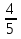 Q'(
Q'(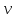 <0 при
<0 при 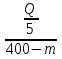 Q(
Q(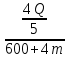
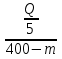
Значит, затраты на рейс будут минимальны при скорости движения 60 км/ч.
Ответ: 60 км/ч.
После обсуждения решения учитель подводит итог занятия, задавая вопрос учащимся: «Можно ли отметить закономерность решения этих задач?»
-
Итог занятия.
-Рассмотрев эти задачи, можно отметить общую закономерность их решения. В каждой задаче сначала выявлялось выражение, изменение которого позволило бы дать ответ поставленный вопрос.
-В первой задаче это было время всего движения, во второй задаче - время выполнения работы, в третьей - затраты на рейс.
-Затем вводился переменный параметр, от которого это выражение зависело. И таким образом , возникала функция, для которой отыскивалось наибольшее или наименьшее значение.
- Во всех рассмотренных случаях для этой цели использовалась производная
Используемая литература:
-
М.В. Лурье, Б.И. Александров. Задачи на составление уравнений. М. Наука, 1990.
-
Е.В. Алтухова и др. Математика. 5-11 классы: уроки учительского мастерства. Волгоград, Учитель, 2007.
-
Б.Г.Зив, П.И. Алтынов. Алгебра и начала анализа. Геометрия.10-11 кл.: Учебн.- метод.пособие. М. Дрофа,1999
8