Урок алгебры для 9 класса «Квадратичная функция»

План-конспект урока алгебры в 9 классе

Тема урока: Квадратичная функция.

Цели урока:

1. Систематизировать знания по теме урока и умение применять их в нестандартной ситуации;

2. воспитание умения самостоятельно организовывать учебную деятельность;

3. контроль ЗУН по теме.

Тип урока: Урок обобщения и систематизации знаний по теме.

1. Организационный момент.

Повторить основные характеристики квадратичной функции ( с последующей записью на доске):

а) Область определения;

б) множество значений;

в) коэффициенты;

г) дискриминант;

д) вершина;

е) ось симметрии;

ж) возрастание и убывание функции;

з) наибольшее и наименьшее значение функции.

2. Систематизация знаний.

1. формула, задающая квадратичную функцию: у = ах² + вх + с, где а≠ 0

2. Графиком функции является парабола. 3)Д(у)=R

4. Е(у)- зависит от расположения вершины и направления ветвей параболы.

5. а>0- ветви параболы направлены вверх;

а<0- ветви параболы направлены вниз.

4. в = 0 - вершина параболы лежит на оси у;

в>0, в<0- вершина параболы может лежать левее или правее оси у, в зависимости от коэффициента Д.

7. с >0, с - 0, с<0 - точка пересечения графика с осью у.

8. Д = в² - 4ас, Д>0- график пересекает ось х в двух точках (х₁ и х₂ );

Д= 0 - вершина параболы лежит на оси х;

Д<0 - график не пересекает ось х.

9) Вершина ( х; у ), где х = -в : (2а), у = ах² + вх + с.

10) Ось симметрии проходит через вершину параболы и параллельно оси у
Она необходима для составления таблицы и построения графика функции.

11. Функция имеет и промежуток возрастания и промежуток убывания, причем вершина входит в каждый из них.

12. Наибольшее или наименьшее значение функция принимает в вершине параболы.

Следует обратить внимание, что из перечисленных характеристик некоторые удобно использовать при работе с графиком, а некоторые при работе с формулой.

3. Актуализация знаний и умений.

На доске записаны 5 формул и дано изображение 3-х графиков квадратичной функции ( см. приложение №1): у = - х² + 2х

у = х² - 4х + 3

у = - х² - 4х

у = х² - 3

у = х² + 2х + 3

Выполнение заданий:

1. Выписать основные характеристики квадратичной функции, заданной графиком №1.

2. Из предложенных формул указать соответствующую графику №1.

3. Квадратичная функция задана формулой у = х -4х + 3- перечислите основные характеристики данной функции.

4. Из предложенных графиков выбрать соответствующий выше указанной формуле.

5. Функции заданы формулами: у = х² + 1

у = х² - 1

у = - х² + 1

у = - х² - 1

графики каких из этих функций не пересекают ось х?

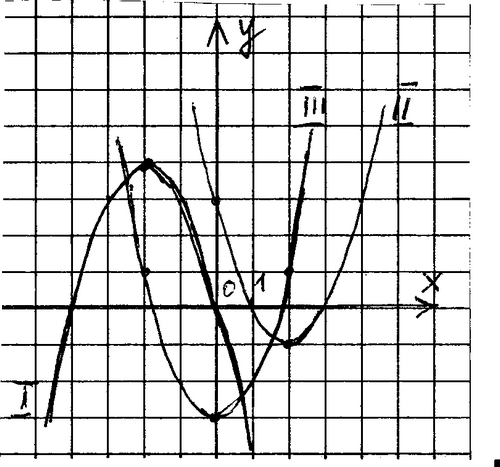
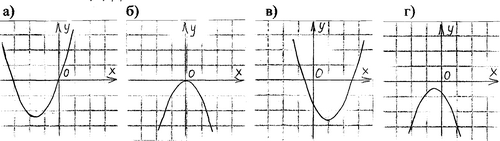
6. Установите соответствие между графиками и знаками коэффициентов:

а) а>0 , с >0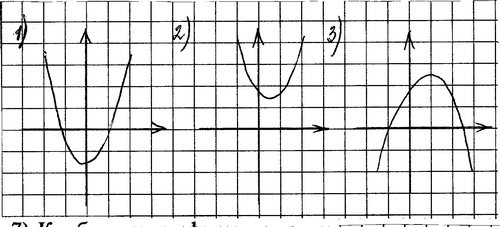

б) а <0 , с >0

в) а >0 , с <0

4. Контроль знаний и умений.

Самостоятельная работа.

Выполнение теста из 5 заданий на 4 варианта.

Взаимопроверка выполненного теста.

Ключ к тесту:

1. в

2 - в

3 - в

4 - в

1

а

б

б

в

2

в

а

г

а

3

г

б

а

в

4

г

г

в

б

5

в

б

в

г

5. Обобщение и итог урока.

Приложение №1.

Тест 1 - вариант

1. Ветви какой параболы направлены вверх?

а) у = - 5 -2х +х² в) у = - х² + 2х +5

б) у = 2х - х² -5 г) у = 5 - 2х - х²

2. Как расположен график квадратичной функции, если а <0, Д =0?

3. Вычислите координаты вершины параболы у = - 4х² + 8х - 7.

а) ( - 1; - 3 ) б) ( 1; 3 ) в) ( - 1; 3 ) г) ( 1; - 3 )

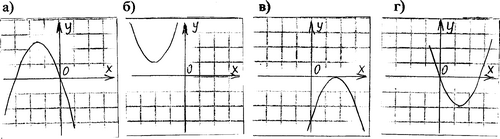
4. График какой квадратичной функции изображен на рисунке?

а) у = 2х² + 4

б) у = - 2х² + 4

в) у = х² - 4

г) у = - х² + 4

5. По графику квадратичной функции определите знаки коэффициентов а, в, с и Д.

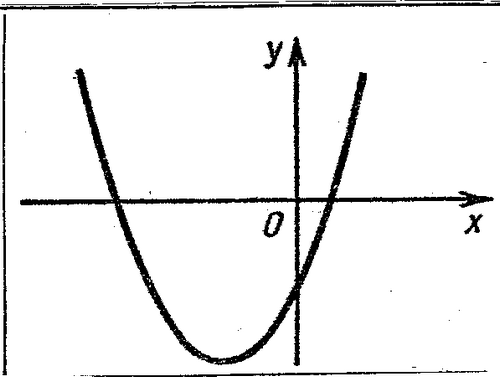
а) а < 0, в <0, с <0, Д <0

б) а <0, в <0, с =0, Д >0

в) а >0, в >0, с <0, Д >0

г) а >0, в >0, с >0, Д =0

Тест 2 - вариант

1. Ветви какой параболы направлены вверх?

а) у = х²+ 2х - 5 в) у = 2х + х² - 5

б) у = 5 + 2х - х² г) у =- 5+ х²- 2х

2. Как расположен график квадратичной функции, если а >0, Д <0?

3. Вычислите координаты вершины параболы у = - х² + 2х + 3.

а) ( - 1; 4 ) б) ( 1; 4 ) в) ( - 1; - 4 ) г) ( 1; - 4 )

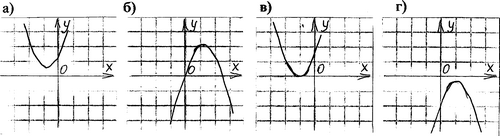
4. График какой квадратичной функции изображен на рисунке?

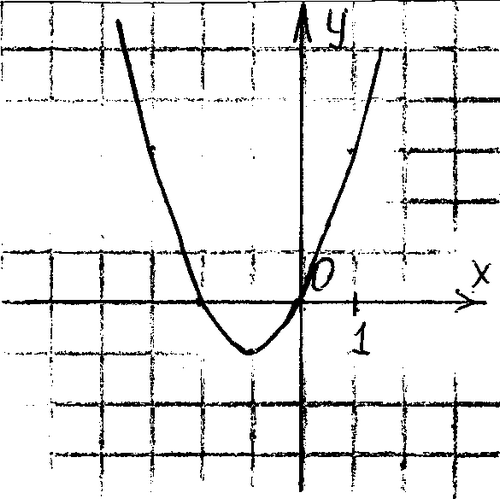
а) у = х² - 2х - 2

б) у = - х² - 2

в) у =- х² + 2

г) у = х² + 2х

5. По графику квадратичной функции определите знаки коэффициентов а, в, с и Д.

а) а < 0, в <0, с =0, Д >0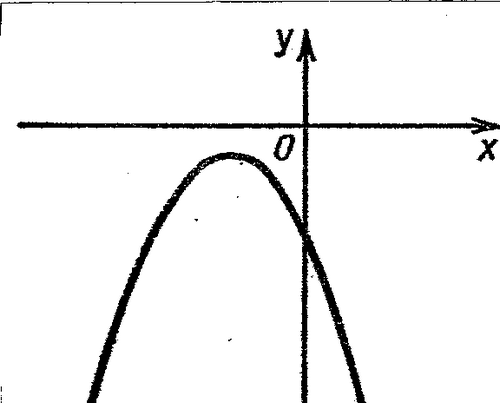

б) а <0, в <0, с <0, Д <0

в) а >0, в >0, с <0, Д >0

г) а >0, в >0, с >0, Д =0

Тест 3 - вариант

1. Ветви какой параболы направлены вверх?

а) у = -3х +4 - х² в) у =- 4х + 3 - х²

б) у =3 + х² + 4х г) у =- х²+ 3х + 4

2. Как расположен график квадратичной функции, если а <0, Д <0?

3. Вычислите координаты вершины параболы у = 2х² - 4х - 6.

а) ( 1; - 8 ) б) ( - 1; 8 ) в) ( 1; 8 ) г) ( - 1; - 8 )

4. График какой квадратичной функции изображен на рисунке?

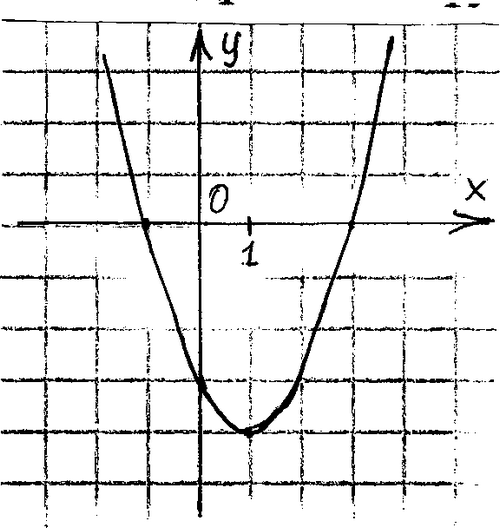
а) у = х² + 2х - 3

б) у = - х² - 2х - 3

в) у = х² - 2х - 3

г) у = - х² + 2х - 3

5. По графику квадратичной функции определите знаки коэффициентов а, в, с и Д.

а) а > 0, в >0, с <0, Д >0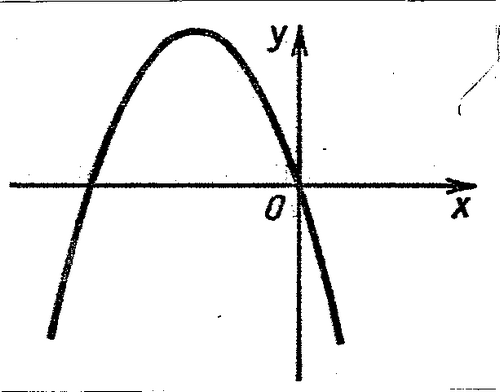

б) а <0, в <0, с <0, Д <0

в) а <0, в <0, с =0, Д >0

г) а >0, в >0, с >0, Д =0

Тест 4 - вариант

1. Ветви какой параболы направлены вверх?

а) у = х² + 5х - 6 в) у = 6х - х² +5

б) у = 6 - 5х + х² г) у = 5 + 6х + х²

2. Как расположен график квадратичной функции, если а >0, Д =0?

3. Вычислите координаты вершины параболы у = х² - 4х - 5.

а) ( -2; 9 ) б) ( 2; 9 ) в) ( 2; -9 ) г) ( - 2; - 9 )

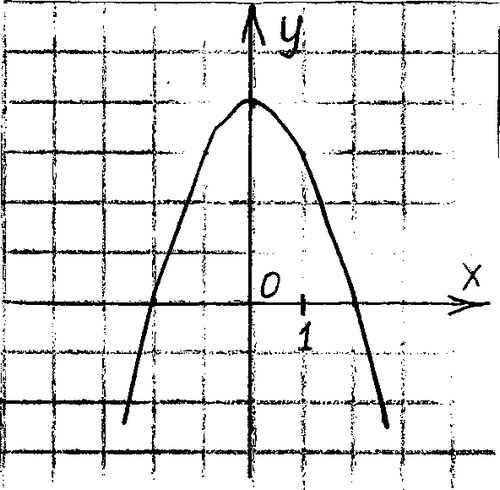
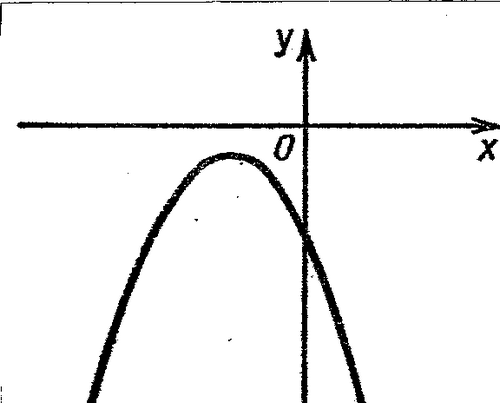
4. График какой квадратичной функции изображен на рисунке?

а) у = х² +2х + 3

б) у = - х² + 2х + 3

в) у = х² - 2х + 3

г) у = - х² - 2х + 3

5. По графику квадратичной функции определите знаки коэффициентов а, в, с и Д.

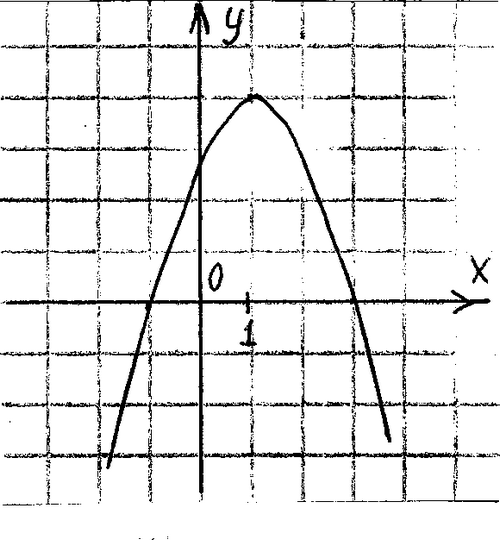
а) а > 0, в >0, с <0, Д >0

б) а <0, в <0, с <0, Д <0

в) а <0, в <0, с =0, Д >0

г) а >0, в >0, с >0, Д =0