- Учителю
- Кейс по теме 'Решение тригонометрических уравнений' (10 класс)
Кейс по теме 'Решение тригонометрических уравнений' (10 класс)
Кейс по теме «Решение тригонометрических уравнений»
По итогам кейса обучающиеся должны освоить следующие общие компетенции:
ОК 1. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.
ОК 2. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития.
ОК 3. Использовать информационно-коммуникационные технологии в профессиональной деятельности.
ОК 4. Работать в коллективе и команде, эффективно общаться с коллегами, руководством, потребителями.
Кейс рассчитан на изучение темы «Решение тригонометрических задач».
Первый урок начинается с того, что каждый обучающийся получает набор учебно-методических материалов, который представляет собой перечень теоретических и практических вопросов, которые будут изучаться в следующей теме. Указывается литература, которой может пользоваться обучающийся. Студентам сообщается, сколько часов отводится на изучение данной темы, по истечении которых будет проведена диагностика знаний по теме.
Обращается внимание обучающихся на различные уровни сложности практических заданий: 1 - материал для устного счета, обязательный уровень подготовки, который может быть оценен только удовлетворительной оценкой, 2 - задания для хорошей и отличной оценки, сложность 3 - творческие задания, требующие применения логического и нестандартного мышления. Студентам предлагается дома просмотреть весь материал по указанной теме. Это позволит им увидеть его место в учебных пособиях, познакомиться с объемом предложенного материала, рассчитать свои силы и время.
На предпоследнем занятии проводится обобщение изученной темы преподавателем, проводится консультация по вопросам, вызвавшим затруднения. Консультировать не обязательно преподавателю - это может делать и любой из обучающихся, у которого предложенный вопрос не вызвал затруднений. Студентам предлагается провести самодиагностику, проставив оценки за каждый этап изученной темы в оценочный лист. Оценочный лист сдается преподавателю для диагностики уровня подготовки обучающихся группы и корректировки работы преподавателя на случай, если затруднения есть у достаточно большого количества обучающихся.
На следующем занятии проводится контроль знаний обучающихся по данной теме. Контроль можно проводить в любой форме, но обязательно предложение задач первого, второго и третьего уровня сложности. Оценку за контрольную работу выставляет уже преподаватель. В идеале - оценка знаний изученной темы обучающимся и преподавателем должны совпадать.
-
Представление кейса
Заканчивая наш колледж, пять обучающихся решили продолжить свое обучение в ВУЗе. Чтобы попасть на бюджетные места заочного отделения Губкинского института (филиала) Университета машиностроения по специальности «Горные машины и оборудование» им необходимо успешно сдать ЕГЭ по математике, а точнее, правильно решить всю часть В и задание С1. Наши студенты хорошо учились и с легкостью справляются с частью В, а вот С1 вызывает у них трудности.
Сегодня мы начинаем изучение новой темы «Решение тригонометрических уравнений». Совместными усилиями мы разработаем рекомендации по решению задач С1, которые помогут нашим выпускникам удачно сдать ЕГЭ.
-
Состав кейса
- Теоремы равносильности при решении тригонометрических уравнений (приложение 1)
- Практические работы (приложение 2)
- Примеры решения тригонометрических уравнений (приложение 3)
- Набор заданий (приложение 4)
- Оценочный лист (приложение 5)
Приложение 1.
Теоремы равносильности при решении тригонометрических уравнений
При решении тригонометрических уравнений необходимо чётко соблюдать теоремы равносильности.
1. Если к обеим частям уравнения 
прибавить выражение 
, не теряющее смысл в области определения, то получим уравнение, равносильное данному.
2. Если обе части уравнения умножить на выражение , отличное от нуля и не теряющего смысл в области определения уравнения, то получим уравнение, равносильное данному.
3. Преобразования левой и правой частей уравнения не должны изменять области определения уравнения.
4. Если при решении произошло расширение области определения уравнения в результате некоторых преобразований (освобождение от знаменателей, сокращение дроби, возведение обеих частей уравнения в одну и ту же чётную степень, при использовании тригонометрических тождеств, левая и правая части которых имеют неодинаковые области определения), то возможно появление посторонних корней. В этом случае необходима проверка найденных решений.
Примеры.
1) 
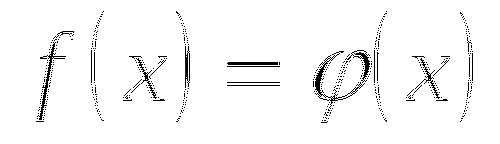
2) 
, 
.
Применение формулы 
расширяет область определения на множество 
. Исходное уравнение равносильно системе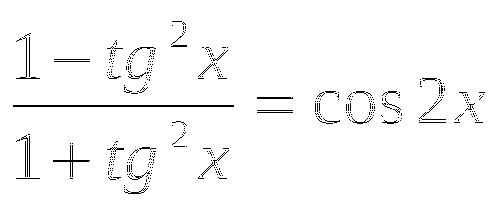 
3) 
. Пусть 
. 
.
.
Если при решении произошло сужение области определения, то возможна потеря решений. Необходимо проверить на какое множество произошло сужение области определения и нет ли среди этого множества корней уравнения. Использование тождества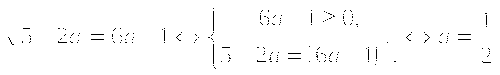 
, 
,
и др. «справа налево» приводит к расширению области определения, а, значит, может привести к появлению посторонних корней; использование этих тождеств «слева направо» ведёт к сужению области определения уравнения, что может привести к потере корней.
Примеры.
1) 
. 
. 
Замена выражения 
выражением 
, выражения 
выражением 
сужает область определения исходного уравнения. Из ОДЗ «выпадают» значения 
.
Подставкой убеждаемся, что также являются решениями данного уравнения
2) 
. . 
.
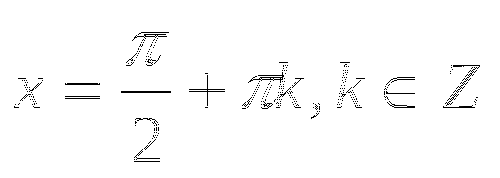
Применение формулы 
сужает область определения уравнения на 
. Проверка показывает, что - корни исходного уравнения.
3) 
. Применение формул 
сужает область определения уравнения и приводит к потере корней вида . Поэтому исходное уравнение равносильно совокупности: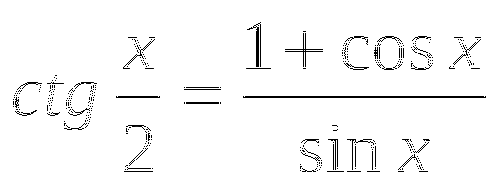
Приложение 2.
Практическая работа по теме «РЕШЕНИЕ ПРОСТЕЙШИХ ТРИГОНАМЕТРИЧЕСКИХ УРАВНЕНИЙ»
Цель: создать содержательные и организационные условия, способствующие формированию общих компетенций через включение в самостоятельную форму работы.
Задачи:
Обучающий компонент: закрепить алгоритм решения простейших тригонометрических уравнений.
Развивающий компонент: обеспечить развитие у обучающихся основ культуры самоуправления учебной деятельность.
Воспитывающий компонент: содействовать формированию компетентностной культуры будущего рабочего в процессе творческого самовыражения, саморегуляции, рефлексии.
Уравнения вида: 
, , 
, 
называются простейшими тригонометрическими уравнениями.
Для решения простейших тригонометрических уравнений применяем формулы:
, 
, 
при 
при 
.
Частные случаи:
при 
, ;
при 
, ;
при 
, .
,
, 
, при 
,
, при .
Частные случаи:
при 
, ;
при 
, ;
при 
, .
, , при
, при
, , при
, , при
Необходимо помнить: 
;
;
;
.
Рассмотрим примеры решения уравнений.
1. 
.
Алгоритм решения:
Используем формулу , .
Подставим в формулу 
, получим 
, .
Найдем 
по таблице: 
.
Записываем ответ: 
, .
2. 
.
Алгоритм решения:
Используем формулу 
, .
Подставим в формулу , получим 
, .
Найдем по таблице: .
Записываем ответ: 
, .
3. 
.
Алгоритм решения:
Используем формулу 
, .
Подставляем в формулу
, получаем 
, .
Находим значение 
по таблице учебника.
Записываем ответ: 
, .
4. 
.
Алгоритм решения:
Используем формулу 
, .
Подставляем в формулу , получаем 
, .
Находим значение по таблице учебника, выполняем необходимые вычисления.
Записываем ответ: 
, .
5. 
Алгоритм решения:
Используем формулу 
, .
Подставляем , получаем 
, .
По таблице находим значение 
.
Записываем ответ: 
, .
6. 
Алгоритм решения:
Используем формулу 
, .
Подставляем , получаем 
, .
По таблице находим значение .
Записываем ответ: 
, .
7. 
.
Алгоритм решения:
Используем формулу 
, .
Подставляем 
, получаем
, .
По таблице находим 
.
Записываем ответ: 
, .
8. 
.
Алгоритм решения:
Используем формулу 
, .
Подставляем , получаем
, .
По таблице находим , выполняем необходимые вычисления.
Записываем ответ: 
, .
Решите самостоятельно уравнения:
1. 
; 
; 
.
2. 
; 
; 
.
3. 
; 
; 
.
Практическая работа по теме «РЕШЕНИЕ ТРИГОНАМЕТРИЧЕСКИХ УРАВНЕНИЙ, СВОДЯЩИХСЯ К ПРОСТЕЙШИМ»
Цель: создать содержательные и организационные условия, способствующие формированию общих компетенций через включение в самостоятельную форму работы.
Задачи:
Обучающий компонент: закрепить алгоритм решения тригонометрических уравнений, сводящихся к простейшим.
Развивающий компонент: обеспечить развитие у обучающихся основ культуры самоуправления учебной деятельность.
Воспитывающий компонент: содействовать формированию компетентностной культуры будущего рабочего в процессе творческого самовыражения, саморегуляции, рефлексии.
Рассмотрим примеры решения уравнений.
1. 
.
Алгоритм решения:
Преобразуем уравнение: переносим в правую сторону, меняя знак
; поделим обе части уравнения на 
, получим 
.
Решаем уравнение, используя формулу: , .
Подставляем 
, получаем: 
, .
Находим значение 
и записываем ответ: 
, .
2. 
.
Алгоритм решения:
Используем формулу: 
, , где 
.
Подставляем в формулу: , получаем: 
, .
Находим значение 
и подставляем в равенство, получаем 
, .
Умножаем обе части уравнения на 3 и записываем ответ: 
, .
3. 
.
Алгоритм решения:
Разделим части уравнения на 
, получим 
.
Решаем уравнение, используя формулу 
, , где 
.
Подставляем в формулу , , получим: 
, .
Находим значение 
: 
, .
Преобразуем полученное равенство: 
переносим в правую часть, меняя знак на противоположный 
, ;
умножаем все равенство на 3,
, .
Записываем ответ: , .
4. 
.
Алгоритм решения:
Преобразуем уравнение, используя формулу 
, 
, получим 
.
Решаем уравнение, используя формулу: 
, , где 
.
Подставляем вместо , 
, получим: 
, .
Находим значение 
и подставляем в равенство 
, .
Разделим обе части равенства на 2 и запишем ответ: 
, .
Решите самостоятельно уравнения:
1. 
; 
; 
.
2. 
; 
; 
.
3. 
; 
; 
.
4. 
; 
.
Практическая работа по теме «РЕШЕНИЕ ТРИГОНАМЕТРИЧЕСКИХ УРАВНЕНИЙ МЕТОДОМ ВВЕДЕНИЯ НОВОЙ ПЕРЕМЕННОЙ»
Цель: создать содержательные и организационные условия, способствующие формированию общих компетенций через включение в самостоятельную форму работы.
Задачи:
Обучающий компонент: закрепить алгоритм решения тригонометрических уравнений методом введения новой переменной.
Развивающий компонент: обеспечить развитие у обучающихся основ культуры самоуправления учебной деятельность.
Воспитывающий компонент: содействовать формированию компетентностной культуры будущего рабочего в процессе творческого самовыражения, саморегуляции, рефлексии.
Рассмотрим примеры решения уравнений.
1. 
.
Алгоритм решения:
Введем новую переменную 
, 
., получаем квадратное уравнение 
.
Решим данное уравнение, используя формулы
, 
. 
; 
; 
; 
.
Получившиеся корни и 
удовлетворяют неравенству . Получаем два простейших тригонометрических уравнения: 
и 
.
Решаем получившиеся уравнения, используя формулу 
, , , 
, ;
, 
, 
.
Записываем ответ: 
, ; 
,
2. 
.
Алгоритм решения:
Перейдем к одной функции, используя формулу 
; 
; 
; 
.
Введем новую переменную 
, , получаем квадратное уравнение 
.
Решаем данное уравнение: 
; 
; 
; 
. Корень не удовлетворяет неравенству .
Решаем простейшее тригонометрическое уравнение 
, используя формулу , , 
, .
Записываем ответ: , .
3. 
.
Алгоритм решения:
Переходим к одной функции используя формулу 
; 
;
Приводим уравнение к общему знаменателю, учитывая, что 
отбрасываем знаменатель 
; 
.
Переходим к новой переменной: 
, получаем уравнение 
.
Решаем квадратное уравнение: 
; 
; 
; 
.
Решаем получившиеся тригонометрические уравнения:
, , ;
, 
, .
Записывает ответ: 
, ; 
, .
Решите самостоятельно уравнения:
1. 
; 
; 
.
2. 
; 
; 
.
3. 
; 
; 
.
Практическая работа по теме «РЕШЕНИЕ ОДНОРОДНЫХ ТРИГОНАМЕТРИЧЕСКИХ УРАВНЕНИЙ»
Цель: создать содержательные и организационные условия, способствующие формированию общих компетенций через включение в самостоятельную форму работы.
Задачи:
Обучающий компонент: закрепить алгоритм решения однородных тригонометрических уравнений.
Развивающий компонент: обеспечить развитие у обучающихся основ культуры самоуправления учебной деятельность.
Воспитывающий компонент: содействовать формированию компетентностной культуры будущего рабочего в процессе творческого самовыражения, саморегуляции, рефлексии.
Рассмотрим примеры решения уравнений.
1. 
Алгоритм решения:
, так как при 
должно выполняться равенство 
.
Следовательно, можно всё уравнение разделить на 
, получаем: 
.
Сократив, получим уравнение: 
.
Так как 
, сделаем замену: 
.
Введём новую переменную , получим уравнение: 
.
; 
; 
.
Решим простейшие тригонометрические уравнения:
; ;
, . 
, .
Записываем ответ: 
, ; 
, .
2. 
.
Алгоритм решения:
Преобразуем правую часть уравнения, используя основное тригонометрическое тождество: 
. Получим уравнение: 
.
Преобразуем данное уравнение: 
.
Решаем полученное уравнение 
.
или 
.
, . При 
.
, .
4. Записываем ответ: 
, ; 
, .
3. 
.
Алгоритм решения:
1. Преобразуем уравнение, используя формулы:
;
;
;
.
.
Получили однородное уравнение.
Решаем получившееся уравнение:
При 
;
; 
;
; 
;
;
;
; 
.
, 
, .
Записываем ответ: , ; 
,.
Решите самостоятельно уравнения:
1. 
; 
.
2. 
; 
.
Практическая работа по теме «РЕШЕНИЕ ТРИГОНАМЕТРИЧЕСКИХ УРАВНЕНИЙ»
Цель: создать содержательные и организационные условия, способствующие формированию общих компетенций через включение в самостоятельную форму работы.
Задачи:
Обучающий компонент: закрепить алгоритм решения различных тригонометрических уравнений.
Развивающий компонент: обеспечить развитие у обучающихся основ культуры самоуправления учебной деятельность.
Воспитывающий компонент: содействовать формированию компетентностной культуры будущего рабочего в процессе творческого самовыражения, саморегуляции, рефлексии.
Пользуясь образцом, решите уравнения
Образец решения уравнения:
.
.
.
.
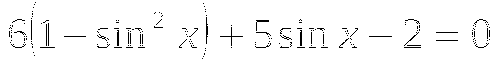- не удовлетворяет условию 
.
Найдём решение уравнения 
с условием (2).
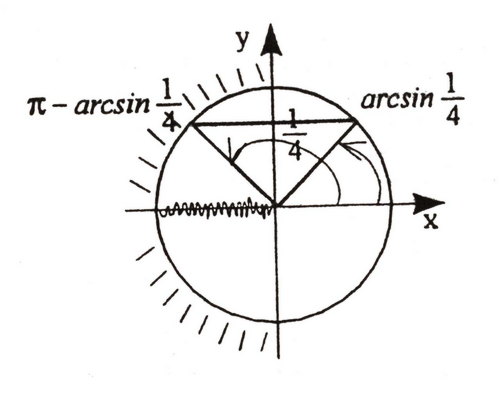Ответ: 
Пользуясь образцом, самостоятельно решите уравнения:
I.
1) 
. 3) 
.
2) 
. 4) 
.
II.
1) 
.
2) 
.
3) 
.
4) 
.
5) 
.
6)
.
7) 
.
III.
1) 
.
2) 
.
Приложение 3.
Примеры решения тригонометрических уравнений
Пример 1. Решить уравнение
.
Решение. Преобразуем сумму синусов в произведение:
,
,
,
,
, 
, 
, .
Ответ. 
, 
.
Пример 2. Решить уравнение
Решение. Раскроем скобки в правой части уравнения, применяя формулу квадрата разности:
.
Применяя формулы, получим
, 
.
Применяя формулу, имеем
,
.
Отсюда или 
. Имеем два решения
, или 
, 
,
, .
Ответ. , ; , .
Пример 3. Решите уравнение 
.
Решение. Применяя формулу, получим
,
,
.
Отсюда 
или 
. Имеем два решения
, 
, 
, ; 
;
, .
Ответ. , ; 
, .
Пример 4. Решить уравнение 
и указать его решения, входящие в 
.
Решение. Воспользуемся формулой приведения, тогда
.
Применяя формулу, имеем
,
.
Отсюда или 
. Имеем два решения
, , 
, ;
, 
, ,
, .
Теперь из этих решений предстоит выбрать те, которые лежат в заданном промежутке. Найдём значения 
и 
при 
, 
и 
, :
; 
; ; 
;
; 
; 
; 
;
; 
; 
; 
.
На промежутке имеется лишь один корень исходного уравнения 
.
Ответ. .
Пример 5. Решить уравнение
.
Решение. Применяя формулу, получим
.
Умножим обе части уравнения на 
:
, 
.
Используя формулу, имеем
, 
.
Отсюда 
или 
. Имеем два решения
, , 
, ;
, , 
, .
Ответ. , ; , .
Пример 6. Решить уравнение 
.
Решение. Используя формулу, получим
, 
.
Обозначая , получим квадратное уравнение 
, откуда 
; 
.
Переходя к переменной 
, имеем два уравнения 
и 
. Решения этих уравнений 
, ; 
Ø.
Ответ. 
, .
Пример 7. Решить уравнение 
.
Решение. 
. Это однородное тригонометрическое уравнение второй степени. Разделим обе части уравнения на . Это можно сделать, так как множество значений , удовлетворяющих уравнению , не являются решением данного уравнения:
,
.
Полагая , имеем 
, откуда 
; 
.
Таким образом, 
или 
. Решения этих уравнений имеют вид 
, , или 
, ; 
, .
Ответ. , ; , .
Пример 8. Решить уравнение
.
Решение. Применяя формулу, получим
,
,
.
Применяя формулу, имеем
,
,
.
Возможны два случая 
или 
. Из первого уравнения , .
Для решения второго уравнения вновь применим формулу:
,
.
Уравнение имеет два решения 
или 
:
, , 
, ;
, 
, 
, .
Ответ. , ; , ; , .
Пример 9. Решить уравнение 
.
Решение. Применяя формулу, получим
.
Полагая 
, причём 
, имеем
, 
Решая квадратное уравнение, получим 
; 
(этот корень не подходит).
Таким образом, 
. Имеем два решения
, 
, или 
, 
, .
Ответ. , ; , .
Пример 10. Решить уравнение 
.
Решение. Исходное уравнение эквивалентно системе
откуда 
При 
получаем, что 
.
Таким образом, подходят только 
; 
, .
Ответ. 
, .
Пример 11. 
.
1) 
2) 
.
3) 
4) 
.
.
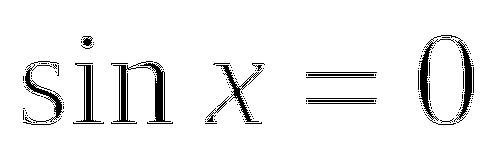
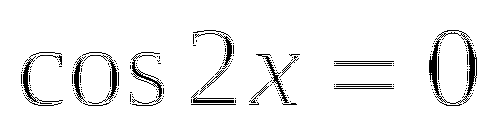
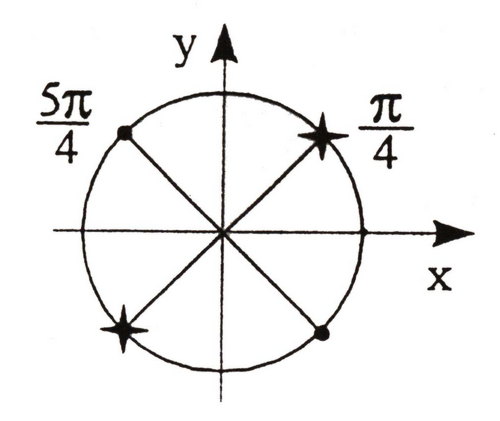
5) 
.
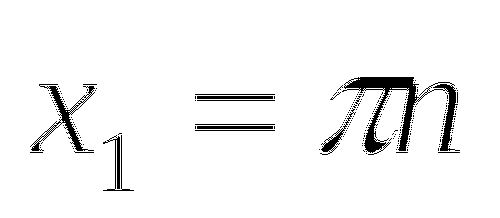
6) . (Разделим на , ).
.
Пример 12. 
.
1) 
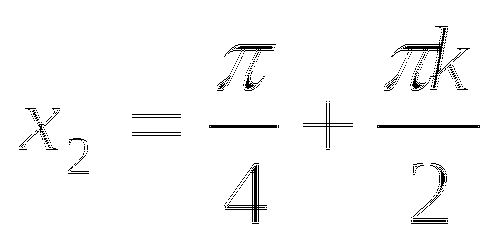
2) 
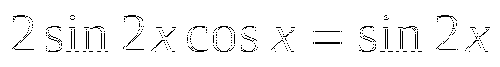
3) 
, 
.
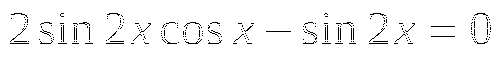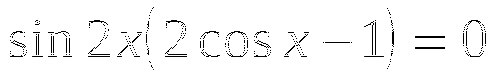Универсальная подстановка.
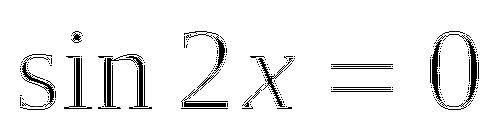. Значения , при которых 
, т.е.
, не является решениями нашего уравнения.
,
4) 
. 
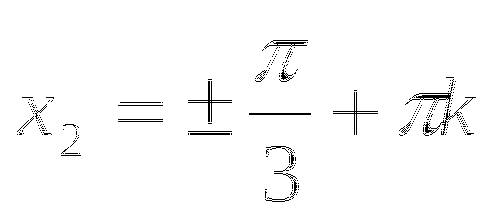
5) .
Метод оценки. 
и 
.
, 
.
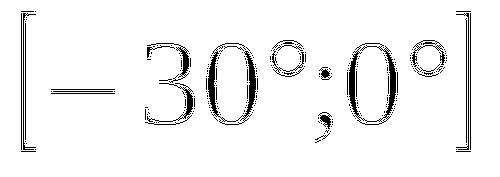
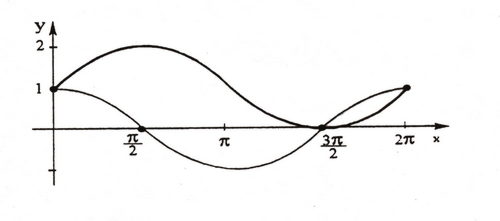
- убывает на 
.
- возрастает на .
Уравнение 
на других корней не имеет.
6) 
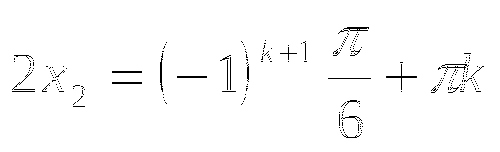
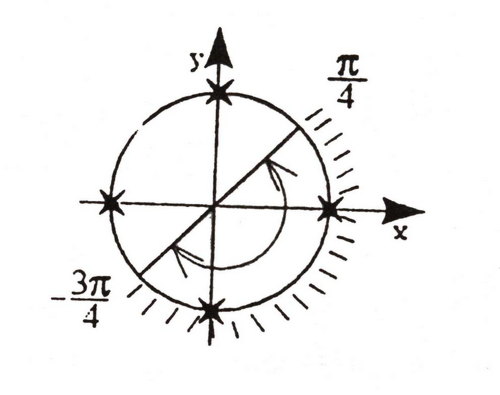
7)
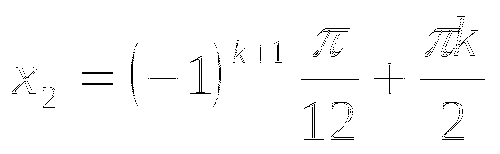
Решение системы:
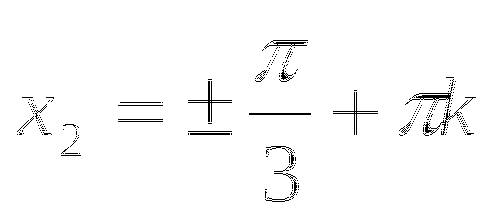
Приложение 4.
Набор заданий
I . Решите простейшие тригонометрические уравнения
1) а) ; б) 
; в) ; г) ;
д) 
; е) 
; ж) 
; г) 
;
2. а)
; б) 
; в) 
;
г) 
; д) 
; е) 
2. Решите уравнения методом разложения на множители
1) 
; 2) 
;
3) 
(преобразовать 
);
4) 
3.Решите уравнения методом введения новой переменной
1) 
; 2) 
;
3) 
; 4) 
.
4. Решите однородные уравнения
1) 
; 2) 
;
3) ;
4) 
;
5) 
.
5. Решите уравнения методом оценки
1) 
; 2) 
;
3) 
; 4) 
.
6. Уравнения, содержащие выражения вида 
, 
. (Применить формул - разность квадратов.)
1) 
; 2) 
;
3) 
.
7. Уравнения, содержащие выражения вида 
, 
.
(Выделить полный квадрат - 
, 
.)
1) 
; 2) 
;
3) 
.
8. Уравнения, содержащие выражения вида 
, 
. (Применить формулу - разность кубов).
1) 
; 2) 
;
3) 
.
9. Уравнение на применение формул 
, 
, 
.
1) 
; 2) 
;
3) 
.
10. Уравнения на применение формулы 
.
1) 
; 2) 
;
3) 
.
11. Решить уравнения и найти корни, расположенные на заданных промежутках. Ответ привести в градусах:
1. 
на 
; 2. на 
;
3. 
на 
; 4. 
на 
;
5. 
на 
; 6. 
на ;
7. 
на 
; 8. 
на 
;
9. 
на 
; 10. 
на ;
11. 
на 
; 12. 
на 
;
13. 
на 
; 14. 
на 
;
15. на .
12. Докажите, что уравнение не имеет корней:
а) 
; б) 
.
13. Решить уравнения и указать количество различных корней, находящихся на заданных промежутках:
1. 
на 
;
2. 
на 
;
3. 
на 
;
4. 
на ;
5. 
на ;
6. 
на 
.
Приложение 5.
Ф.И.
Решение простейших уравнений
Решение уравнений, сводящихся к простейшим
Решение уравнений методом введения новой переменной
Решение однородных тригонометрических уравнений
Самооценка
Оценка преподавателя