Урок по геометрии 'Теорема Пифагора' (8 класс)

ТЕОРЕМА ПИФАГОРА

Цель: ознакомить учащихся с теоремой Пифагора, показать различные способы

ее доказательства, сформировать навыки использования теоремы к

решению задач.

Оборудование: плакаты с иллюстрациями нескольких доказательств теоремы

Пифагора и кроссвордом.

Ход урока:

1. Мотивация учебной деятельности.

Учитель - Начать сегодняшний урок я решила издалека. В 1974 году астрономы попробовали проверить есть ли еще разумные существа во Вселенной. Потенциальным местом, там, где они могут жить, было выбрано звездное скопление в созвездии Геркулеса, которое состоит из сотен тысяч звезд возрастом близко 10 млрд. лет. Астрономы направили сильный радиосигнал, который вместил в себе 1679 различных сообщений. Расшифровав его можно узнать про то, как выглядит человек, как построена наша Солнечная система, какие химические основы нашей человеческой биологии. В послании даже были закодированы некоторые произведения искусства и, естественно, самые значительные достижения науки. Среди базовых достижений науки была закодирована теорема, которую мы должны доказать на уроке - теорема Пифагора.

Поняли ли эту теорему потенциальные жители созвездия Геркулеса, и значима ли она и интересна для них, наши наследники могут узнать через 50 тыс. лет. А поймёте ли теорему Пифагора вы, мы узнаем уже сегодня.

Как говорят «Все течет, все изменяется». И то, что раньше казалось сложным и недосягаемым, со временем станет элементарным. А то, что раньше было не под силу «мужам науки», сегодня делает каждый ученик.

В средние века теорема Пифагора считалась настолько сложной, что ее называли «ослиный мостик», поскольку далеко не каждый мог ее доказать, то есть перейти через «ослиный мостик». Надеюсь, что вы перейдете его без проблем.

Историческая справка

Так в чем же заключается теорема Пифагора?

2. Ознакомление с теоремой.

Учитель: Начнем с формулировки теоремы, которую предложил Пифагор.

Сумма площадей квадрата, построенных на катетах прямоугольного треугольника, равна площади квадрата, построенного на гипотенузе.

Мы с вами будем формулировать теорему так:

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

c² = a ² + b ²

(Рисунок на доске)

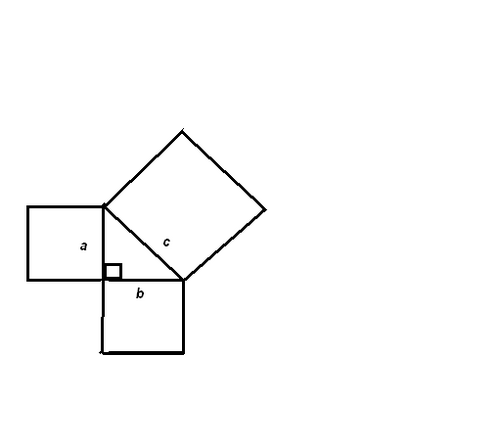
Такое доказательство и является теоремой Пифагора. Считают, что теорему знали намного раньше. Так, за 1500 лет до Пифагора, жители Древнего Египта знали, что треугольник со сторонами 3, 4, 5 - прямоугольный и пользовались этим для построения прямых углов. Такой треугольник называется египетским. Информацию о прямоугольном треугольнике также использовали, когда строили древнеегипетские храмы, храмы Вавилона, Китая, Индии и Мексики.

Как видим, Пифагор не открыл сформулированные в теореме свойства прямоугольного треугольника, а отметил, обобщил и перевел из практической сферы в научную.

Сейчас существует около 150 доказательств этой теоремы. Мы попробуем повторить путь некоторых ученых и доказать теорему Пифагора разными способами.

На доске листы с иллюстрациями некоторых доказательств теоремы Пифагора.

Рассмотрим эти рисунки

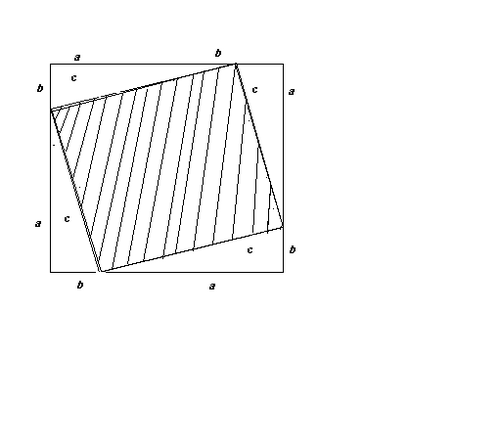
Доказательство:

На чертежах изображено два равных квадрата со сторонами «а + b». Каждый квадрат разбит на части, которые состоят из квадратов и прямоугольных треугольников. В первом случае, если от площади большого квадрата отнять площади четырех прямоугольных треугольников с катетами

« а » и « b », то получим площадь заштрихованного квадрата со стороной « с ».

Во втором случае, если от площади точно такого же квадрата отнять площади четырех прямоугольных треугольников (которые дополняют предыдущие по двум катетам), то площадь двух заштрихованных квадратов равняется « а ² » и « b ² ». Поскольку от равных площадей больших квадратов отняли равные площади прямоугольных треугольников, то останутся равные величины:

c² = a² + b²

Это доказательство, а точнее чертеж, использовали в Древней Индии. А само

доказательство, заключалось в одном слове - СМОТРИ!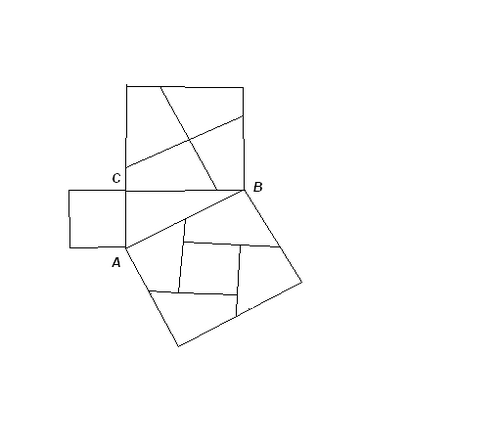

Следующие доказательства основываются на разделении, построенных на катетах квадратов на фигуры, из которых можно сложить квадрат, построенный на гипотенузе. На следующих чертежах показано доказательство одного средневекового багдадского комментатора «Начал» Эвклида.

(Физ. минутка, после неё кроссворд, в котором спрятано слово - косинус.)

Учитель: Для закрепления формулы устно решим упражнения на нахождение третьей стороны треугольника, если известны две другие.

1. а = 3 см, b = 4 cм, с = ? (5)

2. а = 8 см, с = 17 см, b = ? (15)

3. а = 6 см, с = 10 см, b = ? (8)

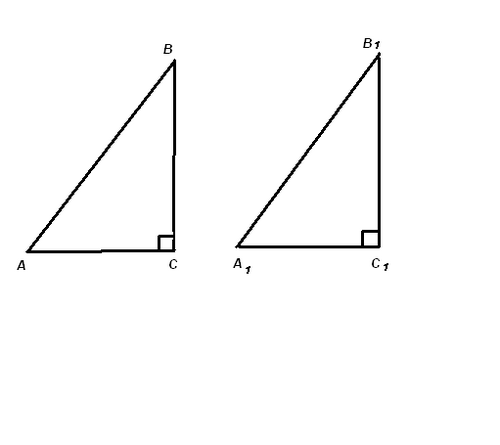
Учитель: Прямоугольные треугольники, стороны которых выражаются целыми числами, называются пифагоровыми (Это треугольники со сторонами 3,4,5; 5,12,13; 8,15,17; 7;24;25).

Считаем, что «ослиный мостик» мы с вами перешли. Осталось от теории перейти к практике. Где и как применялась, применяется и будет применяться теорема Пифагора? Подумаем над этим тоже.

Как гласит легенда, Пифагор был неплохим спортсменом и даже чемпионом олимпийских игр в кулачном бою. Есть версия, что Пифагора сначала не хотели допускать к соревнованиям, говорили, что у него «ни роста, ни силы, ни внешности». «Да, - сказал на это Пифагор, - но я буду наносить удары с математической точностью». Поэтому первая задача, которую будем решать, будет о спорте.

Задача 1. На противоположных берегах реки стоят 2 стрелка. Рост одного - 180

см, другого - 120 см. Ширина реки - 500 см. Оба стрелка одновременно выпустили

стрелы из лука, вошедшие одновременно в мишень на поверхности воды, которая

лежит на прямой, соединяющей ступни стрелков. Найти длину пути стрел и место

нахождения мишени.

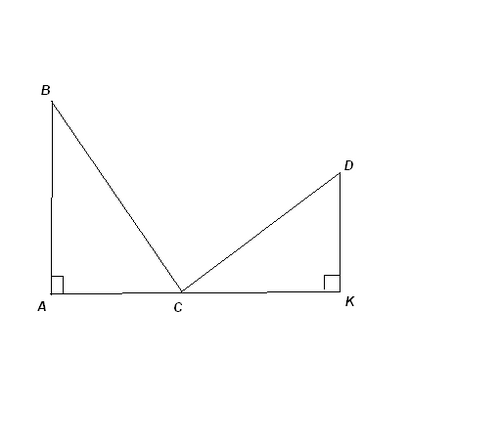
Решение.

Пусть АС = х, тогда КС = 500 - х.

Поскольку ВС = ДС, то 180² + х² = 120² + (500 - х)²

180² +х² = 120² + 250000 - 1000х+х²

1000х = 264400 - 32400

1000х = 232000

х = 232000: 1000

х =232

500 - 232= 268(см); АС=232см; КС = 268см.

180² + 232² = 120² + 268²

Поэтому, ВС = ДС ≈ 293,639(см)

Ответ: АС=232см; КС=268см; ВС = ДС ≈ 293,639 см.

Учитель: Вторая задача тоже не случайная. Так вот - Пифагор оставил о себе

воспоминания и в искусстве, и в литературе. Можно верить, а можно и нет, но

легенды гласят, что Пифагор необычайно хорошо играл на арфе, увлекался стихами

и был неплохим оратором. Поэтому задача - стихотворная.

Задача 2.

Над озером тихим

С полфута размером, высился лотоса цвет.

Он рос одиноко. И ветер порывом

Отнес его в сторону. Нет

Более цветка над водою,

Нашел же рыбак его ранней весною

В двух футах от места, где рос.

Итак, предложу я вопрос -

Как озера вода здесь глубока?

Решение:

Пусть а и b - относительно линия поверхности и дна озера. РL - высота

лотоса над поверхностью, РL = 0,5 , L₁ - положение лотоса после смещения его

ветром, РО = х - глубина озера.

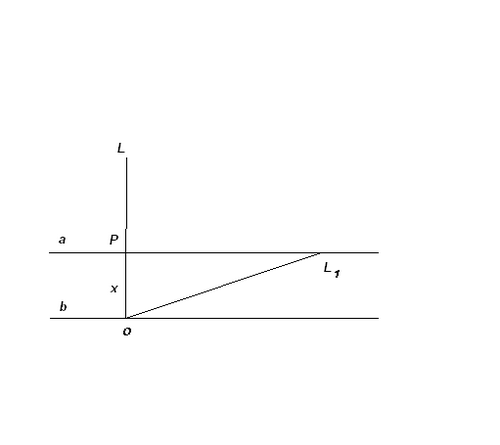
Тогда имеем: ОР² + РL₁² = OL₁²

Поскольку ОL₁ = OL = x + 0,5, то

х² + 4 = (х + 0, 5)²,

х² + 4 = х² + х + 0,25,

х= 3,75

Ответ: глубина озера 3,75 фута.

Учитель: Пифагор, прежде всего, был ученым - математиком. Поэтому

Следующая задача - чисто математическая.

Задача 3. Рассчитать радиус кругового сегмента высотой 4 м, если длина

хорды, которая стягивает дугу сегмента. Равняется 24 м.

Решение.

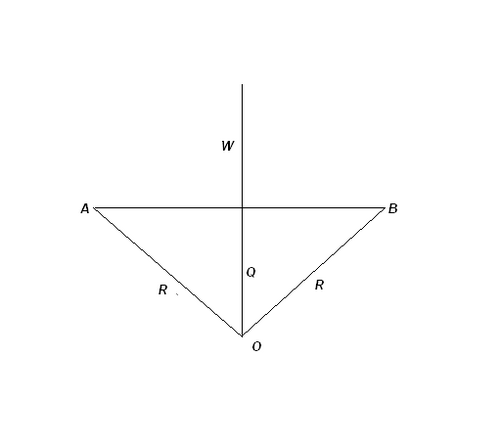
OQ = OP - PQ = R - 4

Из треугольника AQO

OQ² + AQ² = AO²

R = 80.

Ответ: R = 80 метров.

Учитель: Уже при помощи теоремы Пифагора добрались до космоса.

Задача 4. Могут ли увидеть один одного космонавты, которые летят над

поверхностью Земли на высоте 200 км, если расстояние между ними по прямой

равно 2000 км. Радиус Земли приблизительно равен 6000 км.

Решение.

Обозначим через О центр Земли, через К₁, К₂ - положение космонавтов.

Тогда ОР = 6000 км, К₁К₂ - 2000 км.

МК₂ =К₂К₁:2 = 1000,

К₂О = К₂В + ВО = 6200,

МО² =К₂О² - К₂М²,

МО² = 37440000,

ОР² = 6000² = 36000

Поскольку МО > ОР, то космонавты будут видеть один другого.

Учитель: А что ждет теорему Пифагора в будущем? Нет сомнения, что и

тогда она будет иметь большое значение и широкое применение. Где и когда?

Это уже судить не нам. Но подумать над этим можно. Это будет одним из

пунктов вашего домашнего задания. А еще предлагаю вам дома доказать

теорему обратную теореме Пифагора. п.55, с. 128,129- прочитать, №483(б, г);

№484(г, д).

Учитель: Сегодня вы сделали еще один шаг к тому, чтобы считать себя

умным человеком. Даже египетские жрецы, отдавая своих детей на обучение

хотели прежде всего, чтобы они изучали геометрию. А Гиппократ считал, что

для того, чтобы стать врачом Сократа, очутившись на безлюдном острове (по

его мнению) и увидев на песке начерченные геометрические фигуры, радостно

воскликнул «Я вижу геометрические рисунки, значит, я вижу следы людей

разумных».

Вам идти в жизнь, вам доказывать не одну математическую, и не одну

жизненную теорему. Может быть, со временем теорема Пифагора будет

казаться вам до смеха простой. Но сегодня вы преодолели явный рубеж, вы

стали умнее на целую теорему - на теорему Пифагора.

Историческая справка
к открытому уроку по геометрии 8 класс

Бинарный урок

Теорема Пифагора

Учитель. Перед изучением теоремы вспомним ее автора. Останавливаться надолго на его

биографии не будем. Напомню лишь, что родился он на острове Самос около 500 г. до н.э., получил прекрасное образование. Много путешествовал по Египту, провел там 22 года, изучал различные науки. Хорошо овладев знаниями египтян, в том числе и математикой, как пленный, попал в Вавилон, где провел 12 лет, изучая астрономию и астрологию. Предания приписывают Пифагору посещение Индии. После плена переселился в Северную Италию и в Кротоне (греческой колонии) открыл известную Пифагорейскую школу, которая действовала почти 30 лет. Школа Пифагора, или, как ее еще называют, пифагорейский союз, была одновременно и философской школой, и политической партией, и религиозным братством. Статут пифагорейского союза был очень суровым. Каждый, кто вступал в него, отказывался от личной собственности в пользу союза, обязывался не проливать крови, не употреблять мясной пищи, беречь тайну учения своего учителя. Членам школы запрещалось обучать других за вознаграждение. В конце 5 века до н.э. в Греции и ее колониях прокатилась волна демократического движения. Победила демократия и в Кротоне. Пифагор вместе с учениками оставляет Кротон и уезжает в Тарент, а затем в Метапонт. Прибытие пифагорейцев в Метапонт совпало со вспышкой там народного восстания. В одной из ночных стычек погиб почти 90-летний Пифагор. Его школа прекратила свое существование. Ученики Пифагора, спасаясь от преследований, расселились по всей Греции и ее колониям. Добывая себе средства к существованию, они организовывали школы, в которых преподавали главным образом арифметику и геометрию. Сведения об их достижениях содержатся в сочинениях позднейших ученых - Платона, Аристотеля и др.

Самым значительным вкладом развития этой школы в математику являются: несоизмеримые отрезки, теорема о сумме углов треугольника, учение о правильных многогранниках и т.д. Но самым известным открытием - считается именно теорема Пифагора.

Пребудет вечной истина, как скоро

Ее познает слабый человек!

И ныне теорема Пифагора

Верна, как и в его далекий век.

Обильно было жертвоприношенье

Богам от Пифагора. Сто быков

Он отдал на закланье и сожженье

За света луч, пришедший с облаков!

Легенда говорит, что когда Пифагор сформулировал и доказал теорему, то принес в жертву богам 100 быков, откуда и пошло второе название теоремы - «гекатомба» (сто быков).

(Далее следует объяснение учителя математики различных доказательств теоремы Пифагора)

Учитель. Мы рассмотрели с вами доказательство теоремы Пифагора геометрическими методами. Докажем ее алгебраическим способом. Предварительно вспомним слово, которое «спрятано» среди слов кроссворда.

(Кроссворд и вопросы к нему кладут каждому на парту).

1. Название прямоугольного треугольника со сторонами 3, 4, 5?

2. Ученый, именем которого названа теорема про сумму квадратов катетов прямоугольного треугольника?

3. Остров, на котором родился этот ученый?

4. Катет, который не лежит напротив данного угла?

5. Там Пифагор прожил 12 лет?

6. Сторона прямоугольного треугольника, которая лежит против прямого угла?

7. Количество быков, принесенное Пифагором в жертву богам после доказательства теоремы?

(Далее следует закрепление изученного на уроке геометрии материала)