План урока Комплексные числа

Раздел 1. Развитие понятия о числе.

Тема 1.1. Комплексные числа.

Вид занятия: Усвоение знаний на основе имеющихся.

Тип урока: Аудиторное теоретическое занятие.

Цель занятия: формирование умений применять математические понятия в различных областях науки и жизни.

Задачи занятия:

Образовательные (обучающие): обобщить понятие действительного числа, рассмотреть множество иррациональных чисел, множество действительных чисел; рассмотреть правила выполнения действий с бесконечными десятичными дробями; сформировать умения применять математические понятия в других областях жизни, научить применять полученную модель на практике.

Развивающие: развить умения находить нужную литературу, обрабатывать информацию, выполнять и оформлять научно-исследовательскую работу, формировать «ключевые компетенции».

Воспитательные: обучить навыкам: планирования деятельности, работы в оптимальном темпе, подведения итогов; развить умения оценивать свои способности, свое положение в группе, контактировать с товарищами; вызвать чувства ответственности и сопереживания; воспитывать духовно - нравственно на примере жизни выдающихся математиков.

Технологии обучения: развитие мышления, полное усвоение знаний, интерактивное обучение.

Методы и приемы обучения: эффективная лекция, объяснительно - иллюстративное, актуализация личностного опыта.

Методическое оснащение урока:

• Источники информации: программа дисциплины, план урока, литература для преподавателя,

• Оборудование: мель, доска.

• Материалы для познавательной деятельности обучающегося: задания для выполнения на уроке, цветные ручки.

ПЛАН УЧЕБНОГО ЗАНЯТИЯ:

1. Организационный момент.

2. Мотивация.

3. Сообщение темы, постановка целей и задач занятия совместно с обучающимися. Составление плана изучения темы.

4. Самостоятельная работа студентов на занятии.

5. Первичная проверка и закрепление изученного материала.

6. Подведение итогов занятия (анализ и оценка успешности достижения

цели, результативность занятия).

7. Рефлексия.

8.Задание на дом, инструктаж по его выполнению.

Ход занятия

1.Организационный момент (5 мин): взаимные приветствия преподавателя и студентов; фиксация отсутствующих в учебном журнале; проверка внешнего состояния кабинета; проверка подготовленности студентов к занятию, их настроя на работу; организация внимания и внутренней готовности.

2.Мотивация

Дейл Карнеги утверждает: «… на свете есть только один способ побудить людей что-то сделать - заставить человека захотеть это сделать.

3.Сообщение темы, постановка целей и задач занятия совместно с обучающимися. Составление плана изучения темы (или ознакомление с планом)

(45 мин)

Тема урока: Комплексные числа.

План изучения темы:

1. Действительные числа.

2. решение задач.

Определение. Запись комплексного числа в виде называется алгебраической формой комплексного числа.

Сложение комплексных чисел. Суммой двух комплексных чисел и называется комплексное число, определяемое равенством

(1)

Вычисление комплексных чисел. Разностью двух комплексных чисел и называется такое комплексное число, которое, будучи сложенным с , дает число :

(2)

Пример. Найти сумму и разность комплексных чисел и .

Решение.

.

.

Умножение комплексных чисел. Произведением комплексных чисел в алгебраической форме и называется комплексное число, определяемое равенством:

. (3)

Это формула получено путем перемножения двучленов и :

Например:

.

Замечание. Произведением сопряженных чисел и в силу равенства (3) выражается так: или

Деление комплексных чисел. Делением комплексных чисел определяется как обратное умножению.

Практически деление комплексных чисел выполняется следующим образом: чтобы разделить на , умножаем числитель и знаменатель на число, сопряженное знаменателю (т.е. на ). Тогда делителем будет действительное число; разделив на него действительную и мнимую часть делимого, получим частное

.

Пример. Выполните деление .

Решение:

Определение. Тригонометрической формой ненулевого комплексного числа называется выражение , где - модуль комплексного числа (), а угол

Произведение комплексных чисел тригонометрической форме.

Произведением двух комплексных чисел и есть такое комплексное число, модуль которого равен произведению модулей перемножаемых чисел, а аргумент равен сумме аргументов сомножителей:

Возведение в степень.

Правило умножение комплексных чисел распространяется на любое конечное число сомножителей.

В частности, если - целое положительное число.

, то .

Деление комплексных функций в тригонометрической форме.

Модуль частного двух комплексны чисел, заданных тригонометрической форме, равен частному модулей делимого и делителя; аргумент частного равен разности аргументов делимого и делителя.

Пример. Найти произведение и частное комплексных чисел:

и .

Решение.

4. Самостоятельная работа:

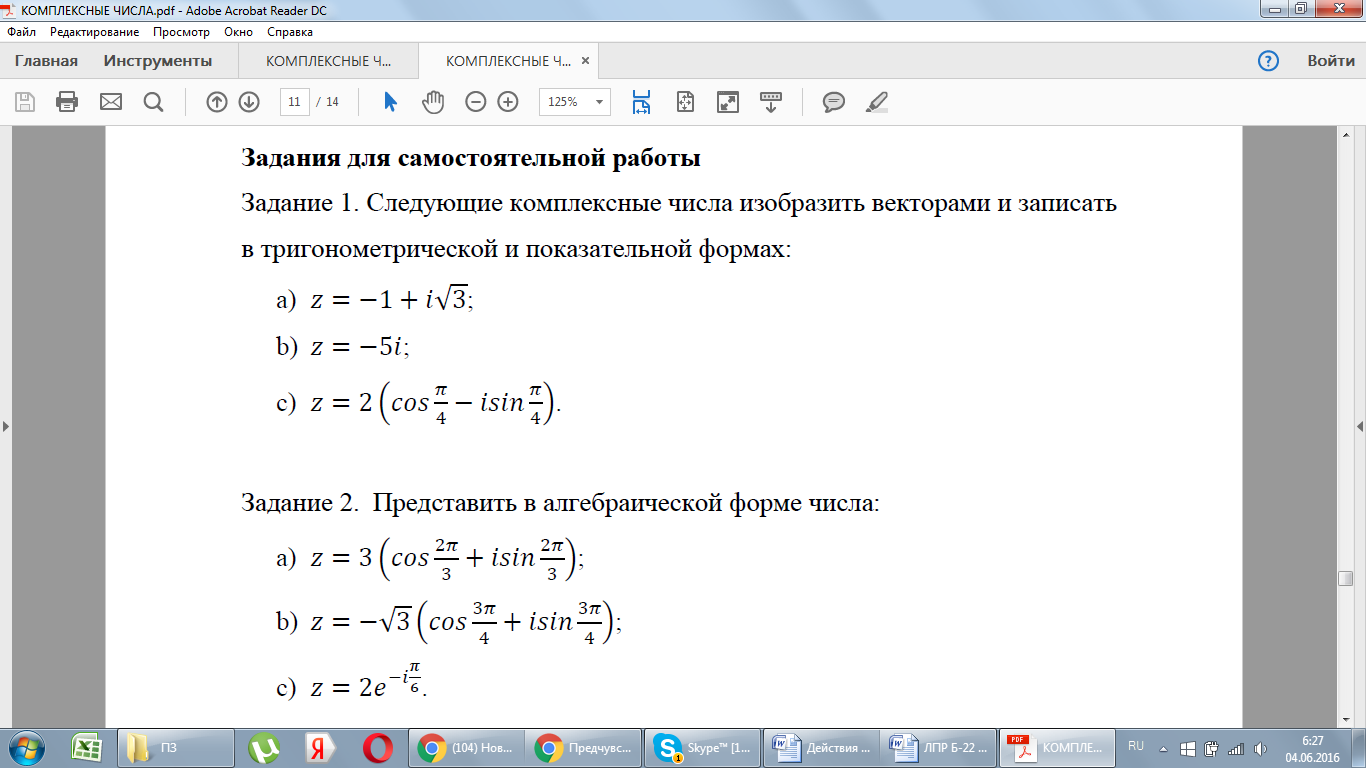
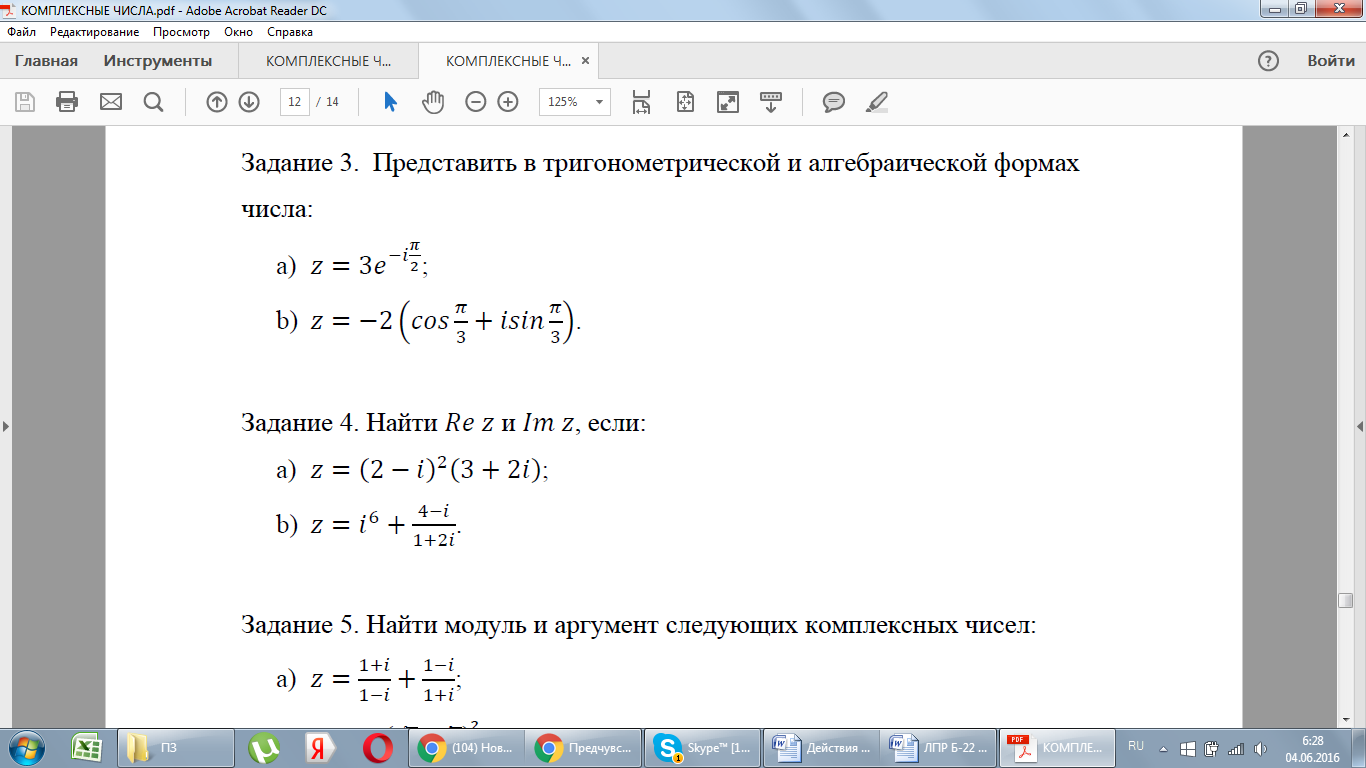
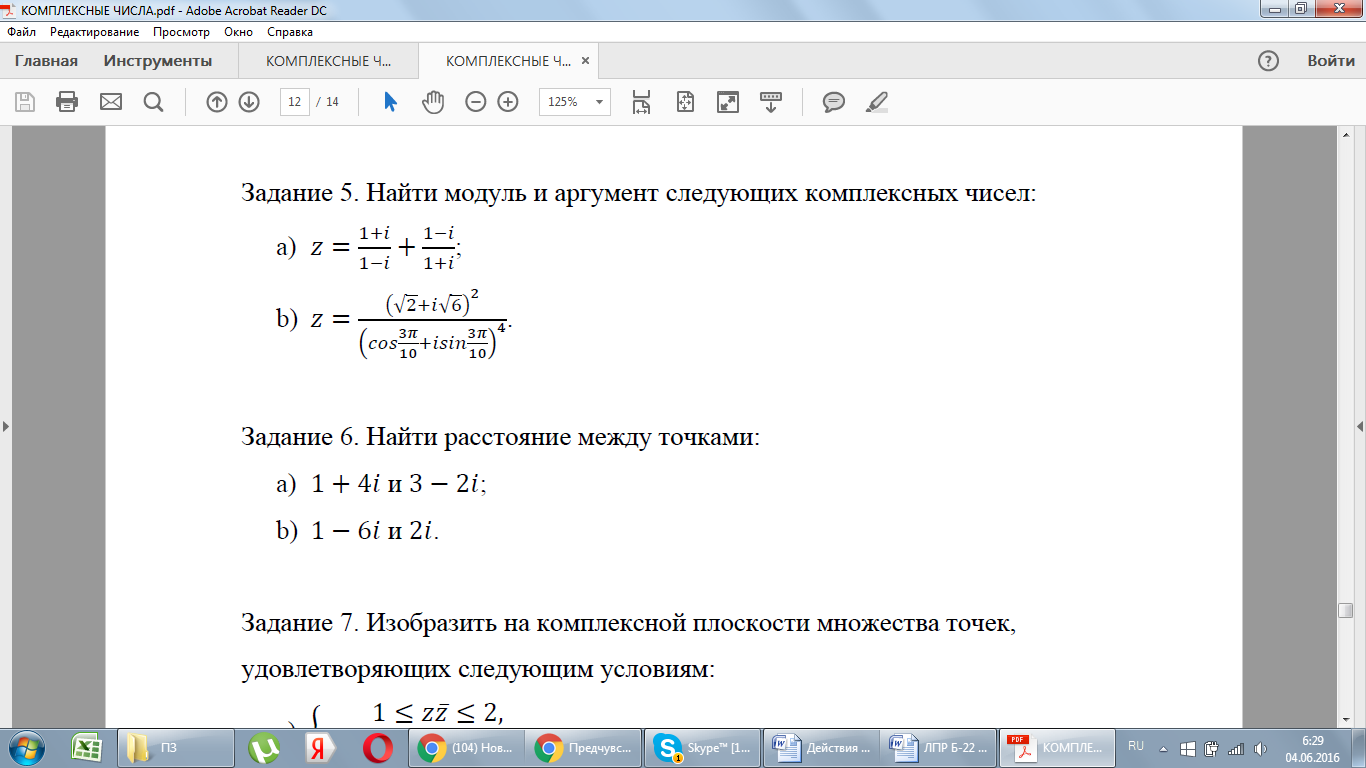
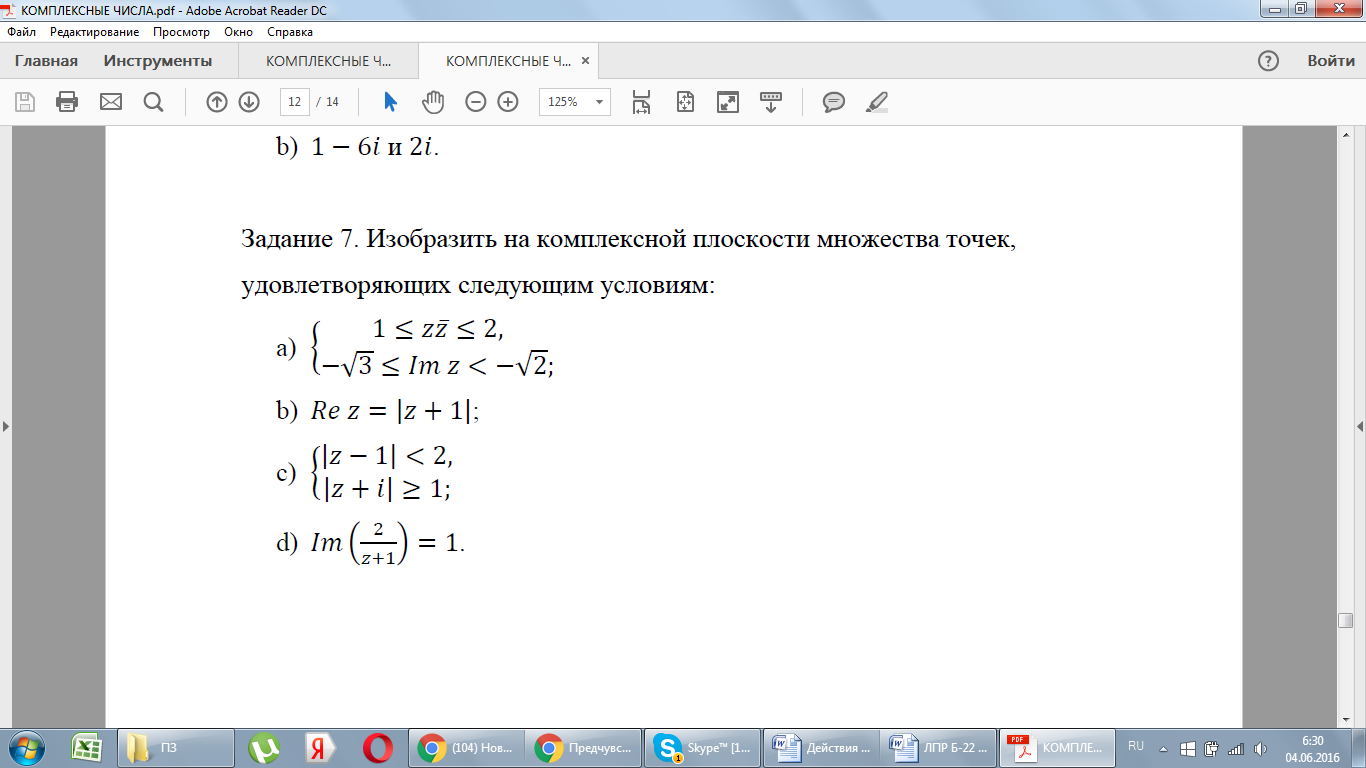
5. Первичная проверка и закрепление изученного материала (5 мин)

Метод проведения: Вопросы для закрепления изученного материала:

1. Какие числа называются комплексным?

2. Какие числа называются мнимой единицей?

3. По каким формулам мы складываем и вычитаем комплексные числа

6. Подведение итогов занятия (анализ и оценка успешности достижения

цели, результативность занятия) (5 мин)

Подведем итоги: поставленные цель и задачи урока выполнены.

7. Рефлексия (5 мин)

1. Что нового вы узнали?

2. Мы ответили на поставленный вопрос?

3. Что вы усвоили на уроке?

8.Задание на дом, инструктаж по его выполнению (5 мин).

Список литературы (для преподавателя):

1. Колмогоров, А.Н., Абрамов, А.М., Дудницын, Ю.П. и др. / Алгебра и начала математического анализа 10 - 111 кл.: учеб. для общеобраз. организаций с прил.на электрон. носителе/ под ред. А.Н. Колмогорова.- 22 - е изд. - М.: Просвещение 2013. - 384с.

2. Башмаков, М.И. математика: учебник для учреждения нач. и сред. проф. Образования / М.И. Башмаков. - 3-е изд., стер. - М.: Издательский центр «Академия», 2011. - 256 с.