Конспект к уроку 'Объём призмы' (11 класс)

Тема урока: Обьем призмы

Цель урока:

• обучить решению задач на вычисление объема призм, обобщить и систематизировать имеющиеся у учащихся сведения

• развивать логическое мышление, умение самостоятельно работать, навыки взаимоконтроля и самоконтроля, умение говорить и слушать;

• выработать привычку к постоянной занятости, каким - либо полезным делом, воспитание отзывчивости, трудолюбия, аккуратности.

Тип урока: урок изучения нового материала

Вид урока: работа в группах

Оборудование: карточки контроля, интерактивная доска, презентация,

семантическая карта, макеты призм.

Организация урока:

1. Организационный момент. Цель: формирование мотива, желание работать на уроке.

2. Проверка домашнего задания

3. Подготовка учащихся к усвоению материала.Цель: повторение необходимых теоретических сведений по теме, развитие умений говорить и слушать.

4. Изучение нового материала.Обьем призмы.

5. Первичная проверка усвоения знаний

6. Первичное закрепление знаний

7. Контроль и самопроверка знаний

8. Подведение итогов урока

9. Информация о домашнем задании

Ход урока

І. Организационный момент.

ІІ.Проверка домашнего задания. Задачи № 11, 12.Использовать ранее заготовленный флипчарт.

ІІІ. Подготовка учащихся к усвоению материала.Теоретическая разминка.

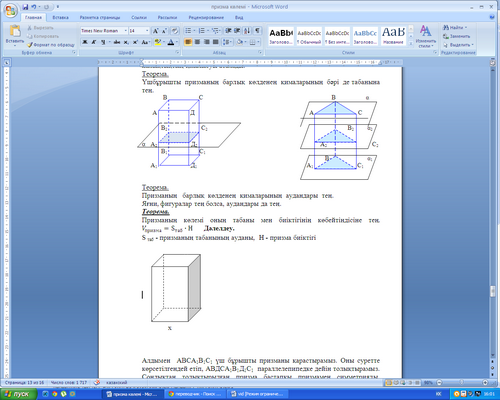
С помощью рисунка 1, 2, 3, 4 назовите:

• Боковые ребра призмы (рис 1).

• Боковую поверхность призмы (рис 1, рис 4).

• Высоту призмы (рис 2, рис 3).

• Прямую призму (рис 1,2,3).

• Наклонную призму (рис 4).

• Правильную призму (рис 1, рис 2).

• Диагональное сечение призмы (рис 1).

• Диагональ призмы (рис 1).

• Перпендикулярное сечение призмы (рис 2).

• Площадь боковой поверхности призмы.

• Площадь полной поверхности призмы.

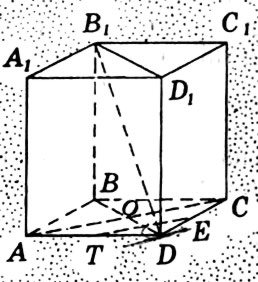
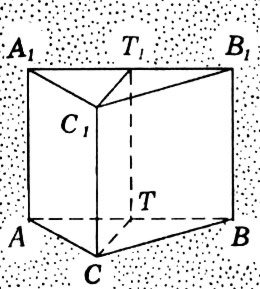
рис 1 рис 2

рис 3 рис 4

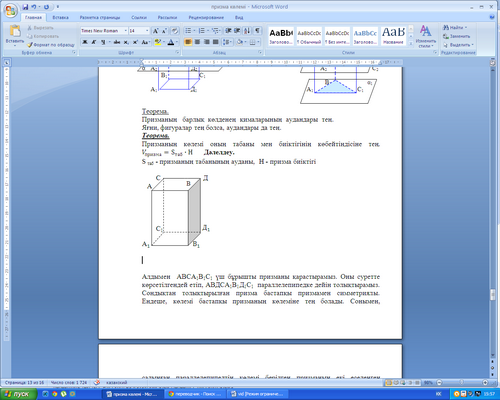
ІV. Изучение нового материала.Обьем призмы.

Объем призмы ранен V = S_основ • H. где S_основ - площадь основания призмы. H - ее высота.

Исходим из известного факта: объем параллелепипеда, равен

V_пар = S_основ • H

(S_основ - площадь основания, H - высота).

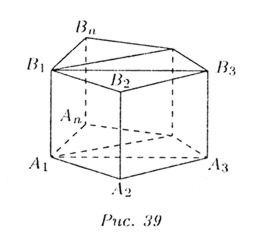
Начнем с частного случая. Пусть нам дана треугольная призма.

Достроим ее до параллелепипеда. Следовательно, параллелепипед состоит из двух равных призм, поэтому

С другой стороны

а высота призмы и параллелепипеда общая. Из равенства

следует, что

Переходим теперь к общему случаю. Дана произвольная призма. В ее основании лежит многоугольник. Проведя в нем диагонали, исходящие, из одной вершины, разбиваем многоугольник на треугольники (рис. 39). Сечения, проведенные через эти диагонали и соответствующие боковые ребра призмы делят ее на определенное число n треугольных призм. Для призмы с номером k объем равен

V_k = S_k • H

где S_k - площадь ее основания, H - высота первоначальной призмы. Складывая объем треугольных призм, получаем объем первоначальной призмы:

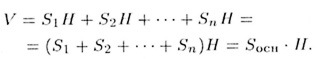
Формула установлена.

V. Первичная проверка усвоения знаний.

Найти обьем 4-х призм по макетам. Каждой группе разные призмы.

Физкультминутка.

VІ. Первичное закрепление знаний

Задача №16

Дано: равнобедренная трехсторонная наклонная призма

a = 4 дм

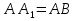В

Найти: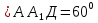

Решение : А С

В₁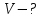

Е

Д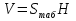

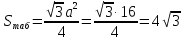А₁ С₁

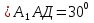
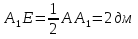
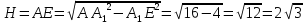
Ответ: 24 дм³

Задача №17

Дано : прямая призма

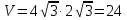
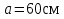
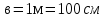
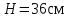
Найти: х-?

Решение: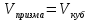

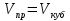
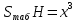
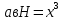
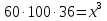
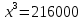
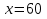
Ответ: 6 дм

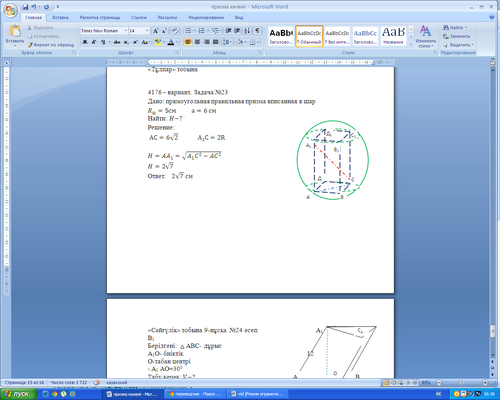
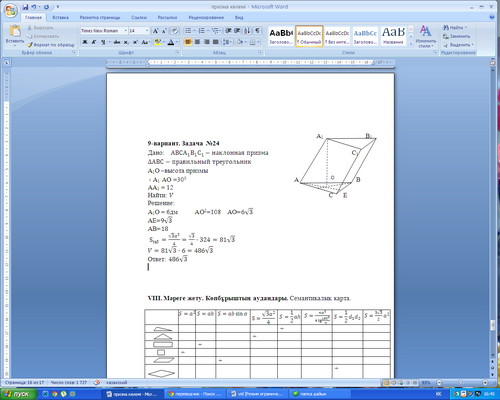
Решение задач на ЕНТ. Учитель у доски работает с "сильными" учащимися над решением следующих задач. Задачи комментируются в сопровождении слайдов

VІІ.Контроль и самопроверка знаний.Семантическая карта.

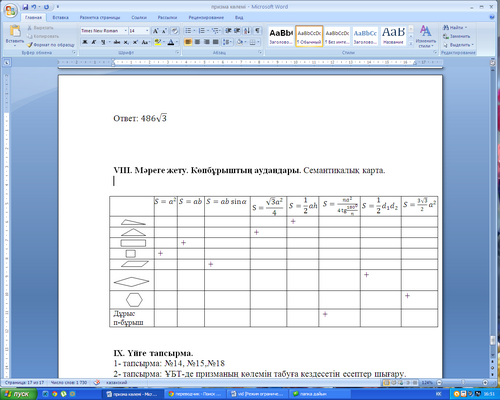
IХ. Домашнее задание. Задачи №14, №15,№18. Решение задач ЕНТ
Х.Подведение итогов.