Урок по предмету черчение

Тема: «Геометрические построения. Деление окружности». 9 класс

Автор: Шмаглиенко Наталия Николаевна, учитель ИЗО и черчения, ГУ СОШ № 10, г. Семей

1. Тип урока: комбинированный.

2. Оборудование: чертежные инструменты, тетрадь, учебник, мультимедиа.

3. Цели и задачи:

Цель: Ознакомить учащихся с темой «Геометрические построения. Деление окружности».

Задачи:

1 РАЗВИВАЮЩАЯ: развитие творческого мышления.

2 ВОСПИТАТЕЛЬНАЯ: формирование самостоятельности, аккуратности.

3 ОБРАЗОВАТЕЛЬНАЯ: научить детей геометрическим построениям: делению на равные части отрезков, окружности.

4. План урока:

1. Орг. момент.

2. Теоретическая часть.

3. Практическая часть.

4. Дом. задание.

5. Итог урока.

Ход урока:

Теоретическая часть:

При вычерчивание деталей, построение развёрток, приходится выполнять различные геометрические построения( строить углы, выполнять сопряжения, делить окружность на равные части). Многие элементы детали располагаются равномерно по окружности. Поэтому и возникает необходимость делить окружность на равные части.

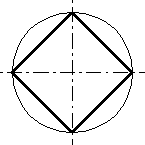
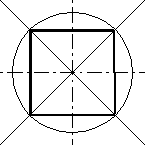
На 4 части:

Проводим 2 взаимно перпендикулярные прямые-осевые линии. Радиус возьмём 40мм.В первом случае мы воспользуемся тем, что поделив штрихпунктирными линиями окружность, мы уже получаем 4 точки окружности. Во втором случае, мы каждый сектор делим пополам : 90 разделить на 2 получаем 45 градусов. Можно воспользоваться линейками под углом 45 градусов.

1. 2.

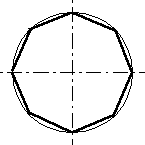
На 8 частей:

Совмещаем оба случая построения квадратов. Сперва делим окружность на 4 части, затем каждую часть делим пополам. Получаем 8 частей или восмигранник.

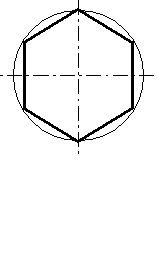
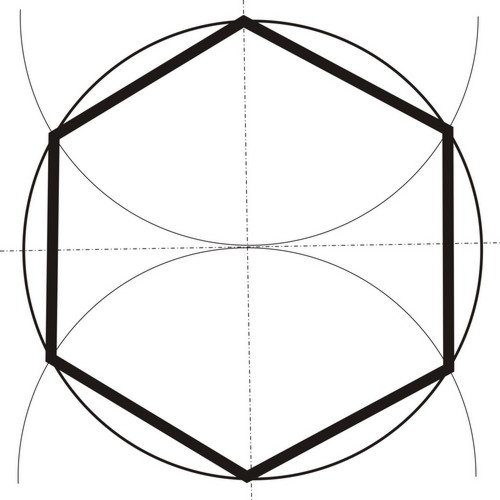
На 6 частей:

Раствор циркуля равен радиусу окружности, т.к. сторона 6-угольника равна описанной окружности. Из противоположных концов одного диаметра, описываем дуги(т.1 и т.4).

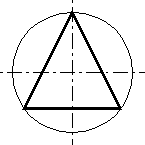
На 3 части:

Поставить циркуль на пересечении окружности с осевой. Описываем дугу равной радиусу окружности. Получаем 1 и 2 точки, 3 находим на противоположной стороне диаметра.

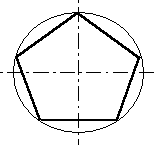
На 5 частей:

5 части окружности соответствует центральный угол в 72º(360º: 5=72º). При помощи транспортира находим нужный угол и откладываем этим же циркулем еще пять раз эту величину. Получаем пять частей. Можно вписать правильную звезду в окружность

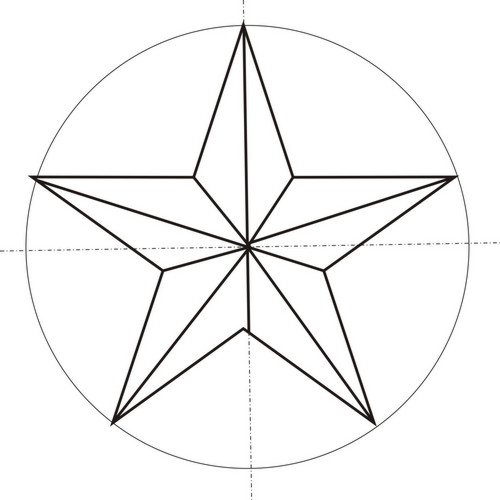
На 12 частей

Практическая часть:

Упражнение Выполнить окружность разделенную на 12 частей и вписанные в нее окружности.

Домашнее задание:

Выполнить сложный узор из деления окружности на равные части.