Задача на оптимизацию в EXCEL, 11 класс (из серии задач)

ЗАДАЧА №3

На упаковочной поточной линии работают четыре сотрудника. Операции упаковки последовательны. Время работы (в мин.) каждого сотрудника на каждой операции представлено в таблице. Необходимо наладить процесс упаковки так, чтобы сократить общее время упаковки (повысить производительность).

Операции

Сотрудники

А

В

С

D

1

9

8

8,5

7

2

8

8,8

8

8

3

8,5

7,5

7

7,4

4

8,8

8

7

7

РЕШЕНИЕ

Математическая модель задачи.

Исходные параметры модели задачи о назначениях

1. n -количество сотрудников, m - количество операций

2. a_i = 1 - единичное количество ресурса A_i (i =1,n) (сотрудники)

3. b_j = 1 - единичное количество работы B_j (j =1,m)(операции)

4. c_ij - характеристика качества выполнения работы B_j с помощью ресурса А_i.

Искомые параметры

1. x_ij - факт назначения или неназначения сотрудника А_i на операцию B_j:

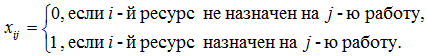
2. L(X) - общая (суммарная) характеристика качества распределения сотрудников по операциям.

Ограничения на переменные задачи.

Очевидно, что все переменные задачи неотрицательные и целые числа: x_ij ≥ 0 и x_ij - целые.

Кроме того, так как каждый сотрудник может выполнять только одну последовательность операций, должны удовлетворяться следующие ограничения:

другими словами в матрице (x_ij) суммы элементов по каждой строке и суммы элементов по каждому столбцу должны быть равны единицам. Это условие означает, что выбор претендентов должен быть таким, чтобы в матрице (x_ij), представляющей решение задачи, было бы по одной единице в каждой строке и по одной единице в каждом столбце, остальные элементы матрицы должны равняться нулю.

Целевая функция в задаче о назначениях.

Необходимо расставить сотрудников так, чтобы суммарное время упаковки было бы минимальным. Суммарное время вычисляется по формуле:

Окончательная математическая модель задачи записывается так:

при ограничениях:

Решение задачи в Excel.

Э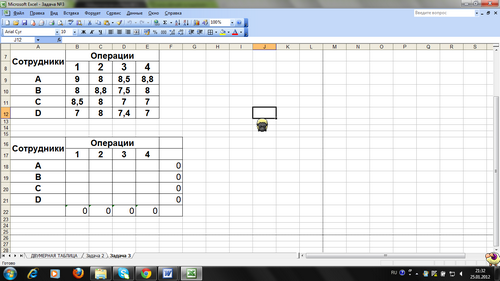кранные формы, задание переменных, целевой функции, ограничений и граничных условий задачи представлены на рис.1, 2, 2, и в табл.1

Рис.1

Формулы экранной формы задачи табл.1

Объект математической модели

Выражение в Excel

Переменные задачи

B18: E21

Формула в целевой ячейке I15

=СУММПРОИЗВ(В9:E12;В18:E21)

Ограничения по строкам в ячейках F18:F21

=СУММ(B18:E18) Копируем в диапазон F18:F21

Ограничения по столбцам

в ячейках B22:E22

=СУММ(В18:В21)

Копируем в диапазон B22:E22

Ограничения и граничные условия задачи

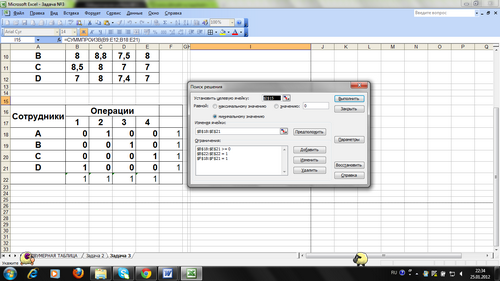
Рис.2

В окне «Параметры» установить«Линейная модель»

Результаты решения задачи:

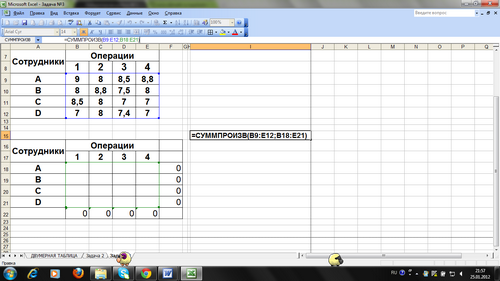
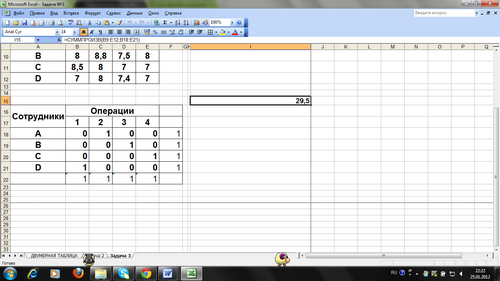
ВЫВОД.

Получили оптимальное распределение. Таким образом, чтобы сократить общее время упаковки (повысить производительность) надо:

Первую операцию выполняет сотрудник D,

Вторую операцию выполняет сотрудник А;

Третью операцию выполняет сотрудник В;

Четвертую операцию выполняет сотрудник С.