Разработка урока информатики в 9 классе по теме 'Системы счисления'

План-конспект урока

Тема урока: Системы счисления. Двоичная система счисления.

Цели урока:

1. Ввести понятие «Система счисления (СС)». Научиться переводить целые числа из десятичной СС в двоичную СС и обратно.

2. Развить логическое мышление.

3. Воспитать уверенность в своих силах.

Задачи урока:

1. Активизация и развитие познавательных процессов учащихся (восприятия, внимания, памяти, наблюдательности, сообразительности и т.д.);

2. Изучение нового материала;

3. Развитие логического мышления;

4. Создание деятельной, творческой обстановки в процессе урока, благотворно влияющей на эмоциональность, психику учащихся;

5. Внедрение компьютерных технологий в процесс обучения.

Оборудование: компьютер, проектор.

Ход урока

1. Организационный момент урока (2мин)

Сообщение темы (Слайд 1), целей (Слайд 2) и задач (Слайд 3) урока.

2. Объяснение нового материала.(25 мин)

- Скажите мне, пожалуйста, для чего нам нужны числа?

- Действительно, для записи информации о количестве объектов используют числа. Давайте посмотрим числа арабские, к которым мы привыкли и которыми пользуемся каждый день и числа римские. Они отличаются? Чем?

- Правильно, записываются по-разному.

Итак, числа записываются с использованием особых знаковых систем, которые называются системами счисления.

Давайте запишем определение систем счисления (Слайд 4).

Система счисления - это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами.

Все системы счисления делятся на две большие группы: позиционные и непозиционные системы счисления. (Слайд 5) (Зарисовать в тетрадь схему)

В позиционных СС количественное значение цифры зависит от ее положения в числе. (Записать в тетрадь)

- Как вы думаете, а в непозиционных? (слайд 5) (Записать в тетрадь)

Рассмотрим вначале позиционные СС, например десятичную СС. Число 579. Цифра 5 обозначает пять сотен, 7 - семь десятков, 9 - девять единиц.

Если поменять местами цифры, например, 5 и 7, то цифра 5 - станет обозначать пять десятков, 7 - семь сотен. (Записать пример в тетрадь)

- Одним из примеров непозиционных СС является римская СС (римские числа). Давайте подробнее рассмотрим, по какому принципу образуются числа в римской СС.

В римской СС числа получаются путем прибавления или вычитания. Например, число IX (9) получается путем вычитания единицы из десяти. Теперь переставим единицу слева направо, получили число XI (11) путем прибавления единицы к десяти. Таким образом, дописывая цифру справа от числа, прибавляем её, дописывая цифру слева от числа, отнимаем её. При этом количественное значение цифры от её положения в числе не изменяется. (Записать в тетрадь с слайда пример)

Запишем примеры позиционных и непозиционных СС. (Слайд 6) (Продолжить схему, которую начали на слайде 5 в тетради)

Обратите внимание, что в позиционных СС основание системы равно количеству цифр (знаков в её алфавите) и определяет во сколько раз различаются значения одинаковых цифр, стоящих в соседних позициях.

Вся информация в компьютере представлена в виде двоичного кода. Компьютер переводит информацию (числовую, текстовую, графическую, звуковую, видео) в последовательность нулей и единиц. Давайте посмотрим, как можно перевести числа из привычной нам десятичной СС в двоичную СС.

Для начала рассмотрим перевод целых чисел из десятичной СС в двоичную (слайд 7).

Алгоритм перевода:

1. Последовательно выполнять деление исходного целого десятичного числа и получаемых целых частных на основание системы (на 2) до тех пор, пока не получится частное, меньшее делителя, то есть меньшее 2.

2. Записать полученные остатки в обратной последовательности.

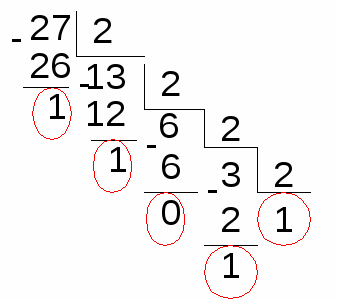
Теперь рассмотрим обратную задачу - перевод чисел из двоичной СС в десятичную. (Слайд 8)

Алгоритм перевода:

1. Двоичное число записать в развернутой форме.

Давайте вернемся в курс математики и вспомним, как записывается число в развернутой форме. (Пройти по гиперссылке «развернутой форме»).

Запишем число 579 в десятичной СС в развернутой форме.

Мы уже с вами выяснили, что в э том числе цифра 5 означает 5 сотен, 7 - семь десятков, 9 - девять единиц. Число 579 записано в привычной для нас свернутой форме. Мы настолько привыкли к такой форме записи, что уже не замечаем, как в уме умножаем цифры числа на различные степени числа 10.

В развернутой форме записи числа такое умножение записывается в явной форме (Слайд 11).

Аналогично, и для двоичной СС. В двоичной СС основание равно 2, а алфавит состоит из двух цифр (0 и 1). Следовательно, числа в двоичной системе в развернутой форме записываются в виде суммы степеней основания 2 с коэффициентами, в качестве которых выступают цифры 0 или 1 (Слайд 11).

Итак, вернемся к нашему примеру (через гиперссылку «назад») запишем число 11101001 в развернутой форме. (слайд 8)

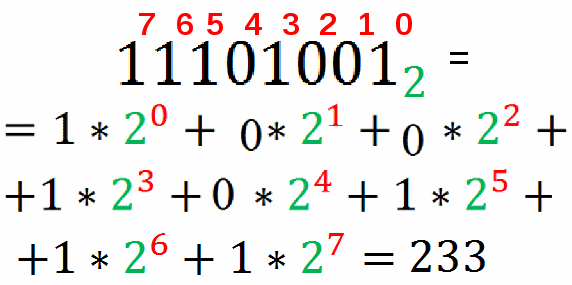
2. Произвести вычисления.

(Слайд 8)

- Теперь вы умеете переводить числа десятичной СС в двоичную СС и обратно. Давайте решим два примера на закрепление ваших знаний.

3. Закрепление нового материала (3 мин)

Примеры для самостоятельного решения и закрепления изученного материала. Перевести из десятичной СС в двоичную число. (Слайд 9)

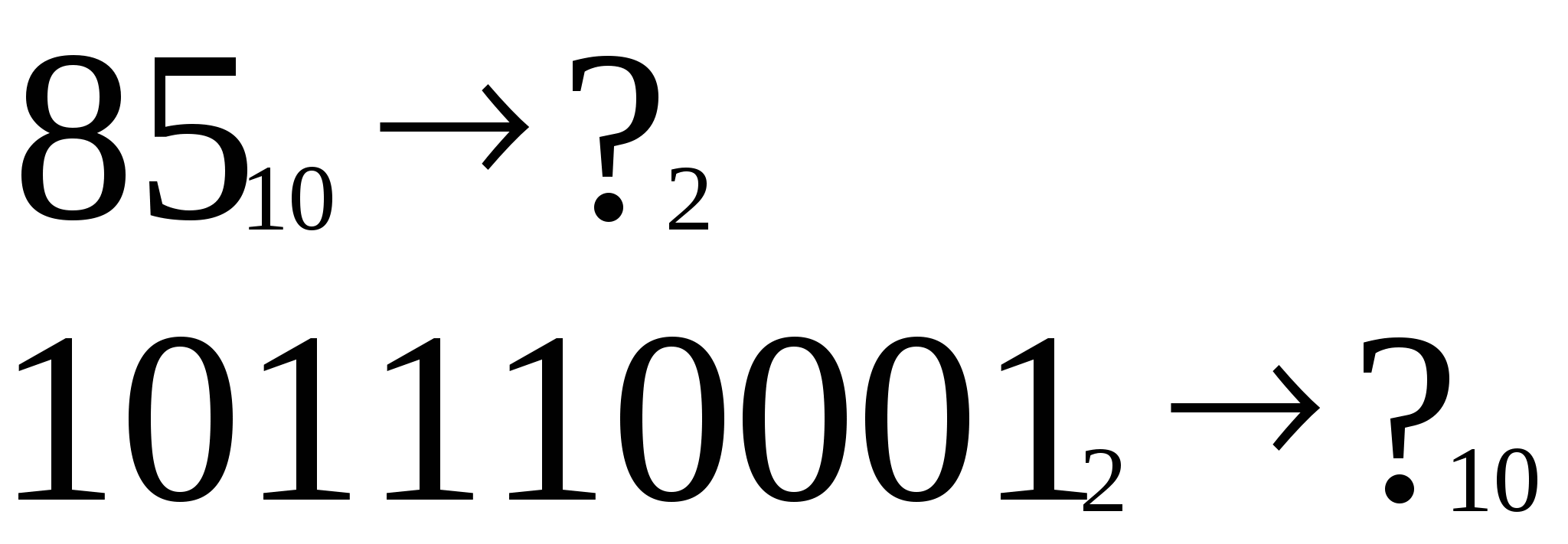
- Решили? Теперь проверьте себя.

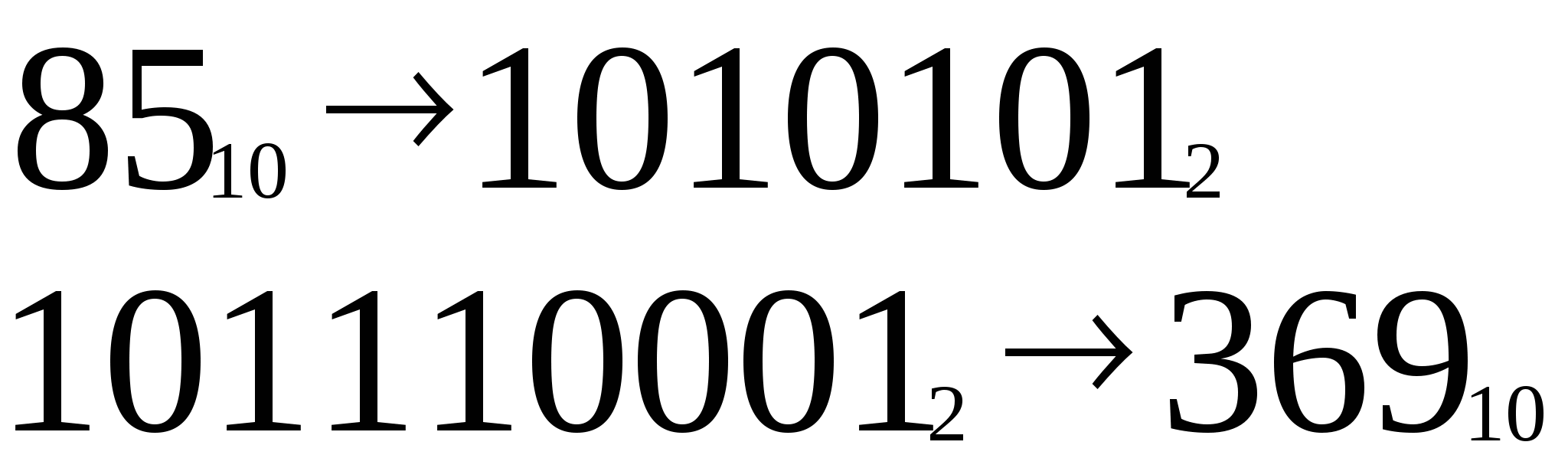
4. Самостоятельная работа (7 мин)

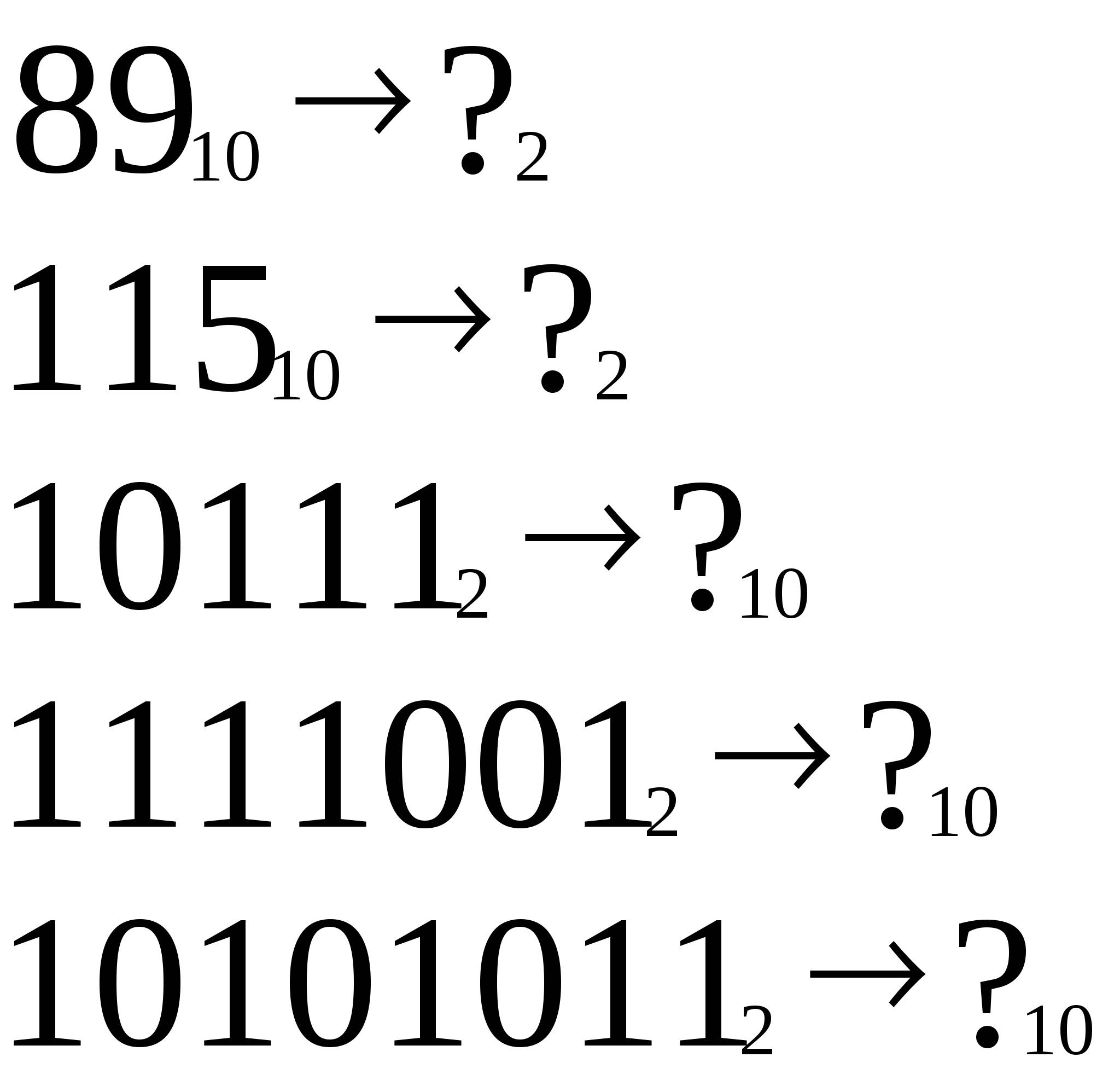
5. Подведение итогов урока. (5мин)

- Сегодня на уроке мы с вами провели большую работу и узнали много нового. Что для вас было новым? Что вы узнали?

Узнали, что числа записываются с использованием особых знаковых систем, которые называются системами счисления.

Все системы счисления делятся на две большие группы. Какие? (Позиционные и непозиционные).

Научились переводить числа из десятичной СС в двоичную и обратно.

4. Домашняя работа (Слайд 10). (3 мин)

- Открываем дневники, записываем домашнее задание: §17, № 6, №7,

§18, выучить конспект, дорешать примеры в тетради.

- В тетрадь запишите примеры.

- Урок окончен. До свидания.