- Учителю
- Способ решения систем логических уравнений
Способ решения систем логических уравнений
Решение систем логических уравнений табличным способами преобразованием логических выражений.
Данная методика основана на использование таблиц истинности, рассчитана на учащихся, которые владеют методами преобразования логических выражений. Если учащиеся плохо владеют этими методами, можно использовать и без преобразований. (Мы будем использовать преобразования). Для овладения этим способом решения, необходимы в обязательном порядке знание свойств основных логических операций: конъюнкции, дизъюнкции, инверсии, импликации и эквивалентности.
Алгоритм решения систем уравнений по этому методу:
-
Преобразовать логическое уравнение, упростить его.
-
Определить последовательность решения уравнений в системе, так как в большинстве случаев идет последовательное решение уравнений сверху вниз (как они расположены в системе), но есть варианты, когда удобнее, проще начать решать снизу вверх.
-
Построить таблицу переменных, где задать начальные значения первой переменной (или последней).
-
Последовательно прописать возможные варианты следующей переменной при каждом значении первой.
-
После решения предыдущего уравнения, переходя на следующее, обязательно обращать внимание: какие переменные используются в предыдущем и последующем уравнении, так как полученные при решении в предыдущих уравнениях значения переменных переходят как варианты для следующих уравнений.
-
Обращать внимание на получаемые количества решения при переходе к следующей переменной, т.к. может быть выявлена закономерность в увеличении решений.
Пример1.
¬X1 ˅ X2=1
¬X2 ˅ X3=1
¬X3 ˅ X4=1
….
¬X9 ˅ X10=1
Начнем с Х1 и посмотрим какие значения эта переменная может принимать: 0 и 1.
Затем рассмотрим каждое из этих значений и посмотрим, какое может быть при этом Х2.
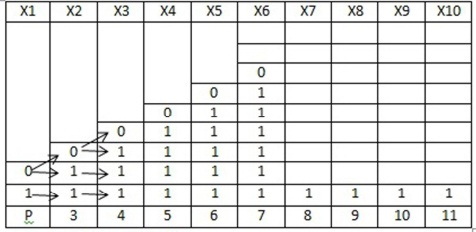
Ответ: 11 решений
Пример 2.
(X1˄ X2)˅(¬X1˄¬X2)˅(X1↔X3)=1
(X2˄ X3)˅(¬X2˄¬X3)˅(X2↔X4)=1
…
(X8˄ X9)˅(¬X8˄¬X9)˅(X8↔X10)=0
Преобразуем по формуле (A˄ B)˅ (¬A ˄ ¬B)= A↔B
Получаем:
(X1↔X2) ˅ (X1↔ X3) =1
(X2↔X3) ˅ (X2↔ X4) =1
…
(X8↔X9) ˅ (X8↔ X10) =0
Возьмем Х1=0 и посмотрим какие значение может принимать Х2. Теперь для каждого Х2 рассмотрим какие значения может принимать Х3 и т.д.
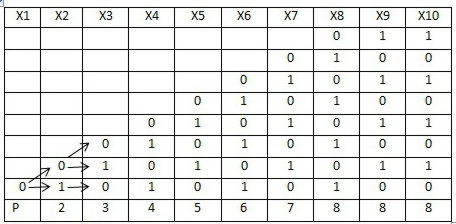
Для Х1 =0 - 8 решений
Возьмем Х1=1 и посмотрим какие значение может принимать Х2. Теперь для каждого Х2 рассмотрим какие значения может принимать Х3 и т.д.
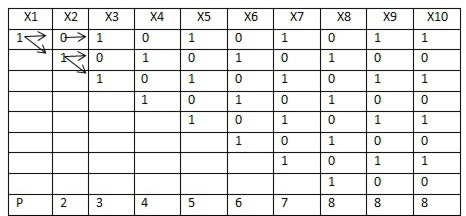
Для Х1=1 - 8 решений
Итого 8+8=16 решений
Ответ. 16 решений
Пример 3.
¬ (X1↔X2) ˄ (X1 ˅ X3) ˄ (¬X1 ˅ ¬X3)=0
¬ (X2↔X3) ˄ (X2 ˅ X4) ˄ (¬X2 ˅ ¬X4)=0
….
¬ (X8↔X9) ˄ (X8 ˅ X10) ˄ (¬X8 ˅ ¬X10)=0
После преобразований (A˅ B) ˄(¬A ˅¬B)= ¬(A ↔B)
получаем:
¬ (X1↔X2) ˄ ¬ (X1↔ X3)=0
¬ (X2↔X3) ˄ ¬ (X2↔ X4)=0
…..
¬ (X8↔X9) ˄ ¬ (X8↔ X10)=0
Возьмем Х1=0 и посмотрим какие значение может принимать Х2. Теперь для каждого Х2 рассмотрим какие значения может принимать Х3 и т.д
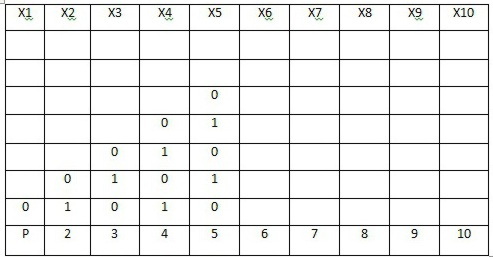
Получилось 10 решений для Х1=0
То же самое проделаем для Х1=1. Получим тоже 10 решений
Итого:10+10=20
Ответ: 20 решений.
Пример 4.
(Х1 ˄ Х2) ˅ (¬Х1 ˄ ¬Х2) ˅ (Х2 ˄ Х3) ˅ (¬Х2 ˄¬ Х3)=1
(Х2 ˄ Х3) ˅ (¬Х2 ˄ ¬Х3) ˅ (Х3˄ Х4) ˅ (¬Х3 ˄¬ Х4)=1
….
(Х8 ˄ Х9) ˅ (¬Х8˄ ¬Х9) ˅ (Х9 ˄ Х10) ˅ (¬Х9 ˄¬ Х10)=0
Преобразуем по формулам. (A˄ B)˅ (¬A ˄ ¬B)= A↔B. Получим:
(Х1↔ Х2) ˅ (Х2↔ Х3)=1
(Х2↔ Х3) ˅ (Х3↔ Х4)=1
(Х3↔ Х4) ˅ (Х4↔ Х5)=1
(Х4↔ Х5) ˅ (Х5↔ Х6)=1
(Х5↔ Х6) ˅ (Х6↔ Х7)=1
(Х6↔ Х7) ˅ (Х7↔ Х8)=1
(Х7↔ Х8) ˅ (Х8↔ Х9)=1
(Х8↔ Х9) ˅ (Х9↔ Х10)=0
Начнем с конца, потому что в последнем уравнении переменные определятся однозначно.
Пусть Х10=0, тогда Х9=1, Х8=0, Х7=0, Х6=0, а следующие переменные могут принимать разные значения. Будем рассматривать каждое.

Видим некоторую закономерность: Количество следующих решений равно сумме двух предыдущих.
Итого 21 решение для Х10=0
Теперь рассмотрим для Х10=1. Получаем тоже 21 решение
Итого:21+21=42
Ответ: 42 решения
Пример 5.
(X1 ˄ X2) ˅ (¬X1 ˄ ¬X2) ˅ (¬X3 ˄ X4) ˅ (X3 ˄ ¬X4)=1
(X3 ˄ X4) ˅ (¬X3 ˄ ¬X4) ˅ (¬X5 ˄ X6) ˅ (X5 ˄ ¬X6)=1
(X5 ˄ X6) ˅ (¬X5 ˄ ¬X6) ˅ (¬X7 ˄ X8) ˅ (X7 ˄ ¬X8)=1
(X7 ˄ X8) ˅ (¬X7 ˄ ¬X8) ˅ (¬X9 ˄ X10) ˅ (X9˄ ¬X10)=1
Преобразуем по формулам: (¬A ˄ B) ˅ (A ˄ ¬B)= A↔ ¬B
(A˄ B)˅ (¬A ˄ ¬B)= A↔B
(X1↔ X2) ˅ (X3 ↔ ¬X4)=1
(X3↔ X4) ˅ (X5 ↔ ¬X6)=1
(X5↔ X6) ˅ (X7 ↔ ¬X8)=1
(X7↔ X8) ˅ (X9 ↔ ¬X10)=1
Рассмотрим какие значения могут принимать Х1 и Х2: (0,0), (0,1), (1,0), (1,1).
Рассмотрим каждый вариант и посмотрим какие значения при этом могут принимать Х3, Х4
Начиная с Х7, Х8 будем сразу записывать количество решений, так как сразу видно, что когда значения одинаковые (1,1) и (0,0), то следующие переменные имеют 4 решения, а когда разные (0,1) и (1,0) - 2 решения.
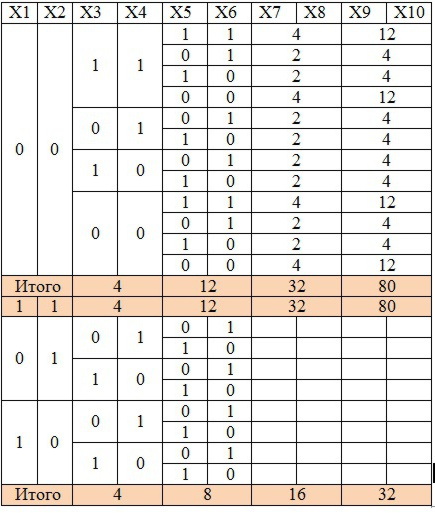
Итого: 80+80+32=192
Ответ:192 решения
Пример 6.
(Х1↔ Х2) ˅ (Х2 ↔Х3)=1
(Х2↔ Х3) ˅ (Х3↔Х4)=1
(Х3↔ Х4) ˅ (Х4 ↔Х5)=1
….
(Х8↔ Х9) ˅ (Х9 ↔Х10)=1
Возьмем Х1=0 и посмотрим какие значение может принимать Х2. Теперь для каждого Х2 рассмотрим какие значения может принимать Х3 и т.д.
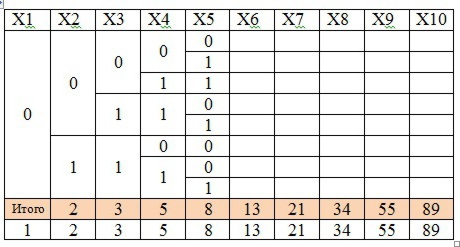
Видим некоторую закономерность: Количество следующих решений равно сумме двух предыдущих.
То же самое для Х1=1 получаем 89 решений
Итого: 89+89=178 решений
Ответ: 178 решений
Решим еще одним способом
(Х1↔ Х2) ˅ (Х2 ↔Х3)=1
(Х2↔ Х3) ˅ (Х3↔Х4)=1
(Х3↔ Х4) ˅ (Х4 ↔Х5)=1
….
(Х8↔ Х9) ˅ (Х9 ↔Х10)=1
Введем замену:
T1=(Х1↔ Х2)
T2=(Х2↔ Х3)
T3=(Х3↔ Х4)
T4=(Х4↔ Х5)
T5=(Х5↔ Х6)
T6=(Х6↔ Х7)
T7=(Х7↔ Х8)
T8=(Х8↔ Х9)
T9=(Х9↔ Х10)
Получаем:
T1 ˅ T2=1
T2 ˅ T3=1
T3 ˅ T4=1
T4 ˅ T5=1
T5 ˅ T6=1
T6 ˅ T7=1
T7 ˅ T8=1
T8 ˅ T9=1
T9 ˅ T10=1
Возьмем T1=1 и используем свойства дизъюнкции:
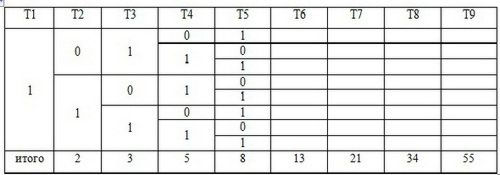
НО Вспомним, что
T1=(Х1↔ Х2)
T2=(Х2↔ Х3) и т.д.
Воспользуемся свойством эквивалентности и убедимся, глядя на таблицу, что
Когда Т =1, то получается два решения. А когда =0 -одно решение.
Следовательно, можно подсчитать количество единиц и умножить их на 2+ количество нулей. Подсчет, так же используя закономерность.
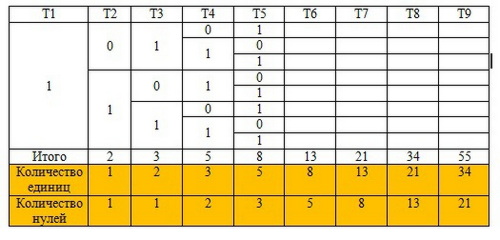
Получается, что количество единиц = предыдущему общему количеству решений Т, а количество нулей равно предыдущему количеству единиц
Итак. Получим. Так как единица дает два решения, то 34*2=68 решений из единицы+21 решение из 0.
Итого 89 решений для Т=1. Аналогичным способом получаем 89 решений для Т=0
Итого 89+89=178
Ответ: 178 решений
Пример 7.
(X1 ↔X2) ˅ (X3↔ X4) ˄ ¬(X1 ↔X2) ˅ ¬(X3↔ X4)=1
(X3 ↔X4) ˅ (X5↔ X6) ˄ ¬(X3 ↔X4) ˅ ¬(X5↔ X6)=1
(X5 ↔X6) ˅ (X7↔ X8) ˄ ¬(X5 ↔X6) ˅ ¬(X7↔ X8)=1
(X7 ↔X8) ˅ (X9↔ X10) ˄ ¬(X7 ↔X8) ˅ ¬(X9↔ X10)=1
Введем замену:
T1=(X1 ↔X2)
T2=(X3↔ X4)
T3=(X5↔ X6)
T4=(X7 ↔X8)
T5=(X9↔ X10)
Получим:
(Т1 ˅ Т2) ˄ ¬( Т1 ˅¬ Т2)=1
(Т2 ˅ Т3) ˄ ¬( Т2˅¬ Т3)=1
(Т3 ˅ Т4) ˄ ¬( Т3 ˅¬ Т4)=1
(Т4 ˅ Т5) ˄ ¬( Т4˅¬ Т5)=1
Рассмотрим какие могут быть Т:
-
Т1
Т2
Т3
Т4
Т5
Итого
0
1
0
1
0
32
1
0
1
0
1
32
ТK≠ТК+1 И ТK=ТК+2
Получаем: 25=32 для Т
Итого: 32+32=64
Ответ: 64 решения.