Статья на тему 'Игровые технологии'

Статья на тему "Игровые технологии"

Игровые технологии относятся к педагогическим технологиям, основанным на активизации и интенсификации деятельности учащихся. Игра - это вид деятельности в условиях ситуаций, направленных на воссоздание и усвоение общественного опыта, в котором складывается и совершенствуется самоуправление поведением. Использование игровых технологий является одним из способов достижения сознательного и активного участия обучаемых в самом процессе обучения.

Деловая игра, как бы сжимая время, сближает время, сближает события, далеко разнесенные в практике, и тем самым отчетливо показывают участникам возможности долгосрочных стратегий и их влияния на эффективность деятельности. Кроме того, игра обеспечивает максимальное эмоциональное вовлечение участников в события, допуская возможность вернуть ход и попробовать другую стратегию, создает оптимальные условия для развития предусмотрительности, гибкости мышления и целеустремленности. Она приучает к коллективным действиям, принятию как самостоятельных, так и скоординированных решений, повышает способность руководить и подчиняться, стимулирует практические навыки, развивает воображение и интуицию. При игре меняется мотивация обучения, знания усваиваются не про запас, не для будущего времени, а для обеспечения непосредственных игровых успехов обучающихся в реальном для них процессе. Помимо этого, достоинством деловых игр является радикальное сокращение времени накопления опыта. Опыт, который в обычных условиях накапливается в течение многих лет, может быть получен с помощью деловых игр в течение недели или месяца. Как правило, игры проводятся по периодам (циклам), которые имитируют период продолжительностью в день, неделю, квартал или год. Опыт, который в обычных условиях накапливается в течение недели или месяца. Как правило, игры проводятся по периодам (циклам), которые имитируют период продолжительностью в день, неделю или год.

Качество игры тем выше, чем ближе модель к изучаемому или исследуемому механизму. Наибольшей активности позволяют достичь компьютерные модели и компьютерные игровые технологии. Если деловая игра как имитационная модель действительно отражает основные закономерности изучаемых явлений, то она может с успехом применяться как в учебных, так и в исследовательских целях.

Тема урока: «Взаимное расположение двух окружностей».

Цели урока:

Обучающие:

1)рассмотреть различные случаи взаимного расположения двух окружностей; совершенствовать навыки решения задач.

Развивающие:

1) совершенствовать умения логически мыслить и выражать свои мысли вслух;

2) стимулировать познавательную деятельность учащихся постановкой проблемного задания, оценкой и поощрением;

Воспитательные:

1) воспитывать у учащихся стремление к совершенствованию своих знаний;

2) воспитывать интерес к предмету.

Ход урока.

1. Организационный момент.

2. Мотивация урока.

Как сказал древнегреческий философ Саади: "Ученик, который учится без желания - это птица без крыльев".

И мне бы хотелось, чтобы у вас было желание учиться, узнавать что-то новое, неопознанное не только на сегодняшнем уроке, а всегда и только в этом случае своими "крыльями" будете "взлетать" все выше и выше.

А также мне очень хочется обратиться к словам известного российского математика А.И. Мордковича: "Кто с детских лет занимается математикой, этот развивает внимание, тренирует свой мозг, свою волю, воспитывает в себе настойчивость и упорство в достижении цели".

− У каждого из вас на парте лежит «Дерево Блоба». Укажите где вы находитесь на нем.

3. Актуализация опорных знаний. Проверка д/з.

Найдите ошибку:

• Окружностью называется множество точек плоскости, равноудалённых от точки.

• Радиус - это отрезок. Радиус - это отрезок, соединяющий точку окружности с ее центром.

• Отрезок, соединяющий две точки, окружности называется диаметром. Хорда, проходящая через центр окружности, называется диаметром.

• Хорда - часть диаметра. Отрезок, соединяющий две точки окружности, называется хордой.

• Окружность называется описанной около треугольника, если она соединяет все его вершины. Окружность называется описанной около треугольника, если она проходит через все его вершины.

• Центр окружности, описанной около треугольника, является точкой пересечения медиан к стороне треугольника. Центр окружности, описанной около треугольника, является точкой пересечения серединных перпендикуляров сторон этого треугольника.

• Прямая, проходящая через точку окружности перпендикулярно к радиусу, проведённому в эту точку, называется касательной.

• Окружность называется вписанной в треугольник, если она касается всех его отрезков. Окружность называется вписанной в треугольник, если она касается всех его сторон.

• Центр окружности, вписанной в треугольник, является точкой пересечения его перпендикуляров.

4. Изучение нового материала.

Перейдем к анализу возможных случаев расположения двух окружностей

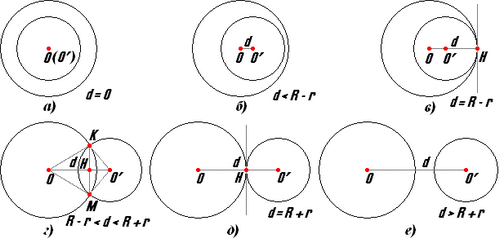
а) Центры окружностей совпадают. Такие окружности называются концентрическими.

В случае равенства радиусов они совпадают. Если же радиусы этих окружностей не равны, то одна из них лежит внутри другой. Образуется фигура, которую называют кольцом.

б) Пусть теперь центры окружностей различны. Соединим их прямой, она называется линией центров данной пары окружностей.

Взаимное расположение окружностей будет зависеть только от соотношения между величиной отрезка d, соединяющего их центры, и величинами радиусов окружностей R,r.

1. Расстояние между центрами меньше разности радиусов: d>R-r (рис б).

2. Расстояние между центрами равно разности радиусов: d=R-r (рис в). Малая окружность лежит внутри большой, но имеет с ней общую точку на линии центров. Говорят, что имеет место внутреннее касание, а такие окружности называют внутренне касающимися.

Определение 16. Внутренне касающимися называют окружности, имеющие одну общую точку, причем центр меньшей из них расположен внутри большей.

Точка касания внутренне касающихся окружностей лежит на линии центров.

3. Расстояние между центрами больше разности радиусов, но меньше их суммы: R-r

Пересекающимися называют окружности, имеющие две общие точки.

4. Расстояние между центрами равно сумме радиусов: d=R+r (рис д)

Внешне касающимися называют окружности, имеющие одну общую точку, причем центр одной из них расположен за пределами второй.

Точка касания внешне касающихся окружностей лежит на линии центров.

5. Расстояние между центрами больше суммы радиусов: d>R+r

5. Закрепление нового материала.

Решить № ...

6. Итоги урока. Д/з. Рефлексия.

Затем Принцип «Микрофон». (Ученики по очереди дают аргументированный ответ на один из вопросов).

Вопросы к зачету:

Вариант 1:

1. Окружность -…

2. Радиус окружности-…

3. Диаметр окружности -…

4. Построить прямую, пересекающую окружность.

5. Построить окружность и точку А на окружности. Провести касательную к окружности через точку А.

6. Привести примеры предметов, имеющих форму круга.

7. Построить две окружности, с внешним касанием.

8. Найдите расстояния между центрами этих окружностей.

9. Начертите произвольный треугольник и опишите около него окружность. Где расположен центр данной окружности?

Вариант 2:

1. Круг -…

2. Хорда окружности-…

3. Соотношение между радиусом и диаметром окружности.

4. Построить прямую, не пересекающую окружность.

5. Построить окружность и точку В на окружности. Провести касательную к окружности через точку В.

6. Привести примеры предметов, имеющих форму окружности.

7. Построить две окружности, с внутренним касанием.

8. Найдите расстояния между центрами этих окружностей.

9. Начертите произвольный треугольник и впишите в него окружность. Где расположен центр данной окружности?