Урок информатики 8 класс

Урок информатики в 8 классе

по теме "Системы счисления"

Цели урока:

1. знакомство с системами счисления, историей их создания, способами записи чисел в разных системах счисления, правилами перевода чисел из одной системы счисления в другую.

2. Формирование умений переводить числа из одной системы счисления в другую

3. Развитие алгоритмического, логического мышления познавательного интереса к предмету.

4. Воспитание коммуникативных качеств.

Планируемы результаты:

личностные:

• формирование ответственного отношения к учению на основе мотивации к обучению и познанию;

• формирование осознанного, уважительного и доброжелательного отношения к другому человеку, его мнению;

• формирование коммуникативной компетентности в общении и сотрудничестве со сверстниками и взрослыми в процессе учебной деятельности.

метапредметные:

• умение определять понятия, создавать обобщения, классифицировать, строить рассуждение, умозаключение и делать выводы;

• умение создавать, применять различные продукты для решения учебной задачи;

• умение оценивать правильность выполнения учебной задачи, собственные возможности её решения;

• развитие ИКТ-компетенции.

предметные:

• знать: историю развития систем счисления, определения: системы счисления, основание и алфавит системы счисления, применение систем счисления в жизни.

• уметь: переводить числа из десятичной системы счисления.

Оборудование:

• мультимедийный проектор;

• презентация «Системы счисления»;

• интерактивная доска;

• ПК, программа Калькулятор;

ХОД УРОКА

I. Организационный момент.

Учитель приветствует учащихся, проверяет готовность их к уроку, отмечает отсутствующих.

II. Актуализация изученных понятий.

Учитель задает вопросы:

1. Какие типы информации вам известны?

2. В каком виде представляется информация в компьютере?

3. Как представляется числовая информация в нашей жизни?

Дети отвечают на вопросы.

III. Проблемная ситуация.

Учитель: (читает стихотворение)

СКОЛЬКО ЛЕТ ДЕВОЧКЕ

(А. Стариков)

Ей было тысяча сто лет,

Она в сто первый класс ходила,

В портфеле по сто книг носила -

Все это правда, а не бред.

Когда, пыля десятком ног,

Она шагала по дороге,

За ней всегда бежал щенок

С одним хвостом, зато стоногий.

Она ловила каждый звук

Своими десятью ушами,

И десять загорелых рук

Портфель и поводок держали.

И десять темно-синих глаз

Рассматривали мир привычно,

Но станет все совсем обычным,

Когда поймете наш рассказ

Учитель: Возможно ли это? И если да, объясните, почему.

Учащиеся отвечают на вопрос, предлагают гипотезы.

Учитель: Как вы думаете, чем мы займемся на сегодняшнем уроке?

Учащиеся формулируют цель урока.

Учитель: Разобраться в невероятностях стихотворения вы сможете в конце нашего сегодняшнего путешествия по истории чисел, которое мы с вами совершим.

В путь!

IV. Изучение нового материала (с использованием мультимедийной презентации) .

Учитель: Пифагорийцы говорили: "Всё есть число", как вы думаете, почему? Согласны ли вы с этим лозунгом?

Учащиеся отвечают на вопросы.

Учитель: Современного человека повсюду окружают числа: номера телефонов, машин, паспорта, стоимость товаров, покупки. Потребность в счете у людей появилась очень давно. Даже первобытному человеку приходилось считать, например, количество собранных фруктов или пойманной рыбы. Счет необходим был и при обмене.

Числа изображаются с помощью различных знаков - цифр. Определенный набор знаков составляют систему счисления.

Система счисления - совокупность приемов и правил записи чисел с помощью определенного набора символов.

На протяжении многовековой истории человечества существовало много различных систем счисления, некоторые дошли и до наших времен, а некоторые остались в истории и одна из них - единичная система счисления. Вспомните, как отвечает на вопрос о возрасте маленький ребенок (учащиеся отвечают - на пальцах). А как вы учились считать в 1 классе? (учащиеся отвечают - с помощью счетных палочек). Так же учились считать и наши предки.

На раскопках стоянок древних людей археологи находят изображения в виде засечек, черточек на твердых поверхностях: камне, глине, дереве - это так считали наши предки какие-то предметы, мешки, скот. Но записывать большие числа с помощью такой системы счисления неудобно, не так ли? И поэтому их начали группировать по 3, 5, 10 палочек. Так возникли более удобные системы счисления.

Из таких цифр строили свои числа древние египтяне. В такой записи чисел каждая цифра повторялась не более 9 раз, в противном случае эта запись заменялась одним вышестоящим числом

Попробуйте узнать и прочитать это число?

Ученик: 2521

Учитель: А эти символы вам известны? (на слайде римские цифры). Где вы их встречали?

Учащиеся отвечают: В оглавлениях, в обозначении столетий, в размерах одежды.

Учитель: Да, это римская система счисления. Числа в ней строятся по определенным правилам из латинских букв, каждая из которых задаёт определенное число.

Попробуйте отгадать: что это за число CDXXIV?

Ученик: 424

Учитель: У наших древних предков тоже была своя - древнерусская алфавитная система счисления. В качестве цифр наши предки использовали 27 букв кириллицы, только над ними для отличия ставили специальный знак - ТИТЛО.

А число 10000 обозначалось той же буквой, что и 1, только без титло, её обводили кружком и число называли "ТЬМОЙ".

Самая большая из величин называлась "КОЛОДА" и она равнялась 10⁵⁰, считалось, что "БОЛЕЕ СЕГО НЕСТЬ ЧЕЛОВЕЧЕСКОМУ УМУ РАЗУМЕВАТИ".

Учитель: Зависит ли от положения символа(цифры) в древнеегипетской, единичной, римской системах счисления ее значение?

Учащиеся - нет

Учитель: Действительно, все их можно объединить по одному признаку: позиция цифры в записи числа не влияет на её значение. Они получили название непозиционные системы счисления.

Учитель: А как обстоит дело с арабскими цифрами, которые мы используем в жизни и на уроках математики.

Учащиеся отвечают

Учитель: Вместе с непозиционными существуют и позиционные системы счисления. В них количественное значение каждой цифры числа зависит от того, в каком месте (позиции или разряде) записана та или иная цифра.

Примером позиционной системы счисления является вавилонская система счисления - шестидесятеричная. Кстати, мы с вами тоже ее используем. Вспомните, где?

Ученик: При измерении времени, углов.

В XIX веке довольно широкое распространение получила двенадцатеричная система счисления. Например, на Руси счет велся дюжинами. Английский фунт тоже равен 12 шиллингам. А где мы сегодня встречаемся с двенадцатеричной системой счисления?

Ученик: Год - 12 месяцев, половина суток - 12 часов, сервизы и столовые приборы рассчитаны на 12 персон.

Десятичная система счисления появилась в Индии в \/ в.н.э. и возникла она после появления цифры 0, которую придумали греческие астрономы для обозначения отсутствующей величины. Впоследствии с этой системой счисления познакомились арабы. Они по достоинству оценили её, начали использовать и в ХII веке завезли в Европу. И с этого времени человечество пользуется этой системой счисления. Цифры 10-ной СС называются арабскими, хотя начало они получили в Индии.

С появлением информатики, вычислительной техники нашла свое применение двоичная система счисления, корни которой уходят в древний Китай. Система гадания китайской Книги перемен при внимательном анализе обнаруживает в своей основе двоичную систему счисления и позиционный принцип записи чисел.

А почему её используют в информатике?

Учащиеся пытаются ответить на вопрос.

Потому что компьютер - это электронное устройство. Электрическая цепь может быть только в двух состояниях - замкнута или разомкнута, сигнал может либо проходить, либо нет, участок диска может быть намагничен или не намагничен. Это удобно отражать с помощью всего лишь двух цифр - 1 и 0.

В настоящее время наиболее распространены десятичная, двоичная, восьмеричная и шестнадцатеричная системы счисления.

Количество различных символов, используемых для изображения числа в позиционных системах счисления, называется основанием системы счисления. А множество всех символов, используемых для записи чисел в данной системе счисления - ее алфавитом.

Любое число можно представить в виде суммы произведений значащих цифр числа на степени основания СС. Такое представление называется развернутой формой записи числа.

155255₁₀ = 1 ·10⁵ + 5 ·10⁴ + 5 ·10³ + 2 ·10² + 5 ·10¹ + 5 ·10⁰

На этом принципе основан перевод чисел из любой СС в десятичную СС. Так, для перевода двоичного числа в десятичное нужно записать его в развернутой форме

111101₂ = 1 ·2⁵ + 1 ·2⁴ + 1 ·2³ + 1 ·2² + 0 ·2¹ + 1 ·2⁰ = 32 + 16 + 8 + 4 + 1 = 61₁₀

II. Перевод в десятичную СС

Для обратного перевода десятичного числа в двоичное необходимо делить данное число на 2, фиксируя остатки. Деление продолжается до тех пор, пока частное не станет меньше делителя (основания системы). Остатки записываются в обратном порядке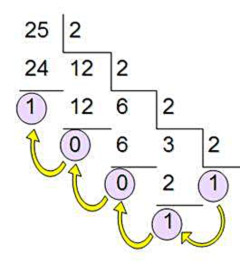

Пример: перевести число 25₁₀ из десятичной в двоичную:

25₁₀ = 11001₂

V. Закрепление изученного материала.

Практическая работа Перевод чисел из одной системы счисления в другую

(учащиеся работают в тетрадях и отмечают в листах самоконтроля оценку своих действий в соответствии с критериями)

1. Перевести число 849 с помощью электронного Калькулятора в двоичную, восьмеричную, шестнадцатеричную системы счисления

2. Самостоятельная работа.Поставьте вместо знака ? знак <, > или =.

• 285₁₀ ? 11D₁₆ (Ответ: 285₁₀ = 285₁₀ )

• 111111₂ ? 1111₈ (Ответ: 63₁₀ < 585₁₀ )

• 6С₁₆ ? 101001₂ (Ответ: 108₁₀ > 41₁₀ )

• 55₁₆ ? 125₈ (Ответ: 85₁₀ = 85₁₀ )
  
  После выполнения задания ответы демонстрируются на экране. Учащиеся проверяют свои результаты.

3. Ну а теперь давайте вернемся к задаче и вопросам, поставленным в начале урока.

Учитель: Сколько же лет девочке? В какой класс она ходила? Сколько книг в портфеле?

Ученики: 12 лет, 5 класс, 4 книги.

Дополнительные задания

1. Переведи в десятичную систему счисления: 345, 110011,012, 1ВС16

2. Расположите числа, записанные в различных системах счисления, в порядке возрастания:

• 35₁₀, 36₈, 3А₁₆, 100101₂, 130₄ (Ответ: 130₄ , 36₈, 35₁₀, 100101₂, 3А₁₆)

• 111001₂, 64₈, 9Е₁₆, 25₁₀, 210₃ (Ответ: 210₃, 25₁₀, 64₈, 111001₂, 9Е₁₆)

• 72₈, 156₁₀, 101001₂, 8В₁₆, 232₅ (Ответ: 101001₂, 72₈, 2325, 8В₁₆, 156₁₀)

• 12D₁₆, 78₈, 100011₂, 541₁₀, 124₅ (Ответ: 100011₂, 124₅, 788, 12D₁₆, 541₁₀)

Учащиеся выполняют задания в группах за компьютером, используя программу «Инженерный калькулятор».

VI. Рефлексия.

Учитель задает вопросы:

1. С чем вы познакомились на сегодняшнем уроке?

2. Что нового вы узнали о числах?

3. Какие трудности вы испытывали при переводе чисел из одной системы счисления в другую?

4. Где можно применить новые знания?

Учащиеся отвечают на вопросы, оценивают свою работу на уроке, записывают домашнее задание.

Список использованной литературы

1. Семакин И.Г. Информатика. Базовый курс. 7-9 кл М.: БИНОМ. Лаборатория Знаний, 2009. - 384с.

2. Угринович Н.Д. Информатика и ИКТ: учебник для 8 класса - М.: БИНОМ. Лаборатория Знаний, 2009. - 185с.

Использованные материалы и Интернет-ресурсы

1. im4.asset.yvimg.kz/userimages/v_shal/D7QjaCk78OpAS3taCtq3yjg86L7HPj.jpg

2. festival.1september.ru/articles/514293/img1.jpg

3. www.klyaksa.net/htm/kopilka/uchp/images/p49.jpg</

4. 900igr.net/datas/matematika/Primery-sistem-schislenija/0008-008-Slavjanskaja-sistema-schislenija.jpg