- Учителю
- Основы логики для подготовки к ЕГЭ
Основы логики для подготовки к ЕГЭ
-
Тема: «Основы логики при подготовке учащихся к ЕГЭ по информатике»
Оглавление
Введение 3
Глава 1. Теоретический анализ раздела «Основы логики» 5
1.1. Формы мышления. Алгебра высказываний. 5
1.2. Логические выражения и функции 8
1.3. Логические законы 9
1.4. Базовые логические элементы 11
Глава 2. Методика подготовки к ЕГЭ по теме «Основы логики» 15
2.1. Кодификатор 15
2.2. Разбор заданий 16
2.3. Основные трудности при решении заданий 20
2.4. Анализ выполнения заданий этой темы 25
Глава 3. Решения задач ЕГЭ по теме «Основы логики» 27
Заключение 33
Список литературы 34
Введение
Подготовка к ЕГЭ по информатике стала актуальной с введением экзамена по информатике по выбору при окончании средней школы и введением в некоторых ВУЗах, включая и гуманитарные, вступительных экзаменов по информатике.
Тема «Логика. Логические основы компьютера» - один из разделов, изучаемых в рамках учебной дисциплины «Информатика и ИКТ» на профильном уровне. В силу своей предельной общности и абстрактности логика имеет отношение буквально ко всем конкретным отраслям науки и техники. Потому, что как бы ни были различны и своеобразны эти отрасли, все же законы и правила мышления, на которых они основываются, едины.
Изучение логики развивает: ясность и четкость мышления; способность предельно уточнять предмет мысли; внимательность, аккуратность, обстоятельность, убедительность в суждениях; умение абстрагироваться от конкретного содержания и сосредоточиться на структуре своей мысли.
Предмет исследования - методы подготовки к ЕГЭ по информатике по теме «Основы логики».
Объект исследования - раздел «Основы логики» школьного курса информатики.
Цель: комплексное, системное изучение методики подготовки к ЕГЭ по информатике по теме «Основы логики».
Достижение поставленной цели требует постановки и решения следующих задач:
-
провести теоретический анализ раздела «Основы логики»;
-
рассмотреть возможные трудности при решении задач данной темы.
Глава 1. Теоретический анализ раздела «Основы логики»
1.1. Формы мышления. Алгебра высказываний.
Логика - наука о способах и формах мышления, которая возникла в Древнем Китае и Индии.
Основоположником формальной логики по праву считается Аристотель. Логика позволяет, отвлекаясь от содержательной стороны, строить формальные модели окружающего мира. Свойства, связи, и отношения объектов окружающего мира в сознании человека отражают законы логики.
Мышление всегда осуществляется в следующих формах: понятие, высказывание и умозаключение.
Алгебра высказываний позволяет определять истинность или ложность составных высказываний.
В алгебре высказываний простым высказываниям или суждениям соответствуют логические переменные. Истинному высказыванию соответствует значение логической переменной 1, а ложному - значение 0. Над высказываниями можно производить определенные логические операции, в результате которых получаются новые, составные высказывания[14, 98 c.].
Для образования новых высказываний наиболее часто используются базовые логические операции, выражаемые с помощью логических связок «и» (логическое умножение (конъюнкция)), «или» (логическое сложение (дизъюнкция)), «не» (логическое отрицание (инверсия)).
Конъюнкция. Операцию логического умножения (конъюнкцию) принято обозначать значком «&» либо «/\»:
F = А /\ В.
Функция логического умножения F может принимать лишь два значения «истина» (1) и «ложь» (0). Значение логической функции определяется с помощью таблицы истинности:
0
0
0
1
0
1
0
0
1
1
1
Дизъюнкция. Операцию логического сложения обозначают «v» либо «+».
F = A\/B
Таблица истинности:
0
0
0
1
1
1
0
1
1
1
1
Инверсия. Операцию логического отрицания обозначают F = ¬A.
Таблица истинности логического отрицания:
1
1
0
Равносильными логическими выражениями называются логические выражения, у которых совпадают последние столбцы таблиц истинности.
Логическое следование (импликация) - это логическая функция, которую можно описать помощью оборота «если..., то...», и обозначается:
А -> В.
Таблица истинности:
0
1
0
1
1
1
0
0
1
1
1
Логическое равенство (эквивалентность) - это логическая функция, которую можно описать помощью оборота «тогда и только тогда, когда ...» и обозначается А<->В.
Таблица истинности:
1
0
1
0
1
0
0
1
1
1
1.2. Логические выражения и функции
Логические выражения. Составные высказывания можно представить в виде логического выражения или формулы, которая состоит из логических переменных, обозначающих высказывания, и знаков логических операций.
Логические операции выполняются в следующем порядке: инверсия, конъюнкция, дизъюнкция. Скобки позволяют этот порядок изменить:
F = (A\/B) /\ (A\/B)
Таблицу истинности можно построить для каждого логического выражения. Она определяет его значение при всех возможных комбинациях значений логических переменных [14, 99 c.].
Построение таблицы истинности:
-
Количество строк N в таблице истинности равно количеству возможных комбинаций значений логических переменных n и определяется по формуле: N = 2n.
-
Количество столбцов в таблице истинности равно количеству логических переменных плюс количество логических операций.
-
Построить таблицу истинности с необходимым количеством строк и столбцов и записать значения исходных логических переменных.
-
Заполнить таблицу истинности по столбцам, в соответствии с таблицами истинности.
1.3. Логические законы
Закон тождества. Всякое высказывание тождественно самому себе:
А = А.
Закон непротиворечия. Высказывание не может быть одновременно истинным и ложным:
А /\ ¬А = 0.
Закон исключенного третьего. Высказывание может быть либо истинным, либо ложным:
A \/ ¬A = 1.
Закон двойного отрицания. Двойное отрицание дает в итоге исходное высказывание:
¬¬А = А
Законы де Моргана:
¬(A \/ B) = ¬A /\ ¬B
¬(A /\ B) = ¬A \/ ¬B
Закон коммутативности.
А /\ В = В /\ А
A \/ B = B \/ A
Закон ассоциативности:
(А /\ В) /\ С = А /\ (В /\ С)
(A \/ B) \/ C = A \/ (B \/ C)
Закон дистрибутивности. Отличается от подобного закона в алгебре - за скобки можно выносить не только общие множители, но и общие слагаемые:
(A /\ B) \/ (A /\ C)=A /\ (B \/ C)
(A \/ B) /\ (A \/ C) = A \/ (B /\ C)
1.4. Базовые логические элементы
В основе обработки компьютером информации лежит алгебра логики, разработанная английским математиком Дж. Булем. Схемные реализации логических операций называются логическими элементами.
Логический элемент НЕ преобразует сигнал в противоположный, например, если на вход элемента подана логическая единица, то на выходе этого элемента будет логический ноль и наоборот.X
НЕ
НЕ X
0
1
1
0
Л
ИЛИогический элемент ИЛИ преобразует два сигнала,
поданных на вход, в один сигнал на выходе по следующему принципу.
Если на любой вход логического элемента ИЛИ будет подана логическая
единица, то на выходе элемента будет логическая единица. Если на
оба входа подан логический ноль, то на выходе элемента ИЛИ также
будет ноль. 0
0
0
0
1
1
1
0
1
1
1
1
Л
Иогический элемент И преобразует два сигнала,
поданных на вход, в один сигнал на выходе по следующему принципу.
Если на любой вход логического элемента И будет подана логическая
единица, а на другой вход логический ноль, то на выходе элемента
будет логический ноль. Если на оба входа подана логическая единица,
то на выходе элемента И также будет единица. 0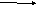
0
0
0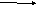
1
0
1
0
0
1
1
1
Из тысяч и миллионов таких элементов строится ЭВМ [14, 103 c.].
Рассмотрим, как из логических элементов можно сконструировать устройство для сложения двух двоичных чисел - так называемый одноразрядный сумматор или полусумматор. Это устройство должно давать на выходе следующие сигналы:
0 + 0 = 00
0 + 1 = 01
1 + 0 = 01
1 + 1 = 10
Многоразрядный сумматор состоит из полных одноразрядных сумматоров, соединенных следующим образом: на каждый разряд ставится одноразрядный сумматор, причем выход (перенос) сумматора младшего разряда подключается ко входу сумматора старшего разряда.
Глава 2. Методика подготовки к ЕГЭ по теме «Основы логики»
2.1. Кодификатор
11.5
Логика и алгоритмы
1
1.5.1
Высказывания, логические операции, кванторы, истинность высказывания
3
3.5.2
Использование инструментов поисковых систем (формирование запросов)
Материал, проверяемый ЕГЭ
На уровне воспроизведения знаний проверяется такой фундаментальный теоретический материал, как: основные элементы математической логики.
Материал на проверку сформированности умений применять свои знания в стандартной ситуации:
-
создавать и преобразовывать логические выражения;
-
формировать для логической функции таблицу истинности и логическую схему.
Материал на проверку сформированности умений применять свои знания в новой ситуации: решать логические задачи.
2.2. Разбор заданий
По теме «Основы логики» в экзаменационной работе содержалось четыре задания: два с выбором ответа и два с кратким ответом. Эти задания включали в себя проверку умения строить таблицы истинности и логические схемы, преобразовывать логические выражения, решение логического уравнения. Уровень сложности, максимальный первичный балл и время выполнения определяется по спецификации. Обозначения: Б - базовый уровень сложности, П - повышенный уровень сложности, В - высокий уровень сложности.Коды
требований к уровню
подготовки
выпускников по кодификато
ру
Коды видов деятельности (п.5 спецификации)
Уровень сложности задания
Макс. балл за выполнение задания
Примерное время выполнения задания (мин.)
А3
Умения строить таблицы
истинности и логические схемы
1.5.1
1.1.6
2
Б
1
2
А10
Знание основных понятий и
законов математической логики
1.5.1
1.1.7
2
П
1
2
В12
Умение осуществлять поиск информации в Интернет
3.5.2
2.1
3
П
1
2
В15
Умение строить и преобразовывать логические выражения
1.5.1
1.1.7
3
В
1
10
В экзаменационных заданиях используются следующие соглашения:
1. Обозначения для логических связок (операций):
-
отрицание (инверсия) обозначается ¬ (например, ¬А);
-
конъюнкция (логическое умножение, логическое И) обозначается /\ (например, А /\ В);
-
дизъюнкция (логическое сложение, логическое ИЛИ) обозначается \/ (например, A \/ В);
-
следование (импликация) обозначается -> (например, А -> В);
-
символ 1 используется для обозначения истины (истинного высказывания); символ 0 - для обозначения лжи (ложного высказывания).
2. Два логических выражения, содержащих переменные, называются равносильными (эквивалентными), если значения этих выражений совпадают при любых значениях переменных. Так, выражения А -> В и (¬А) \/ В равносильны, а А \/ В и А /\ В - нет (значения выражений разные, например, при А = 1, В = 0).
3. Приоритеты логических операций: инверсия (отрицание), конъюнкция (логическое умножение), дизъюнкция (логическое сложение), импликация (следование), эквивалентность (равносильность). Таким образом, ¬А /\ В \/ С /\ D совпадает с ((¬А) /\ В) \/ (С /\ D). Возможна запись А /\ В /\ С вместо (А /\ В) /\ С. То же относится и к дизъюнкции: возможна запись А \/ В \/ С вместо (А \/ В) \/ С.
2.3. Основные трудности при решении заданий
Задание А10 повышенного уровня на проверку знания основных понятий и законов математической логики. Задание А3 базового уровня на умение строить таблицы истинности и логические схемы, задания В12, повышенного уровня, проверяют умение осуществлять поиск информации в Интернет, используя логические операции. Задание В15 относится к высокому уровню сложности, требует от экзаменуемого умения строить и преобразовывать логические выражения.
А3. Умение строить таблицы истинности и логические схемы.
Типичные ошибки:
-
серьезные сложности представляет применяемая в заданиях ЕГЭ форма записи логических выражений с «закорючками», поэтому рекомендуется сначала внимательно перевести их в «удобоваримый» вид;
-
расчет на то, что ученик перепутает значки и (неверный ответ 1);
-
в некоторых случаях заданные выражения-ответы лучше сначала упростить, особенно если они содержат импликацию или инверсию сложных выражений.
А10. Знание основных понятий и законов математической логики.
Типичные ошибки:
-
можно «забыть» отрицание (помните, что правильный ответ - всего один!);
-
можно перепутать порядок операций (скобки, «НЕ», «И», «ИЛИ», «импликация»);
-
нужно помнить таблицу истинности операции «импликация»;
-
нужно помнить законы логики (например, формулы де Моргана);
-
при использовании формул де Моргана нужно не забыть заменить «И» на «ИЛИ» и наоборот;
-
нужно не забыть, например, что инверсией (отрицанием) для выражения X > 3 является X ≤ 3, а не X < 3;
-
иногда для решения нужно упростить не только исходное выражение, но и заданные ответы, если они содержат импликацию или инверсию сложных выражений.
В12. Умение осуществлять поиск информации в Интернет.
Типичные ошибки:
-
нужно внимательно читать условие, так как в некоторых задачах требуется перечислить запросы в порядке убывания количества результатов, а в некоторых - в порядке возрастания;
-
можно ошибиться в непривычных значках: «И» = &, «ИЛИ» = | (эти обозначения привычны для тех, кто программирует на языке Си);
-
можно перепутать значение операций «И» и «ИЛИ», а также порядок выполнения цепочки операций (сначала - «И», потом - «ИЛИ»);
-
для сложных запросов не всегда удастся так просто расположить запросы по возрастанию (или убыванию) ограничений;
-
решение достаточно громоздко, хотя позволяет с помощью простых операций решить задачу, не рискуя ошибиться при вычислениях «в уме» в сложных случаях;
-
внимательнее с индексами переменных, очень легко по невнимательности написать, например, N5 вместо N6 и получить совершенно другой результат.
В15. Умение строить и преобразовывать логические выражения.
Типичные ошибки:
-
Плохое знание таблиц истинности;
-
Ошибки из-за невнимательности к значкам, которыми в выражениях обозначают логические операции. Это происходит от того, что в разных учебниках эти значки отличаются по написанию;
-
нужно помнить правила преобразования логических выражений и хорошо владеть этой техникой;
-
легко запутаться в многочисленных столбцах с однородными данными (нулями и единицами);
-
длинное запутанное условие, из которого нужно выделить действительно существенную информацию и формализовать ее;
-
легко по невнимательности перепутать порядок букв в ответе.
2.4. Анализ выполнения заданий этой темы
По разделу «Основы логики» в экзаменационной работе содержится четыре задания: два с выбором ответа и два с кратким ответом. Одно задание базового, два повышенного и одно - высокого уровня сложности. Экзаменуемые хорошо справились с заданием А3 базового уровня на проверку умения строить таблицы истинности и логические схемы: 79% выполнения в среднем. Результат практически эквивалентен предыдущим годам. Результат выполнения задания А10 повышенного уровня на проверку знания основных понятий и законов математической логики также выше результатов прошлых лет: 74% [2, 90 c.].
Как и в прошлые годы задание В12 повышенного уровня сложности на умение осуществлять поиск информации в Интернете с использованием логических операций дало результат в среднем 51%. Результат выполнения задания В15 высокого уровня сложности с кратким ответом на умение строить и преобразовывать логические выражения составил 69%.
В целом в 2013 году по теме «Основы логики» результаты полностью соответствуют и иногда даже превосходят результаты, прогнозировавшиеся комиссией. Можно сделать окончательный вывод о том, что повышенное внимание, уделенное этому разделу при разборе результатов ЕГЭ предыдущих лет, дало свои плоды: результат усвоения этой темы не выбивается из общего ряда.
Глава 3. Решения задач ЕГЭ по теме «Основы логики»
А3. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F:
Какое выражение соответствует F?
1) ¬X ¬Y ¬Z 2) X Y Z 3) X ¬Y ¬Z 4) X ¬Y ¬Z
Решение:
-
перепишем ответы в других обозначениях: 1)
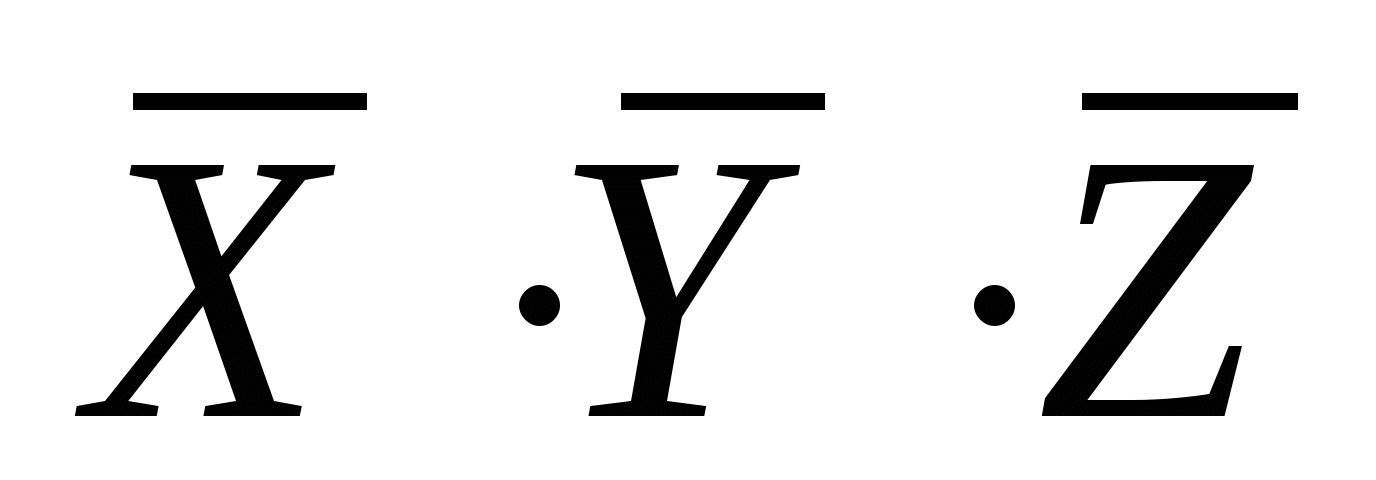 2)
2) 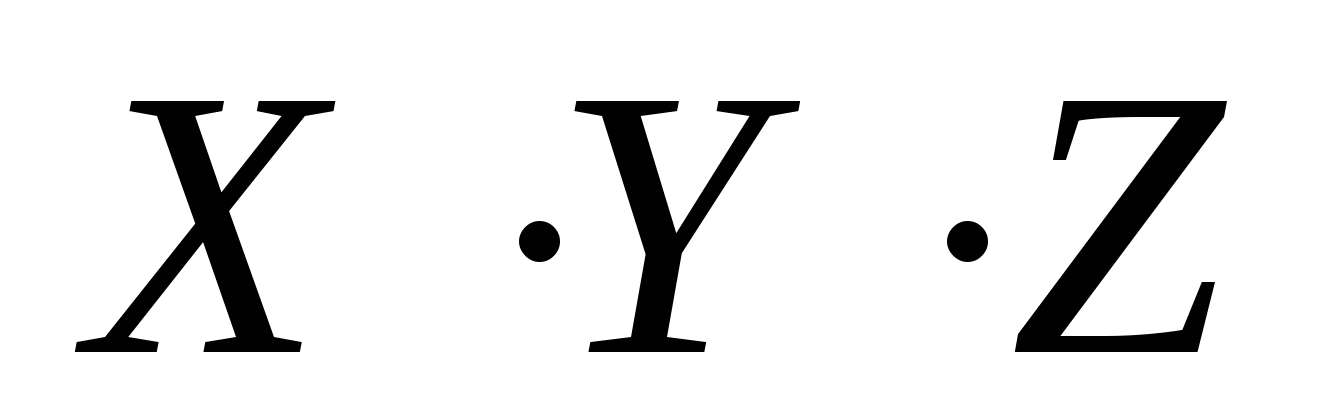 3)
3) 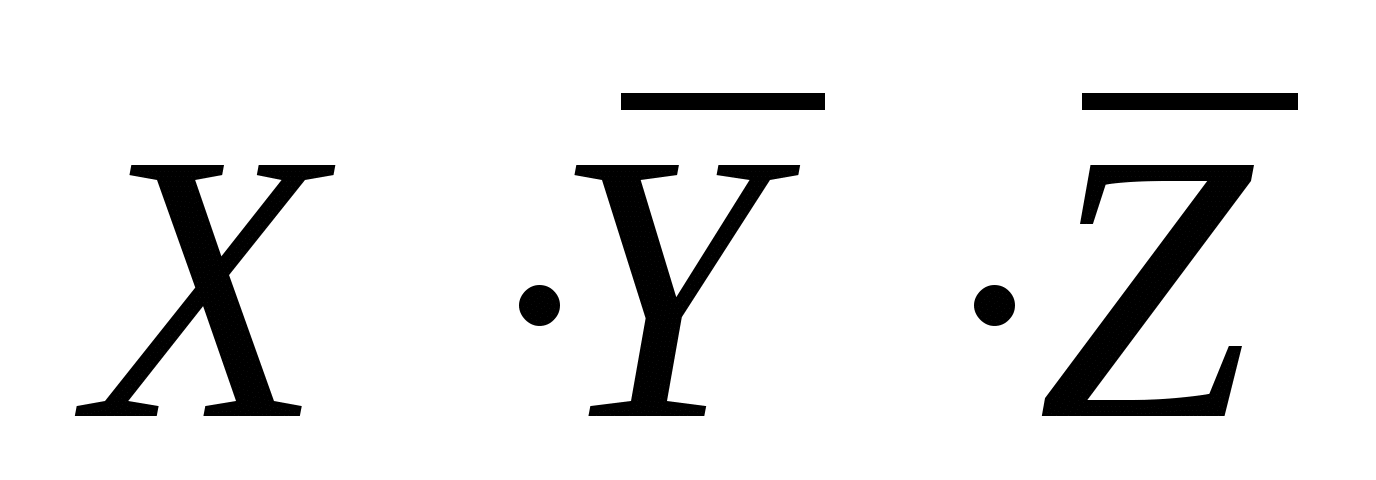 4)
4) 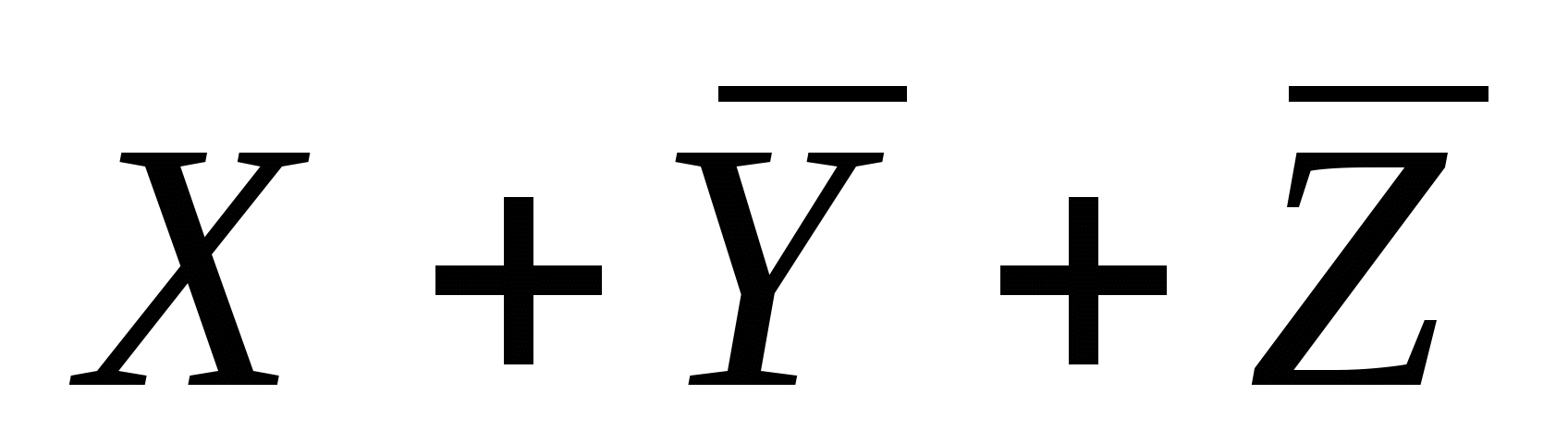
-
в столбце F есть единственная единица для комбинации
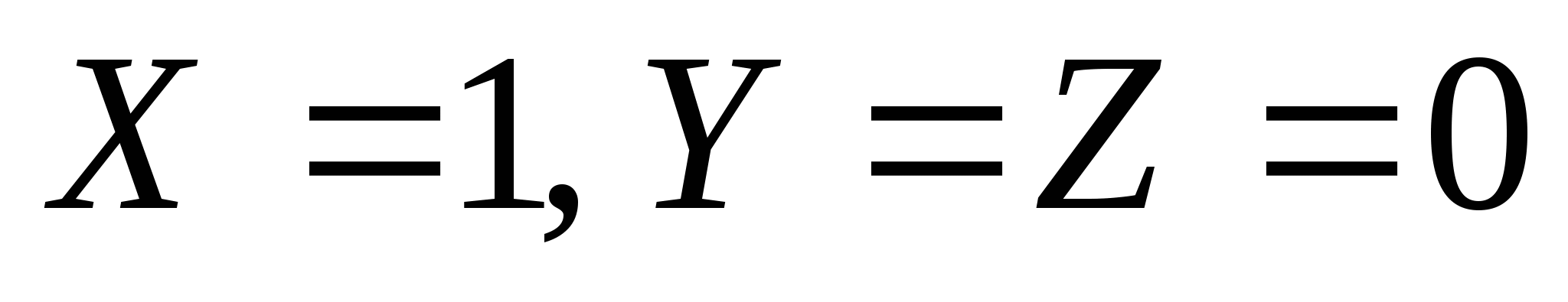 , простейшая
функция, истинная (только) для этого случая, имеет вид
, простейшая
функция, истинная (только) для этого случая, имеет вид
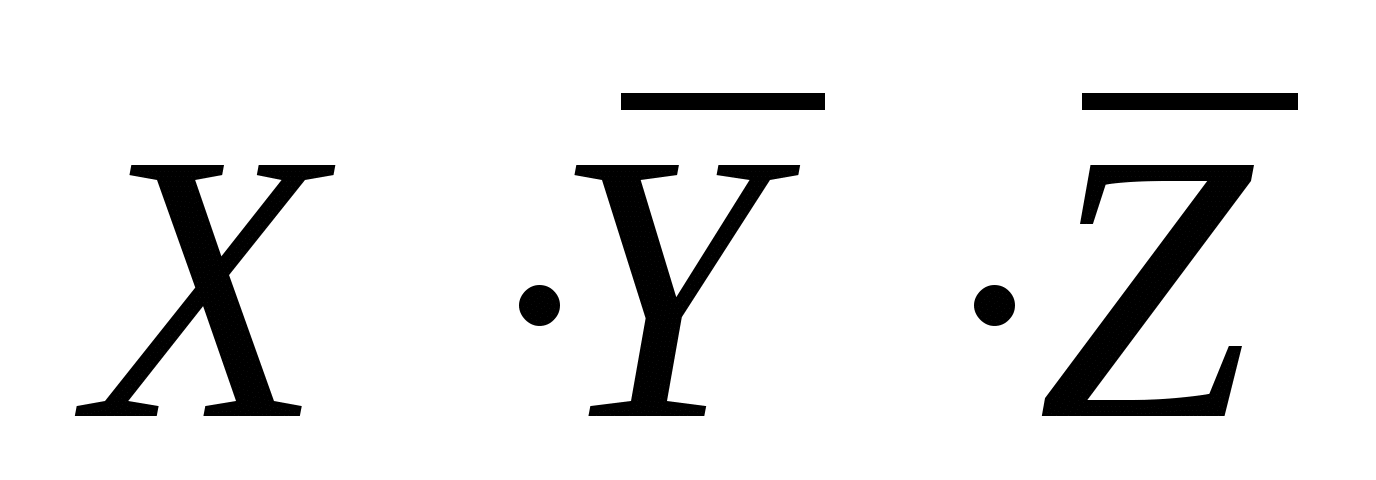 , она есть среди
приведенных ответов (ответ 3)
, она есть среди
приведенных ответов (ответ 3)
-
таким образом, правильный ответ - 3.
А 10. На числовой прямой даны два отрезка: P =[10?30] и Q=[25,55]. Определите наибольшую возможную длину отрезка A, при котором формула (xA)→((xP) (xQ)) тождественна истинна, то есть принимает значение 1 при любом значении переменной x.
-
10 2) 20 3) 30 4) 45
Решение:
-
для того, чтобы упростить понимание выражения, обозначим отдельные высказывания буквами
A: x А, P: x P, Q: x Q
-
перейдем к более простым обозначениям
A → (P + Q)
-
раскроем импликацию через операции НЕ и ИЛИ (
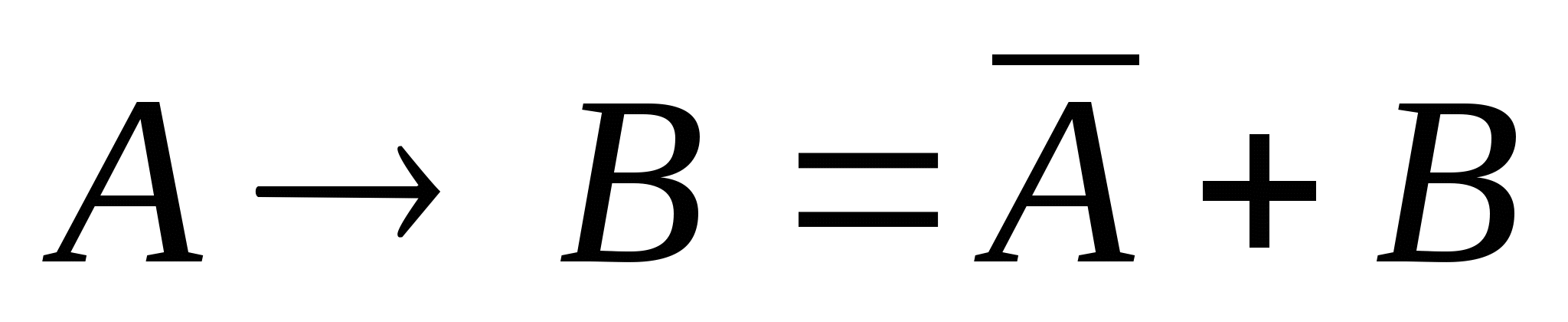 ):
):
![]()
-
для того, чтобы выражение было истинно при всех x, нужно, чтобы
 было
истинно там, где ложно
было
истинно там, где ложно 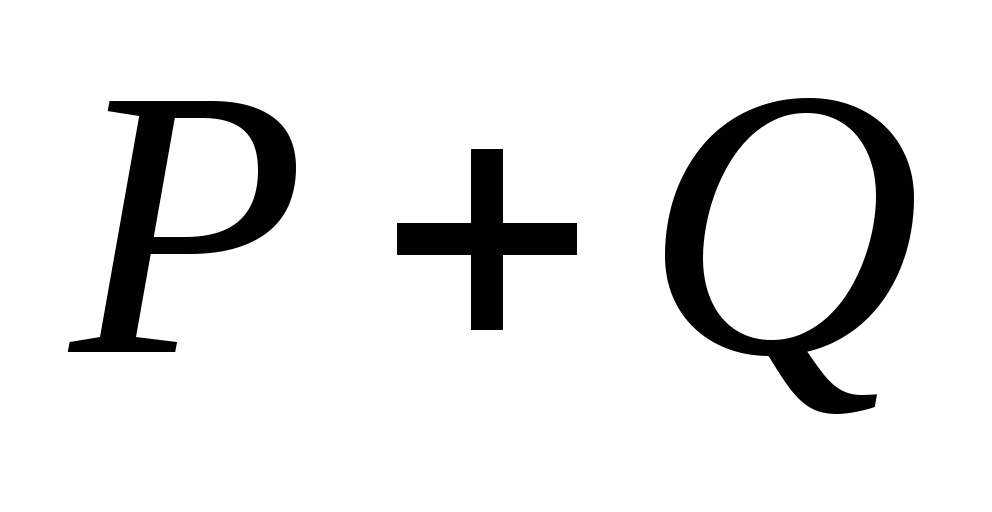 (жёлтая область на рисунке)
(жёлтая область на рисунке)
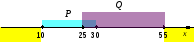
-
поэтому максимальный отрезок, где A может быть истинно (и, соответственно,
 ложно) - это отрезок
[10,55], имеющий длину 45
ложно) - это отрезок
[10,55], имеющий длину 45
-
Ответ: 4.
В12. В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
-
Сколько страниц (в тысячах) будет найдено по запросу Рубин &
Динамо & Спартак?
Решение (вариант 1, круги Эйлера, полная диаграмма):
-
в этой задаче неполные данные, так как они не позволяют определить размеры всех областей; однако их хватает для того, чтобы ответить на поставленный вопрос
-
обозначим области, которые соответствуют каждому запросу
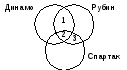
-
из таблицы следует, что в суммарный результат первых двух
запросов область 2 входит дважды (1 + 2 + 2 + 3), поэтому,
сравнивая этот результат с третьим запросом (1 + 2 + 3),
сразу находим результат четвертого:
N2 = (320 + 280) - 430 = 170
-
таким образом, ответ - 170.
В 15. Сколько различных решений имеет система логических уравнений
(x1x2) (x3x4)=1
(x3x4) (x5x6)=1
Где x1, x2,…,x6 - логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.
Решение (метод замены переменных):
-
используем замену переменных (заметим, что каждая из новых переменных независима от других, это важно!):
Y1 = x1 x2, Y2 = x3 x4, Y3 = x5 x6
тогда система запишется в виде
Y1 Y2 = 1
Y2 Y3 = 1
-
можно объединить эти уравнения в одно
(Y1 Y2) (Y2 Y3) = 1
для того, чтобы это равенство было выполнено, ни одно из импликаций не должна быть ложной, то есть в битовой цепочке, составленной из значений переменных Y1, Y2, Y3, не должно быть последовательности «10»; вот все возможные варианты:
-
теперь вернемся к исходным переменным; импликация
x1 x2 дает 0 при одном наборе
исходных переменных (x1,x2) =
(1,0) и 1 при трёх наборах
(x1,x2) = {(0,0), (0,1), (1,1)}
учитывая, что каждая из новых переменных Y1, Y2, Y3, независима от других; для каждой строки полученной таблицы просто перемножаем количество вариантов комбинация исходных переменных:складываем все результаты: 1 + 3 + 9 + 27 = 40
Ответ: 40.
Заключение
Тема «Логика. Логические основы компьютера» - один из разделов, изучаемых в рамках учебной дисциплины «Информатика и ИКТ» на профильном уровне.
Изучение логики развивает: ясность и четкость мышления; способность предельно уточнять предмет мысли; внимательность, аккуратность, обстоятельность, убедительность в суждениях; умение абстрагироваться от конкретного содержания и сосредоточиться на структуре своей мысли.
Важна роль задач в изучении этого раздела. Ученики должны понимать, что логика в силу своей предельной общности и абстрактности имеет отношение буквально ко всем конкретным отраслям науки и техники.
В работе представлены решения задач по теме «Основы логики», взятые из демо-версий ЕГЭ по информатике разных лет.
Таким образом, в результате проделанной работы были достигнута цель и решены поставленные задачи.
</ Список литературы
-
Бочкин А. И. Методика преподавания информатики. - Минск: Высшая школа, 2007. - 431 с.
-
ЕГЭ 2013. Информатика. Федеральный банк экзаменационных материалов / Авт.-сост. П. А. Якушкин, С. С. Крылов. - М. : Эксмо, 2013. - 160 с.
-
Информатика : ЕГЭ-2013 : Самые новые задания/авт.-сост. О.В. Ярцева, Е.Н. Цикина. - М.: ACT: Астрель, 2013. - 126 с.
-
Информатика и ИКТ: Учебник. Начальный уровень / Под ред. Н. В. Макаровой. - СПб.: Питер, 2011.
-
Информатика и ИКТ: Учебник. 8-9 класс / Под ред. Н. В. Макаровой. - СПб.: Питер, 2011.
-
Информатика и ИКТ: Практикум. 8-9 класс. / Под ред. Н. В. Макаровой. - СПб.: Питер, 2011.
-
Информатика и ИКТ: Учебник. 10 класс. Базовый уровень / Под ред. Н. В. Макаровой. - СПб.: Питер, 2011.
-
Информатика и ИКТ: Учебник. 11 класс. Базовый уровень / Под ред. Н. В. Макаровой - СПб.: Питер, 2011.
-
Информатика и ИКТ: Методическое пособие для учителей. Т. 1. / Под ред. проф. Н. В. Макаровой. - СПб.: Питер, 2011.
-
Информатика и ИКТ: Методическое пособие для учителей. Т. 2. / Под ред. проф. Н. В. Макаровой. СПб.: Питер, 2011.
-
Информатика и ИКТ: Методическое пособие для учителей. Т. 3. / Под ред. проф. Н. В. Макаровой. СПб.: Питер, 2011.
-
Лапчик М. П. и др. Методика преподавания информатики. - М.: Академия, 2011. - 624 с.
-
Лыскова В. Ю., Ракитина Е. А. Логика в информатике. - М.: ЛБЗ, 2011. - 160 с.
-
Молодцов В.А. Информатика : тесты, задания, лучшие методики / Молодцов В.А., Рыжикова Н.Б. - Ростов н/Д : Феникс, 2008. - 217 с.
-
Подготовка к ЕГЭ по дисциплине «Информатика и ИКТ» / Под ред. Н. В. Макаровой. - СПб.: Питер, 2011.
-
Семакин И. Г., Шеина Т. Ю. Преподавание базового курса информатики в средней школе. Методическое пособие. - М.: БИНОМ. ЛБЗ, 2012.
-
Софронова Н. В. Теория и методика обучения информатике. - М.: Высшая школа, 2009. - 223 с.
29
-
-
-