Конспект урока на тему Модели на графах

Аннотация

Шашкова Юлия Николаевна, преподаватель информатики ГАПОУ ЧО «Политехнический колледж». Методическая разработка занятия на тему: «Информационные модели на графах»

В данной разработке представлен подробный план-конспект комбинированного занятия по дисциплине ЕН.02 «Компьютерное моделирование» для обучающихся по специальности 220703 «Автоматизация технологических процессов и производств» (по отраслям).

ТЕМА: №27-28 «Информационные модели на графах»

ДИСЦИПЛИНА: ЕН.02 Компьютерное моделирование

ФОРМА ПРОВЕДЕНИЯ: урок

ТИП: Комбинированный (смешанный)

ЦЕЛИ

1. Обучающая:

• Получение знаний о графах, их видах, свойствах;

• Отработка навыков преобразования весовой матрицы (табличной формы представления информации) в граф;

• Формирование навыков построения путей в графе и поиска кратчайшего пути.

2. Воспитательная:

• Воспитание добросовестного отношения к труду и к результатам своей деятельности;

• Воспитание дисциплинированности и организованности при выполнении работы.

3. Развивающая:

• Развитие умений учебного труда: работать в хорошем темпе;

• Развитие воли и самостоятельности: развитие инициативы, уверенности в своих силах, умения преодолевать трудности, развитие умения действовать самостоятельно.

ОК, частично формируемые на данном занятии:

ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.

ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития.

ОК 8. Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации.

ОБОРУДОВАНИЕ К УРОКУ: Персональный компьютер, мультимедийный проектор, экран, доска, мультимедийная презентация, дидактический материал.

ХОД УРОКАРебята, добрый день, приготовьте рабочие тетради.

Дежурный, кто сегодня отсутствует?

Слушают, отвечают.

2. Мотивация учебной деятельности (7-10 минут)

Давайте вспомним, какие виды моделей мы уже изучили на предыдущих занятиях?

Мы с вами сегодня будем изучать еще один вид информационных моделей - информационные модели на графах.

Записываем тему занятия в тетрадь: «Информационные модели на графах»

На занятии мы познакомимся с графами, узнаем для чего они нужны, какие виды существуют и как их можно использовать для решения ряда задач (например, из ЕГЭ)

Графы используются во многих областях практической и научной деятельности людей.

Теория графов находит применение, например, в геоинформационных системах (ГИС). Существующие или вновь проектируемые дома, сооружения, кварталы и т. п. рассматриваются как вершины, а соединяющие их дороги, инженерные сети, линии электропередачи и т. п. - как рёбра. Применение различных вычислений, производимых на таком графе, позволяет, например, найти кратчайший объездной путь или ближайший продуктовый магазин, спланировать оптимальный маршрут.

Определение планарности графа играет крайне важную роль в промышленности. В электротехнике необходимо уметь реализовать ту или иную модель максимально простым способом, т.к. с ростом сложности возрастают и затраты на изготовлением модели. В частности, после того как определена модели цепи, которую необходимо реализовать, следует установить, можно ли представить эту цепь на плоской печатной плате. Если реализовать цепь на плоскости без самопересечений невозможно, то стоимость изготовления платы возрастет, т.к. она будет содержать не один, а несколько слоев. Учитывая, что объемы производства плат составляют миллионы экземпляров, то изучение планарности электрических цепей играет решающую роль при оптимизации затрат. Существуют компьютерные программы, позволяющие определить, допускает ли заданная модель представления на плоскости, и оптимизировать конфигурацию соответствующей печатной платы

С помощью графов часто упрощается решение задач, сформулированных в различных областях знаний: в автоматике, электронике, физике, химии и др. Помогают графы в решении математических и экономических задач.

Отвечают: математические, словесные, структурные, иерархические модели

Слушают, записывают тему занятия в тетрадь

Смотрят презентацию с областью применения графов, записывают область применения в тетрадь

Перед вами на доске задача: в таблице представлено расстояние между населенными пунктами в километрах. Определить кратчайшее расстояние между пунктами A и E.

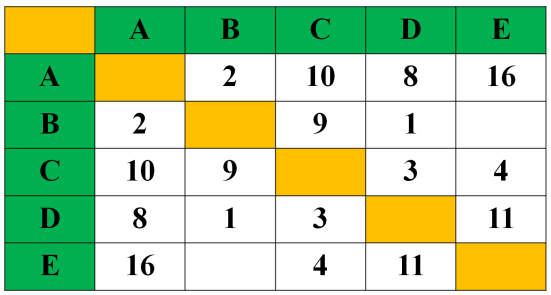
Давайте проанализируем ситуацию и определим препятствия, которые нам мешаю решить эту задачу сразу.

Обсуждение.

Оставим эту задачу и вернемся к ней чуть позже.

Пытаются решить задачу

Делают вывод: Очевидно, что форма представления информации в это задаче слишком неудобна для решения. Следовательно, можно предположить, что форму представления необходимо изменить, т.е. произвести кодирование информации.

Вспомним головоломку, известную вам как «Распечатанный конверт» или «Домик»

Предлагаю вам, не отрывая руки и не проводя дважды по одной и той же линии, начертить этот конверт. Даю вам на это 1 минуту. Те, у кого получилось, могут выйти к доске и показать маршрут, по которому они следовали.

В каких вершинах вы начали? А в каких закончили?

У кого не получилось? С каких вершин вы начинали?

Пробуют решить головоломку в тетради

Один-два выходят к доске и показывают свои варианты решения

Отвечают на вопросы, обсуждают результаты

3. Объяснение нового материала (30 минут)

Предлагаю вашему вниманию историческую головоломку (задачу)

Река Прегель, протекающая через Калининград (прежде город назывался Кенигсбергом) омывает два острова. Берега реки с островами были связаны мостами так, как это показано на рисунке.

Вопрос: можно ли составить маршрут экскурсии по мостам, проходящий по всем четырем участкам суши по одному разу, а конец и начало пути должны совпадать (т.е. вернуться в исходную точку).

Обратимся на минутку к истории. В 1736 году великий математик Леонард Эйлер нашел решение головоломки, носящей название «Проблема кѐнигсбергских мостов».

Эйлер доказал, что маршрута, который бы отвечал условиям головоломки, не существует, и разработал теорию решения такого рода головоломок. Схема, приведенная на рисунке не является, строго говоря графом. Тем не менее, 1736 год, когда эта головоломка была решена, принято считать годом рождения теории графов.

Эйлер пришёл к следующим выводам:

• Число нечётных вершин (вершин, к которым ведёт нечётное число рёбер) графа должно быть чётно. Не может существовать граф, который имел бы нечётное число нечётных вершин.

• Если все вершины графа чётные, то можно, не отрывая карандаша от бумаги, начертить граф, при этом можно начинать с любой вершины графа и завершить его в той же вершине.

• Граф с более чем двумя нечётными вершинами невозможно начертить одним росчерком.

Граф кёнигсбергских мостов имел четыре (синим) нечётные вершины (то есть все), следовательно, невозможно пройти по всем мостам, не проходя ни по одному из них дважды.

Созданная Эйлером теория графов нашла очень широкое применение в транспортных и коммуникационных системах (например, для изучения самих систем, составления оптимальных маршрутов доставки грузов или маршрутизации данных в Интернете)

Перейдем к определениям темы.

Определение понятия «граф» и его структуры. Попробуем изобразить графически систему отношений между детьми: Маша дружит с Костей и Таней, Марина дружит с Таней и с Машей, Костя дружит с Таней и Сашей. Для того, чтобы представить информацию о составе и структуре системы графически, необходимо изобразить компоненты системы и соединить их между собой какими-либо линиями. Таким образом, мы с вами построили граф.

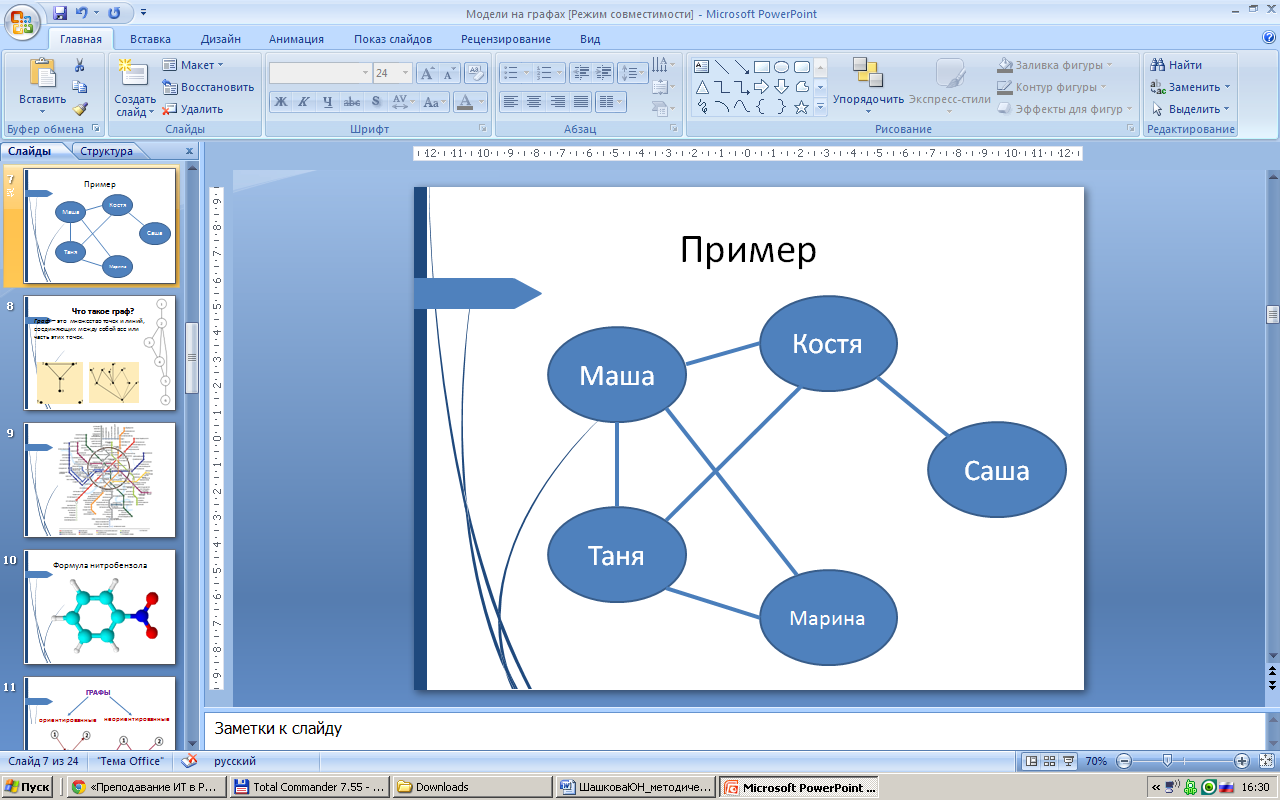
Слушают

Обучающиеся выполняют задания, но возникает трудность - не могут выполнить

Граф - это средство для наглядного представления состава и структуры системы. Перечислим элементы структуры графа:

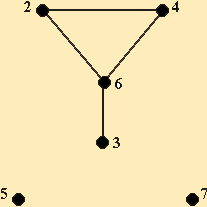
Граф состоит из вершин, связанных линиями.

Вершины графа изображаются кругами, овалами, прямоугольниками и пр.

Дуга - это направленные линии (стрелки), связывающие вершины (односторонняя связь).

Ребра - это ненаправленные линии, связывающие вершины (двусторонняя связь).

В графе различают: цепь и цикл.

Цепь - это путь по вершинам и ребрам (дугам) графа не более одного раза.

Например, Маша - Костя - Таня

Цикл - это цепь, у которой начальная и конечная вершины совпадают.

Например, Маша - Костя - Таня - Маша

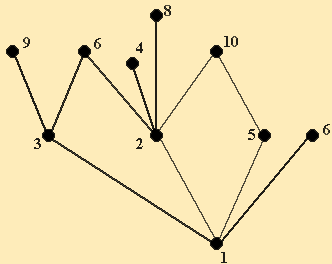
Рассмотрите примеры графов:

Записывают:

- определение;

- элементы графа

Типы графов.

Граф называется неориентированным, если его вершины соединены ребрами.

Граф называется ориентированным, если его вершины соединены дугами.

Граф называется взвешенным, если его вершины или рѐбра (дуги) характеризуются весом.

Записывают и зарисовывают типы графов в тетрадь

Вывод: Описать граф - это значит, ответить на вопросы:

• Сколько вершин?

• Есть ли рёбра?

• Есть ли направление?

• Все ли вершины соединены рёбрами?

Отвечают на вопросы

Вернемся к задаче, предложенной вам в начале занятия.

В таблице представлено расстояние между населенными пунктами в километрах. Определить кратчайшее расстояние между пунктами A и E.

Как преобразовать информацию, представленную в табличной форме в граф

Обратите внимание, части таблицы, разделённые диагональю - симметричны, т.е. содержат одни и те же данные. Следовательно, можно рассматривать данные любой половины таблицы, разделенной диагональю.

Как определить все пути в графе?

Определить кратчайший путь?

Смотрят на задание, записывают таблицу в тетрадь, строят по табличным данным граф, вычисляют вес, находят кратчайший путь от А к Е

Давайте разберем задачу с весовой матрицей и преобразование её в граф, вычислением расстояния на каждом пути и определение кратчайшего из них.

Алгоритм действия

1. Указываем вершины графа: А, В, С, Д, Е.

2. Соединяем вершины дугами (только те вершины, которые в таблицы имеют вес).

3. Указываем вес графа (над дугами).

4. Находим все возможные маршруты следования от А к Е.

5. Вычисляем сумму весов дуг каждого маршрута.

6. Делаем вывод - ответ на ключевой вопрос задачи.

Будем делать обход по графу в алфавитном порядке, т.е. сначала все пути через АВ, АС, AD и т.д.

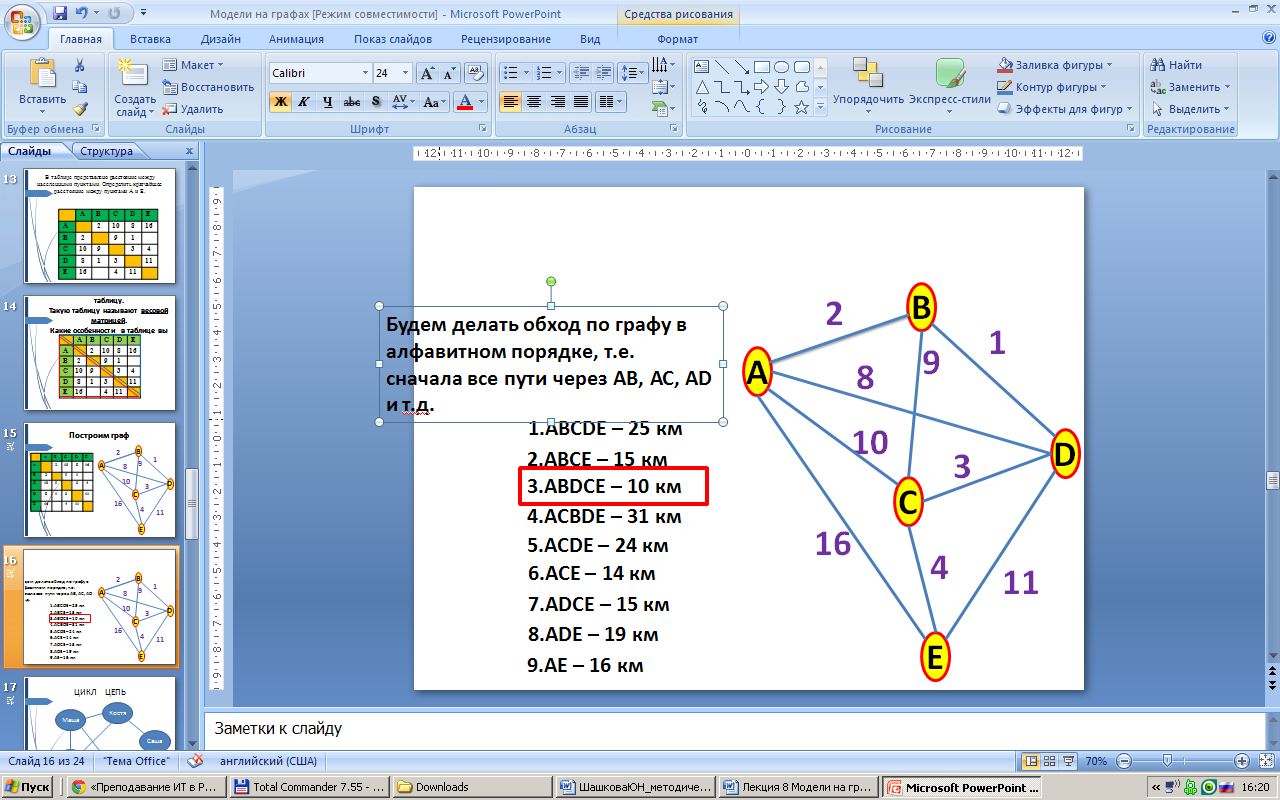
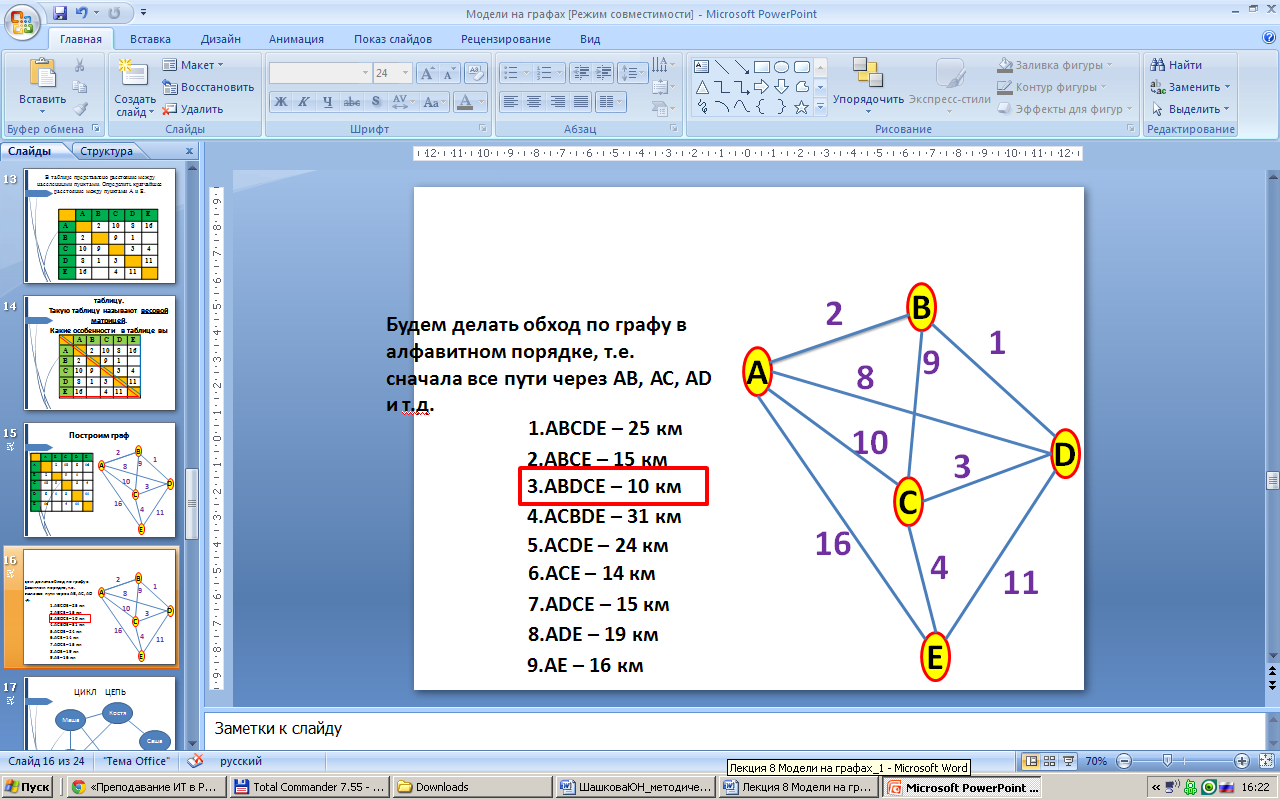
Граф с циклом называется сетью.

В искусственном интеллекте существует раздел, который называется компьютерная лингвистика. Задача этой науки - научить компьютер общаться с человеком на естественном языке. Смысл любой фразы зависит не только от слов, ее составляющих, но и от связей между словами. Классический пример: «Казнить, нельзя помиловать» или «Казнить нельзя, помиловать». Для того, чтобы выяснить смысл фразы, надо разобраться в ее структуре. А для этого удобно использовать графы.

Например, фразу «С утра на улице шел теплый грибной дождь» можно представить графом:

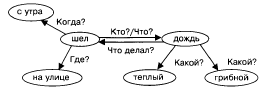
Если в вершинах этого графа заменить члены предложения на другие родственные слова, то снова может получиться осмысленная фраза. Даже фраза, не содержащая конкретных понятий, может нести определенный смысл. Например «Какой-то кто-то чем-то кого-то что-то». Здесь вообще нет никаких определенных объектов и понятий, но есть связи. В результате возникает некоторая картина событий. Подобные модели закладываются в компьютерную память и используются для анализа текстов на естественных языках.

Семантическая сеть - это граф, на котором отражены объекты (понятия) и связи (отношения) между ними.

Записывают определения, указывают область применения графов, смотрят как составлять семантическую сеть

На каких предметах вы встречались с графами, приведите примеры?

Отвечают на вопрос: русский язык, математика, физика

4. Закрепление полученных знаний (30 минут)

Задание 1. Представьте в виде графа связи в следующих предложениях:

1. Однажды в студеную зимнюю стужу я из лесу вышел (Н.Некрасов)

2. Отплякиваясь от сурых пляк, каждый хамсик шмыряет на глын по пять гнусиков (Г.Остер)

3. Мряка друсит пусики и на друську одного пусика тратит полдолготика (Г.Остер)

4. Глокая куздра штепо кудланула бокра и кудлачит мохрястенького бокренка (Л.Щерба)

5. Выстребаны обстряхнуться и дутой чернушенькой объятно хлюпнут по маргазам (А. и Б. Стругацкие)

Один у доски, остальные в тетрадях строят семантическую сеть

Задание 2. Рассмотрим задачи из демоверсии ЕГЭ 2014 года

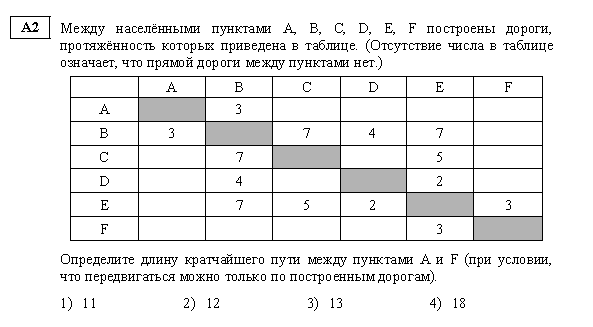
Алгоритм действия

1. Указываем вершины графа: А, В, С, Д, Е, F.

2. Соединяем вершины дугами (только те вершины, которые в таблицы имеют вес).

3. Указываем вес графа (над дугами).

4. Находим все возможные маршруты следования от А к F.

5. Вычисляем сумму весов дуг каждого маршрута.

6. Находим кратчайший путь.

Аналогично решается следующее задание

Один студент выполняет у доски, остальные в тетрадях.

Строят граф

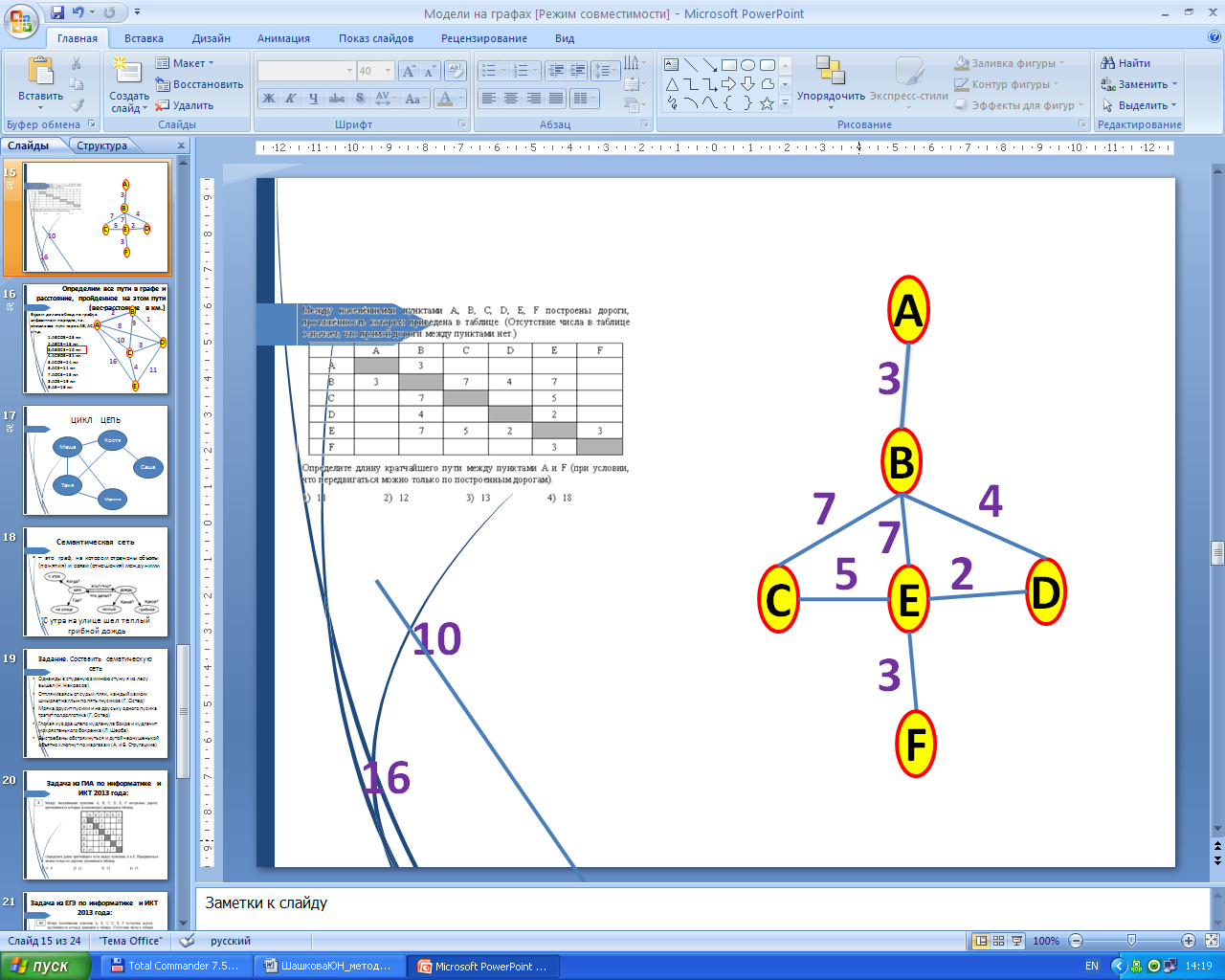
ABCEF=18

ABEF=13

ABDEF=12

ABCEBDF=31

Студенты самостоятельно решают, дают правильный ответ.

Задание 3. Демоверсия ГИА 2014 года. На рисунке - схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?

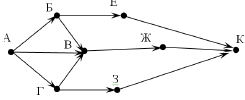
Алгоритм действия

1. Записываем все возможные маршруты следования от А к К, двигаться можно только по направлениям, указанным стрелками.

Один студент выполняет у доски, остальные в тетрадях.

Ответ:

АБЕК, АБВЖК, АВЖК, АГВЖК, АГЗК

5.Подведение итогов (5-7 минут)

Мы сегодня с вами изучили еще один вид информационных моделей, это информационным модели графах.

Оправдано ли использование графов?

Где вы еще встречаетесь с информационными моделями на графах?

Давайте повторим, что же это такое и для чего они нужны?

Вспомним, что такое граф.

Подведем итоги нашего занятия. Оценку получили….

Слушают, отвечают на вопросы

Можем классифицировать графы по типам: ориентированный, неориентированный, взвешенный

Можем на основе табличной информационной модели построить граф и определить все пути в нем

На основе анализа всех путей в графе мы можем делать заключение о том, какой путь самый короткий

6. Домашнее задание (5-7 минут)

1) Проработать конспект занятия, т.к. следующее занятие у нас начнется с маленькой проверочной работы (см.Приложение).

2) Решить задачу с помощью графов (задание раздается в печатном варианте)

В составе экспедиции должно быть 6 специалистов: биолог, врач, синоптик, гидролог, механик и радист. Имеется 8 кандидатов, из которых и нужно выбрать участников экспедиции; условные имена претендентов: A, B, C, D, E, F, G и H. Обязанности биолога могут исполнять E и G, врача - A и D, синоптика - F и G, гидролога - B и F, радиста - С и D, механика - C и H. Предусмотрено, что в экспедиции каждый из них будет выполнять только одну обязанность. Кого и в какой должности следует включить в состав экспедицию, если F не может ехать без B, D - без H и C, C не может ехать вместе с G, A - вместе с B?

Подсказка. Описать точный состав экспедиции, можно с помощью четного графа, в котором вершины разделены на две группы, а ребра могут соединять лишь вершины разных групп. Применительно к задаче об экспедиции одна группа вершин есть группа из 8 кандидатов, а вторая - из 6 должностей.

Читают задачу, слушают рекомендации по решению, задают уточняющие вопросы

Литература:

1. Мир математики в 45 т. Том 34: Хуанко Руэ. Искусство подсчета. Комбинаторика и перечисление/ Пер. с исп. - М.: Де Агостини, 2014. - 144с.

2. ГИА 2013 «Информатика». Каталог заданий. Задания B5. Анализирование информации, представленной в виде схем [текст]. URL: inf.sdamgia.ru/test?theme=11 (Дата обращения: 10.04.2014)

3. ЕГЭ 2013 «Информатика и ИКТ» [текст] URL: 4ege.ru/informatika/4175-demoversiya-ege-po-informatike-2014.html</<font face="Times New Roman, serif"> (Дата обращения: 10.04.2014)

Приложение

Задачи для самостоятельной работы

Вариант 1

1. Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)